浅谈高中立体几何的解题思路与技巧

张泓源

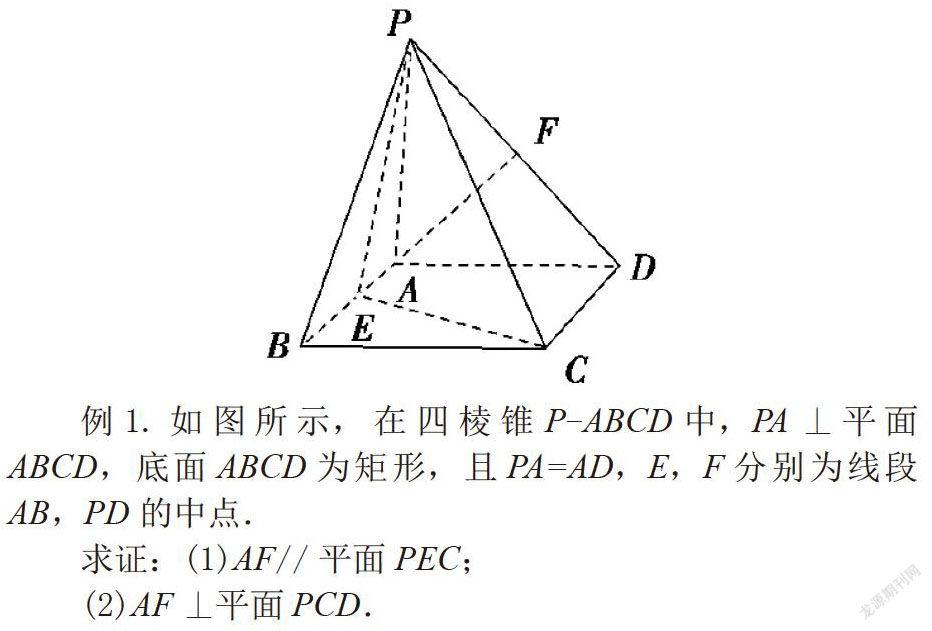
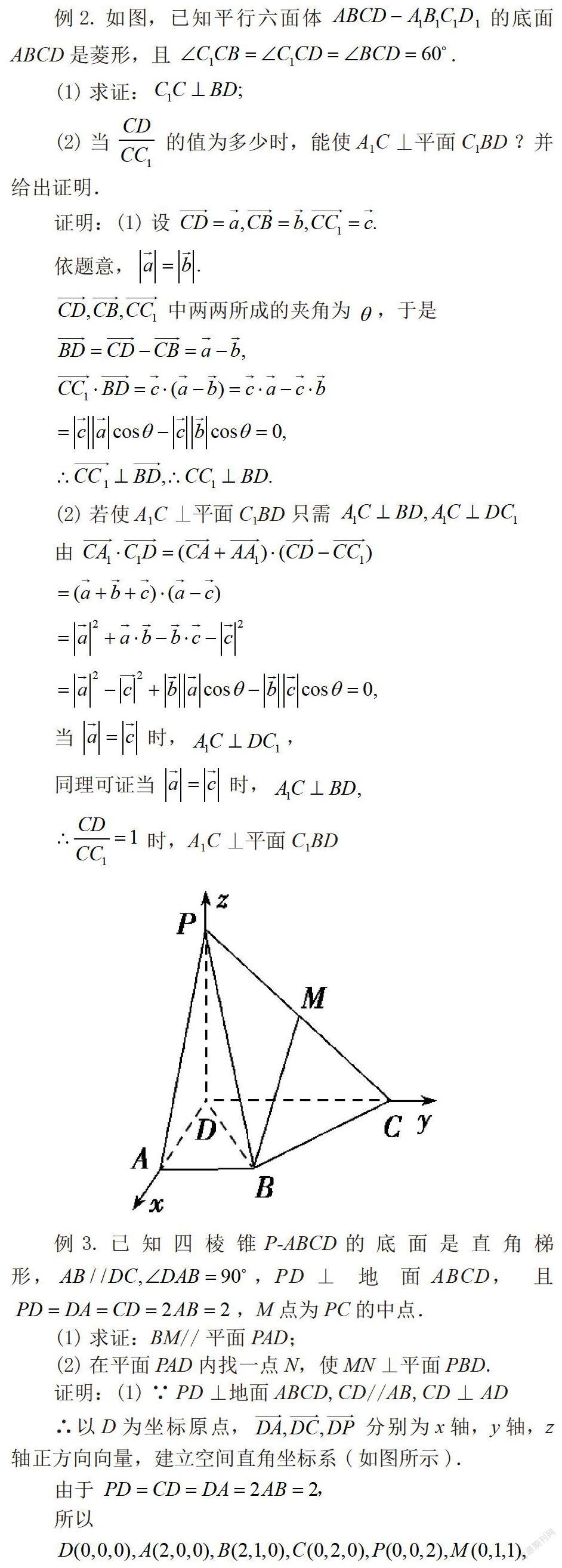
摘 要：随着知识的不断更新与教育的改革，在历年的高考中，立体几何所占的比值越来越重，应引起我们的高度重视。而对于立体几何的题目尤其是证明题，切入点就在于根据空间向量的选取。本文将以空间向量为依据，解决立体几何的各类型的证明题。

关键词：空间向量;立体几何;证明题;解题技巧

立体几何是高考的考试重点，我通过汇总和梳理最近几年的高考题发现，立体几何在高考题中的分值已经提高到17分左右。高中数学立体几何证明的形式有很多种，证明的程序也多半没有固定的逻辑与套路，要解决此类问题需要的理论基础和知识储备要求比较高。如此一来，对空间想象能力比较差的同学而言，便成了致命的缺点。立体几何的分数拿不到，高考得分必然受到很大的影响。通过不断的总结与思考，发现立体几何的证明题，是可以找到技巧，找到切入点的。本文，将从多个方面对立体几何的证明题的解法做出探究与详述。

立体几何的计算和证明题，往往考察的是位置关系与度量问题。其中线线垂直、线线平行、线面垂直与线面平行是立体几何中常见的考察位置关系的题目类型。而点到线的距离以及点到面的距离，是度量问题的其中一大考点，而度量线线夹角、线面夹角以及面与面所形成的角是另一主要考点。

空间向量是立体几何解题的关键，更是对于立体几何所有题目解题的突破点，也就必然成为处理立体几何问题的重要工具与方法。解题过程中，可用定量的计算代替定性的分析，由此将逻辑推理严谨的论证题得以巧妙规避。空间向量的引入在很大程度上降低了立体几何的思维难度，使解题过程具有规律可循，学生容易掌握。

基于空间向量坐标法来处理立体几何证明题的过程一般分为以下几步：第一，寻找并建立恰当的直角坐标系;第二，对于相关点的坐标求出具体数值;第三，表征向量坐标并结合公式进行计算与论证;第四，将结论向几何结论进行转化。在进行第一步时，要谨记三条直线两两垂直的交点作为切入点，在题目给出的图形中找出这三条直线。如果没有给出，就需要在图中构造出来。由此而言，基于题目所给信息，必须要充分利用题干信息，包括线线垂直关系。除此之外，建立右手空间直角坐标系，这样更符合我们的空间想象能力以及逻辑的推理。

借助空间向量能够把立体几何中的各种问题往向量的坐標运算转化，包括垂直、平行、距离、夹角等问题。具体解题思路如下所示：

通过以上例子，我们可以发现，空间向量的使用，能在很大程度上降低空间想象能力不足所带来的难题。在初步学习立体几何这一知识点时，我们首先要做的就是将每个概念与定理进行熟练掌握并分类整合，构建知识点之间的联系，问题才能迎刃而解。其次需要注意将立体几何证明题常出的考点类型与解题思路进行总结汇总，建立清晰、合理而又完整的知识系统。

立体几何证明题一般考察的是线面、面面的平行以及线线、线面、面面的垂直。在思考的过程中，首先确定针对不同的问题，应该用哪一个定理去解决，解决思维包括：正向思维、逆向思维和双向思维。简单题目，可以用正向思维来解决，比较复杂的题目可以通过逆向思维来解决。具体为把结论作为切入点，结合题干信息，寻找线索，将题干未给出的信息，通过建立直角坐标系以及空间向量的方法，标注隐含条件。逆向思维是解决立体几何证明题中最常用也是最好用的方法。对于题目所给出的题干信息之间联系性较小的题目，需要用双向思维来解决。

综上，对于立体几何证明题的解答来说，不仅需要掌握借助空间向量等方法和技巧，同时也需要多加练习，构建一种思维，多方面提升自己的能力。

参考文献

[1]杨国锋.对立体几何试题的一些分析和思考[J].数学学习与研究，2015年16期

[2]杨国栋.空间向量对立体几何教与学的影响[J].高教前言2013年04期

[3]袁国全.高中立体几何证明题的解题方法与技巧[J].中学课程辅导，2015年09期。