基于L-M算法的神经预测控制初值问题研究

许鹏　李绍铭

摘要：针对神经网络预测控制因滚动优化算法初始值选择不当而降低控制性能的问题，提出一种通过粒子群算法对初始值进行动态选取的方法。通过RBF神经网络建立预测模型，使用L-M算法滚动优化求解控制量，利用PSO算法的全局快速收敛能力动态确定L-M算法初始值，通过滚动优化的目标函数可获取粒子适应度值，实现初始值动态更新，并对权重系数λ进行实时修正。Matlab仿真实验结果表明所提方法能够解决初值选取问题，同时改善了控制系统的性能与可靠性。

关键词：模型预测;RBF;L-M算法;粒子群算法;初始值

中图分类号：TP13文献标志码：A文章编号：1008-4657（2019）02-0018-07

0引言

传统的模型预测控制（Model Predictive Control，MPC）大多基于线性预测模型，这就导致其运用范围依旧局限于线性或非线性不强的对象[1]。而实际的工业对象通常都是强非线性的，模型往往很难精确建立。神经网络从理论上来说，能以任意精度逼近复杂的非线性对象。因此，将MPC与神经网络建模相结合而形成的神经网络预测控制成为研究热点[2]。

由于神经网络模型自身便具有强非线性，这就使得在滚动优化时需要对复杂的非线性方程组进行求解来获取其最优解。因此，目前大部分的研究者都通过局部优化的方法获取次优解。如文献[3]采用拟牛顿法（Quasi-Newton，Q-N）对广义预测控制器（Generalized Predictive Control，GPC）进行优化。文献[4]采用L-M和Q-N算法进行滚动优化改进，对系统的抗干扰能力有所提高。文献[3-4]采用上一时刻的控制量作为优化算法的初值来获取控制量，得到不错的控制效果，但皆未明确指出确定初值的方法。

在对神经网络预测控制进行研究时发现，在滚动优化部分，算法初值选取对整个控制系统的性能有较大影响。在使用文献[3-4]中所采用的以上一时刻的控制量作为初值的方法来进行实验时出现控制性能下降的情况。

为解决该问题，本文提出利用粒子群算法动态获取优化算法的初始值。

1神经网络预测控制

1.1预测模型

4.1建模

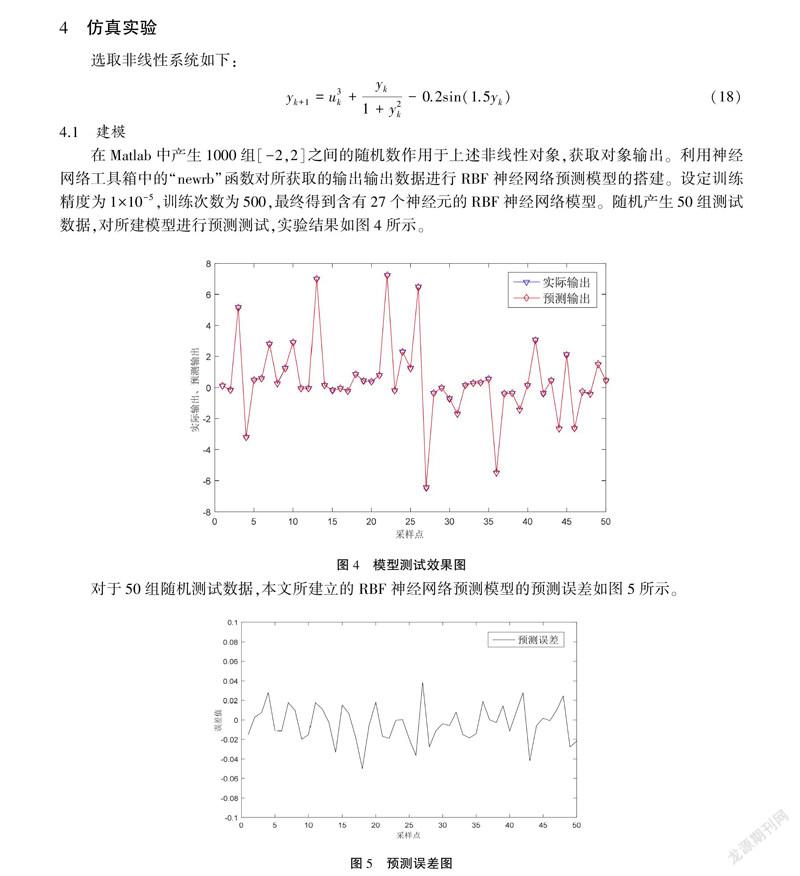
在Matlab中产生1000组[-2，2]之间的随机数作用于上述非线性对象，获取对象输出。利用神经网络工具箱中的“newrb”函数对所获取的输出输出数据进行RBF神经网络预测模型的搭建。设定训练精度为1×10-5，训练次数为500，最终得到含有27个神经元的RBF神经网络模型。随机产生50组测试数据，对所建模型进行预测测试，实验结果如图4所示。

对于50组随机测试数据，本文所建立的RBF神经网络预测模型的预测误差如图5所示。

其模型准确率为99.04%，累计误差为0.3029，表明本文所建立的模型精度较高，能够满足预测控制要求。

4.2仿真结果

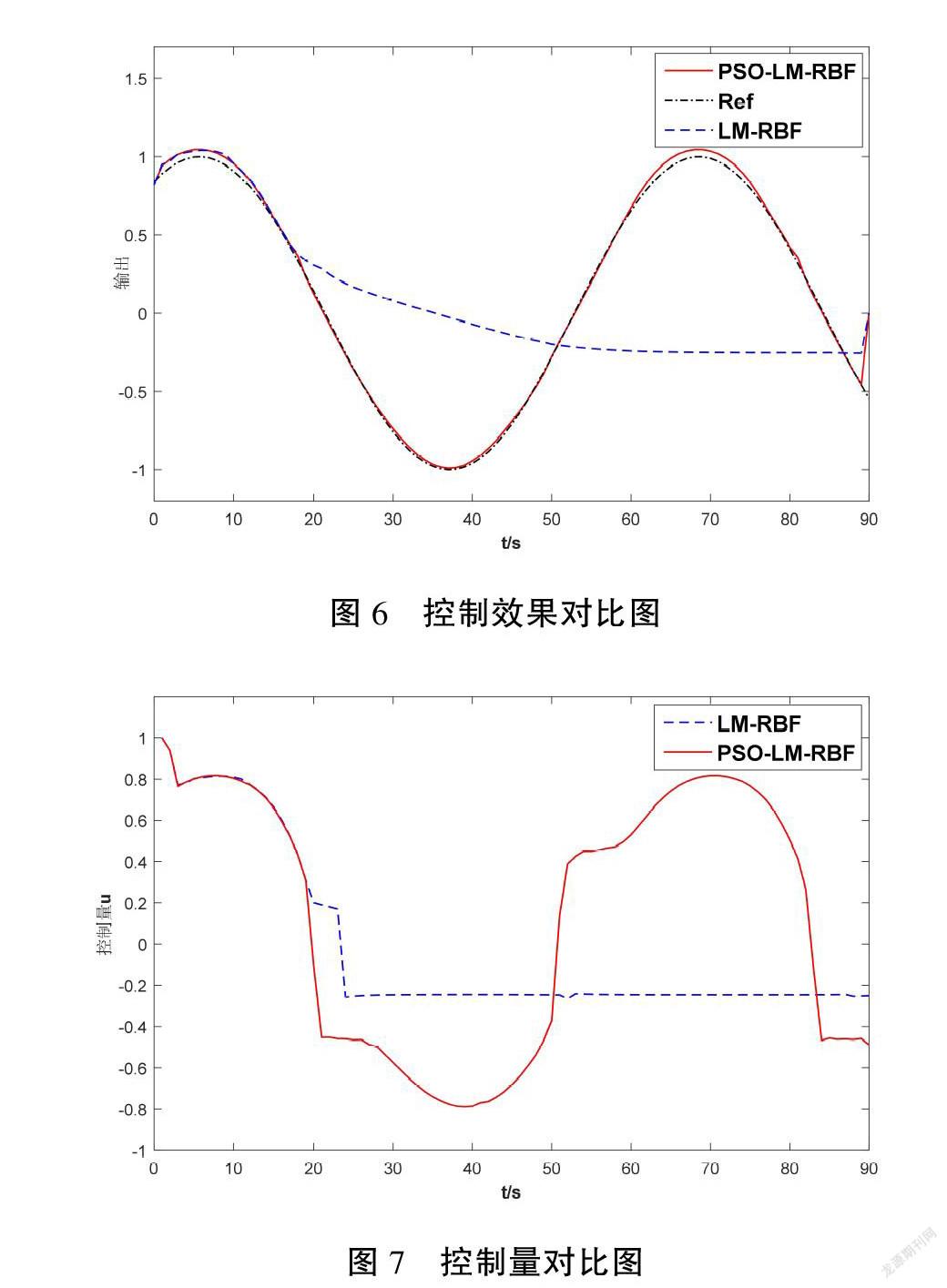
为比较文献[3-4]的初值确定方法与本文所提方法的区别，将二者对比实验，让其跟踪相同正弦波信号。

由图6可知，文獻[3-4]中所使用的以上一时刻的控制量作为初始值的方法，出现了无法跟踪期望输出的问题，控制性能下降，由图7可知，出现该情况是由于控制量不变所导致，即上文中初始值选在了C点造成;对比可知，本文所采用的使用PSO算法动态获取L-M优化算法初始值的方案不仅能够实现有效地跟踪，并且响应很快，误差较小，解决了初值问题，并显现出较为理想的控制效果。

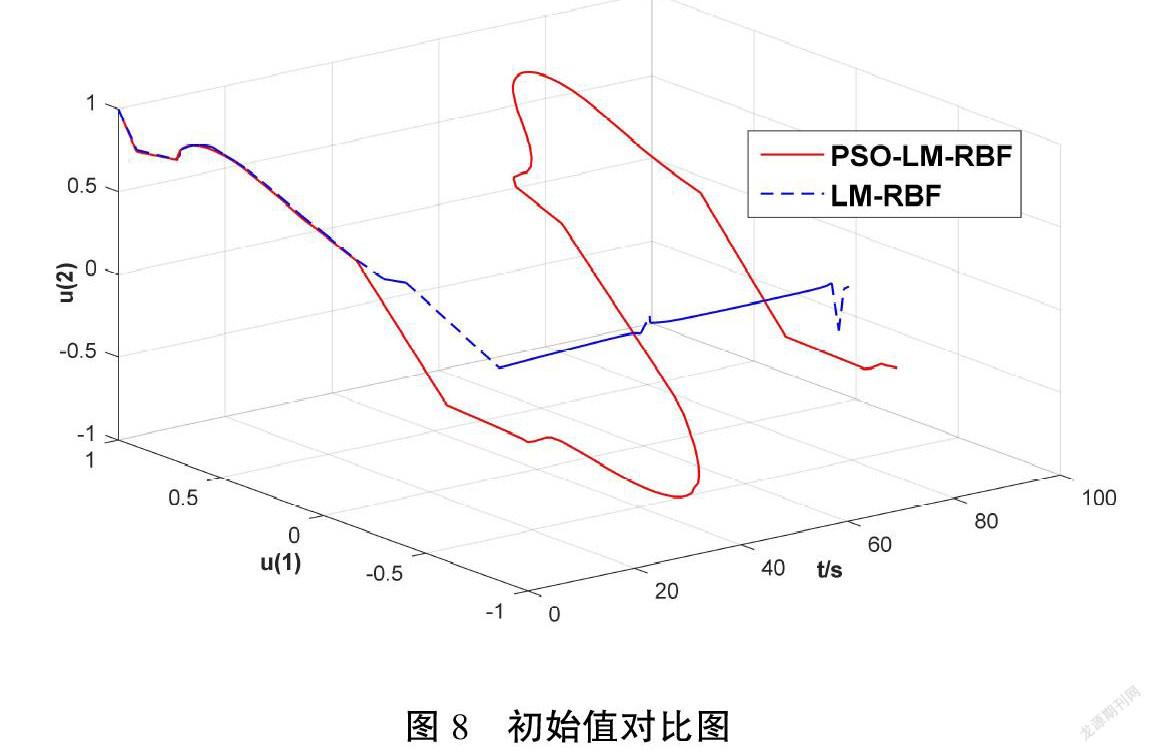
为更清楚的看出初值选取不同，绘制两种方法在实验过程中的初始值选取点，如图8所示。

通过将图8与图7进行比较可以看出，文献[3-4]所使用的方法，初始值在约20s之后便不再改变，从而导致初值问题的发生;而本文所采用方法能够获取较为理想的初值。在仿真实验中，若加大迭代代数，通过PSO算法所获取的初值将愈发接近L-M算法优化得到的控制量，但迭代次数的增加会影响实时控制，本文通过仿真试验发现选取迭代数为10便可获得较为满意的控制效果。

通过上述实验结果分析可知，本文所提出的使用PSO算法获取初始值的方案能够有效的解决神经网络预测控制滚动优化部分初始值的选取问题，并且对控制器的性能及稳定性有一定程度的提高。

5结论

将L-M算法和PSO算法相组合，利用PSO算法的全局快速收敛能力，将其寻优得到的最优粒子作为L-M算法的初始值，实现初始值动态更新，再利用了L-M算法在接近局部极小值时收敛速度快、搜索精度高等优点实现控制量的最优选取，并对权重系数λ进行实时修正，解决了L-M算法依赖初值问题。通过Matlab进行仿真实验，将文献[3-4]中所使用的方法与本文所提出的方案做对比，结果表明了本文所提出的方法能够有效地解决神经网络预测控制中优化算法的初始值选取问题，改善了系统的控制性能，并且提高了神经网络控制系统的可靠性。

参考文献：

[1] 席裕庚.预测控制[M].第2版.北京：国防工业出版社，2013.

[2] 戴文战，娄海川，杨爱萍.非线性系统神经网络预测控制研究进展[J].控制理论与应用，2009，26（5）：521-530.

[3] Srensen P.H，Nrgaard M，Ravn O，et al.Implementation of Neural Network Based Non-linear Predictive Control[J].Neurocomputing，1999，28（1）：37-51.

[4] Nand K，Singh S P.Simulated Response of NN Based Identification and Predictive Control of Hydro Plant[J].Expert Systems with Applications，2007，32（1）：233-244.

[5] 王炳萱，李国勇，王艳晖.基于LM-PSO算法和BP神经网络的非线性预测控制[J].太原理工大学学报，2016，47（2）：207-211.

[6] 刘金琨.RBF神经网络自适应控制MATLAB仿真[M].北京：清华大学出版社，2014.

[7] 宫赤坤，闫雪.基于RBF神经网络的预测控制[J].上海理工大学学报，2005，27（5）：421-424.

[8] 张日东，王树青.基于神经网络的非线性系统多步预测控制[J].控制与决策，2005，20（3）：332-336.

[9] Zhang Pengyuan，Xi Yugeng，Li Dewei.Closed-loop Robust Model Predictive Control for Time-delay Systems with Structured Uncertaines[J].Control Theory & Applications，2013，30（6）：683-692.

[10] 张昭昭，乔俊飞，余文.基于LM算法的在线自适应RBF网结构优化算法[J].控制与决策，2017，32（7）：1 247-1 252.

[11] 高异，杨延西，刘军.模糊遗传滚动优化的LS-SVM预测控制研究[J].系统仿真学报，2007，19（6）：1 277-1 280.

[12] 樊兆峰，马小平，邵晓根.神经网络预测控制局部优化初值确定方法[J].控制理论与应用，2014，31（6）：741-747.

[责任编辑：许立群]