基于主成分分析模型的高职数学课信息化教学评价

摘  要：信息化在高职数学课中不断的发展迫切需要建立符合高职数学课特点的评价体系，针对于此，本文提出了注重基础、突出应用、强化跟踪为核心的信息化教学评价体系，该评价体系分为9个评价指标，据此指标，以某高职院校的5名数学教师为例，建立了主成分分析模型，此模型均具有客观性强，易操作的特点，这对高职数学信息化教学定性和定量评价有较强的借鉴作用，也对进一步提高高职数学信息化教学水平有着十分重要的意义。

关键词：数学信息化教学;教学评价;主成分分析法

中图分类号：G434;TP399      文献标识码：A 文章编号：2096-4706（2019）23-0101-03

Higher Vocational Mathematics Course Information Teaching Evaluation

Based on the Principal Component Analysis Model

FENG Qiang

（Weifang Vocational College，Weifang  262737，China）

Abstract：The continuous development of informatization in higher vocational mathematics course urgently needs to establish an evaluation system which is in line with the characteristics of higher vocational mathematics course. In view of this，this paper puts forward an evaluation system of informationization teaching，which focuses on the basis，highlights the application and strengthens the tracking. The evaluation system is divided into nine evaluation indicators. Based on these indicators，five mathematics teachers in a higher vocational college are taken as an example to establish the principal component model. This model is objective and easy to operate. It can be used for reference in qualitative and quantitative evaluation of mathematics informatization teaching in higher vocational colleges. It is also of great significance to further improve the level of mathematics informatization teaching in higher vocational colleges.

Keywords：mathematics informationized teaching;teaching evaluation;principal component analysis

0  引  言

隨着信息化与网络技术的发展，高职院校高等数学课也逐渐从传统教学模式向信息化教学模式过度，尤其是近几年，随着智能手机的普及化以及大量网络课程资源及对应APP的出现，很多高职院校高数教师针对此现状从教学组织、教学内容、教学方法、教学反馈等各方面做了对应的改革，与之对应的高职数学课的信息化教学评价也要适应此形式，从而更好的引导以促进高职数学课的教学。

1  高职数学课教学评价指标构建

区别于传统的教学评价，信息化教学化评价更注重多维度综合评价高职数学课，通过对信息化教学背景下高职数学课的分析，并根据人才培养方案和课程标准，建立了以注重基础、突出应用、强化跟踪为核心的信息化教学评价体系，此评价体系在评价指标中更加侧重了多媒体资源及网络资源的有效使用，依此，设定9个评价指标，如表1所示。

针对此9个目标采用主成分分析法进行评价。

2  资料的来源

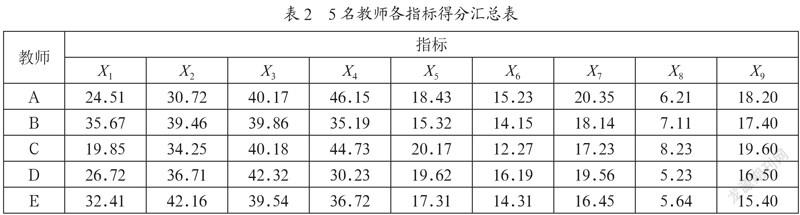
该文章资料来自于对5名某职业院校高数教师任课班级情况调查，这5名教师分别用字母A、B、C、D、E表示，X1至X9各指标的分值来源于校内外专家及同行评价。X1至X9均为高优指标，故不必进行同趋势化处理。

3  基于主成分分析模型的信息化教学评价

主成分分析法是将原来变量重新组合成一组新的相互无关的几个综合变量，同时根据实际需要从中可以取出几个较少的总和变量并尽可能多地反映原来变量的信息的统计方法。这是数学上处理降维的一种方法，主成分分析法可以消除变量间的相关影响，所以在指标选择上相对容易些。

首先将校内外专家及同行教师对A、B、C、D、E这5名教师的X1至X9各指标评价得分汇总，如表2所示。

利用SPSS软件处理数据，得X1—X9相关系数矩阵如表3所示。

从表3中可以看出教学资料X1与教学过程X2;后续发展度X6与教学方法X3及实际结合度X7;在线答疑指导学习X9与课后作业完成情况X8及信息网络资源X4存在着显著关系，这说明这几个指标信息存在着重叠，这是符合实际的，表4为公因子方差矩阵。

从表4可以看出各个指标的提取率是非常高的，这说明信息得以充分的提取。

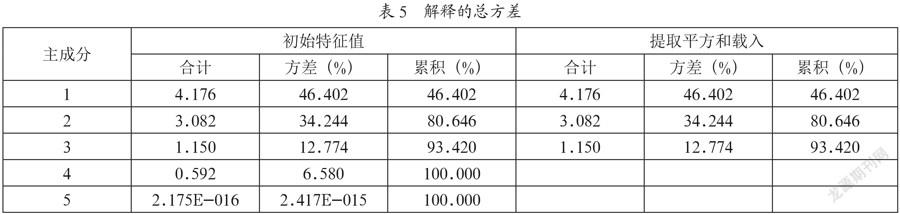
对表1至表4中数据进行分析得到表5，并提取前三个主成分。

表5中可以看出前三个主成分的累计贡献率达到了93.420%，这说明降维后信息保持率维持较高水平。表6为初始因子载荷矩阵。

由表6可以看出信息网络资源X4、专业结合度X5、课后作业完成情况X8、在线答疑指导学习X9这四个指标在主成分上F1有较高载荷，说明主成分F1基本反映了这些指标的信息;教学方法X3、后续发展度X6、课后作业完成情况X8在主成分F2上的载荷较高，说明主成分F2基本反映了这三个指标的信息;信息网络资源X4、实际结合度X7在主成分F3上的载荷较高，说明主成分F3基本反映了这两个指标的信息。

用成分矩阵中的数据除以主成分相对应的特征值开平方根便得到三个主成分中每个指标所对应的系数，即为对应的特征向量，将得到的特征向量与标准化后的数据对应相乘得到主成分表达式：

F1=-0.41X1-0.37X2-0.07X3+0.41X4+0.28X5-0.30X6+0.05X7+0.37X8+0.46X9

F2=-0.23X1-0.31X2-0.49X3-0.10X4+0.32X5+ 0.43X6+0.47X7-0.31X8-0.01X9

F3=0.29X1-0.32X2-0.35X3+0.32X4-0.53X5+0.24X6+ 0.49X7-0.20X8+0.09X9

從而得到权重综合模型：

（λ1=4.176，λ2=3.082，λ3=1.150）

即：F=0.497F1+0.367F2+0.138F3

根据得出的主成分综合模型可计算综合主成分值，并对这5名教师进行排序，进行综合评价比较，结果如表7所示。

对得出的综合主成分（评价）值，可用已有的经验与原始数据做聚类分析进行检验，对有争议的结果，可采用其他的评价方案解决争议。

4  结  论

在主成分分析中，所提取的前3个主成分的累计贡献率达到了93.420%，首先这说明变量降维后的信息量保持在一个较高水平上，其次这些被提取的主成分能否符合当前高职数学信息化教学的规律及实际，与专家评议打分有着一定的关系;另外主成分解释其含义一般多少会带点模糊性，不像原始变量的含义那么清楚、确切，这是变量降维过程中不得不付出的代价;再次主成分分析法评价效果的好坏也与指标之间相关程度有关，一般情况下指标之间相关程度越高，主成分分析效果越好，而主成分分析法具有可消除各个变量之间相关影响、减少指标选择工作量、评价权重客观、计算比较规范、便于在计算机上实现的优点。

参考文献：

[1] 王青华，向蓉美，杨作廪.几种常规综合评价方法的比较 [J].统计与信息论坛，2003（2）：30-33.

[2] 杨德芹.教学质量评价模型及案例分析应用研究 [D].武汉：华中师范大学，2008.

[3] 周源.职业院校信息化课堂教学有效性研究 [J].信息与电脑（理论版），2015（21）：170-171+173.

[4] 邱东.多指标综合评价方法 [J].统计研究，1990（6）：43-51.

作者简介：冯强（1979-），男，汉族，山东青州人，讲师，硕士，研究方向：应用数学教学与研究。