基于ANSYS Workbench的不同形式压力容器封头的应力分析

邵海磊　郭海伟

摘 要：本文运用ANSYS Workbench有限元分析软件对储氢罐压力容器在单位压力（1MPa）下的应力状态进行分析，得到了椭圆封头和球形封头形式下的筒体和封头内壁上的应力分布状况。同时，对不同半轴长度的椭圆封头压力容器的径向、切向和周向应力进行计算，并与球形封头的应力分布进行对比分析，得到了应力分布较好的封头形式。

关键词：压力容器;封头;应力分析;ANSYS Workbench

中图分类号：TQ051.303 文献标识码：A 文章编号：1003-5168（2019）23-0055-04

Stress Analysis of Different Pressure Vessel Head

Based on ANSYS/Workbench

SHAO Hailei GUO Haiwei

（Zhengzhou Siwei New Material Technology Research Institute Co.，Ltd.， Zhengzhou Henan 450000）

Abstract： This paperused ANSYS Workbench finite element analysis software to analyze the stress state of hydrogen storage tank pressure vessel under unit pressure （1MPa）， and obtainedthe stress distribution on the inner wall of the cylinder and the head under elliptical head and spherical head. At the same time， the radial， tangential and circumferential stresses of the elliptical head pressure vessels with different half-axis lengths were calculated， and compared with the stress distribution of the spherical head， the form of the head with good stress distribution was obtained.

Keywords： pressure vessel;dish head;stress analysis;ANSYS Workbench

纖维增强树脂基复合材料具有强度高、重量轻的优点，人们可以采用复合材料作为储氢罐的罐体材料[1]。由于复合材料具有明显的各向异性特征[2]，因此人们需要对罐体的应力分布状态进行计算分析，然后根据应力分布状态对复合材料的铺层厚度和角度进行设计[3-6]。

金属材料压力容器的封头通常采用平形或者椭圆形，但是只能承受较小的压力[7，8]。对于高压容器而言，球形封头更为合适，由于纤维材料可以用于复杂结构的设计及制造，因此人们可以采用纤维缠绕成型的方法制作不同封头形式的复合材料压力容器。

本文针对不同封头形式的压力容器进行应力分析，得到封头与筒身部分的径向、切向和周向应力，然后对以上三个方向的应力分布情况进行对比分析，最终选择一种应力分布较为均匀的封头形式，为复合材料压力容器的设计提供理论基础。

1 建立有限元模型

根据国际压力容器技术理事会提供的目前已经量产的复合材料储氢罐资料，建立有限元模型，其尺寸参数如表1所示。

该储氢罐是由T800级碳纤维增强树脂基复合材料通过缠绕的方式制作而成。本文主要对封头部分进行研究，为了减少有限元分析的计算时间，本分析采用的材料为金属材质，取容器封头部分建立有限元分析模型，结构示意图如图1所示。图中，数值单位均为mm。

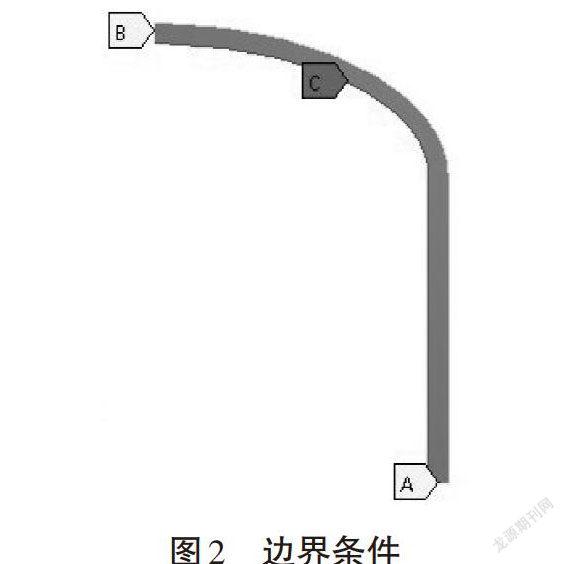
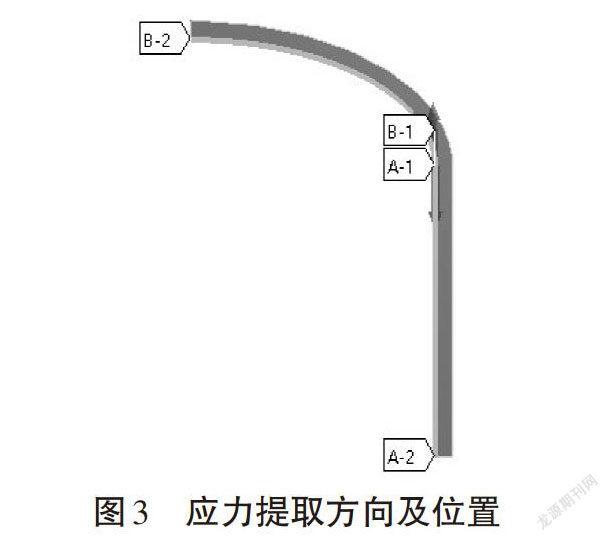
罐体模型为轴对称结构，边界条件的施加如图2所示，内表面A施加1MPa的单位压力，在对称线B上施加轴向的对称约束，在轴对称线B上施加水平方向的对称约束。提取的应力值位置如图3所示，其中A-1和B-1的位置为筒身和封头的连接点处，A-1到A-2方向为筒身上的应力分布点，B-1到B-2为封头上的应力分布点，筒身部分位置坐标设为负值，封头部分位置坐标设为正值。

2 椭圆封头压力容器的应力分析

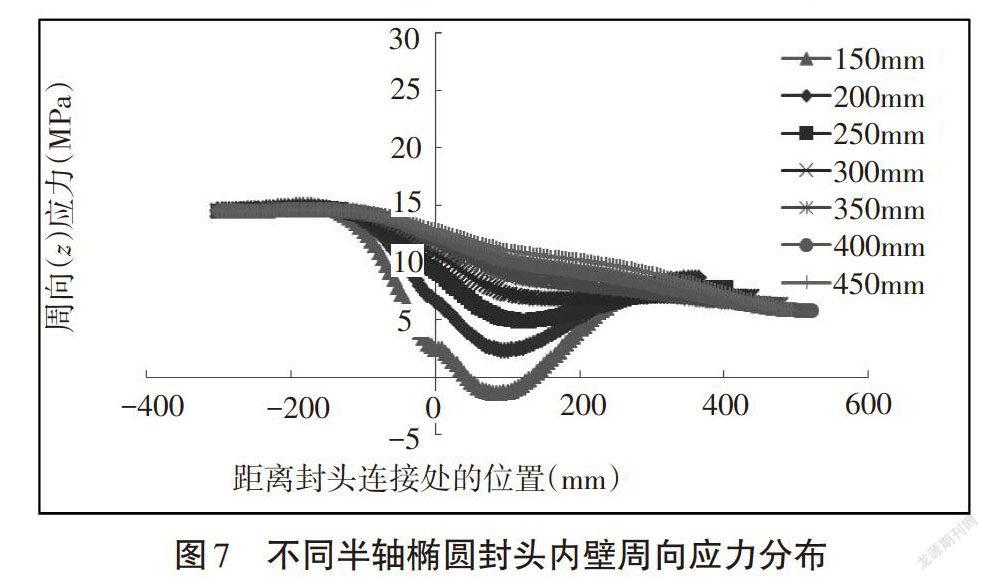
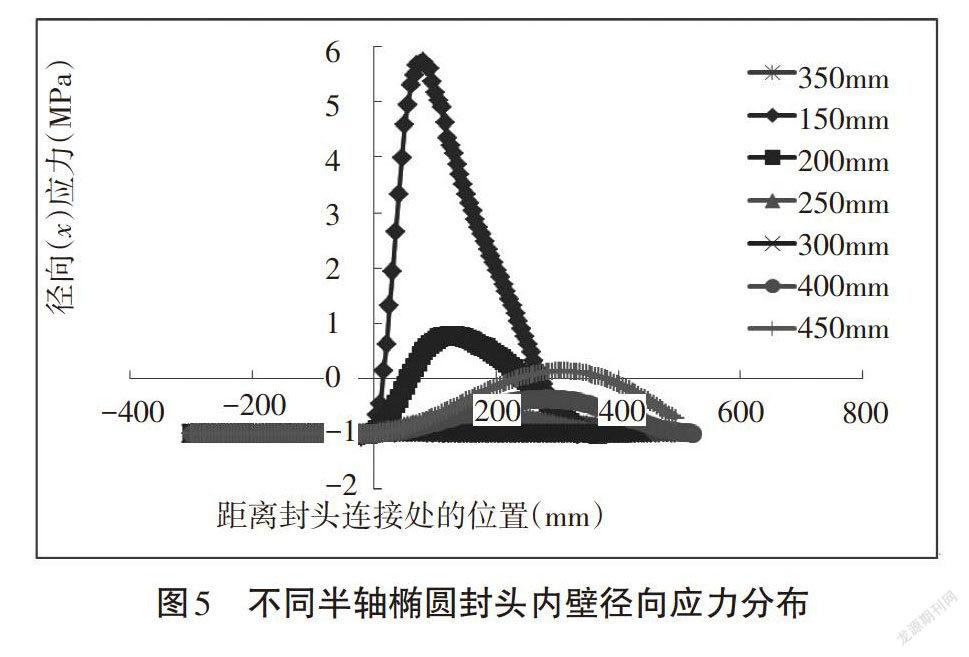
本文对椭圆形封头的压力容器模型进行静态结构分析，得到了横截面上的等效应力云图，如图4所示。由此可以看出，椭圆形封头容器在筒体及封头中心部分存在较高的应力;在封头与筒身的接触部分，内壁存在一个较小的应力集中区域，外壁上的应力值最小。在不同短半轴情况下，椭圆形封头内壁上的径向、切向和周向应力分布分别如图5、图6和图7所示。

由图5可以看出，径向应力在筒身部分几乎保持不变，封头部分出现应力集中现象。随着椭圆半轴的增加，封头呈球形时，筒体部分的径向应力保持不变，椭圆封头上接近筒身的连接点处的径向应力逐渐减小，并且在封头为球形时，封头与筒身的径向应力相等。随着椭圆半轴的长度大于筒身半径，封头部分的径向应力又开始逐渐变大。

由图6可以看出，内壁上切向应力的分布呈“W”形，切向应力在筒身部分基本保持不变，在与封头的接触处逐渐减小，过了连接点后快速增加，然后急剧下降，再趋于稳定，在连接点处存在应力集中现象。随着椭圆半轴的增大，应力集中现象逐渐减小，在身与封头上的切向应力分布也越均匀。

由图7可以看出，周向应力在筒身部分最大，当椭圆封头的短半轴较小时，在靠近筒体与封头的连接点处，周向应力迅速减小，最小周向应力位于封头上，然后逐渐增大，封头部分的最大周向应力位于封头中心处;在封头的短半轴大于筒身半径时，随着短半轴的增加，周向应力由筒身至封头的分布更加平滑。

为了便于复合材料压力容器纤维铺设的设计，人们需要对储氢罐封头部分内壁与外壁上的最大周向应力值进行分析，探究最大周向应力与椭圆封头半轴长度之间的关系规律，如图8所示。随着半轴长度的增加，容器封头内壁最大周向应力呈现先增加后减小再逐渐增大的趋势，整体上最大应力值变化范围较小。从封头外壁的最大周向应力曲线可以看出，当椭圆封头的半轴较小时，封头的最大应力值较大，当封头接近球形时，应力值最低，继续增加椭圆封头的长度并不能再降低最大应力值，却会产生最大应力值逐渐增加的效果。

3 球形封头压力容器的应力分析

本研究对球形封头压力容器进行了静态结构分析，得到了球形封头压力容器内壁上的等效应力云图，如图9所示。球形封头罐体在筒体部分应力较大，在封头部分应力较小，在封头与筒体连接处未出现明显的应力集中现象。

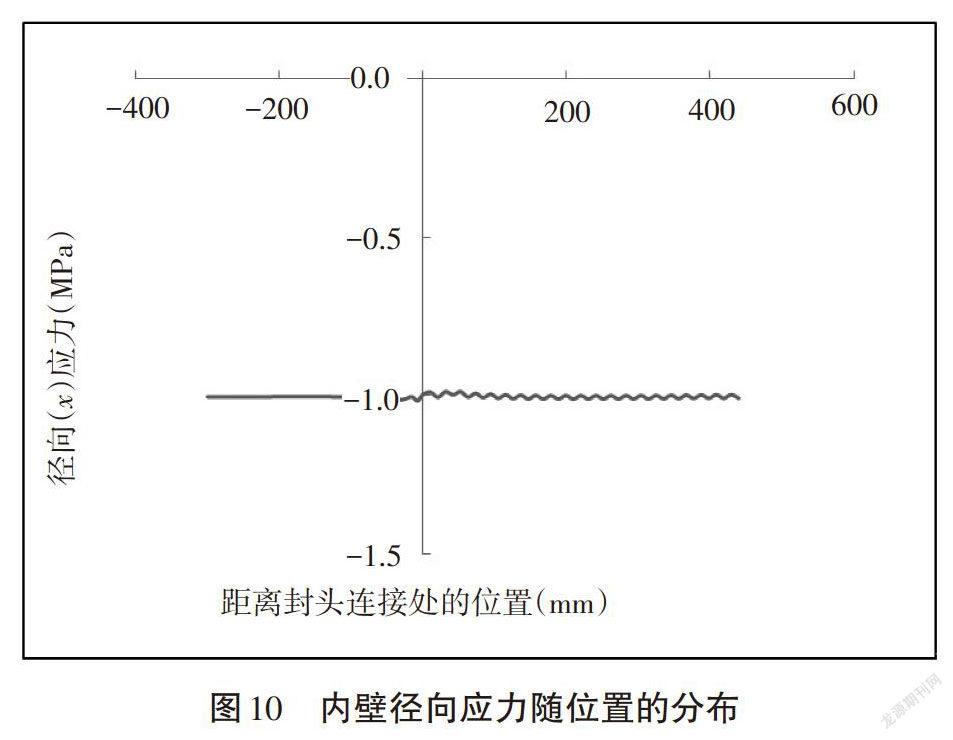
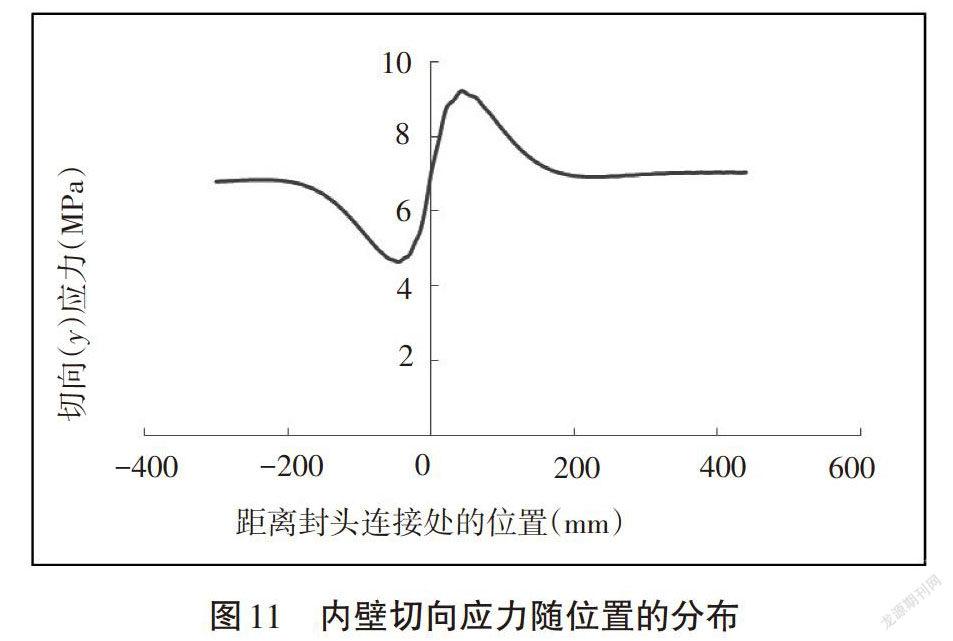
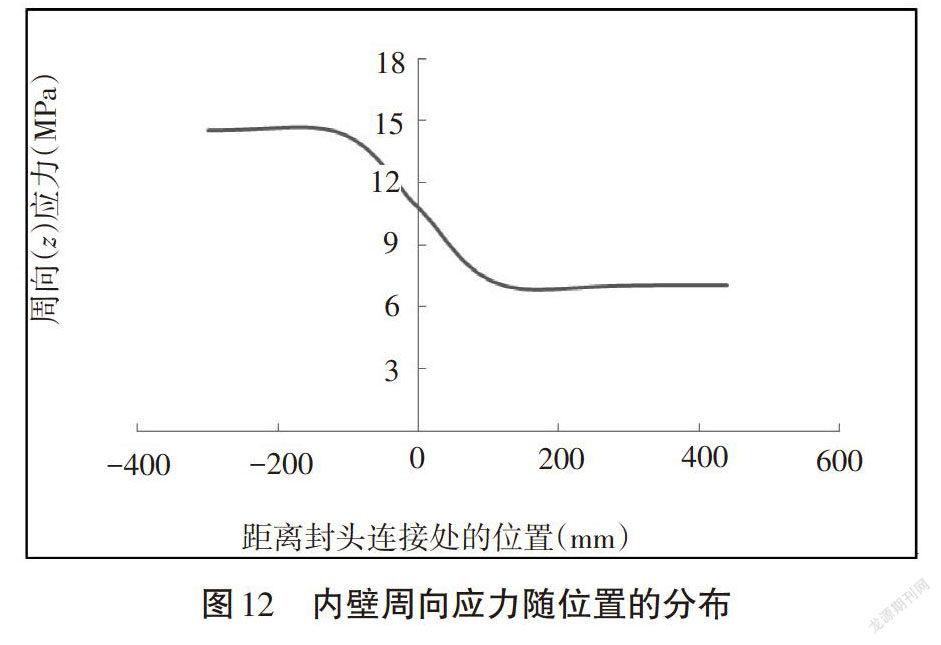
对球形封头压力容器内壁上的径向、切向和周向应力进行计算分析，所得结果如图10、图11和图12所示。

由图10可以看出，球形封头在径向上的应力几乎保持不变，与施加到内壁上的压力相等，但是筒体与封头的连接处出现了应力不连续的现象，封头上出现了应力在极小范围内跳动的现象，但是不影响整体的应力分布。

由图11可以看出，随着位置的变化，在筒身与封头的连接处，内壁上切向应力先减小后快速增加，然后急剧下降，再趋于稳定，封头与筒身的连接点处存在应力集中现象。球形封头的最大切应力约为内压的9倍，位于靠近连接点的封头上，整体切应力为内压的7倍左右，最小切应力为内压的4.5倍左右，在靠近连接点的筒身上。

由图12可以看出，周向应力在筒体部分为内压的15倍左右，在靠近连接点处，周向应力迅速减小并趋于稳定，最小周向应力位于封头上，为内压的7倍左右。

4 結论

根据压力容器常用的椭圆封头与球形封头，本文进行了容器内壁的径向应力、切向应力和周向应力的应力分布有限元模拟，得到了以下结论：当椭圆形封头椭圆度较大时，封头与筒体的连接处会出现明显的应力集中现象，椭圆度越小，越接近球形，径向应力和周向应力表现得越均匀;球形封头的各向应力分布都比较均匀，应力集中现象与其他形式的封头相比有明显的减小，比较适用于高压容器，所得结果可以给复合材料压力容器纤维铺放设计提供理论参考。

参考文献：

[1]于斌，刘志栋，靳庆臣，等.国内外空间复合材料压力容器研究进展及发展趋势分析（一）[J].压力容器，2012（3）：30-41.

[2]沈观林，胡更开，刘彬.复合材料力学[M].北京：清华大学出版社，2013.

[3]陈亮.碳纤维复合材料缠绕气瓶数值分析[D].大连：大连理工大学，2013.

[4]祖磊，穆建桥，王继辉，等.基于非测地线纤维缠绕压力容器线性设计与优化[J].复合材料学报，2016（5）：1125-1131.

[5]林张欢.复合材料压力容器有限元分析及其优化设计[D].武汉：华中科技大学，2014.

[6]马国峰，姜广祥，费春东，等.纤维缠绕环形压力容器复合材料结构设计[J].玻璃钢/复合材料，2012（2）：40-43.

[7]高勇，黄盛鹏，汤吉祥，等.封头型式对压力容器应力影响的有限元分析[J].内蒙古石油化工，2018（6）：38-40.

[8]罗彩霞，梅瑛，许志珍.高压容器筒体与封头连接处有限元分析及优化[J].压力容器，2011（8）：35-38.