基于粒子群算法优化Kriging模型的桥梁钢筋锈蚀可靠度分析

王剑波，缪建家，阚毓锋，陆 洋

(苏交科集团股份有限公司 南京市 211112)

0 引言

桥梁在服役过程中承受着车辆荷载和环境不利因素的作用，其承载能力和力学性能不断退化，关于桥梁结构性能劣化机理和损伤研究日趋完善。其中，钢筋锈蚀作为桥梁性能的重要研究内容之一，其可靠性研究对桥梁适用性评价具有重要的意义。能够准确反映桥梁状态，为养护管理提供依据。

焦俊婷等[1]考虑了环境温度、相对湿度对钢筋锈蚀的影响，对简支桥梁钢筋锈蚀寿命可靠性进行了研究，并分析了随机变量的灵敏度，确定了各因素对钢筋锈蚀寿命的影响程度。张克波等[2]对一座氯离子盐侵蚀作用下的钢筋混凝土简支T梁桥抗力可靠度进行了研究，考虑了主筋、箍筋对结构抗力的贡献程度，分析了其抗力和可靠度随时间的变化规律。云永琥等[3]利用改进Kriging模型和有限元方法对热结构耦合梁共振非概率可靠性进行了分析，通过Kriging模型解决了状态函数为隐式形式的难题。贾布裕等[4]提出了Kriging模型改进响应曲面方法，结合首次超越结构破坏准则构建了桥梁地震动力响应功能函数，计算并分析了桥梁地震动力可靠度。王磊等[5]针对检测数据不完备而无法准确获得变量统计参数的问题，提出了基于模糊理论的桥梁时变可靠性分析方法，并通过Monte-Carlo方法进行计算。陆春华等[6]在现有氯离子扩散研究基础上，利用Monte-Carlo抽样模拟方法对锈蚀钢筋混凝土结构全寿命成本进行了分析。

针对桥梁钢筋锈蚀适用性可靠度分析问题，本文主要考虑了钢筋直径、混凝土抗压强度、保护层厚度和沿筋方向裂缝宽度等影响因素，通过粒子群优化Kriging方法结合实际检测数据，建立了钢筋锈蚀程度的极限状态方程。采用Monte-Carlo方法求解桥梁钢筋锈蚀可靠度，分析了所提出方法的适用性和准确性，研究了各因素对桥梁适用性可靠度的影响程度。

1 基于粒子群算法优化Kriging模型

1.1 Kriging模型

Kriging模型[4]于1951年由南非地质学者Krige首次提出，并广泛应用于地质统计学领域。早期在工程结构中主要用于解决确定性问题，直至本世纪初才被应用到结构可靠度计算中。

一般情况下，Kriging模型主要由回归模型和随机误差两部分组成：

(1)

式中：x=[x1,x2,K,xk]T；P和k分别表示样本数量和变量参数的数量；β代表回归参数的向量形式；fT(x)为回归模型的多项式函数向量；z(x)为随机误差且服从正态分布N(0,σ2)，其协方差非零，如式(2)所示：

cov(z(xi),z(xj))=σ2R(xi,xj) i,j=1,2,K,k

(2)

式中：R(xi,xj)为任意两个参数向量xi和xj间的相关函数。相关函数包括线性模型、样条曲线模型和高斯模型等，常用模型为高斯模型，其形式为：

(3)

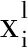
通过变量样本x及其响应值y(x)对任意变量参数取值下响应值进行无偏估计，即：

(4)

式中：c=c(x)∈Rm。为了确保响应预测值的无偏性，应满足预测值与真实值差值为零的条件。且偏差的均方差可表示为：

(5)

式中：r(x)=[R(θ,d1,x),…,R(θ,dk,x)]T，d表示待测点样本取值；R=R(θ,xi,xj)。

于是，可得任意变量对应的响应预测值为：

(6)

1.2 粒子群算法

粒子群算法[7]由Kennedy和Eberhart提出，属于进化算法的一种，具有算法结构简单、寻找最优解速度快的优点。假设粒子群是由N个粒子组成的，第i个粒子可由D维向量表示：

pi=(pi1,pi2,K,piD) i=1,2,K,N

(7)

在每次迭代中不断更新粒子的速度和位置来寻求最优解，第t+1代中第i个粒子的速度向量vi和位置向量pi分别如式(8)和式(9)所示：

vi(t+1)=wvi(t)+c1r1(pibest-pi(t))+c2r2(pgbest-pi(t))

(8)

pi(t+1)=pi(t)+vi(t+1)

(9)

式中：w为惯性权重系数；c1和c2为加速常数(一般有c1=c2=2)；r1和r2是两个相互独立的随机变量，均服从取值在[0,1]之间的均匀分布；pibest代表第i个粒子的个体最优解；pgbest代表全局最优解。

惯性权重系数w随着迭代次数的增加从最大值wmax线性递减至最小值wmin：

(10)

式中：wmax=0.9，wmin=0.4；t和Tmax分别表示当前迭代次数和最大迭代数。

1.3 粒子群算法优化Kriging模型

利用Kriging方法对实际钢筋锈蚀检测数据进行模拟，以构建钢筋锈蚀程度与影响因素间的量化关系。Kriging模型中的相关性参数θ决定着预测响应值精度，采用粒子群算法搜寻最优相关性参数，通过最优解建立模型可以提高模拟精度和可靠度计算结果的准确性。

这里以钢筋锈蚀影响因素：钢筋直径、混凝土抗压强度、保护层厚度和沿筋方向裂缝宽度作为Kriging模型的输入变量，钢筋锈蚀程度作为响应值，以及粒子群算法寻找到的最优相关性参数建立钢筋锈蚀程度预测模型。采用Kriging方法预测值与真实响应值的误差作为评价Kriging模型拟合精度的适应度函数。具体流程如图1所示。

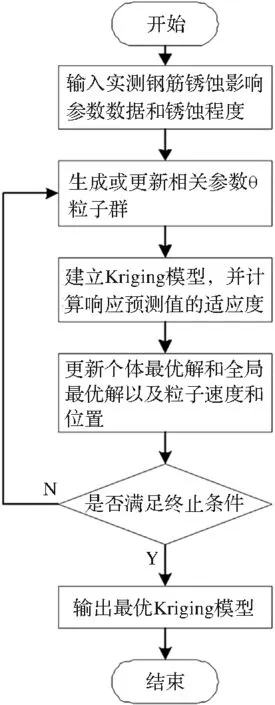
图1 钢筋锈蚀最优Kriging模型流程图

2 桥梁钢筋锈蚀Kriging模型建立

2.1 钢筋锈蚀实测数据

采用文献[7]中的某简支桥梁实测钢筋锈蚀程度及其影响因素数据进行分析，部分实测数据如表1所示。其中，D、fc、c、ω和η分别代表钢筋直径、混凝土抗压强度、保护层厚度、沿筋方向裂缝宽度和钢筋锈蚀率。

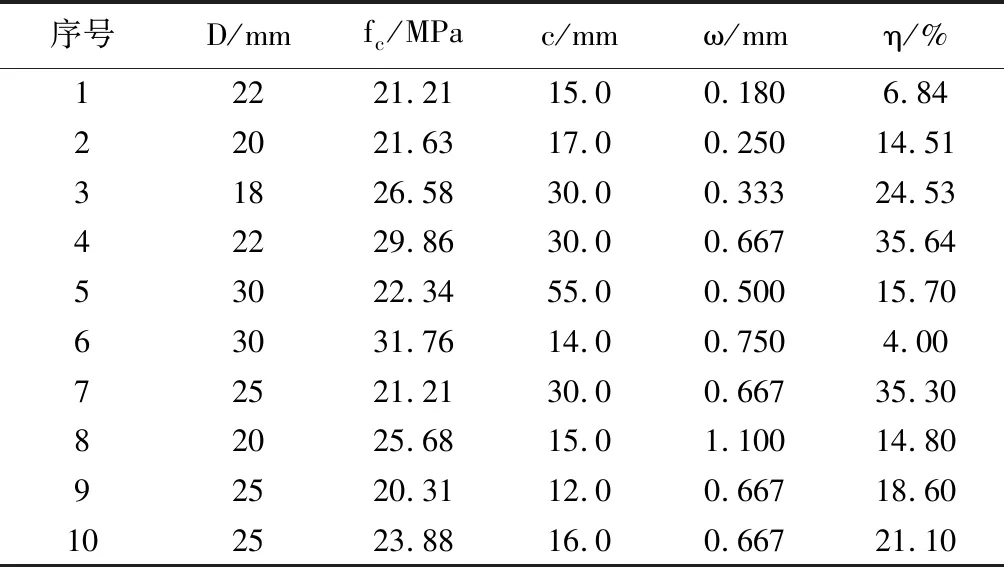
表1 钢筋锈蚀影响因素实测数据

2.2 钢筋锈蚀参数分布检验

采用频数直方图和K-S假设检验方法对钢筋锈蚀影响因素分布类型进行识别，分别判断是否服从正态分布、对数正态分布和伽马分布等常用分布类型，参数数据直方图及分布曲线如图2所示。

从图2可以看出，钢筋直径数据近似对数正态分布和伽马分布，混凝土抗压强度直方图与三种分布类型都接近，保护层厚度更符合对数正态分布，沿筋方向裂缝宽度更接近正态分布。K-S假设检验结果显示钢筋直径和保护层厚度服从对数正态分布；混凝土抗压强度和沿筋方向裂缝宽度服从正态分布且不拒绝服从伽马分布。具体钢筋锈蚀影响因素分布类型及参数如表2所示。

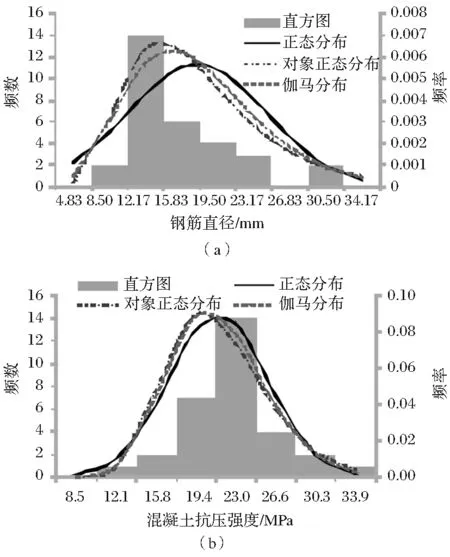
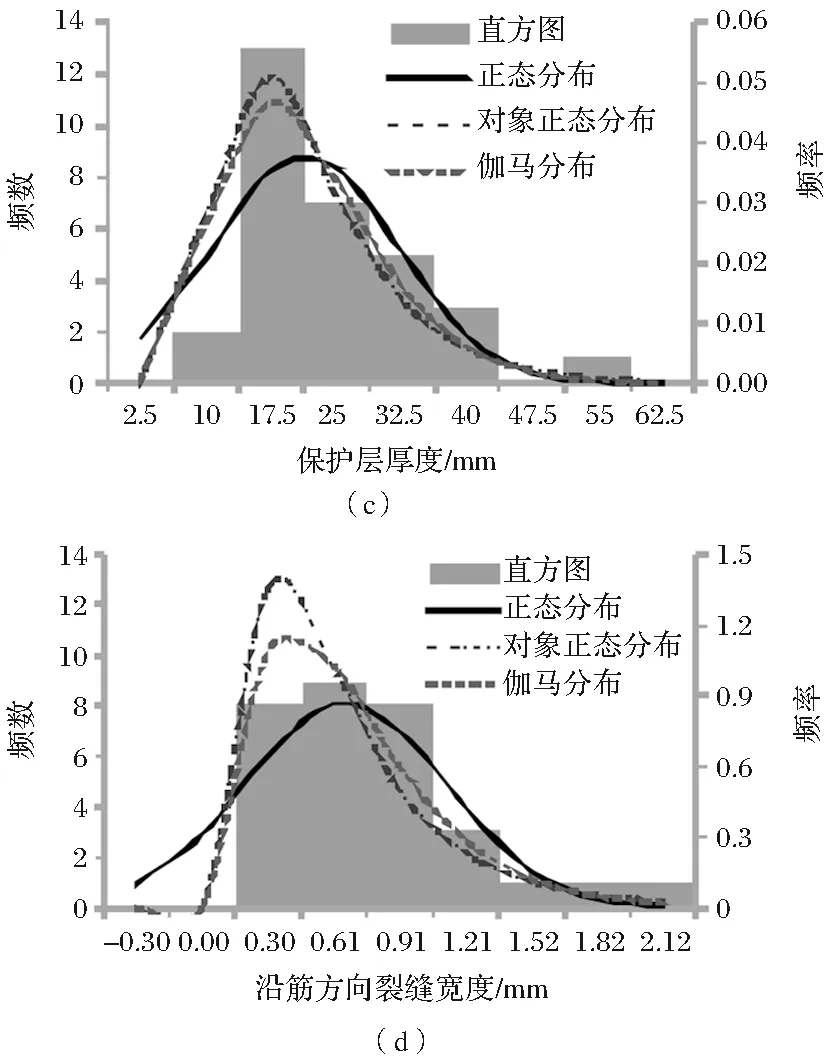
图2 钢筋锈蚀影响因素直方图及分布曲线

表2 桥梁钢筋锈蚀影响因素分布类型及参数

2.3 Kriging优化模型分析

优化Kriging模型时，粒子群优化算法参数设置为：粒子群数量设置为50个，最大迭代次数为300次，惯性权重为0.5，学习因子分别为1.5和2.5。经过300次迭代，得到的预测影响值与真实值间的误差曲线如图3所示，可以看出在50次迭代时找到最优Kriging相关性参数，误差从0.1降低至10-12，可以认为经过优化后的Kriging模型能够准确对训练样本进行计算。

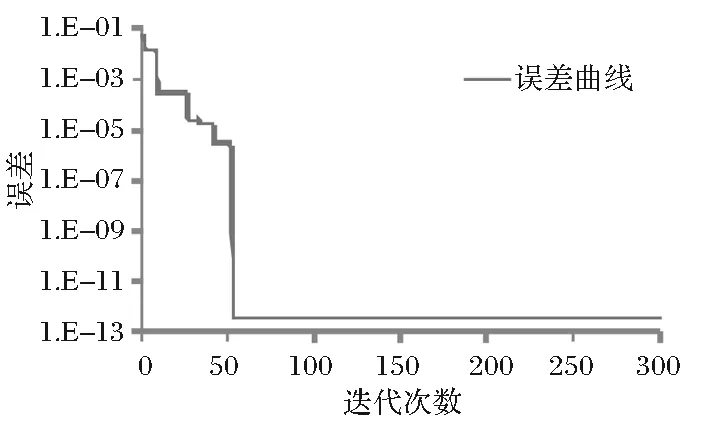
图3 粒子群算法优化Kriging模型误差曲线

利用优化的Kriging模型计算表1所示的影响因素条件下钢筋锈蚀程度及误差，如表3所示。并对五组未训练的样本数据进行预测，得到的结果如表4所示。

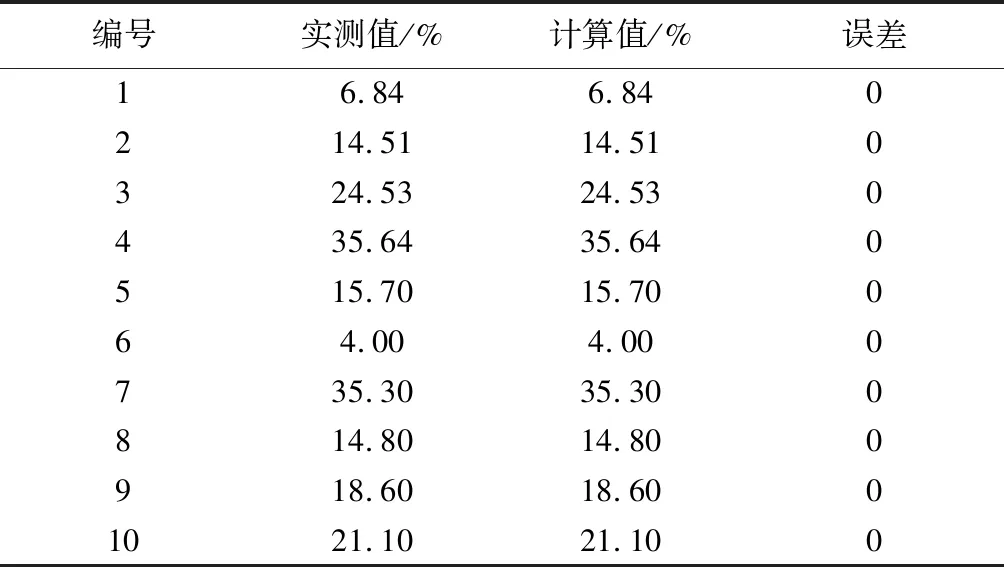
表3 训练样本数据响应计算值及误差

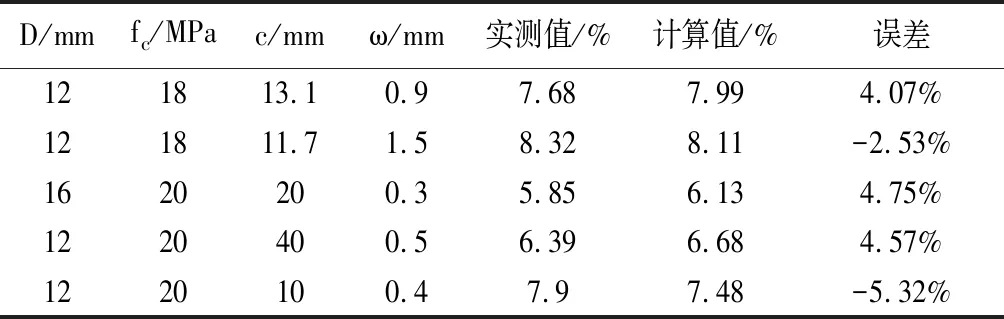
表4 非训练样本数据响应计算值及误差

从表3可以看出训练样本响应计算结果与真实结果吻合，说明经过优化的Kriging模型能够准确计算训练样本条件下的桥梁钢筋锈蚀程度。而从表4的结果可以看出，Kriging模型具有一定的预测能力，计算未经训练过的影响因素条件下钢筋锈蚀程度与实测值的误差在5%左右，表明预测结果可以用于桥梁钢筋锈蚀适用性可靠性分析。

3 桥梁钢筋锈蚀可靠度分析

3.1 桥梁钢筋锈蚀功能函数

文献[7]中对钢筋锈蚀率与钢筋屈服强度间的关系进行研究，钢筋的屈服强度、极限抗拉强度和延伸率随钢筋锈蚀程度的增加而逐渐减小，钢筋锈蚀程度小于10%时，仍有明显的屈服台阶，而大于20%时，钢筋屈服台阶基本丧失。因此，本文以20%作为钢筋适用性极限值来建立桥梁钢筋锈蚀功能函数，如式(11)所示。

z=20%-fKriging(D,fc,c,ω)

(11)

式中：fKriging为考虑钢筋直径、混凝土抗压强度、保护层厚度和沿筋方向裂缝宽度四种主要因素的Kriging预测钢筋锈蚀程度函数。

在对上式计算时，四种因素的分布类型及参数选用表2所示的分析结果，并采用Monte-Carlo方法[9]进行计算。得到的失效概率为0.24%，可靠度指标为2.81。

3.2 四种因素对桥梁钢筋锈蚀可靠度的影响分析

对所确定的四种主要钢筋锈蚀影响因素进行分析，计算单个因素均值变化而其他因素参数不变条件下的钢筋锈蚀可靠度，具体分析如下。

(1)钢筋直径

计算钢筋直径取值范围在10～30mm间变化时的钢筋锈蚀失效概率(Pf)和可靠度指标(β)，计算时其分布类型和标准差以及其他因素分布类型和参数如表2所示，计算结果如图4所示。

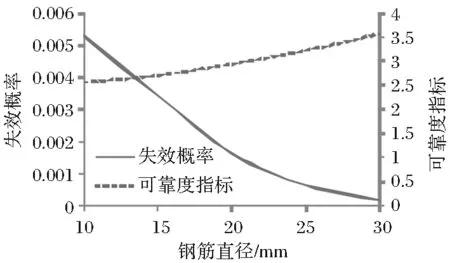
图4 Pf和β随钢筋直径变化曲线

从图4可以看出，随钢筋直径增加钢筋锈蚀Pf和β分别成线性降低和增加。表明在同等条件下，直径越大钢筋抵抗锈蚀的能力越强，可靠度越大。

(2)混凝土抗压强度

分析混凝土抗压强度对钢筋锈蚀Pf和β影响时，混凝土抗压强度控制在15～35MPa之间，其他因素同样控制不变，Pf和β变化曲线如图5所示。

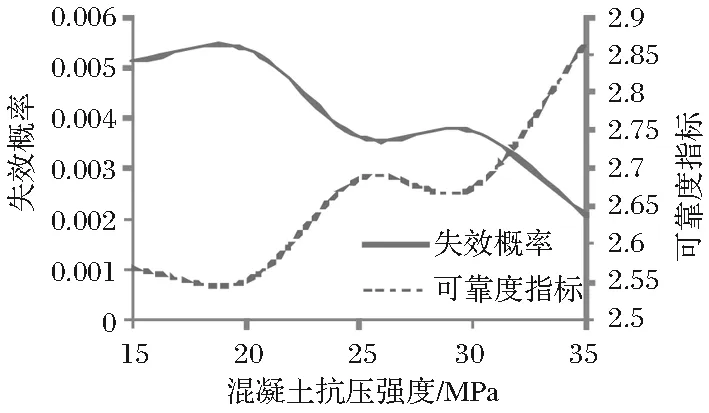
图5 Pf和β随混凝土抗压强度变化曲线

图5显示混凝土抗压强度对钢筋锈蚀Pf和β没有明显影响规律，Pf和β总体趋势是随着混凝土抗压强度的增加而降低，说明抗压强度越大对钢筋的保护能力越强，钢筋锈蚀的可能性越小。

(3)保护层厚度

分别计算了保护层厚度从20mm增加到40mm时的桥梁钢筋锈蚀Pf和β变化曲线如图6所示。

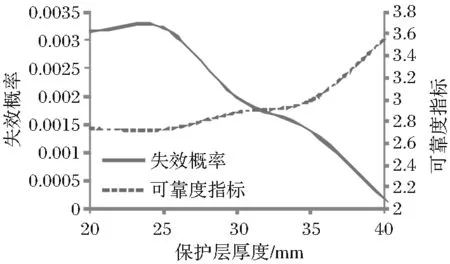
图6 Pf和β随保护层厚度变化曲线

当混凝土保护层厚度增大时，Pf线性降低；而β在抗压强度小于30MPa时上升幅度较小，当抗压强度大于30MPa时，β快速增加。表明混凝土保护层厚度越大，钢筋锈蚀程度大于20%的可能性越小。

(4)沿筋方向裂缝宽度

沿筋方向裂缝宽度取值确定在0.1mm到2.0mm，得到的钢筋锈蚀Pf和β变化曲线如图7所示。

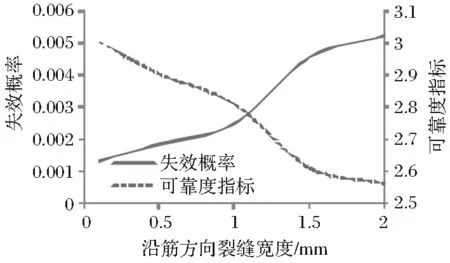
图7 Pf和β随沿筋方向裂缝宽度变化曲线

图7可以看出，随着沿筋方向裂缝宽度的增加，钢筋锈蚀Pf逐渐增大、β呈线性降低。当裂缝宽度大于1.5mm时，曲线变化趋势趋于平缓，说明随着裂缝宽度的增加，钢筋锈蚀程度大于20%的可能性越大。裂缝主要由钢筋锈胀引起，所以桥梁钢筋可靠度逐渐降低。

4 结论

利用粒子群算法优化Kriging模型以及Monte-Carlo方法，对桥梁钢筋锈蚀适用性可靠度进行了计算分析，得出以下结论：

(1)粒子群算法能够快速搜寻到最优相关性参数值，经过粒子群算法优化的Kriging模型具有较高的拟合精度。

(2)优化后的Kriging模型能够准确计算训练样本中钢筋锈蚀影响因素条件下的钢筋锈蚀程度，且对非训练样本数据具有一定的预测能力，能够用于可靠度分析计算中。

(3)四种因素对钢筋锈蚀可靠度的影响作用为：随着钢筋直径和保护层厚度增加，钢筋锈蚀可靠度线性增大；混凝土抗压强度对可靠度没有明显规律，但总体趋势也是随抗压强度的增大而增大；当裂缝宽度增大时，可靠度逐渐降低。因此，在实际工程中应定期对桥梁进行检测，根据实测数据进行可靠度分析，并根据可靠度进行养护方案的制定。