不同脱粘程度对钢管混凝土桁拱受力性能影响

陈津凯

(福建省交通建设工程试验检测有限公司 福建福州 350008)

0 引言

钢管混凝土作为一种受力性能优良的组合材料，被广泛运用于各种形式的结构中，但钢管与混凝土之间的界面粘结问题(即脱粘问题)是影响其组合性能的重要因素，尤其是在大跨度钢管混凝土拱桥中[1]。脱粘产生的原因，可归结为热脱粘、收缩脱粘、荷载引起的脱粘、施工工艺引起的脱粘等几种，其中热脱粘是主要原因且难以避免[2-3]。

关于脱粘对钢管混凝土拱桥受力性能的影响，已有了较多的研究，主要认为，脱粘对单圆管拱的影响较小，而对桁拱的影响比较大[4-5]。涂光亚等[6]认为脱粘对钢管混凝土桁拱的影响大于单圆管拱，主要表现为脱粘会明显减少桁拱的刚度和面内极限承载力，而对单圆管拱几乎没有影响。陈津凯[7]进行了脱粘对钢管混凝土桁拱受力性能影响的分析，认为脱粘对桁拱变形和承载力均有较大的影响，且脱粘出现后，桁拱变形增大，极限承载力减少。

上述有关脱粘对钢管混凝土桁拱影响的研究，都是考虑桁拱完全脱粘的特殊情况，而实际工程中并不会发生完全脱粘，发生脱粘的长度和位置情况不尽相同[8-9]。因此，探讨不同脱粘程度对桁拱受力性能的影响非常必要。

基于此，本文以某钢管混凝土拱桥为背景工程，建立考虑不同脱粘长度和不同脱粘位置的有限元模型，讨论两者对钢管混凝土桁拱力学性能的影响，分析结果拟为实际工程设计、旧桥承载能力评定提供参考。

1 背景工程概况

某钢管混凝土拱桥为飞鸟式桁式拱桥，主跨507m。主跨桁拱拱轴线为悬链线，拱轴系数m=1.5，净矢跨比为1/4，总体布置如图1所示。主跨桁拱采用等宽变高空间桁架结构，拱顶截面径向高为7.0m，拱脚截面径向高为14.0m，肋宽为4.0m，每肋为上、下各两根Φ1300mm×22mm、Φ1300mm×26mm、Φ1300mm×30mm的钢管混凝土弦杆，弦杆通过横联钢管Φ760mm×16mm和竖向两根腹杆Φ660mm×12mm钢管连接而成。桁拱钢材为Q345C钢，管内混凝土采用C70混凝土。

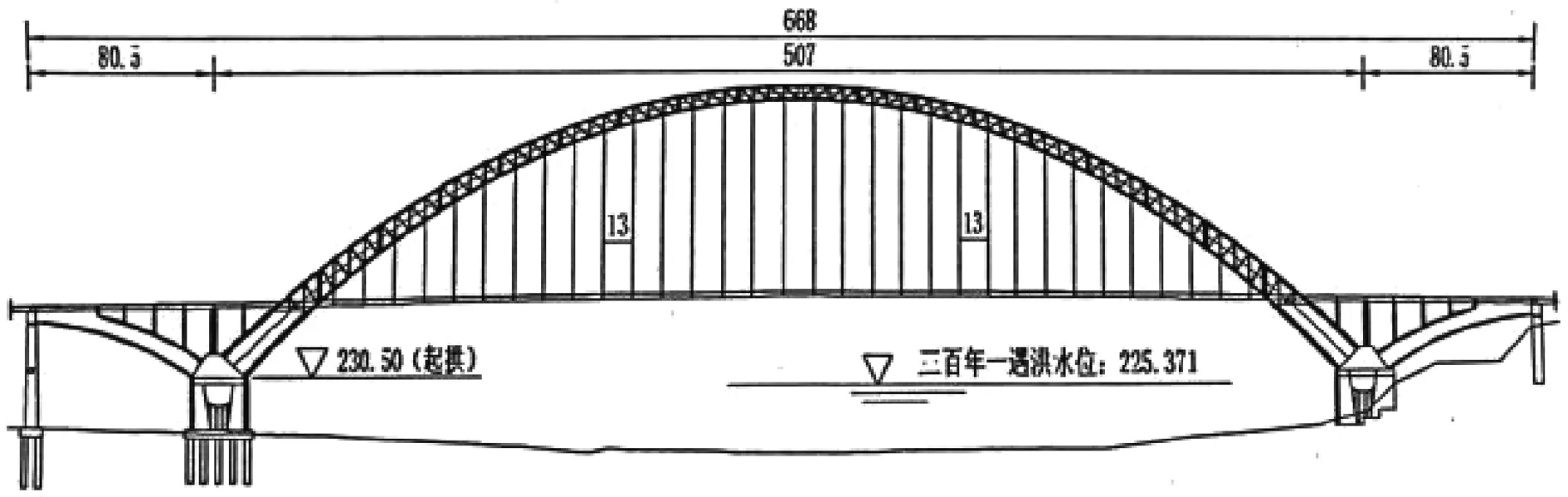
图1 某飞鸟式钢管混凝土拱桥总体布置图

2 具体研究方法

2.1 分析参数

脱粘长度和脱粘位置为本研究的主要分析参数。脱粘长度用Ld表示，其取值如图2(a)所示，以拱顶为中心，向两边拱脚对称延伸，考虑脱粘长度分别为0(完全粘结)、L/4、L/2、3L/4和L(完全脱粘)5种情况。脱粘位置的选取如图2(b)所示，考虑脱粘位置分别在桁拱两边拱脚、四分点及拱顶处5种情况，并取脱粘长度均为L/8。

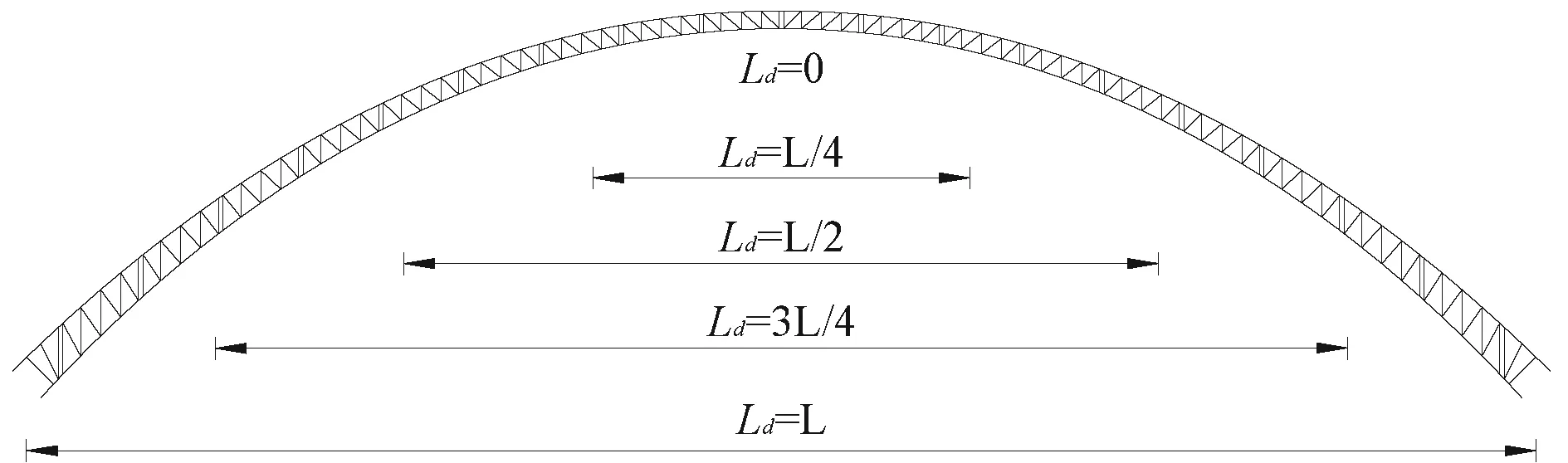
(a) 脱粘长度

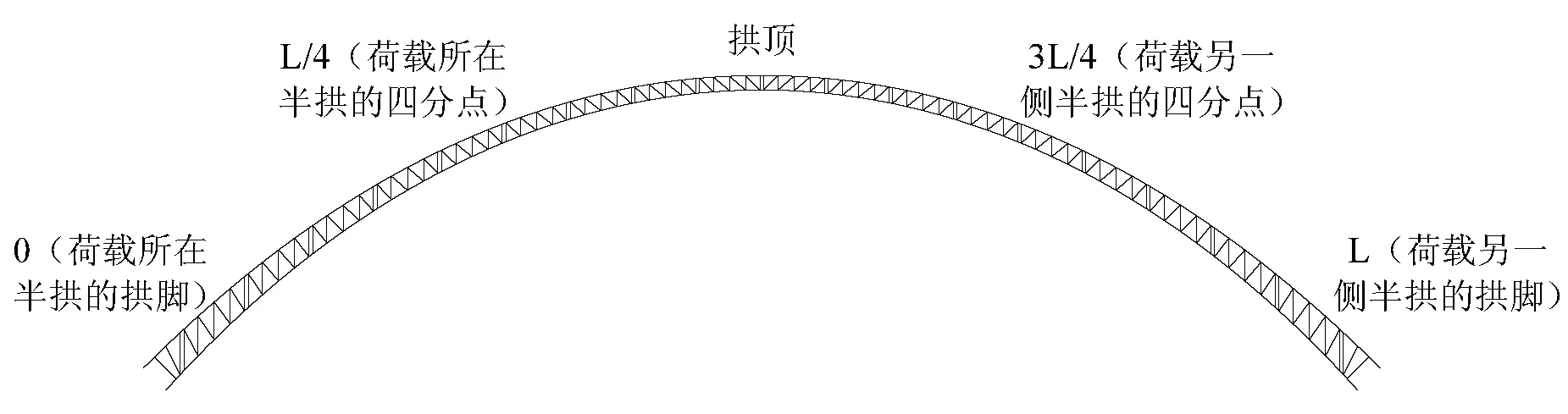
(b) 脱粘位置图2 脱粘长度和脱粘位置示意图

2.2 有限元模型建立

利用通用软件ABAQUS进行建模，模型中所有单元均为三维梁单元，采用非线性弹簧单元模拟钢管与核心混凝土的粘结滑移关系。由于是分析桁拱面内力学性能，故仅设置主管径向(垂直于钢管与混凝土界面)和主管轴向(平行于钢管与混凝土界面)的弹簧单元。对于完全粘结模型，沿桁拱轴向的弹簧单元本构关系采用文献[10]提出的钢管与混凝土间的粘结-滑移本构。对于完全脱粘模型，满足下述条件：①脱粘厚度为3mm；②桁拱全截面脱粘；③不考虑钢管与混凝土间的粘结滑移，即二者能自由滑动。

基于文献[11]对钢管混凝土桁拱所进行的受力性能试验，本研究以该试验模型A-0为分析对象，对桁拱有限元模型进行验证。图3为有限元计算结果与文献[11]的试验模型A-0荷载-挠度曲线。从图3中可以看出，有限元方法计算的结果与试验结果吻合较好，可以用于钢管混凝土桁拱受力性能的分析。

混凝土采用文献[12]提出的考虑了套箍系数ζ影响的核心混凝土应力-应变关系曲线，如式(1)所示：

(1)

式中相关参数意义及计算方法参见文献[12]。

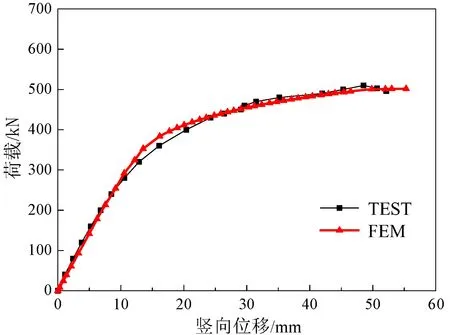
(a)跨中截面

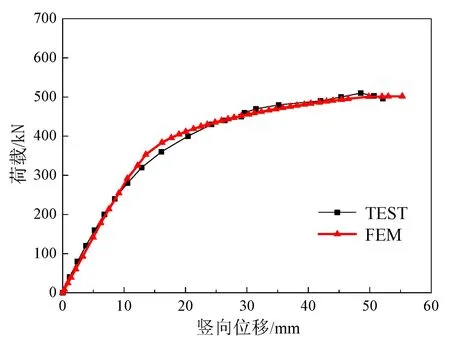
(b)L/4截面图3 有限元计算结果与试验模型A-0荷载-挠度曲线的对比

钢材本构采用五线段模型，如图4所示。Es为钢材弹性模量；fps、fys和fus分别为比例极限、屈服强度和抗拉强度；εe=fps/Es，εe1=1.5εe，εe2=10εe1，εe3=100εe1，fps=0.8fys。

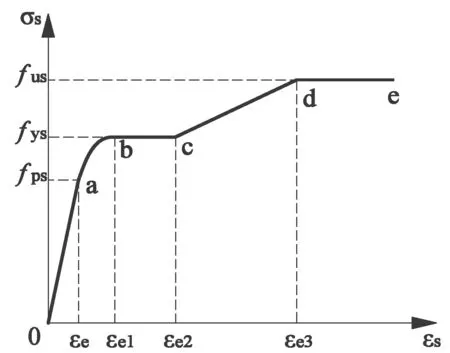
图4 钢材应力-应变曲线

文献[6-7]进行了4种荷载工况下的脱粘影响分析，分别为跨中集中力、L/4处集中力、全跨均布荷载和半跨均布荷载。其分析结果表明，非对称荷载作用(L/4处集中力和半跨均布荷载)下脱粘的影响程度更大，且半跨均布荷载作用的影响最大。因此，本研究取半跨均布荷载工况进行分析，并取均布荷载为100kN/m。

3 计算结果分析

3.1 内力

桁拱的内力主要为轴力和弯矩，而弯矩又是通过上下弦管的轴力差形成的。因此，本研究主要以弦管所受轴力的变化来说明不同脱粘程度对桁拱的影响。

不同脱粘长度时的桁拱拱脚下弦轴力与完全粘结时轴力的比值列于表1，受压为正，受拉为负。

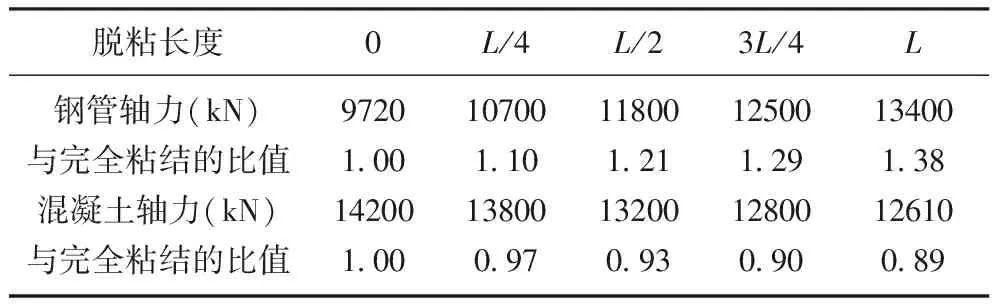
表1 不同脱粘长度时桁拱拱脚下弦轴力

从表1可以看出，脱粘使得钢管轴力增大，核心混凝土轴力减少，表明脱粘破坏了钢管与混凝土之间的协同受力作用，使得弦杆钢管加载，而核心混凝土卸载。

基于钢管加载是不利的，因此，为分析钢管加载程度，表2～表3仅列出桁拱上弦和下弦钢管的轴力。由表中可以看出，对于上弦钢管，最大轴力比完全粘结时增大了27%；对于下弦钢管，最大轴力比完全粘结时增大了38%。

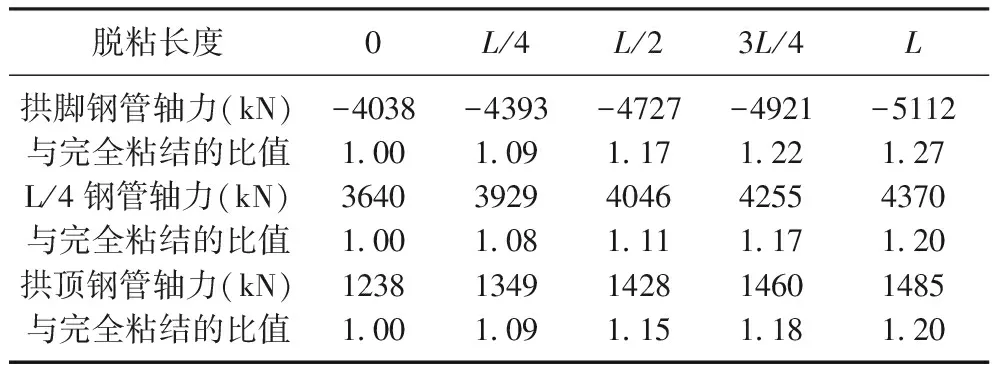
表2 不同脱粘长度时桁拱上弦轴力

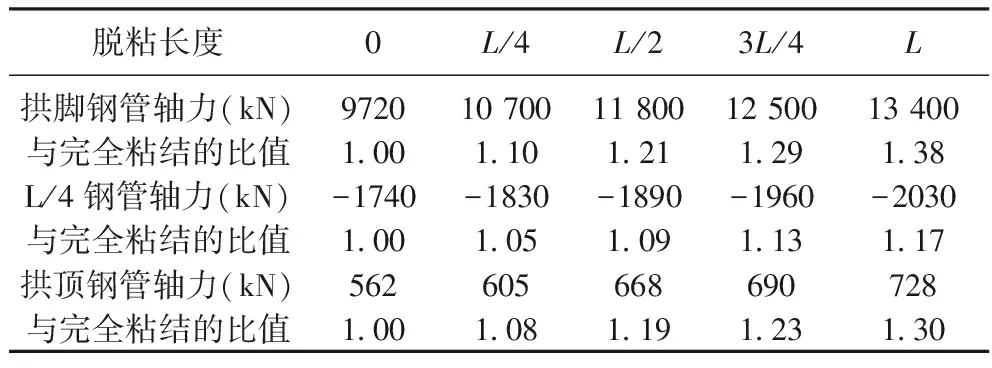
表3 不同脱粘长度时桁拱下弦轴力

表4～表5列出不同位置脱粘时桁拱上弦和下弦钢管的轴力(脱粘长度均为L/8)。其中，0和L/4分别表示荷载所在半拱的拱脚和四分点出现脱粘，L/2表示拱顶出现脱粘，3L/4和L分别表示未布置荷载半拱的四分点和拱脚出现脱粘。由表中可以看出，无论桁拱上弦或下弦，脱粘所在位置的影响明显大于未脱粘的截面，因此，脱粘处钢管的应力是工程实践中关注的重点。

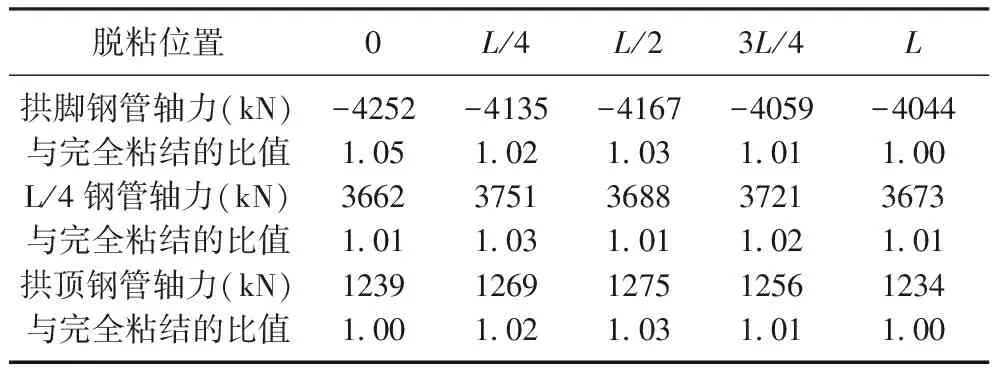
表4 不同脱粘位置时桁拱上弦轴力

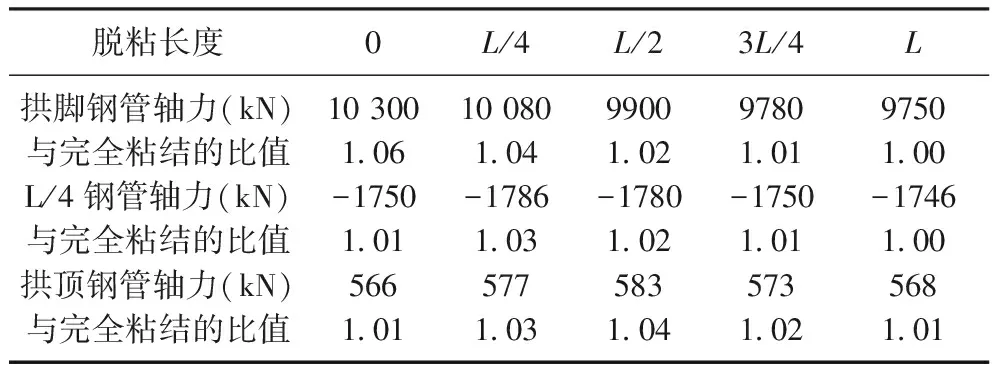
表5 不同脱粘位置时桁拱下弦轴力

3.2 变形

图5为半跨均布荷载作用下，不同脱粘长度时桁拱的竖向位移。由图5可以看出，随着脱粘长度的增大，桁拱的竖向位移也不断增大。

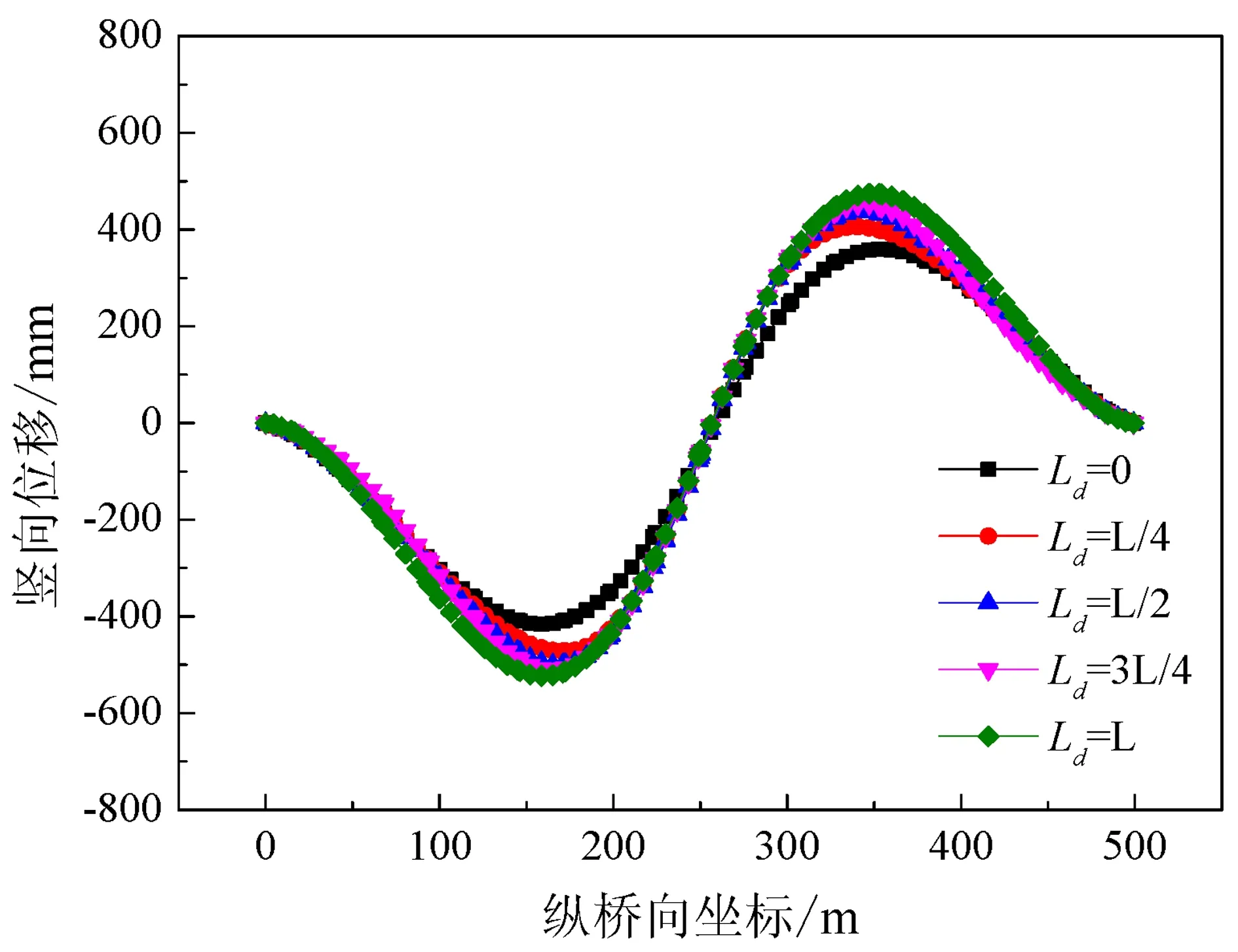
图5 不同脱粘长度对桁拱竖向位移的影响

最大竖向位移为L/4截面处，桁拱的最大挠度列于表6。由表6可以看出，当脱粘长度从0增加到L/4时，最大挠度增幅较大，为14%；从L/4增加到L/2时，最大挠度增幅较小，为6%；之后，当脱粘长度从L/2增加到L时，最大挠度基本线性增加。与完全粘结时相比，脱粘长度为L(完全脱粘)时的最大挠度增大了26%。

表6 不同脱粘长度时桁拱的最大挠度

图6为半跨均布荷载作用下，不同位置出现L/8长度脱粘时桁拱的竖向位移。由图6可以看出，该参数变化对桁拱的竖向位移影响不大。

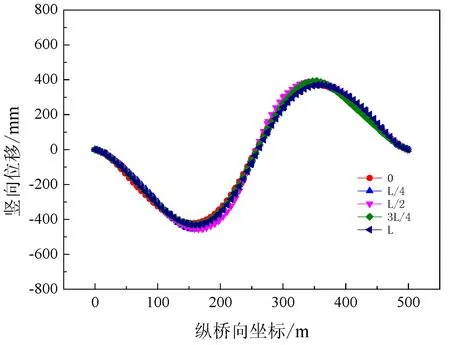
图6 不同脱粘位置对桁拱竖向位移的影响

3.3 极限承载力

表7为不同脱粘长度时桁拱的极限承载力与完全粘结时桁拱极限承载力的比值。由图7可以看出，当脱粘长度从0增加到L/2时，极限承载力降低幅度较大，约为15%；之后，当脱粘长度从3L/2增加到L时，极限承载力降幅相对较慢，为9%。与完全粘结时相比，脱粘长度为L时，其极限承载力降低了24%。

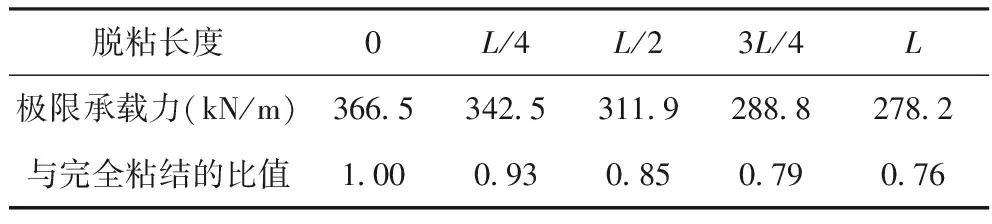
表7 不同脱粘长度时桁拱的极限承载力

表8为不同脱粘位置时极限承载力与完全粘结时极限承载力的比值。由表8可以看出，当桁拱不同位置出现脱粘长度L/8后，极限承载力降低，但幅度很小，不超过3%。在半跨均布荷载作用下，当桁拱脱粘位置位于荷载所在半拱一侧的拱脚时，脱粘对桁拱极限承载力的影响相对较大。

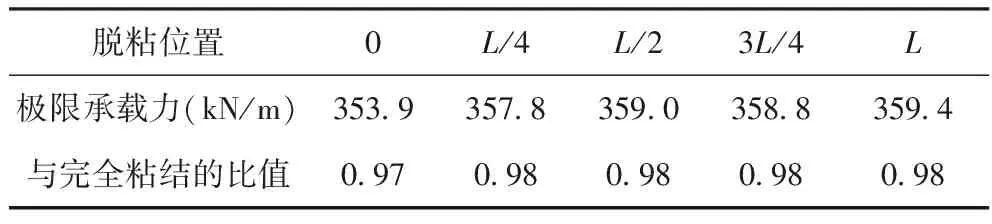
表8 不同脱粘位置时桁拱的极限承载力

4 结论

(1)钢管混凝土桁拱脱粘，破坏了钢管与混凝土之间的协同受力作用，使得弦杆钢管加载，而核心混凝土卸载。对于上弦和下弦钢管，最大轴力比完全粘结时分别增大了27%和38%。

(2)无论桁拱上弦或下弦，脱粘所在位置影响明显大于未脱粘的截面，脱粘处钢管的应力是工程实践中关注的重点。

(3)脱粘长度越大，桁拱最大挠度也越大。当脱粘长度从0增加到L/4时，最大挠度增幅较大，为14%；从L/4增加到L/2时，最大挠度增幅较小，为6%；之后，当脱粘长度从L/2增加到L时，最大挠度基本线性增加。与完全粘结时相比，脱粘长度为L(完全脱粘)时的最大挠度增大了26%。脱粘位置(脱粘长度为L/8)的变化对桁拱的竖向位移影响不大。

(4)脱粘长度增大，桁拱极限承载力降低。当脱粘长度从0增加到L/2时，极限承载力降低幅度较大，约为15%；之后，当脱粘长度从3L/2增加到L时，极限承载力降幅相对较慢，为9%。与完全粘结时相比，脱粘长度为L时，其极限承载力降低了24%。

(5)桁拱不同位置出现脱粘长度L/8后，极限承载力小幅降低，不超过3%。在半跨均布荷载作用下，当桁拱脱粘位置位于荷载所在半拱一侧的拱脚时，脱粘对桁拱极限承载力的影响相对较大。