跳频序列集的时频二维部分汉明相关理论界
2019-09-06许成谦
许成谦, 李 鑫
(1. 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004; 2. 燕山大学 河北省信息传输与信号处理重点实验室, 河北 秦皇岛 066004)
0 引言
跳频多址通信技术广泛应用在现代通信系统中[1]。跳频扩频系统的重要问题是在可供跳频的载频上的跳频序列具有好的汉明相关性。 相对于传统的周期汉明相关性,跳频序列的部分汉明相关性更具有一般性。对于跳频序列只含有时延的一维部分汉明相关性理论界的研究取得了很多成果[2-4]。当通信终端高速移动时,多普勒现象会导致频移,这样考虑跳频序列既有时延又有频移的二维汉明相关性具有重要的意义。目前对于跳频序列的二维汉明相关性的研究还比较少。文献[5]给出了无碰撞区跳频序列时频二维周期汉明相关的理论界。文献[6]给出了低碰撞区跳频序列时频二维周期汉明相关的理论界。 文献[7]构造出了满足时频二维周期汉明相关理论界低碰撞区跳频序列集。 文献[8-9]依据理论界对几类跳频序列集的时频二维周期汉明相关值进行了分析。
本文着重研究跳频序列和序列集时频二维部分汉明相关理论界,给出了跳频序列时频二维部分汉明自相关、互相关的概念,证明了跳频序列集时频二维部分汉明自相关、互相关所满足的理论界。
1 相关概念
设F是频隙集合,周期为N的序列x=(x0,x1,…,xN-1),xi∈F,i=0,1,…,N-1,称为F上的跳频序列[10]。F上的不同跳频序列组成的集合称为跳频序列集。
设Zq为q阶加法整数群。 对于Zq上任意两个周期为N的跳频序列,x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1),0≤τ≤N-1,ω∈Zq,称
(1)
为跳频序列x和y的时频二维周期汉明互相关函数。其中,当xi=yi时,h(xi,yi)=1,当xi≠yi时,h(xi,yi)=0。τ表示相对时延,ω表示频移,且i+τ≡(i+τ)modN,i=0,1,…,N-1。当x和y相等时,Hxy(τ,ω)被称为时频二维周期汉明自相关函数,记为Hxx(τ,ω)。
定义1 设x=(x0,x1,…,xN-1)和y=(y0,y1,…,yN-1)为Zq上两个周期为N的跳频序列,若对于0≤τ,t (2) 则称Hxy(τ,ω;t|L)为跳频序列x和y起点为t、相关窗长度为L时频二维部分汉明互相关函数。当x和y相等时,Hxy(τ,ω;t|L)为跳频序列x和y的时频二维部分汉明自相关函数。 若t=0,L=N时,时频二维部分汉明相关函数退化为时频二维周期汉明互相关函数,这时Hxy(τ,ω;t|L)记为Hxy(τ,ω)。 本文中,用 表示跳频序列集S的最大时频二维部分汉明自相关。 用 表示跳频序列集S的最大时频二维部分汉明互相关。当t=0,L=N时,Pa(S)和Pc(S)分别退化为跳频序列集S的最大时频二维周期汉明自相关和最大时频二维周期汉明互相关,分别记为Ha(S)和Hc(S)。 在不引起混淆的情况下记Pa(S)=Pa,Pc(S)=Pc。 引理1 设F为q阶加法群频率集合。S是由F上M个周期为N跳频序列组成的集合,则跳频序列集总的时频二维周期汉明相关值 证明在文献[6]的引理6中,取Z1=N-1,Z2=q-1即可以得到结论。证毕。 给定一个跳频序列集S,对于任意窗长度L,0 引理2 设S是频隙数为q,序列长度为N的M个跳频序列组成的序列集S,Pa和Pc分别为跳频序列集S的最大时频二维部分汉明自相关和最大时频二维部分汉明互相关,对于任意整数L,0 P(L)≤ML+M(Nq-1)Pa+M(M-1)NqPc。 证明对于x,y∈S,由定义1知, 因此 ML+M(Nq-1)Pa+M(M-1)NqPc,证毕。 引理3[11]对于任意正整数τ,τ=0,1,…,N-1,有 推论1 对于任意正整数t,τ,L,且t,τ=0,1,…,N-1,L=1,2,…,N,有 证明设 因为跳频序列是周期为N的序列,所以bN+τ=bτ,bN+τ+1=bτ+1,…,bN+τ+L-2=bτ+L-2。 这样有 又因为 证明对于任意i=1,2,…,M,τ=0,1,…,L-1,ω=0,1,…,q-1,t=0,1,…,N-1,L=1,2,…,N,因为 所以 由文献[11]中引理3的证明可知 所以 证毕。 令函数 m(bk+τ+ω,fi), (3) 证明令 uk=m(bk,fi),vk=m(b(k)+ω,fi), 其中,k=t,t+1,…,t+L-1,0≤t≤N-1,则由式(3)得 引理5 设频隙集合F={f0,f1,…,fq-1},S是由F上M个周期为N的跳频序列组成的集合,x∈S,y∈S,对于任意正整数t,L,0≤t≤N-1,1≤L≤N,则P(L)≥M2NL。 证明由推论3知 由推论1知 再应用引理4得 定理1 设频隙集合F={f0,f1,…,fq-1},S是由F上M个周期为N的跳频序列组成的集合,Pa是最大时频二维部分汉明自相关,Pc是最大时频二维最大部分汉明互相关,则对于任意正整数t,L,0≤t≤N-1,1≤L≤N,有 (Nq-1)Pa+(M-1)NqPc≥MNL-L。 证明由引理2和引理5可得 M2NL≤P(L)≤ML+ M(Nq-1)Pa+M(M-1)NqPc, 则(Nq-1)Pa+(M-1)NqPc≥MNL-L,证毕。 设S是由Zq上M个周期为N的跳频序列组成的集合,相关窗长度为L,起点为t,1≤L≤N,0≤t≤N-1,用 表示跳频序列集S的总的时频二维部分汉明自相关函数。用 表示跳频序列集S的总的时频二维部分汉明互相关函数。用 表示跳频序列集S的平均时频二维部分汉明自相关函数。用 表示跳频序列集S的平均时频二维部分汉明互相关函数。 定理2设S是由Zq上M个周期为N的跳频序列组成的集合,相关窗长度为L,起点为t,1≤L≤N,0≤t≤N-1,则有 (4) 证明 Ra(S;L)+2Rc(S;L)= 由引理1知 则 Ra(S;L)+2Rc(S;L)≥N2M2L-MNL, 又因为 所以 使得定理2中不等式(4)成立的跳频序列集S称为最优平均时频二维部分汉明相关性跳频序列集。 用Hxy(τ,ω;t|L)替换文献[6]定义2中的H(xy)(l,v)得到的区间[0,LHt]×[0,LHf]、[0,LAHt]×[0,LAHf]、[0,LCHt]×[0,LCHf]分别为跳频序列集S的时频二维部分汉明相关低碰撞区、时频二维部分汉明自相关低碰撞区、时频二维部分汉明互相关低碰撞区。 对于任意正整数Z1,Z2,0≤Z1≤LHt,0≤Z2≤LHf,用 表示低碰撞区跳频序列集S的时频二维总部分汉明自相关函数。 用 表示低碰撞区跳频序列集S的时频二维总部分汉明互相关函数。 用 表示低碰撞区跳频序列集S的平均时频二维部分汉明自相关函数。 用 表示低碰撞区跳频序列集S的平均时频二维部分汉明互相关函数。 (5) 证明对于0≤Z1≤LHt,0 由文献[6]中引理6可知 即 所以 整理可以得出结论中的不等式,证毕。 推论3在定理3条件下,有 (6) 将跳频序列的一维部分汉明相关函数扩展到时频二维部分汉明相关函数,在提出跳频序列的时频二维部分汉明自相关、时频二维部分汉明互相关、平均时频二维部分汉明自相关、平均时频二维部分汉明互相关等概念基础上,证明了跳频序列集时频二维部分汉明相关、平均时频二维部分汉明相关满足的理论界,证明了低碰撞区跳频序列集平均时频二维部分汉明相关满足的理论界。2 时频二维部分汉明相关性的理论界
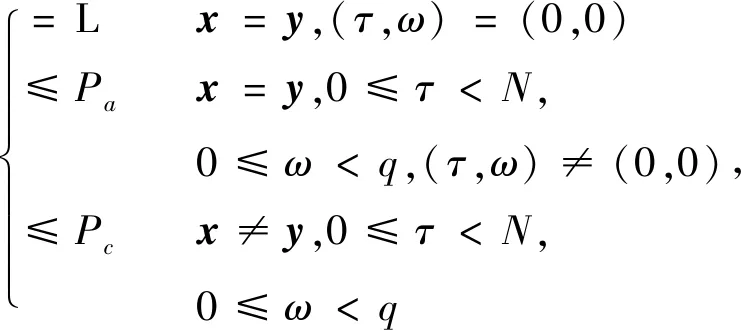


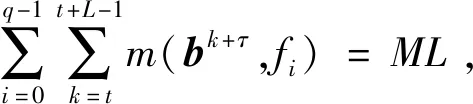
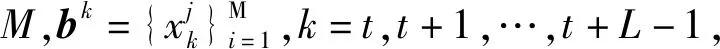



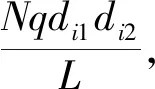
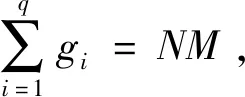
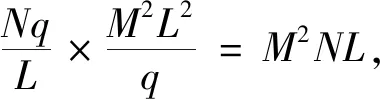
3 平均时频二维部分汉明相关理论界

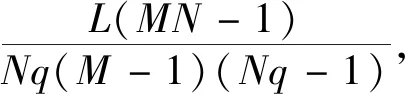
4 低碰撞区跳频序列集的平均时频二维部分汉明相关性的理论界

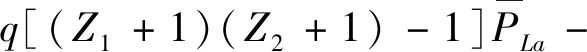

5 结论
