基于正交试验、组合赋权-灰色关联度法研究隧道施工最优方案*

吴 波，路 明，雷 领，黄 惟，兰扬斌

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004； 3.中交路桥建设有限公司，北京 101116)

0 引言

近些年来，我国城市地铁快速发展，建设数量和建设里程逐年增加，并取得巨大成就。城市地铁浅埋暗挖大断面隧道，因其跨度大，施工工序复杂，对围岩造成多次扰动，地表沉降难以控制，施工难度大[1]。合理选择施工方案是隧道顺利竣工的前提，针对影响浅埋暗挖大断面隧道的稳定性因素，调整隧道施工参数，以保证隧道施工过程中的稳定性。

大多学者采用数值模拟、模型试验、理论研究和现场监测数据等方法研究影响隧道稳定性的因素。来弘鹏等[2]采用现场试验研究加固区范围及其参数对隧道稳定性的影响规律；汪波等[3]采用数值模拟和现场试验等手段研究隧道加固方式和加固参数对砂性土浅埋暗挖隧道的影响；刘泉声等[4]采用模型试验和数值模拟手段研究隧道开挖顺序对隧道稳定性的影响，从而提出了特大断面浅埋暗挖隧道十字岩柱开挖技术；黄鑫等[5]采用数值模拟研究隧道埋深、隧道形状和侧压力系数对隧道施工的影响；吴波等[6-7]基于控制理论和动态规划原理，以地表沉降作为评价指标研究开挖工序对隧道稳定性的影响规律，但只用地表沉降作为稳定性评价指标，说服力不足；李梓源等[8]建立了由围岩等级、开挖尺寸等9个指标组成的多因素模型，采用灰色关联度对隧道稳定性进行评价，但评价指标的计算权重是1/n，意味着每个评价指标一样重要，并不符合实际情况；李术才等[9]采用熵值法对灰色关联度进行改进，建立了隧道坍塌风险评估模型，但权重计算时定性分析和定量分析未充分结合，具有一定的局限性。

上述的学者大多研究对象和评价指标单一，权重计算过程中很难符合实际情况。灰色关联度法评价指标权重为1/n，意味着各评价指标同样重要；熵值法—灰色关联度法在样本较少，且各样本差距不明显时，熵值法的各评价指标权重无明显差异，具有一定的局限性。

本文根据影响隧道稳定性的因素，构建L16(5×4)正交表进行正交试验，把地表沉降、围岩应力、右侧导洞拱顶沉降、初支剪应力作为评判指标，用熵值法[10]和层次分析法[11]进行组合赋权，将定性分析和定量分析有效结合，增强其准确性和客观性，特别在样本数量和差距均较小时，更能凸显各样本的优劣，从而选择最优方案。

1 组合赋权-灰色关联度评价法

1.1 灰色关联度分析法

灰色关联度分析法[12-13]是将研究对象及影响因素的因子值视为1条线上的点，与待识别对象及影响因素的因子值所绘制的曲线比较它们之间的贴近度，计算研究对象与待识别对象各影响因素之间的贴近程度的关联度，通过比较各关联度的大小来判断待识别对象对研究对象的影响程度。

1)评价指标矩阵

按照灰色关联度分析法，假设评价系统中有m个评价指标，n个试验方案，则评价指标矩阵A为：

(1)

2)对指标矩阵归一化

在系统的各评价指标中，采用越小越优的指标，对指标矩阵进行归一化，见式(2)：

(2)

式中：rij为特征矩阵R的特征向量，i=1,2,…,n；j=1,2,…,m。

根据式(2)处理后，矩阵A变为：

(3)

3)关联系数矩阵计算

各指标中的最大值作为参考方案，参考方案矩阵为：K=[k1k2…km]，其中kj=max(r1j,r2j,…,rnj)，j=1,2,…,m。

(4)

其中:

(5)

(6)

式(4)中分辨系数ρ∈[0,1]，本文中取0.5，经过式(4)～(6)处理后得到关联系数矩阵ζ：

(7)

1.2 组合赋权方法

权重赋值的方法一般有2种：主观赋权法和客观赋权法。客观赋权法采用熵值法，在信息论中，某项指标携带的信息量越大，说明该项指标对方案的决策作用越大，所以熵值法是通过计算各项指标值的变异程度来计算权重的。

1)熵值法

对指标矩阵A进行归一化处理:

(8)

各指标的信息熵：

(9)

熵值法权重：

(10)

2)主观赋值法

本文采用层次分析法计算主观权重βj，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。结果的影响程度都是量化的，清晰明确。

3)组合权重

本文将按照文献[14]中的组合权重进行计算，具体如式(11)所示：

(11)

4)理想方案的关联度计算

γ=ζω

(12)

式中：ω为组合权系数矩阵；γ为目标函数关联度矩阵。

2 工程实例

本文依托北京地铁17号线天通苑站歇甲村出入段线南肢项目，矿山法暗挖隧道里程为RDKO+138～RDKO+421，暗挖长度283 m(单洞双线283 m，分线桩号为RDK0+421)，隧道平面示意图如图1所示。

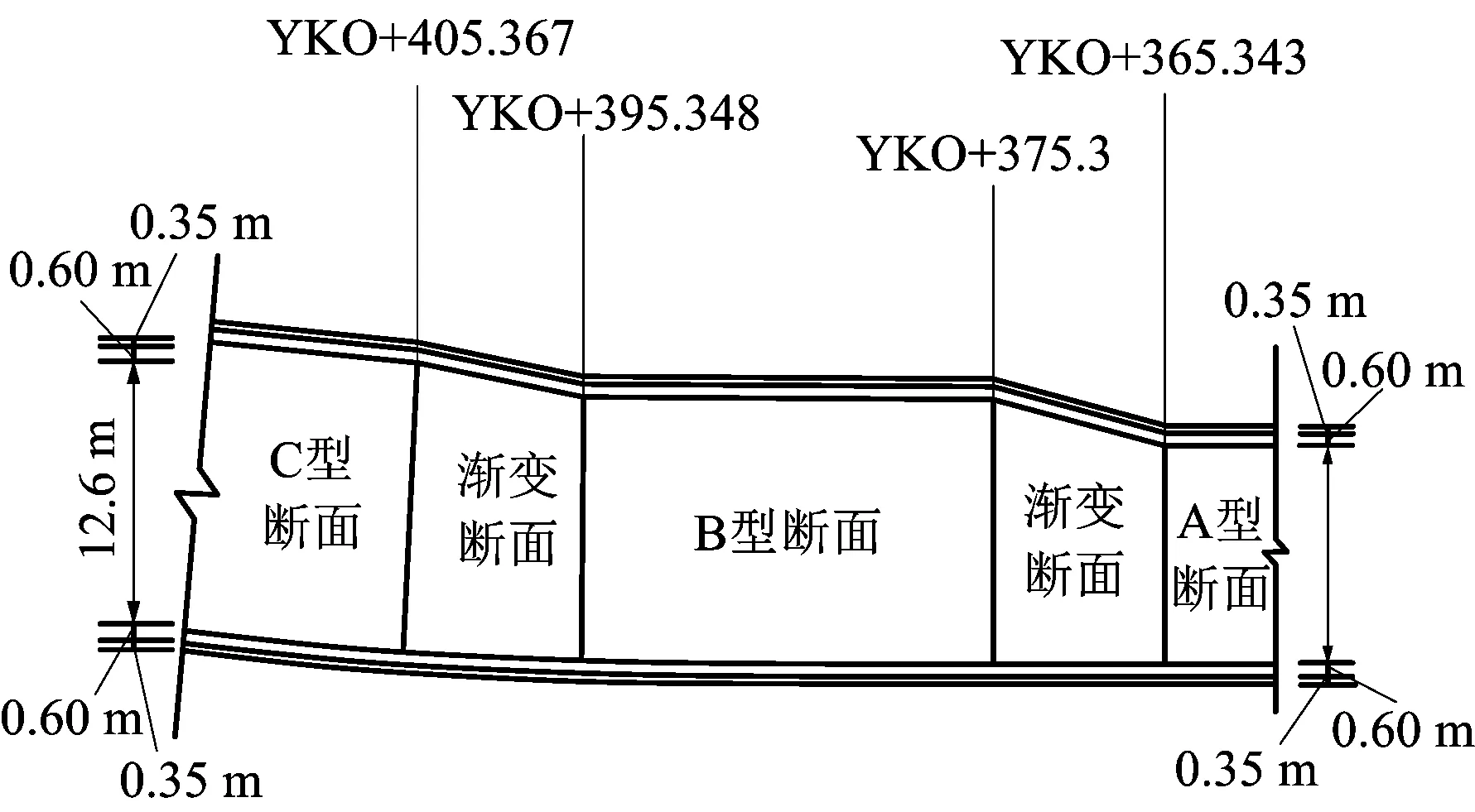
图1 渐变隧道平面示意Fig.1 Plane plan of gradient tunnel

本文原始方案采用动态分区法(Dynamic partition method简称DPM)，将隧道分为2个部分，Ⅰ为固定分区部分，隧道跨度固定为10 m，固定分区分为4个小导洞，分别为Ⅰ-1，Ⅰ-2,Ⅰ-3,Ⅰ-4部，采用CRD工法施工；Ⅱ为动态分区部分，能随隧道轮廓线增大而增大，从而实现隧道渐变。为了满足本工程的需求，i最大为4.5 m，最小为2.3 m，动态分区分为2个小导洞，分别为Ⅱ-5，Ⅱ-6部，采用台阶法施工。但是Ⅰ，Ⅱ部之间错开距离仍需讨论。DPM动态分区如图2～3所示。

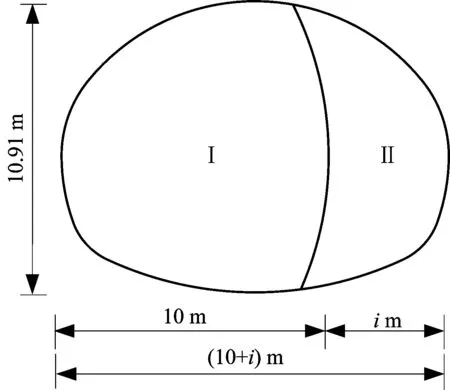
图2 动态分区法示意Fig.2 Schematic diagram of dynamic partitioning method

2.1 原始方案数值模型计算

对北京地铁17号线渐变大隧道原始方案进行数值分析，选取歇甲村出入段线南肢暗挖隧道断面面积最大的C段，跨度为14.5 m，高为10.91 m，埋深为7.5 m。围岩级别为Ⅵ级，模型X方向120 m，Y方向60 m，Z方向47 m，数值模型见图3。

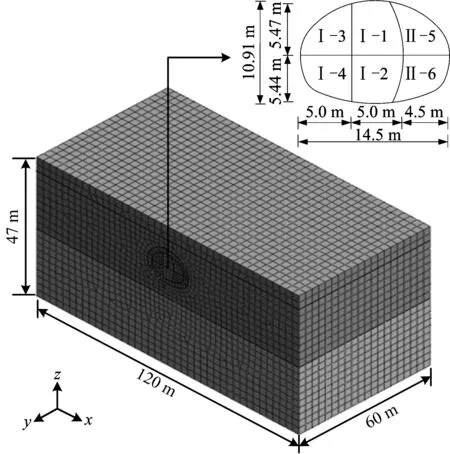
图3 数值计算模型Fig.3 numerical calculation model

围岩采用实体单元模拟，初期支护采用植入式梁单元模拟，通过提高加固区围岩的参数来模拟超前支护作用。根据新奥法的原理，二次衬砌作为安全储备，因此模型不考虑二次衬砌的影响，材料参数见表1。

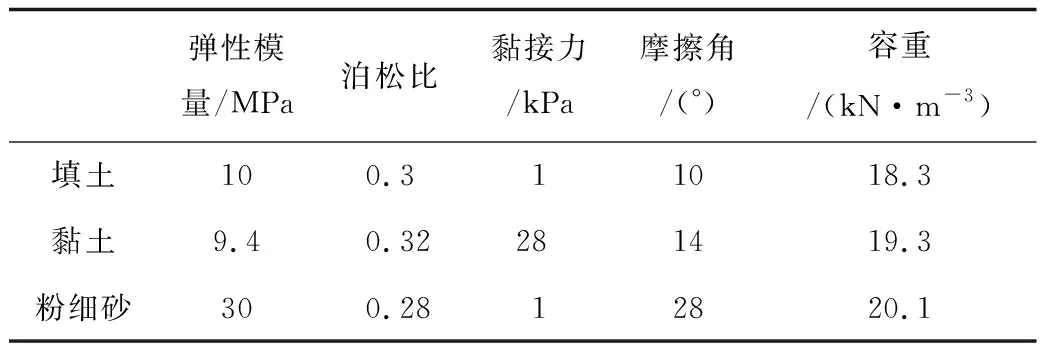
表1 材料参数Table 1 Parameters of materials

原始方案结果如表2所示，但施工步距、加固区强度及范围Ⅰ,Ⅱ部导洞错开距离以及施工工序是否是本工程的最优方案，是本文的重点研究内容。

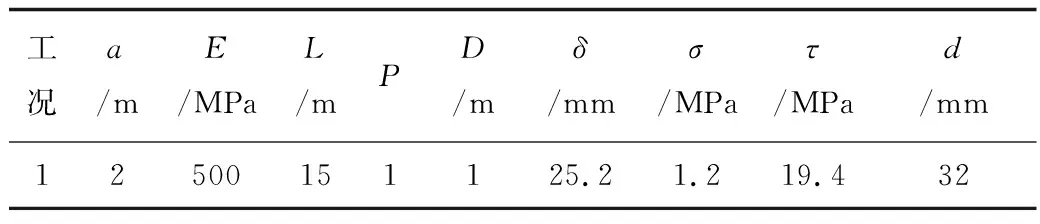
表2 隧道原始施工方案与结果Table 2 Original construction scheme and results of tunnel

注：a为施工步距;E为加固区强度;L为Ⅰ,Ⅱ部导洞错开距离;P为施工工序;D为加固区范围;δ为最大地表沉降;σ为围岩最大应力;τ为初支剪应力;d为右侧导洞拱顶沉降。

从文献[2-3]可知隧道加固范围和参数对隧道稳定性影响较大，本文隧道加固方式采用全断面灌浆加固，故将隧道全断面加固区的范围和参数为试验因素；从文献[6-8]可知隧道施工工序对隧道的稳定性影响很大，因此隧道施工工序是设计因素之一；施工步距影响初支是否能快速封闭成环，故把施工步距作为设计因素之一。施工工序不同即导致的施工顺序不同，施工工序如下：P1：1-2-3-4-5-6；P2：3-4-1-2-5-6；P3：5-6-1-2-3-4；P4：5-6-3-4-1-2。

2.2正交试验设计

在同一埋深和地质条件下，影响城市地铁浅埋暗挖大断面渐变隧道稳定性因素较多，本文通过广泛调研，认为施工工序、施工步距、加固区范围、强度以及Ⅰ，Ⅱ部导洞错开的距离等都能影响暗挖隧道稳定性，因此设计L16(5×4)正交表进行正交试验设计[15-16]，见表3。

表3 主要影响因素及水平Table 3 Main Influencing Factors and Levels

2.3 试验方案与结果

表4 为正交试验方案和结果。由表4可知，工况2的地表沉降最小为22.9 mm；工况1的围岩应力最小为0.78 MPa；工况1的喷混剪应力最小为6.6 MPa；工况5的右侧拱顶沉降最小为27.4 mm。P1和P2的整体结果均偏小，加固区范围0.5 m和强度500 MPa的计算结果均偏大。

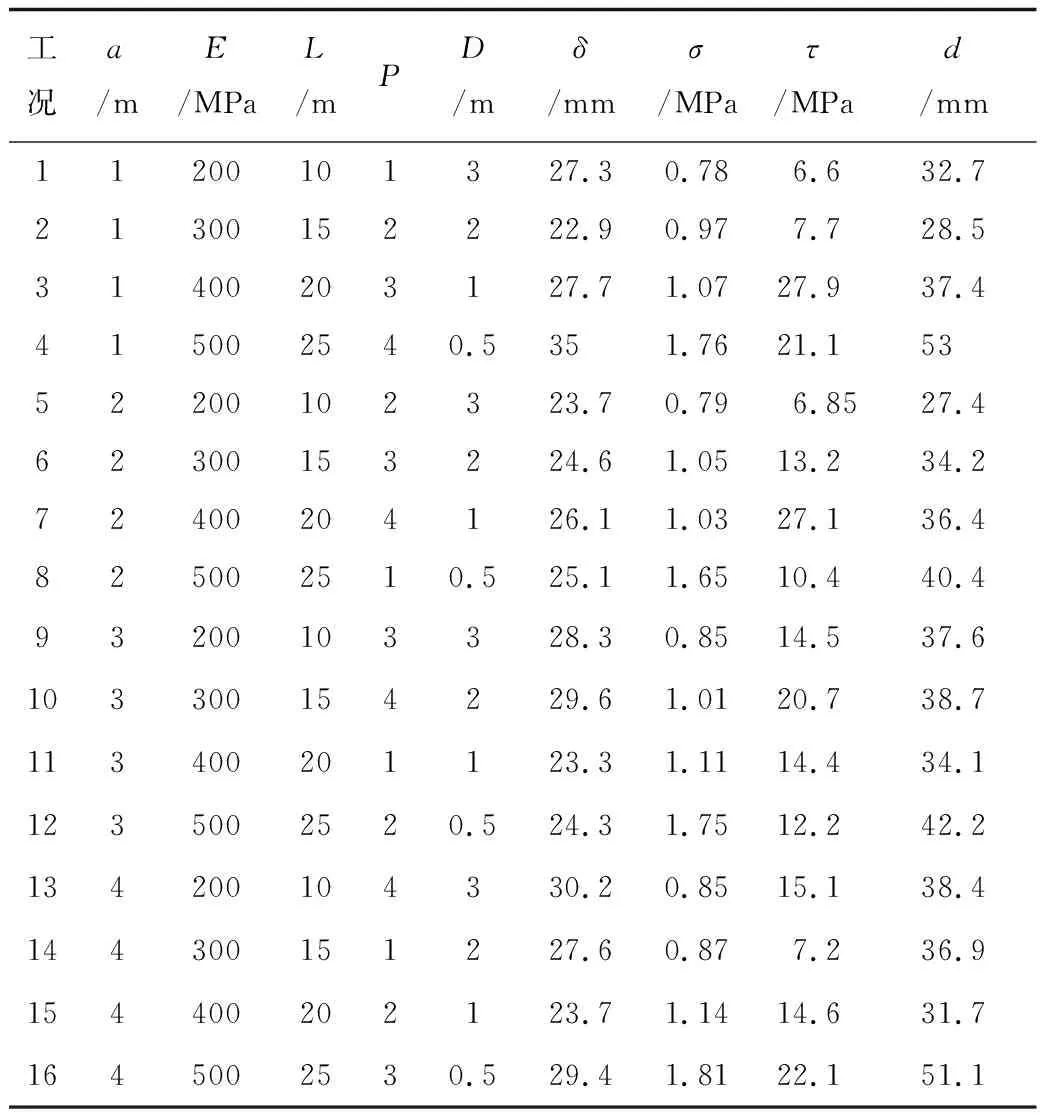
表4 正交试验方案和结果Table 4 Orthogonal test protocol and results

2.4 数据处理

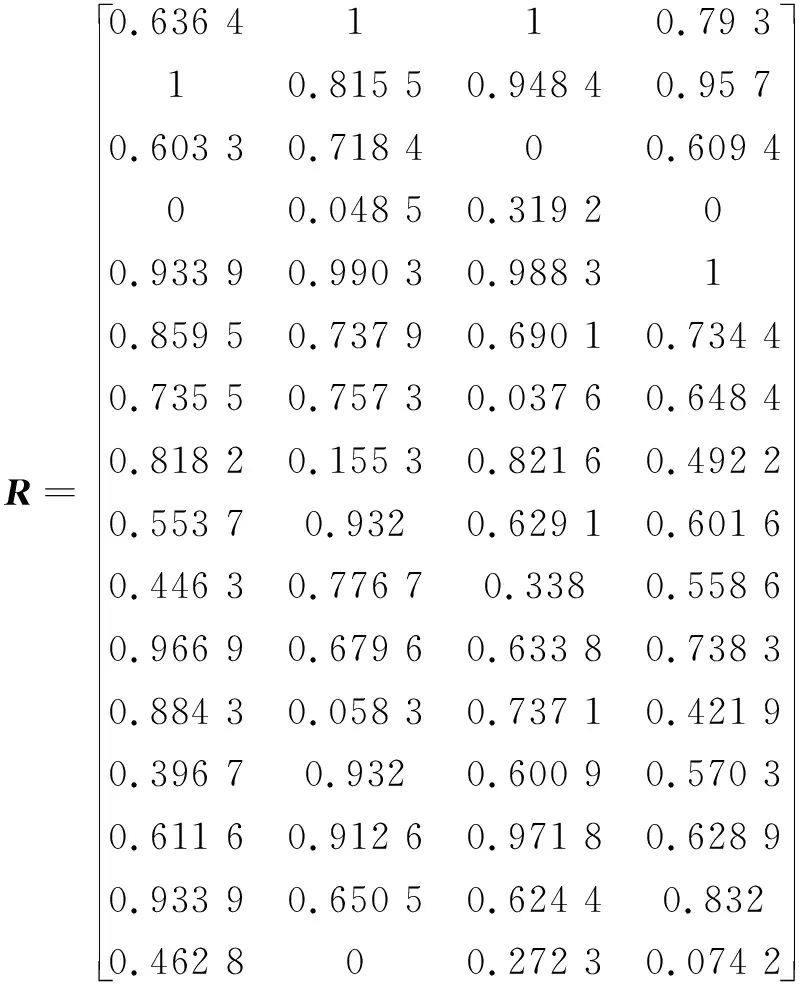
利用表4中的计算结果构建评价矩阵，再通过式(2)进行归一化处理，形成特征矩阵R：

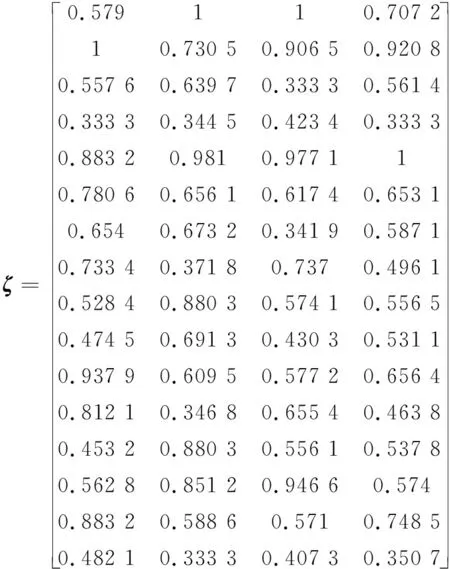
将矩阵R带入式(4)～(7)可计算出灰色关联系数矩阵ζ：

根据式(8)～(10)求得熵值法客观权重：

αj=[0.256 4 0.249 4 0.239 5 0.254 7]

主观权重：

βj=[0.213 0.226 0184 0.377]

按(11)式计算组合权重：

ωj=[0.217 5 0.224 4 0.175 5 0.382 6]

经组合赋权后，各指标权重大小依次为：右侧拱顶沉降>围岩应力>地表沉降>初支剪应力。由式(12)计算目标函数的灰色关联度(见表5)，关联度越大，方案越好，隧道稳定性越高。由表5可知 ：工况5的关联度为0.966 3，说明正交试验中工况5的方案为最优方案，其次是工况2，关联度为0.892 8。工况16的关联度为0.385 3，是本次试验中关联度最低值的组合，故工况16是最差的方案，隧道稳定性也最差。

其中各水平的平均关联度如表6所示。施工工序2的平均关联度最高为0.753 3，说明隧道施工工序2是施工工序中的最优选项。其次“加固区厚度3 m和强度200 MPa”的平均关联度较高为0.777 6，说明该组合是加固方式和范围的最优选项。“Ⅰ，Ⅱ部导洞错开距离、加固区范围和强度”平均关联度的极差为0.348 2，故可知其对隧道稳定性影响最大；施工工序平均关联度的极差为0.223，可知其对隧道稳定性影响较大；施工步距平均关联度的极差为0.096 6，故可知对隧道稳定性影响最小。从表6可知，平均关联度越高，说明该项指标越好，故最优方案为：加固区厚度为3 m，强度为200 MPa，施工步距为2 m，Ⅰ，Ⅱ部导洞错开距离为10 m，施工工序2。最优方案恰好为表5中的工况5，其关联度为0.966 3。

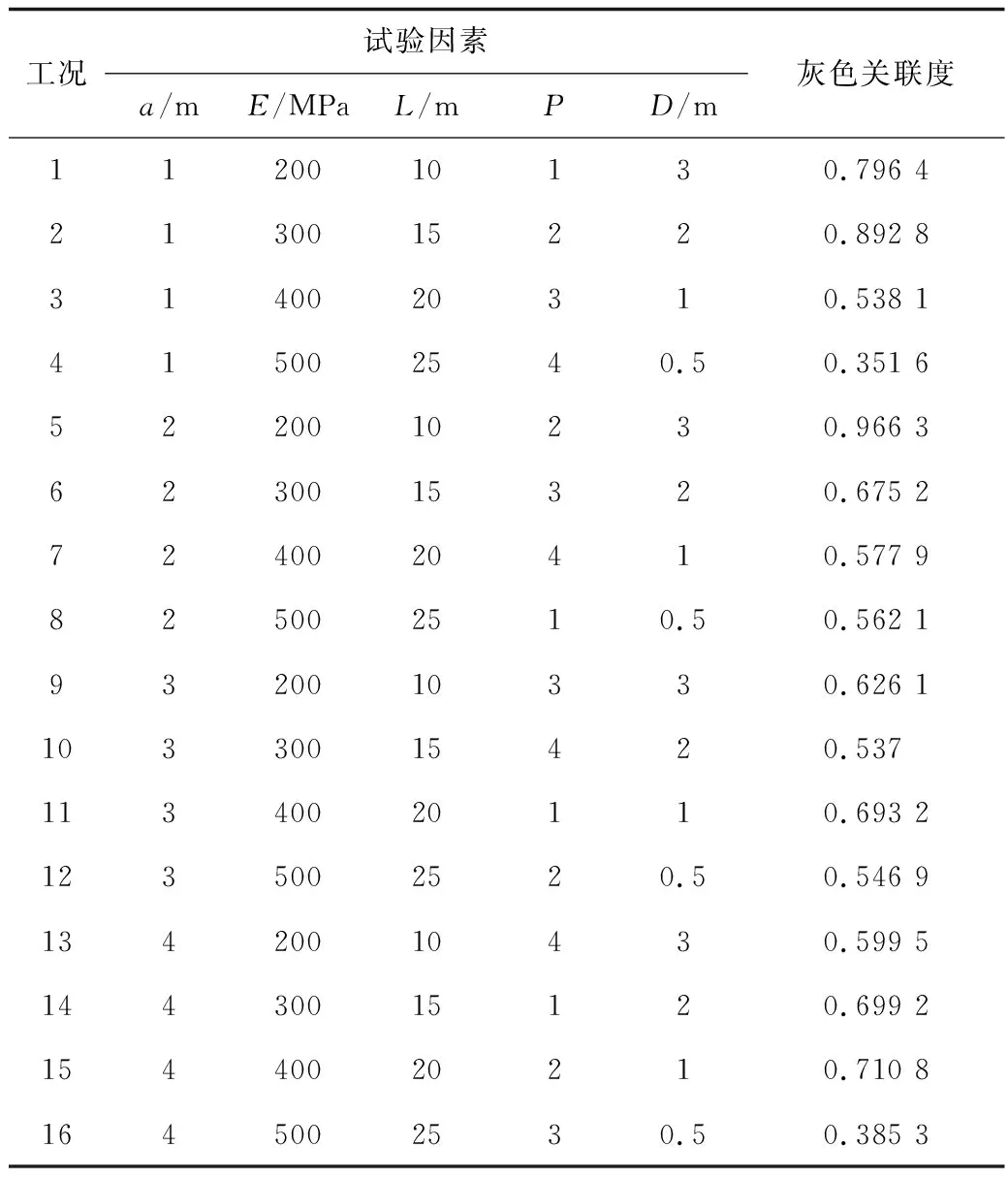
表5 目标函数的灰色关联度Table 5 Grey correlation degree of objective function

3 优化设计与结果分析

3.1 优化设计

将最优施工方案组合与原始设计组合“步距为2 m，加固区强度为500 MPa，Ⅰ,Ⅱ部导洞错开距离为15 m，施工工序1，加固区厚度为1 m。”优化前后有限元结果对比分析结果如表7所示。最优方案在各方面结果均比原始设计小，因此隧道整体受力得以显著改善，隧道稳定性更好。尤其最优方案的剪应力比原始方案小12.55 Mpa，确保喷混不会发生剪切破坏。地表沉降和右侧导洞拱顶沉降变形均小于30 mm，满足地铁施工规范要求。

表6 各水平平均关联度Table 6 Average correlation degree of each level

表7 优化前后有限元结果对比分析Table 7 Comparative analysis of finite element results before and after optimization

3.2 多种分析法的结果比较

为了进一步说明本文采用方法的准确性与先进性，另外采取2种方法对隧道的数据进行处理，由于篇幅原因，各方法不做具体说明。其中方法1采用传统灰色关联度法，计算权重为1/n；方法2采用熵值法—灰色关联度计算，方案3为本文方法。各方法的灰色关联度计算结果如图4所示。

图4 各种方法对比分析Fig.4 Comparative analysis of various methods

从图4可知：3种方法计算的关联度大小无明显差异，方法3最大灰色关联度为0.966 3，而方法1最大灰色关联度为0.960 3，方法2的灰色关联度为0.959 8，三者差距甚小，而且最优方案均为方案5，验证了本文方法的准确性。从图4中可知方法1和方法2几乎没有差别，因为熵值法计算各评价指标的权重大致相同，和方法1的权重系数1/n计算结果大致相同。但是方法1传统灰色关联度默认所有指标权重相同，导致精确度不高，只能粗略的得出最优方案，当各方案差距较小时，会出现灰色关联度相同的方案，难以抉择，方法2与方法1类似。

本文方法将熵值法和层次分析法进行结合，形成组合赋权，将定性分析和定量分析有效结合计算权重，且通过图4验证其准确性。本文方法在评价指标类型和数据较多时更为适用，特别是在各方案差距较小时，很少出现灰色关联度相同的方案，更容易凸显最优方案，这也是本方法的先进性。

3.3 施工沉降分析

北京地铁17号线天通苑站采用本文最优方案5施工，固定分区Ⅰ部平均每天掘进1 m，待固定分区Ⅰ部掘进10 m后，开始施工动态分区Ⅱ部，动态分区Ⅱ部每天掘进1.5 m。

施工地表沉降监测数据如图5所示。施工监测最大地表沉降为-23.2 mm，比模拟结果大10.8%，因为施工现场经常出现钢拱架支撑不及时；钢拱架未快速封闭成环等因素，造成施工结果偏大。

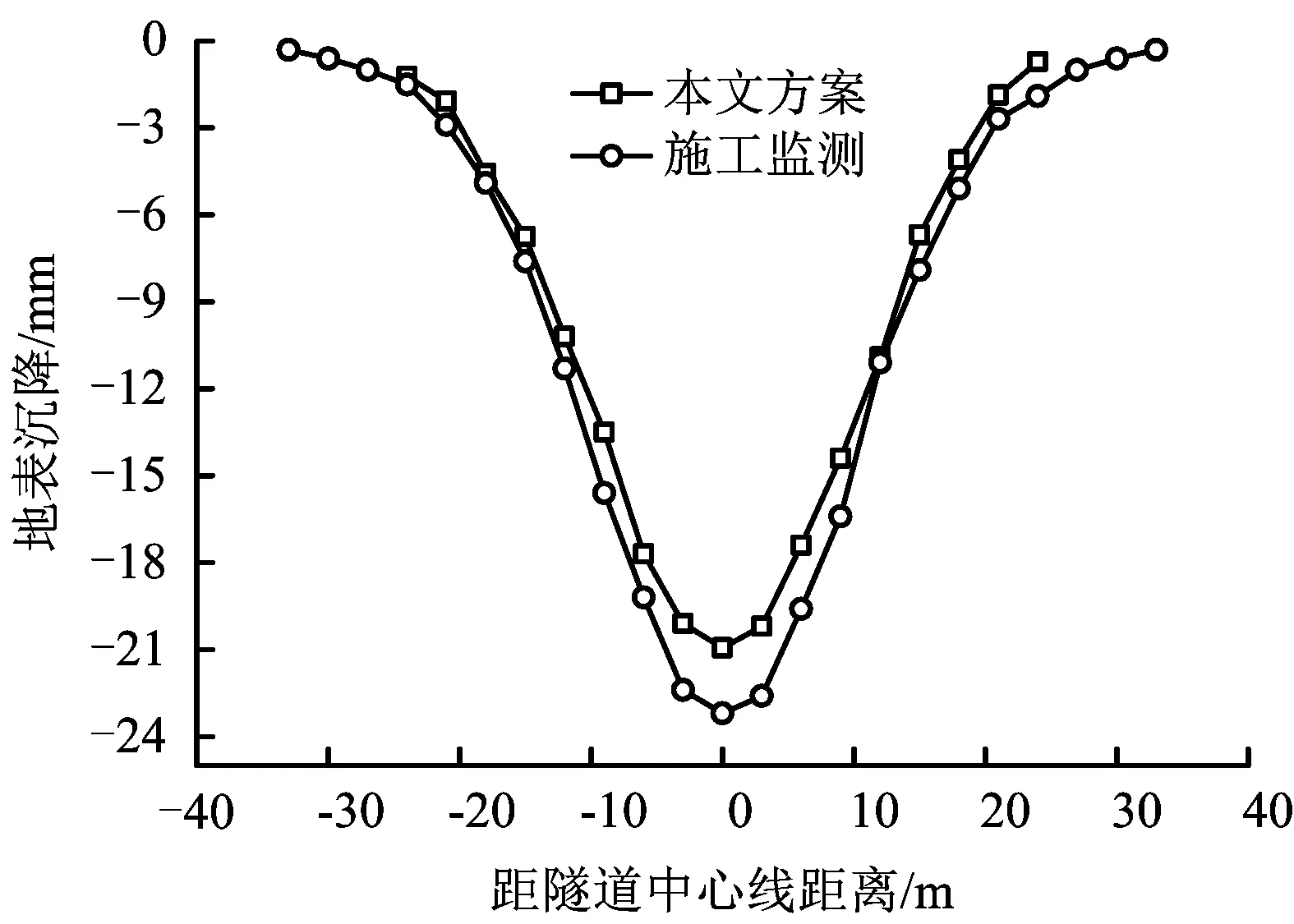
图5 数值模拟和施工监测地表沉降对比Fig.5 Comparison of ground settlement of numerical simulation and construction monitoring

4 结论

1)采用的正交试验、组合赋权-灰色关联度方法研究浅埋暗挖大断面隧道稳定性的影响因素，从平均关联度可知：隧道施工工序、加固区强度和范围、Ⅰ，Ⅱ部导洞错开距离对隧道整体稳定性的影响较大，施工步距对隧道整体稳定性的影响较小。

2)本文方法选择出最优施工方案的各项数据均优于原始方案；且与其他2种方法对比分析验证了本方法的准确性，特别在样本数量和差距均较小时，更能凸显各样本的优劣。

3)组合权重通过熵值法对数据进行客观处理，更加真实可靠，再通过层次分析法对数据进行主观评判，增强其逻辑性，最后得出的权重更加真实可靠。因此本文方法选择隧道施工方案是更加合理的。

4)在复杂环境条件下，合理选择施工方案，不仅能增强隧道稳定性，保证隧道顺利施工，而且能节约成本和时间，为项目带来巨大的经济效益和社会效益。本文方法能在短时间内准确的选出最优施工方案，并通过实际工程验证本方法的先进性，故本方法也能为其他复杂工程方案比选提供借鉴意义。