松散破碎岩石中气体渗流影响因素实验研究*

马 恒，王晓琪，齐消寒，艾纯明

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 阜新，123000； 2.辽宁省煤矿安全重点实验室，辽宁 阜新，123000)

0 引言

研究松散破碎煤岩的渗流性对防治瓦斯以及煤的自燃具有重要的实际意义。国内外学者对空气在多孔介质渗流已经有了丰富的研究。Darcy于1856年在实验的基础上提出了Darcy定律[1]。我国周世宁院士创造性地将描述多孔介质线性渗流特征的Darcy定律引入到煤层瓦斯流动中[2]。由于达西定律多适用于多孔介质中的低速粘性流，当流速高于某一临界值时，Darcy定律不再满足，呈现出non-Darcy现象。

煤是特殊的多孔介质，其复杂的孔裂隙系统使得瓦斯在煤体内的渗流往往遵循某种非Darcy渗流规律[3-4]。基于Fick扩散定律，周市伟等[5]根据煤体的异样结构、变质程度、大小不同粒径，探索了煤粒瓦斯扩散的影响程度；宋金星[6]通过实验室煤样地质强度因子的观测、启动压力梯度和渗透率测试方法，初步建立了启动压力梯度法和地质强度因子法用于判识瓦斯运移产出流态。

张志刚[7]采用实验研究的方法，阐述了吸附作用对煤岩非线性渗流特性的影响机制；李志强等[8]研究了温度对瓦斯在煤粒中扩散的影响；郭红玉等[9]运用测试启动压力梯度装置，证明了煤层气运移流态为非线性渗流；张先敏等[10]通过建立低渗透煤层气流动数学模型，探索了低渗透煤体中气体非线性流动的规律。

陈长华，郭嗣琮等[11-12]对非均匀孔隙介质中气体稳定渗流进行了研究,此项研究为煤自燃提供了分析手段；聂百胜等[13]依据气体在多孔介质中的扩散模式，分析了瓦斯气体在煤孔隙中的扩散机理。胡国忠等[14-17]对低渗透煤的瓦斯渗流规律进行了深入的研究。

现如今，多孔介质渗流理论研究大多采用建立模型，运用实验获得数据进行拟合，从而得到非达西渗流运动方程。其产生机理各个学者都有不同的意见，对于非线性渗流的模型学者们还是较多青睐于幂定律。因此对于非线性的达西定律基础上的瓦斯流动理论的深入研究是当下探索的重点方向。

经过查阅相关文献发现，在这些实验研究中对松散破碎岩石研究较少，在研究松散破碎岩石渗流规律过程中，设计的相关实验并没有同时考虑岩石的粒径大小、岩粒空间分布以及空气在介质中的渗流速度对气体渗流的影响。本文通过设计松散破碎岩石的气体渗流实验，进一步研究了破碎岩体渗透率的变化规律，而且也丰富了破碎岩石中气体渗流的实验方法。

1 渗流数学模型

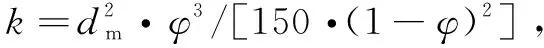
(1)

式中：v为渗流速度；k为渗透率，m2；ψ为运动粘性系数，风流取14.810-6；dm为颗粒的平均调和粒径，m；φ为孔隙率。

空气在多孔介质中流动，其雷诺数与孔隙率、渗流速度呈正相关关系。判定多孔介质渗流流体的速度表达式可表示为：

(2)

将研究多孔介质视为定常、不可压缩、无源渗流流动，且为等温过程，将非线性渗流公式在直角坐标系中展开，即可得到其气体质量守恒定律表达式：

(3)

式中：p为渗流压力，m2；β为颗粒形状系数，取值为1.5；g为重力加速度，9.81 m·s-2。

在考虑粘性损失和惯性损失后，采空区渗流的动量守恒定律可表示为：

(4)

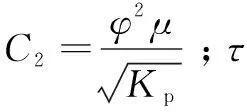
2 实验装置及材料

实验渗流测试系统如图1所示。该系统由供气装置、渗流装置、流量测量装置及压力测试装置组成。主体渗流装置主要是测试长度L=1 000 mm，半径R=95 mm的透明圆管，如图2所示。考虑到两端由于进风时风流不稳定影响所测的压力数据，所以在测试管的两端分别加上L=300 mm，R=95 mm的过渡段，使得测试的数据更加稳定、准确。在测试装置中添加所需测量的多孔介质，填充的两端使用填充介质粒径相适应的筛孔网固定。将两端的气流稳定管体(过渡段)与测试端用法兰紧密连接。供气装置为12.5 L/8 MPa微型真空泵。空气通过连接装置器流入到测试管中。此时，在两端的过渡段放置皮托管，目的是通过连接微压计来测试空气通过多孔介质的压差。在测试系统的端部设计一个浮子流量计，目的是用于测定管内通过的流量。微压计最大量程为4 000 Pa。浮子流量计的最大量程2.5 m3/h。相似模拟实验材料包括12种不同粒径(d=4，5，6，7，8，10，12，16，20，25，28，35 mm)的玻璃球体，如图3所示。包括5种不同粒径(d=6，8，10，12，25 mm)的碎石子(碎石子的粒径是通过筛网确定的)，如图4所示。

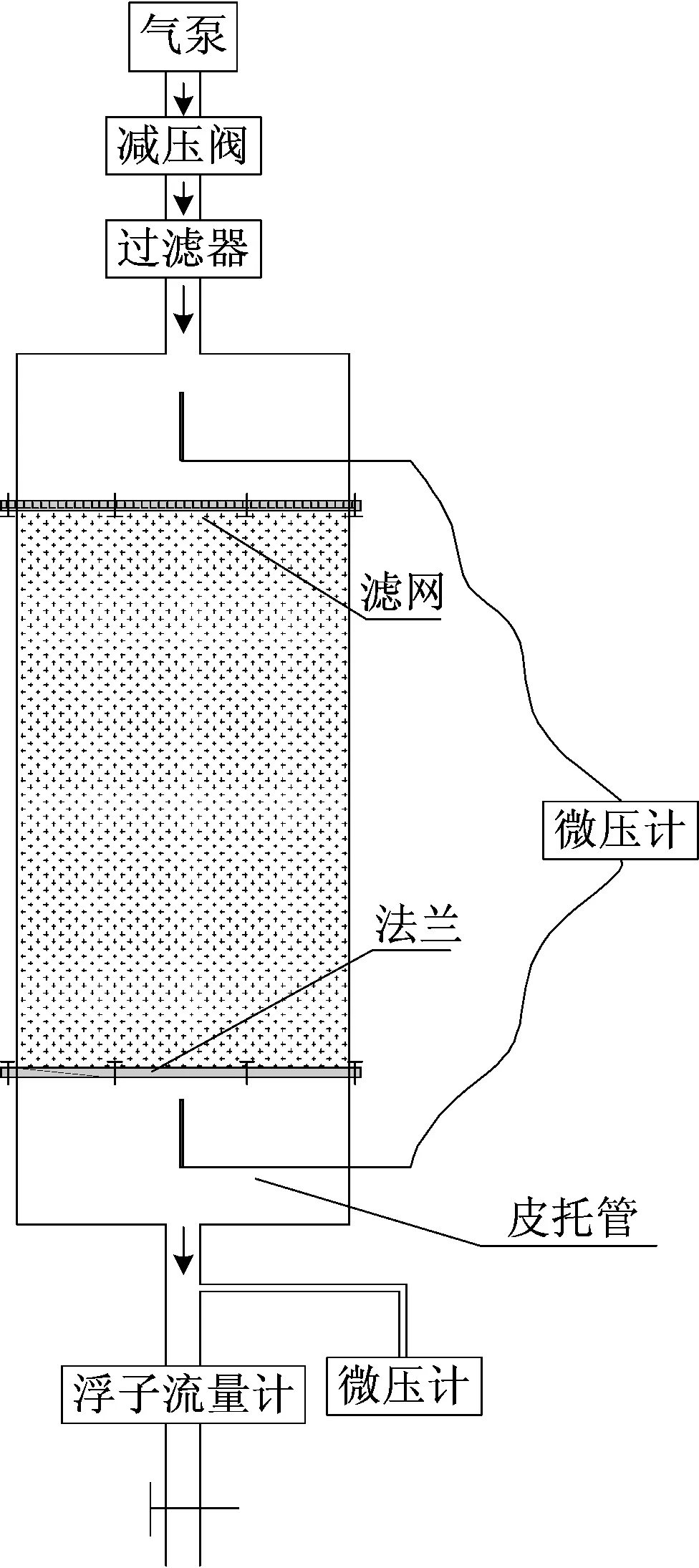
图1 相似模拟实验渗流测试系统Fig.1 Seepage test system with similar simulation experiment

图2 多孔介质填充段Fig.2 Filling section with porous media

3 实验过程

为了使实验更具有目的性，使测得数据更科学，更准确，对实验条件进行如下简化。假设渗流相似实验符合以下条件：

1)空气为不可压缩流体。

2)破碎的煤或岩体自身无气体释放。

3)不考虑介质所受的力。

4)渗流过程为等温过程。

实验装置如图2所示。依据实验填充多孔介质粒径的不同，在测试系统管的两端安装符合要求的滤网；在填充的时候，使用震动实验装置使其能够紧密填充；根据填充前后的质量，求出填充多孔介质的质量。固定好渗流装置的两端，保证其良好的气密性；将装有填充介质的渗流装置连接到其他部件，打开微型真空泵，通过手动调节按钮控制不同的流量，在压差计示数达到稳定状态后，读取读数即可；记录完每组实验流量以及压差计读数后更换不同粒径的介质重复上述的实验步骤。

图3 不同粒径的测试玻璃球(从左到右粒径大小分别为35，28，25，20，16，12，10，8，7，6，5，4 mm)Fig.3 Tested glass spheres with different particle sizes (Particle size from left to right was 35,28,25,20,16,12,10,8,7,6,5 and 4 mm respectively)

图4 不同粒径的测试碎石子(从左到右粒径大小分别为6，8，10，12，25 mm)Fig.4 Tested gravel with different particle sizes(Particle size from left to right was 6，8，10，12，25 mm respectively)

在进行采空区渗流实验过程中，先对12种单一的粒径玻璃球构成的堆积介质进行均质各向同性的实验研究；然后对单一粒径的碎石子进行非均质的实验研究。在单一粒径构成多孔介质的实验基础上，再将6，12，25 mm粒径的玻璃球按照不同体积比进行混合，将相似粒径的碎石子6，12，25 mm按照不同比例进行混合；最终分析单一粒径球体(均质)、石子(非均质)、混合粒径玻璃球体、混合粒径碎石子渗流规律，以及不同介质、填充的粒径大小、填充多孔介质孔隙率对气体渗流的影响。

3.1 粒径和孔隙率的关系分析

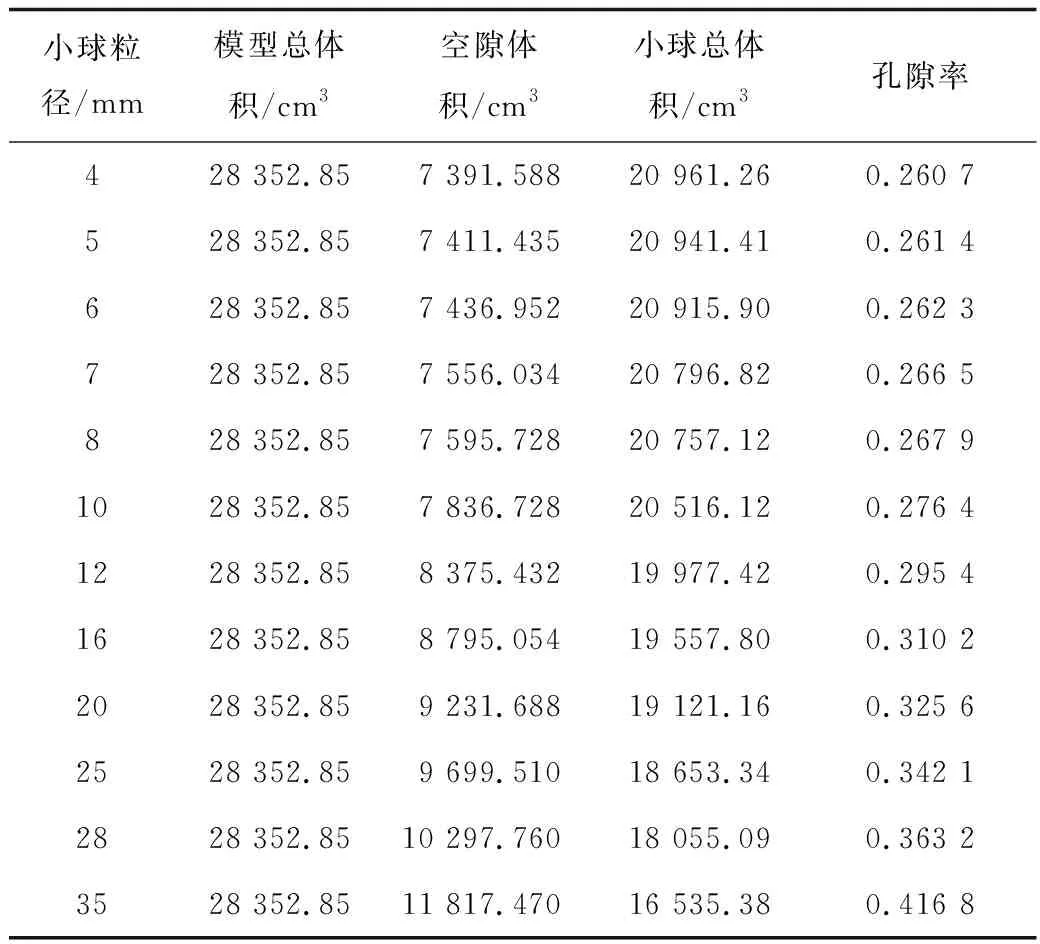
实验中将12种单一粒径的玻璃球体依次填充在渗流测试的实验装置内，使其紧密填充。称量分别得到平均质量M、每组填充前的质量以及填充完的总质量，算出每组粒径玻璃球体的填充质量并进行记录。再分别测量出每一种单一粒径的球体质量m，因为玻璃球体的体积可知，可以求出每种粒径填充的玻璃球体所占的总体积V球。因为渗流实验装置模型的总体积V可知，所以可以算出孔隙的体积V孔，求出每种粒径填充时的孔隙率P，如式1。测量数据见表1。

(5)

基于表1数据，绘制了不同粒径—孔隙率之间的关系图，如图5所示。

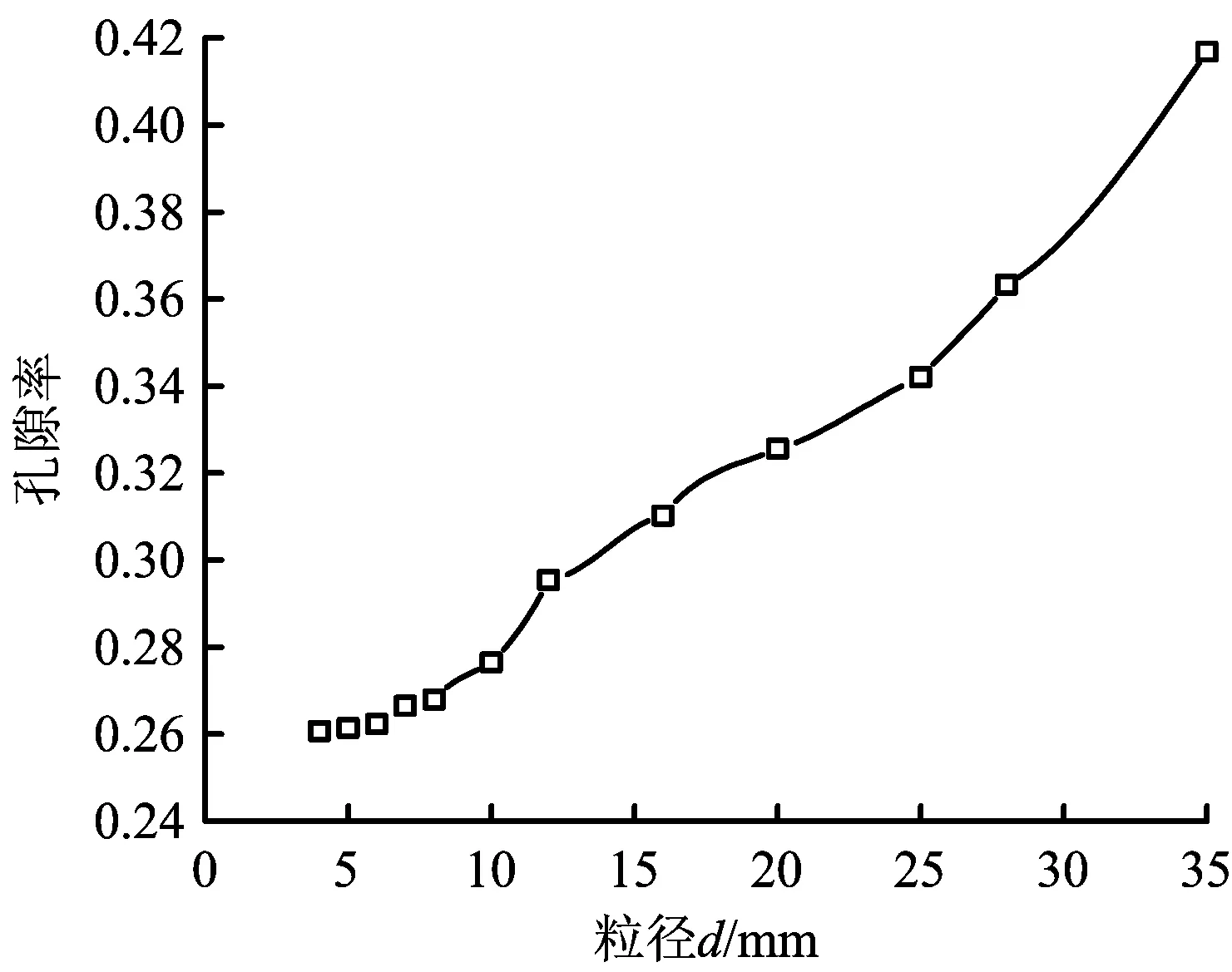
图5 不同粒径小球和孔隙率关系Fig.5 Relationship between different particle sizes and porosities

根据粒径和孔隙率的散点图通过拟合，得到拟合公式为y=0.004 8x+0.233 3；其中各种测试粒径玻璃球体的粒径大小与孔隙率的相关系数在0.98以上，说明两者具有很好的相关性。从图5可以看出，粒径与孔隙率呈正相关关系。

3.2 粒径、渗透速度对渗透压力的影响

测试由12种粒径不同的玻璃球体单独构成的自由堆积多孔介质，其流量与压力梯度数值。流量的测试范围从0.1～1 m3/h，测试出了10组数据。实验测得流量将其转换成比流量(渗流速度)，测得的压力差值转换成压力梯度。将12种单一粒径的玻璃球体渗流速度和对应的压力梯度绘制成散点图，如图6所示。

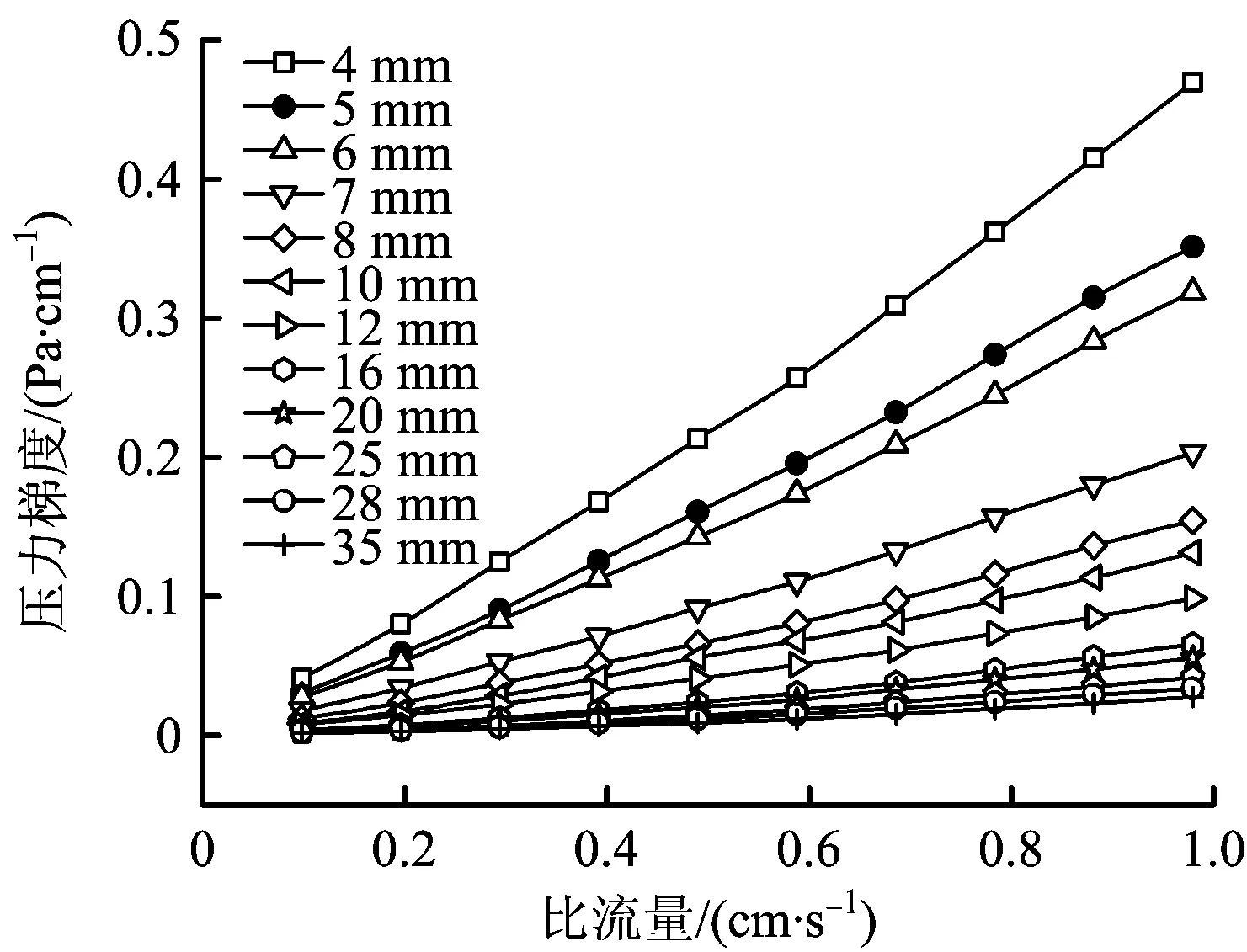
图6 单一粒径的玻璃球体渗流速度与对应的压力梯度散点图Fig.6 Scatter plot graph of seepage velocity of glass sphere with single particle size and corresponding pressure gradient

根据图6分析得到，12种单一粒径的玻璃球体作为堆积介质构成的多孔介质空间，渗流速度与压力梯度呈现正相关关系。其中粒径为d=4，5，6，7，8，10，12 mm的小玻璃球体的渗流速度与压力梯度的变化趋势基本为线性，渗流符合Darcy定律。根据达西定律，拟合直线的斜率可表示实验填充多孔介质的渗透率，对于同一种流体而言介质的渗透率应该为定值。

当粒径为d=16，20，25，28，35 mm时，渗流状态渗流速度开始出现明显的非线性渗流，由实验可以得出，渗流的起始阶段都比较符合线性渗流定律。随着粒径的逐渐增大，渗流状态由线性渗流转变为非线性渗流状态，其渗流速度的值也在不断地减小。很明显，空气在大粒径组成的多孔介质中的渗流系数不是一个常数。

3.3.2推进农村生活垃圾治理 指导长江经济带11个省(市)按照“标本兼治、综合施策、突出重点、分类施策”要求，做好非正规垃圾堆放点排查和整治工作。建立农村生活垃圾集运处置体系，鼓励具备条件的地方实行村收集、镇转运、县处理。有条件的地区要推行适合农村特点的垃圾就地分类和资源化利用方式。发挥好村级组织作用，增强村集体组织动员能力，支持社会化服务组织提供垃圾收集转运等服务。

4 非均质各向同性多孔介质渗流实验

上述实验分析是以单一粒径的玻璃球作为填充物，其多孔介质是均质各向同性的，但实际松散破碎岩石是非均质各向异性的。为使相似模拟实验更加准确，故采取更加贴近实际的碎石子作为填充物进行实验分析，形成非均质实验条件。

4.1 粒径和渗透速度对渗透压力影响分析

对5种粒径(粒径为d=6，8，10，12，25 mm)的碎石子，单独构成的自由堆积体非均质各向多孔介质进行渗流测试实验。

流量的测试范围0.1～1 m3/h。测试出了10组数据。根据实验得到了在不同流量下的压差变化值。基于得到的数据值，将不同渗流速度与相对应的压力梯度绘制成散点数据图，如图7所示。

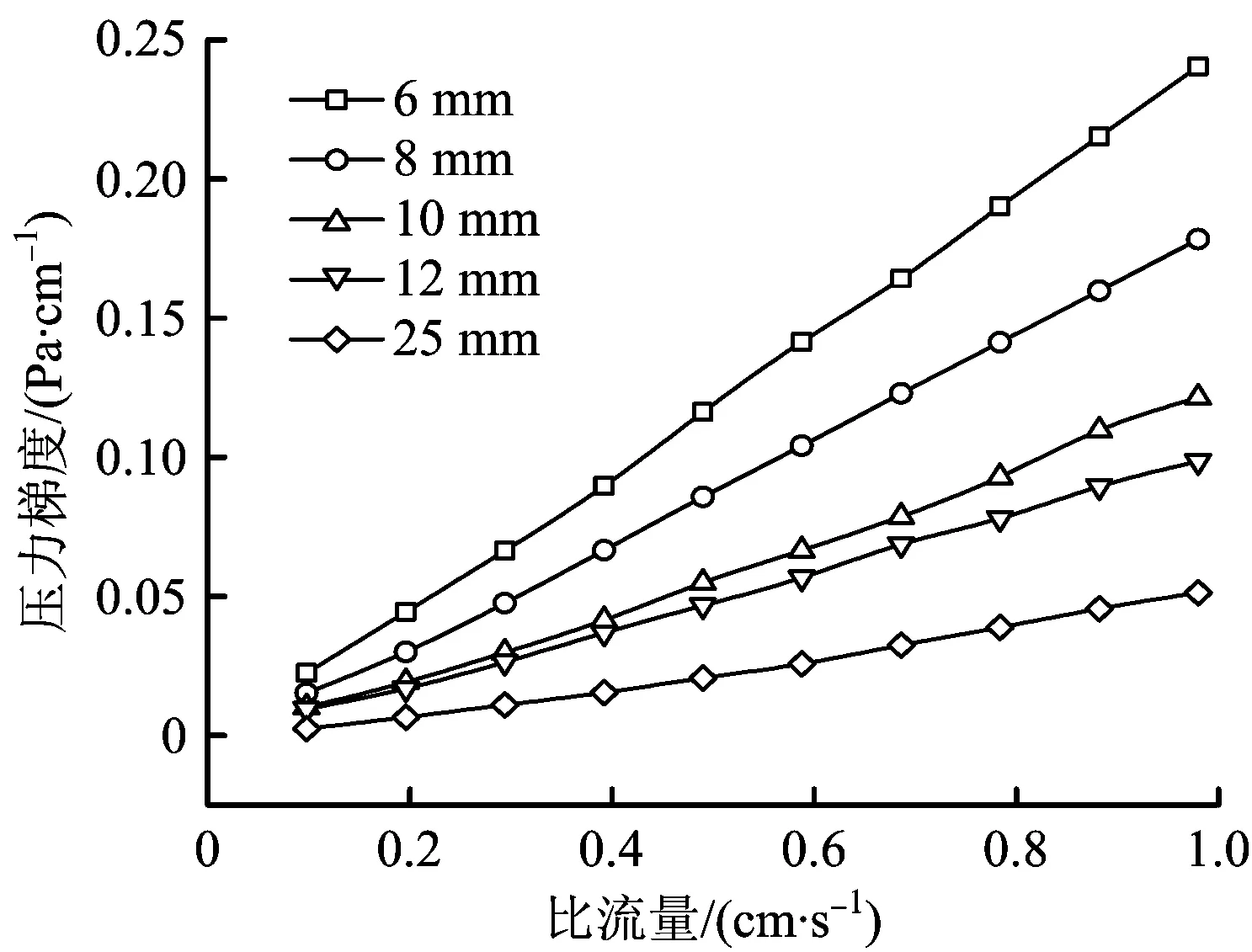
图7 不同粒径的碎石子渗流速度与压力梯度Fig.7 Seepage velocity and pressure gradient of gravel with different particle sizes

从图7中可以看出，以单一粒径的碎石子作为堆积介质构成多孔介质空间，随着渗流速度的增加压力梯度也在不断地增加。渗流刚刚进行的时候，渗流的规律符合Darcy定律。随着空气渗流速度的增大，其渗流状态由线性向非线性渗流转变。测试结果表示：随着填充介质粒径的逐渐加大，渗流状态也由线性向非线性渗流转变。

通过前面对玻璃球体进行实验得到的渗流速度和压力梯度的数据和拟合曲线，与碎石子的数据作比较。分析研究相同粒径的玻璃球体和碎石子，不同渗流速度下对应的压力梯度，如图8所示。

由图8可以看出，相同粒径下，在粒径较小时的碎石子和小球变化规律不一致，因为碎石子的形状不规则，填充受到多种因素的影响。但粒径较大时不论均质还是非均质其变化规律基本一致。

图8 相同粒径下的碎石子和小球渗流速度与压力梯度Fig.8 Seepage velocity and pressure gradient of gravel and ball with same particle size

5 原煤仓纵深方向多孔介质渗流实验

5.1 不同粒径球体填充渗流实验

图9 混合小球充填示意Fig.9 Schematic diagram of mixed ball filling

图10 混合碎石子充填示意Fig.10 Schematic diagram of mixed gravel filling

由图11看出，均质小球随着速度的增加，渗透的压力梯度都在逐渐增高。其中图11(a)压力梯度随着渗透速度变化更为明显，即由于小粒径玻璃球体所占比例发生变化，引起压力梯度变化更为明显，小粒径所占比例越高，压力梯度变化越大。图11(b)压力梯度随渗透速度变化较小，虽然大粒径占值比例越来越大，但是压力梯度增加并不明显，特别是大粒径占40%和50%的2条曲线近乎重合，几乎没有变化。图11(a)和图12(a)渗透速度与压力梯度均呈现非线性变化规律，说明在测试方向上，当孔隙率发生变化时，无论粒径多大，渗流都不再符合线性规律，而是呈现非线性规律。

表2 10组实验6,12,25 mm时各占的体积比Table 2 Volume ratio of ten group of 6,12 and 25 mm respectively %

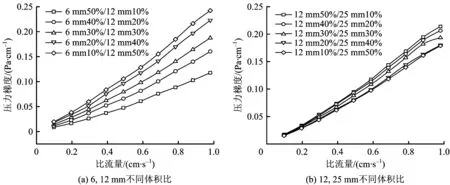
图11 “均质”小球渗流速度与压力梯度Fig.11 Seepage velocity and pressure gradient of “homogeneous” ball

图12 “非均质”碎石子渗流速度与压力梯度Fig.12 Seepage velocity and pressure gradient of “heterogeneous” gravel

从图11与图12进行对比可以看出，不同比例玻璃球体和碎石子填充构成的多孔介质渗流的规律基本相同。

6 结论

1)粒径大小和渗透速度与渗透压力梯度呈现正相关关系；在保证相同的渗流速度情况下，孔隙率是影响压力梯度变化速率的主要因素。

2)随着粒径增大，渗流状态由线性渗流转变为非线性渗流的渗流速度的值在不断减小。

3)小粒径所占比例发生变化，引起压力梯度变化更加明显，小粒径所占比例越高，压力梯度变化越大。

4)渗透速度与压力梯度均呈现非线性变化规律，说明在测试方向上，当孔隙率发生变化时，无论粒径多大，渗流都不再符合线性规律，而是呈现非线性规律。