基于集成学习的阶跃型滑坡阶跃点判别分析
2019-09-06杨光辉简文星张树坡付智勇
杨光辉,简文星,张树坡,付智勇
(中国地质大学(武汉)工程学院,湖北 武汉 430074)
0 引言
三峡库区地质灾害众多,其中滑坡是三峡库区内最为常见的地质灾害。据不完全统计,库区内滑坡分布多达4 200多处[1],这些滑坡严重威胁到社会经济发展和群众生命财产安全。
三峡库区滑坡的稳定性受季节性降雨和库水位涨落影响,其中一类滑坡的位移监测曲线在降雨、库水位等外界作用下近似为台阶型,即累积位移—时间曲线在极端降雨或者大幅水位波动作用下变形显著增加,随着外界影响因素的作用减弱,逐渐平稳,整个变形曲线表现为台阶状,此类滑坡被称为阶跃型滑坡。针对阶跃型滑坡累积位移—时间曲线这一台阶状特征,基于诱发因素的滑坡—位移预测模型被提出[2]。该模型将滑坡位移分解为趋势项和波动项,认为波动项是由降雨和库水位等环境因素所引发[3-4]。随着机器学习理论的兴起,BP神经网络[5]、支持向量机(SVM)[6]、极限学习机(ELM)[7]等非线性模型被广泛用于滑坡位移预测。为了进一步提高机器学习模型的预测精度,越来越多学者开展群优化算法的机器学习模型研究[8-9]。缪海波等[10]采用非平稳时间序列、Pearl曲线和BP人工神经网络这三种模型预测八字门滑坡位移。向玲等[11]将BP神经网络运用于白家包滑坡位移预测,预测趋势与位移真实值趋势基本一致。邓冬梅等[12]提出了基于时间序列集合经验模态分解(EEMD)和粒子群优化的支持向量机回归(PSO-SVR)位移预测方法,并对三峡库区内几个阶跃型滑坡位移进行了预测,预测结果与实测位移较吻合。周超等[13]提出了一种基于诱发因素响应分析的进化支持向量机位移预测模型,并以三峡库区典型的阶跃式滑坡—八字门滑坡为例进行位移的预测模型,取得了较好的预测效果。彭令等[14]基于时间序列分析与进化支持向量机的滑坡位移预测模型,研究了阶跃型滑坡位移变化规律与季节性影响因素之间的响应关系,结果表明此模型是一种行之有效的滑坡位移预测方法。以上研究均侧重阶跃型滑坡的位移预测,而关于阶跃型滑坡的阶跃点的研究较少。阶跃点是滑坡位移大幅增加的点,此时滑坡可能失稳并造成一定的经济损失。故本文针对阶跃型滑坡阶跃点判别进行研究。
1 理论方法
1.1 聚类分析
聚类分析是将数据集中的样本尽可能划分为彼此并不相交的子集,每个子集被称之为“簇”。通过聚类分析,可以通过无标记训练样本的来揭示数据内在的性质及规律,为后续数据分析提供基础。目前常用聚类分析算法主要包括K均值算法、两步聚类算法、密度聚类算法和高斯混合聚类等聚类算法[15]。两步聚类分析既可以处理连续数据又可以处理离散型数据,并且可以根据一定的准则自动确定聚类数目,因此被广泛利用[16]。
2001年CHIU等[17]对传统BIRCH算法进行改进,提出了一种能处理大规模数据的两步聚类分析算法。该方法主要通过预聚类和聚类两个子步骤实现对数据的聚类。首先通过“序贯”方式对样本进行粗略划分,然后依据数据“亲疏程度”判定选中的样本是否纳入新的子类,或者创建另一个子类。与传统聚类算法相比,两步聚类算法采用距离测度样本之间的亲疏程度。针对数值型变量,采用欧式距离对其进行判别;当样本中含有离散型变量时,采用对数似然法进行衡量。最后反复执行此步骤,将数据分为N个类别。随着聚类的进行,聚类数目逐渐减少,最后完成整个数据的分类。
1.2 集成学习
集成学习是通过构建并且结合多个学习机来完成分类或者回归任务的一类机器学习方法。其中,基于自助采样法(bootstrap sampling)的Bagging算法是并行式集成学习的代表。假定包含n个样本的数据集K,每次从K中都抽取一个样本,将其复制到数据集K’,然后放回原数据集K中。重复n次抽取,则每个样本不被抽到的概率可用式(1)计算:
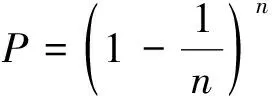
(1)
对式(1)取极限,得到每个样本不被抽到的概率,如式(2):
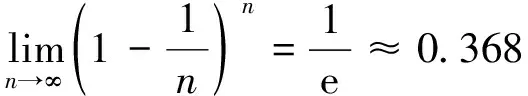
(2)
式(2)表明,约有36.8%的样本没有出现在数据集K’中。因此,可以利用数据集K’对模型进行训练,然后利用没有出现在数据集K’中的数据(包外数据)对模型进行测试,检验模型的准确性。依据上述流程,假定共有n个样本,每次在数据集D中采出m个样本组成s个训练集和测试集,然后利用训练集数据训练得到s个问题模型,最后利用问题模型对测试集进行预测并将预测结果进行结合,这就是Bagging算法的基本流程。Bagging算法利用投票法解决分类问题,而利用简单平均法解决回归问题。
随机森林(Random Forest)是以决策树为基学习器的一种Bagging算法的扩展变体。不同于传统的决策树算法,随机森林引入了随机属性选择。传统的决策树在当前节点进行属性划分时,在属性集合(假设有m个属性)中选择一个最优的属性进行划分。而随机森林中每颗树的节点,先从属性集合中随机选择一个包含k个属性的集合,然后再从k个属性集合中选择最优的属性进行划分。随机森林通过多个属性扰动的方式提高了个体学习器的泛化性能。随机森林计算量小、鲁棒性高、对数据集数量和质量要求不高,并且在具体实际应用过程中展现出了强大预测能力。本文运用聚类分析和集成学习的方法建立了阶跃型滑坡识别和判别模型(图1)。

图1 模型流程图Fig.1 Flow chart of the model
2 案例分析
2.1 八字门滑坡

图2 八字门滑坡平面图[18]Fig.2 Plan of Bazimen Landslide
八字门滑坡处于三峡库区秭归县境内,香溪河右岸。八字门滑坡为切层堆积层滑坡,地势呈阶梯状,西高东低,前后缘高差约150 m,东西长约550 m,滑坡地面平均坡度40°~60°。滑坡主滑方向约SE110°,平均滑体厚度约30 m,总体积约4×106m3(图2)[18]。滑体主要为松散的崩坡积、残坡积物,滑体自上而下可分为填筑土、粉质黏土夹碎石层、碎石土层,滑坡主要存在两层滑带:主滑带和次级滑带(图3)[19]。
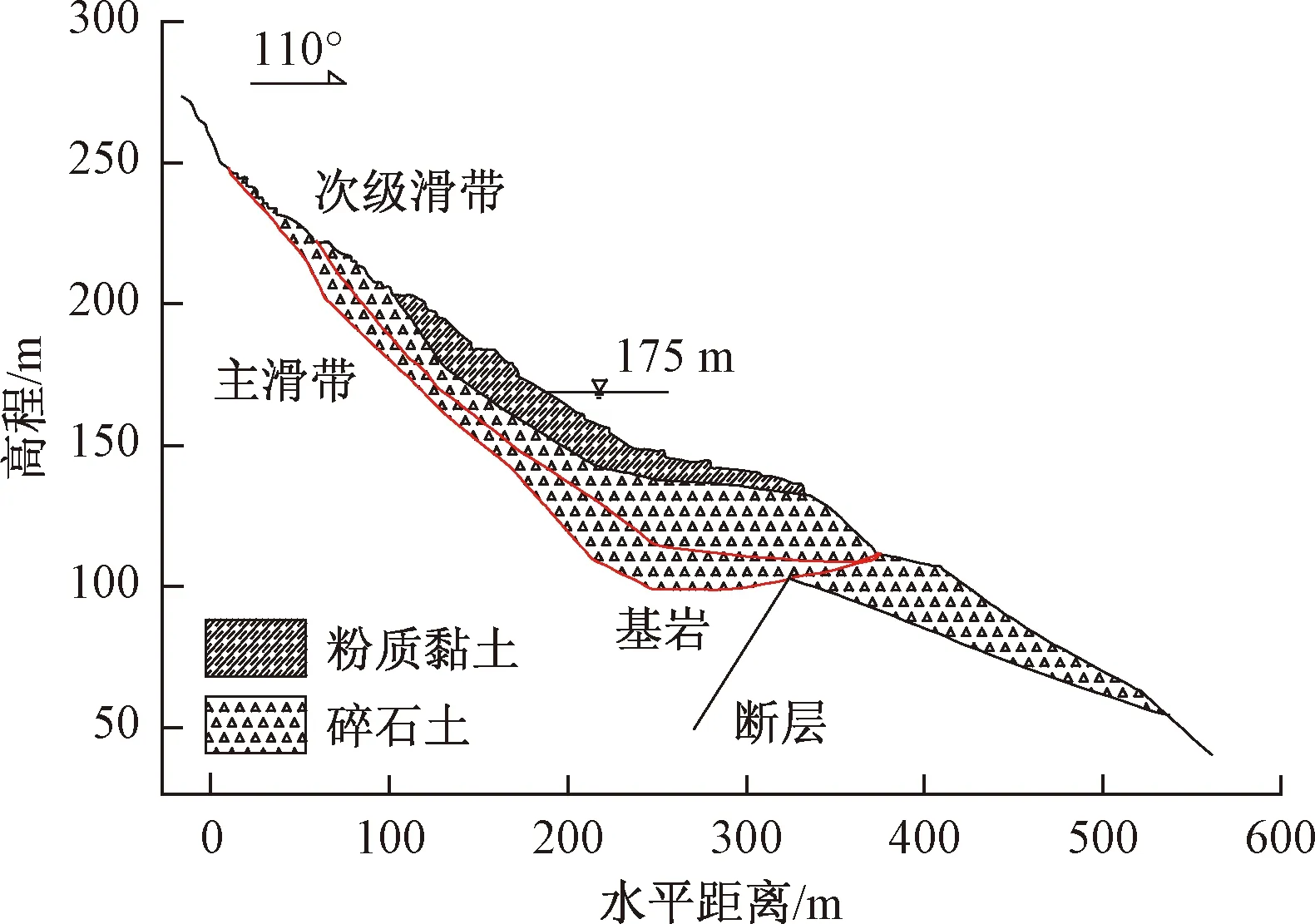
图3 八字门滑坡工程地质剖面图[19]Fig.3 Geological profile of Bazimen Landslide
自三峡库区2003年蓄水开始,滑坡体就出现了明显的变形。由于滑坡前缘在库水位以下,库水位的变化对滑坡体的稳定性影响较显著,在库水位变化和降雨等因素影响下滑坡位移速率有增大的趋势。三峡库水位2009年9月首次达到175 m,故本文选取2010年4月至2016年12月共80个滑坡位移和相应的库水位、降雨监测数据进行分析(图4)。
2.2 位移速率的聚类分析
阶跃型滑坡不同于其他滑坡,其位移曲线表现出明显的台阶型特征。即在水库正常运行时期,滑坡位移增加缓慢或者几乎不增加;在库水位急剧下降和极端降雨时期,滑坡位移急剧增加。因此,在滑坡位移速率曲线中出现明显异常点。聚类分析依据数据内部本身属性对数据进行分类,因此可以采用聚类分析对八字门滑坡位移速率进行分类。本文采用SPSS软件对位移速率进行两步聚类分析(表1)。由表1所示,滑坡处于稳定性变形阶段被划分为第3类,共有63个点;滑坡处于急剧变形阶段,被划分为第1类,共有15个点。其中2010年7月滑坡位移速率超过研究阶段所有位移速率,两步聚类算法中将其划分为第2类,显然该点为阶跃点,为此合并第1类和第2类见表2。

图4 八字门滑坡降雨、库水位及位移监测数据Fig.4 Monitoring data of rainfall, reservoir water level and displacement of Bazimen Landslide

类别单位位移增加速率/(mm·month-1)均值方差个数164.9726.45152204.99/13-0.6712.8563组合14.3937.6579
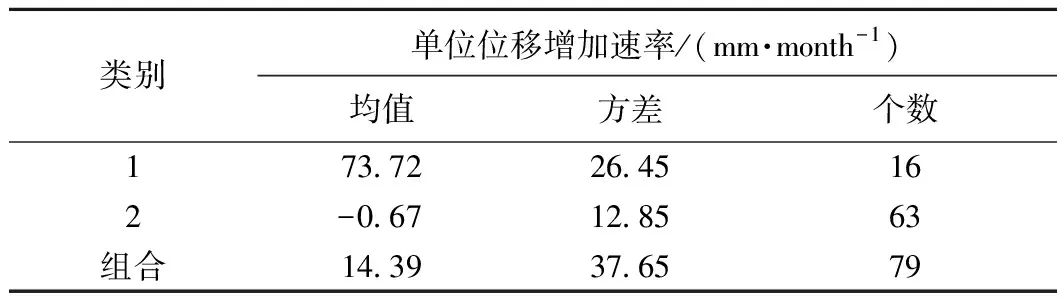
表2 合并后聚类分析结果

图5 人工筛选验证聚类分析结果Fig.5 Analysis results of verification and clustering by manual screening
为了叙述方便和更好地区分阶跃点,将同一个台阶内的阶跃点称之为组内阶跃点,两个台阶分界点的阶跃点称之为组外阶跃点。最后,通过人工筛选阶跃点验证聚类分析结果。如图5所示,滑坡所有的组外阶跃点(共8个)全部被识别为第1类,表明聚类分析算法具有较高的准确性。同时为了进一步证明两步聚类分析的准确性,采用K值聚类分析算法对滑坡位移增加速率再次进行聚类分析。结果表明,K值聚类分析与两步聚类分析约有99%的重合,表明两步聚类结果分析对阶跃点识别具有较好的辨识能力。但2015年9月点判别结果出现较大差异,K值聚类分析结果认为该点为第3类点,两步聚类认为该点为第1类点。究其原因,该点位移增加速率为31.92 mm/month,大致位于第1类和第3类数据均值点附近。按照聚类分析中“距离定义”,既可以认为该数据点第1类点又可以认为该数据为第2类点,使得算法对该点进行判别时出现混乱。该点位于滑坡稳定变形阶段,但该点前后位移增加速率几乎为0。因此,作者认为该点为滑坡位移阶跃点。
2.3 多场信息变形判别
众多研究表明,滑坡位移受降雨和库水位波动控制。降雨量较大的月份,滑坡位移增加速率增大,降雨量较小的月份,滑坡位移增加速率减小,位移几乎保持不变。例如,在2013年7月,滑坡区域普遍下起暴雨,月降雨量达到206.1 mm,直接导致滑坡单月位移速率由-0.07 mm/month增加到83.17 mm/month。随着降雨量降低,滑坡波动项位移逐步降低,总位移几乎保持不变。
库水位波动也是影响滑坡稳定性的一个重要因素。一方面库水位上升导致滑面岩土体被库水淹没,抗剪强度降低,滑坡稳定性降低,累计位移增大;另一方面库水位下降时所产生的渗透压力和孔隙水压力,使得滑坡下滑力增加,变形加剧。如在2013年6月,月降雨量58.1 mm,与5月累计降雨量56.3 mm接近相等,但该月的位移增加速率急剧增加到12.15 mm。一个可能原因是在5月到6月期间三峡水库水位平均下降了约10 m,导致滑坡体发生较大变形,累计位移突然增大。
目前月平均降雨量(R1),连续两月累计降雨量(R2),前后三个月平均降雨量(R3),月库水位变化最大量(W1)、平均月库水位(W2)等诱发因素常被用于滑坡预测[20]。灰色系统理论[21]是1982年由邓聚龙创立的一门边缘性学科,灰色关联分析是灰色系统理论的一个重要分支,被广泛用于计算滑坡诱发因素与滑坡位移间关联性的强弱。灰色关联分析一般分为三个步骤:①对原始数据列初值化处理;②求关联系数;③求关联度并排关联序列。利用位移速率的聚类分析结果和滑坡诱发因素构建灰色关联分析的子母矩阵,采用极差变化对数据进行归一化处理。将归一化处理后的结果代入公式(3),计算得到关联系数矩阵。最后利用公式(4),求解得到各个影响因子的关联度。

(3)
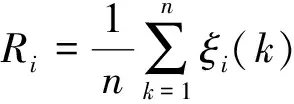
(4)
式中:ξi(k)——关联系数;
A(k)——降雨历时因子归一化后矩阵;
Bi(k)——其他影响因子归一化后矩阵;
ρ——分辨系数,一般计算中常取ρ=0.5;
Ri——各个影响因子的关联度。
计算得到各个诱发因素关联度分别为0.75,0.73,0.73,0.70,0.53。当诱发因素与滑坡位移关联度超过0.6,认为该因素对滑坡变形有着较强的控制作用。由于平均月库水位(W2)关联系数小于0.6,因此剔除平均月库水位诱发因素,则影响该滑坡的诱发因素为月平均降雨量(R1)、连续两月累计降雨量(R2)、前后三个月平均降雨量(R3)和月库水位变化最大量(W1)。
需对数据进行预处理。利用前文两步聚类分析结果和所确定的诱发因素代入随机森林模型对阶跃型滑坡变形阶段进行判定。以80%的原始数据作为模型的训练集,余下20%数据作为测试集检测模型的准确度。
在Matlab2014b平台编写随机森林算法,随机森林中决策树的初始参数设置为1 000棵,属性值设为1,即每次只采用一个属性对滑坡变形阶段进行判定。将训练集60个数据输入随机森林模型,然后利用测试集19个数据对模型进行检验。模型训练集和测试集运行结果见表3和表4。表3表明训练集45个稳定变形和15急剧变形点全部预测成功;表4表明测试集18个稳定变形点有2个预测失败,1个急剧变形点预测成功,测试集整体预测准确率达89.5%。综合测试集和训练集预测结果,得到模型整体预测结果(表5)。表5表明63个稳定变形点中,61个稳定变形点被预测成功,2个稳定变形点被预测成急剧变形点。16个急剧变形点全部预测成功,预测正确率达100%,模型总体预测正确率达97.5%。表明随机森林对滑坡变形阶跃点判定具有较好的适用性。

表3 ZG110随机森林模型训练集计算结果

表4 ZG110随机森林模型测试集计算结果

表5 ZG110随机森林模型整体计算结果

图6 ZG110随机森林模型整体预测结果图Fig.6 Overrall prediction results of random forest model of drill ZG110
第29和48月次,即2012年9月和2014年4月数据预测出现错误(图6)。前文已经叙述,随机森林通过投票对分类问题进行解答,为了分析误差出现的原因,调用随机森林算法中投票算法对结果进行进一步的判定。在利用随机森林对2012年9月进行分类时,共有7棵决策树认为该点为稳定点,993棵决策树判定该点为急剧变形点。同理,对2014年4月进行判定时22棵决策树判定为稳定点,978棵决策树判定该点为急剧变形点。上述数据表明,在利用随机森林对这两个数据点进行判定时,超过97%的基学习器(判别树)均出现了错误。对比分析2012年9月和2014年4月及其相邻月份的诱发因素,发现虽然该点的平均降雨量和月间库水位变化量与急剧变形位移点的诱发因素差距很大,但该点的累计降雨量和前三月平均降雨量与急剧变形点相似。因此,我们认为原始数据集数量不足和噪声是导致该数据点预测错误重要原因。
3 适用性验证
为了验证基于集成学习的阶跃型滑坡变形判定方法的适用性,选用八字门滑坡中与ZG110钻孔相同时间段的ZG111钻孔滑坡位移时间曲线进行验证。由于ZG111钻孔与ZG110钻孔均位于八字门滑坡体上(图2),因此滑坡诱发优势因素彼此相同,因此不再重新计算诱发因素与滑坡位移之间的关联系数。首先,对ZG111钻孔位移进行处理获得位移增加速率。然后利用两步聚类分析对滑坡位移增加速率进行分类,获得滑坡稳定变形点和滑坡急剧变形点。最后,将聚类分析结果作为随机森林模型输出项,优势诱发因素作为随机森林输入项建立阶跃型滑坡变形判定模型。滑坡累积位移—时间曲线和聚类分析结果见图5。由图5和聚类分析结果可知,其中共有63个稳定变形点和16个急剧变形点。16个急剧变形点中有8个变形点为组外变形点,并且与ZG111组外变形点完全重合。
由于滑坡各个部位的岩土体物理性质的差异性,如变形模量、含水率和重度等,使得滑坡各个部分的变形对降雨和库水位等诱发因素响应不同,导致组内阶跃点将会出现差异。但在极端工况下,滑坡体整体将会出现显著性变形,此时,坡体各个部分变形趋势趋于一致。因此,滑坡任意位置处的变形曲线应均能反应出此次极端事件信息。通过两步聚类分析算法对不同钻孔位移曲线进行分类,得到的组外阶跃点相同,表明聚类分析算法在确定滑坡分类上具有较好的适用性。
将ZG111钻孔两步聚类分析结果和优势诱发因素组合代入随机森林模型,模型预测结果见表6、表7和表8。由表6和表7知,本文建立的阶跃点模型预测准确率均达90%以上。预测模型不仅仅在训练集表现出较好的预测性能,并且在测试集中也展现出了卓越的预测性能。由表8可知,本文所建立的预测模型对实际稳定变形预测准确率达95%以上,对急剧变形点正确率超过93%,综合预测准确率近95%,表明模型有较好的适用性,整体预测结果见图7。

表6 ZG111随机森林模型训练集计算结果

表7 ZG111随机森林模型测试集预测结果Table 7 Prediction results of testing set for random forest model of drill ZG111

表8 ZG111 随机森林模型综合预测结果

图7 ZG111随机森林模型整体预测结果图Fig.7 Overrall prediction results of random forest model of drill ZG111
4 结论
针对阶跃型滑坡阶跃点难以判别的问题,本文采用聚类分析结合随机森林算法,建立了基于多场信息的阶跃型滑坡阶跃变形判别模型,并利用八字门滑坡ZG110和ZG111钻孔验证该模型的正确性。取得如下结论:
(1)提出了基于聚类分析的阶跃型滑坡阶跃点的识别模型,通过人工校核比对,发现该模型对识别阶跃型滑坡阶跃点的准确率近100%。
(2)利用灰色关联法确定了滑坡诱发优势组合,结合聚类分析结果,建立基于集成学习的阶跃型滑坡滑坡阶跃点判别模型,并对钻孔ZG110的阶跃点进行判别。模型整体预测正确率达97.5%,表明模型对阶跃型滑坡阶跃点具有很好的预测效果。
(3)通过八字门滑坡ZG111位移数据对该模型进行验证,模型整体预测正确率达94.9%,表明模型有较好的适用性,可为阶跃型滑坡预测提供参考。
