例谈连接体的速度求解问题——以绳、杆模型为例

(江苏省启东中学,江苏 南通 226200)

在高中力学教学中，常常会出现连接体问题，即两个物体通过轻绳、轻杆等进行连接，呈现出相互牵连的状态。这类运动形式不同于一般的动力学连接体，运用牛顿运动定律求解比较复杂，甚至无法求解，大多数情况下可以对连接体的运动效果进行分解，或者从功能角度进行求解，数理基础较强的学生还可以尝试采用微元法进行处理。这类问题的解题关键就是准确找出两物体间的速度牵连关系，从整体与微元两方面寻找问题隐含的数量关系。

1 运动效果分解法

例1：如图1所示，小车A与物体B通过轻绳连接，绳子穿过一定滑轮。若小车的运动状态为向左做匀速运动，其运动速度为v0。当小车运动到绳子和水平面成θ角时，物体B上升的速度为多少(忽略滑轮与轻绳之间的摩擦阻力)？

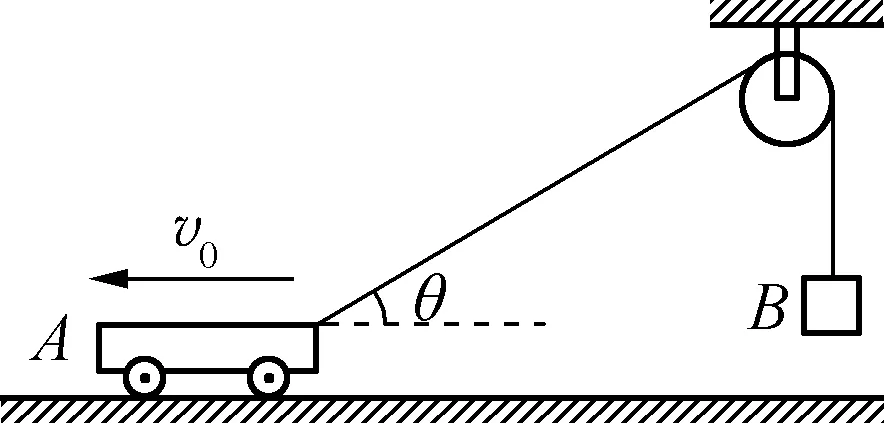
图1

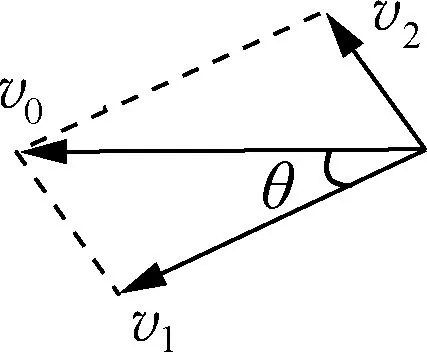
图2

在解决运动的合成与分解问题时，最重要的步骤就是准确地判断问题对象的合运动，分析清楚运动状态所表达的实际意义，然后借助运动分解等常规的力学方法进行计算。在该系统中，小车A向左运动的方向就是系统合运动的速度方向，这一合速度产生了两个运动效果：第一个效果就是使得物块B向上抬升，第二个效果就是使得绳子绕定滑轮顺时针方向摆动。

因此，将小车的速度v0分解为沿绳子方向的速度v1与垂直于绳子方向速度的v2(如图2)，结合平行四边形定则可知：物体B的上升速度v1=v0cosθ。

2 微元法

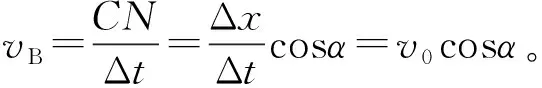
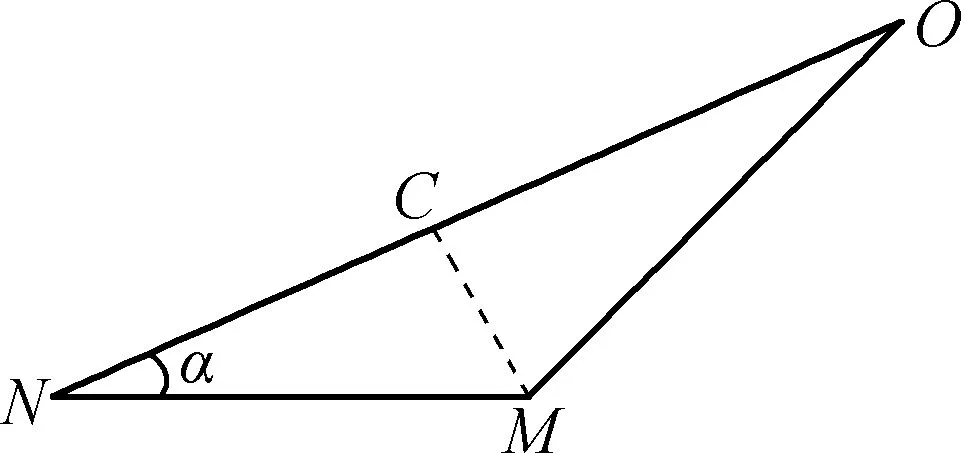
图3

微元法是一种数学方法，在物体的运动过程中，这种方法能揭示“运动效果分解”的本质，在物理中的运用常与三角函数结合，是一种常用的解题方法。

3 功能关系法

例2：如图4所示，小车A与小车B通过轻绳连接，小车A的运行速度vA是5m/s，当A端的绳子与水平面成30°，B端的绳子与水平面成60°，试求小车B的运行速度vB。

图4

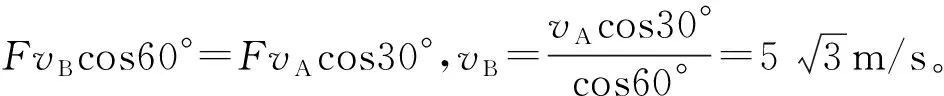
功能方法实际上是从功能角度对“运动效果分解法”的解读，在具体的问题情境中常常与功能关系、动能定理等联系起来。

4 相对运动法

例3：如图5所示，轻杆被竖直固定，上端固定一质量为m的小球，下端与质量为M的斜面相接触，接触点为A，斜面倾角为θ。当杆从A滑行距离L后到达B点，不计摩擦阻力，求这时斜面的速度。

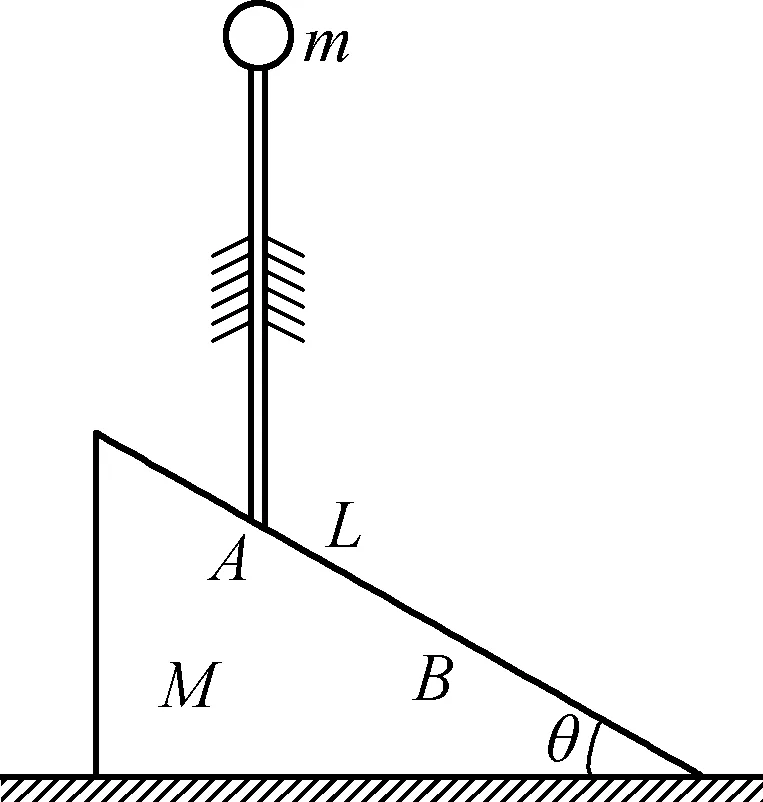
图5

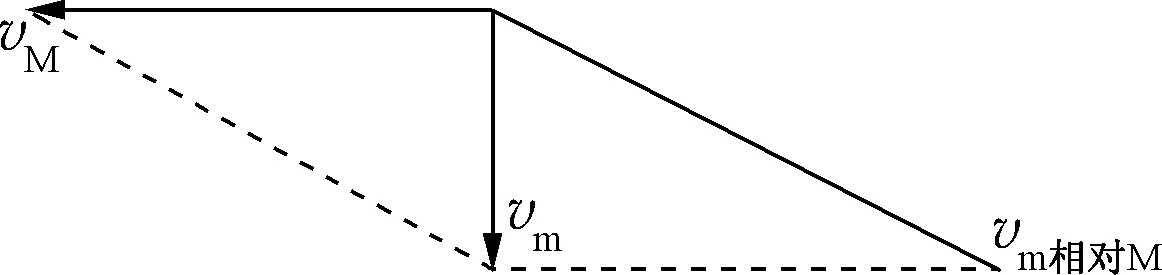
图6

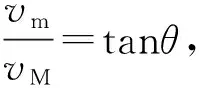
在连接体运动速度的求解问题中，往往存在相对的运动特征，因此借助相对运动法以及运动分解、三角函数等基本的数理方法，能够在相关的速度之间建立等式关系，那么系统内部各主体的运动速度就能够求解出来了。

5 速度投影方法

5.1 原理介绍

在同一时刻，做平面运动的刚体上任意两点速度在两点连线上的投影相等。

证明：假设A、B是刚体上的任意两点，A点速度为vA，B点速度为vB(如图7)。结合刚体性质可知：刚体上质元间距离不变，这就说明质元A、B沿两点连线方向的速度分量大小相等，即满足：v1=v2。

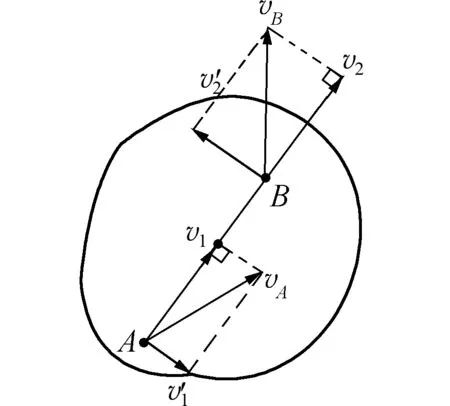
图7

5.2 例题与求解

例4：如图8所示，A、B为两根长度相等的刚性细杆，长度为L，两细杆一端共同与质量为m的球形铰链相连接，A杆另一端与质量为m的小球相接，B杆另一端与质量为2m的小球相接。将两杆靠拢，受到轻微触动后两球向两侧滑动，系统始终保持位于竖直平面内。不计杆的质量以及系统摩擦阻力，试求当两杆夹角为直角时A杆上球的运动速度。

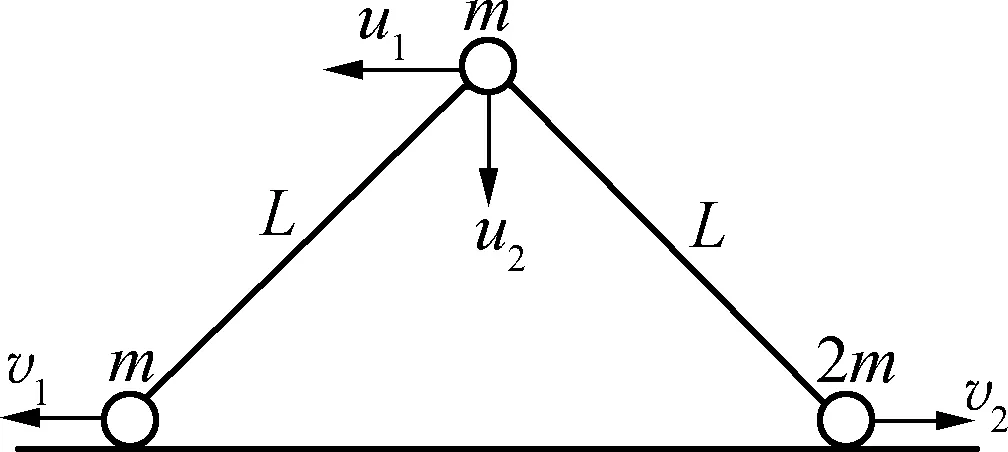
图8

假设A杆小球速度为v1，B杆小球速度为v2，铰链的水平速度为u1，竖直速度为u2。易知：系统水平方向动量守恒，因此：mv1+mu1=2mv2。同时，系统满足机械能守恒，那么：

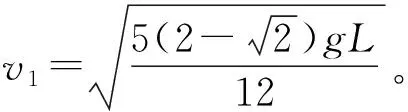
在解决连杆问题时，如果题目中明确给出为“硬性杆”“刚性杆”等条件时，需要利用速度投影定理，建立速度之间的等量关系，再结合题目的受力、功能关系等寻找其他的数量关系，最终求解出题目需要的速度值。

6 结语

本文结合具体例题，简介了实际教学过程中解决连接体问题的5种常用方法，基本涵盖了绳、杆牵连物体的速度求解问题。教师在教学过程中需要引导学生多角度地思考与分析问题，避免所有问题一律采用“受力分析——合成分解”这一常规方法，提高解答此类问题的准确率，培养学生灵活运用知识的能力。