动态矩阵控制在三自由度直升机中应用研究
2019-09-05方力智
方力智
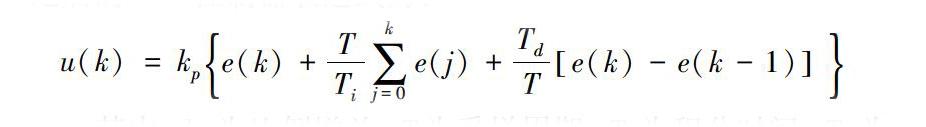
摘要:本文主要研究的是动态矩阵控制在三自由度直升机系统中的应用问题,将在基于三轴数字PID控制器的基础上,对俯仰轴以及旋转轴进行动态矩阵控制来优化系统的响应。
关键词:三自由度直升机系统;三轴数字PID控制;动态矩阵控制
作为一种可以在部分特性上仿真直升机的控制系统,三自由度模拟飞行姿态系统[1]被众多控制技术学者关注并研究。它自身的多输入多输出特性、强耦合特性和强非线性特性,决定了它是一个控制工程中的难控制对象。本文研究预测控制在三自由度模拟飞行姿态系统中的应用,即将其简化为一个弱耦合、若非线性的系统,在其上应用预测控制。
1 控制方法
1.1控制方法
控制律的设计主要采用闭环控制。考虑到1、本文所研究的动态矩阵控制需要基于渐近稳定的系统,所以需要对该系统先进行内环调稳;2、另外考虑到本文要将该控制律应用到实际系统当中,将选取容易实现且鲁棒性好的PID控制器作为系统内环控制器。在内环系统使用PID控制器调稳之后,再加入外环的动态矩阵控制以优化控制性能。
1.2控制系统结构
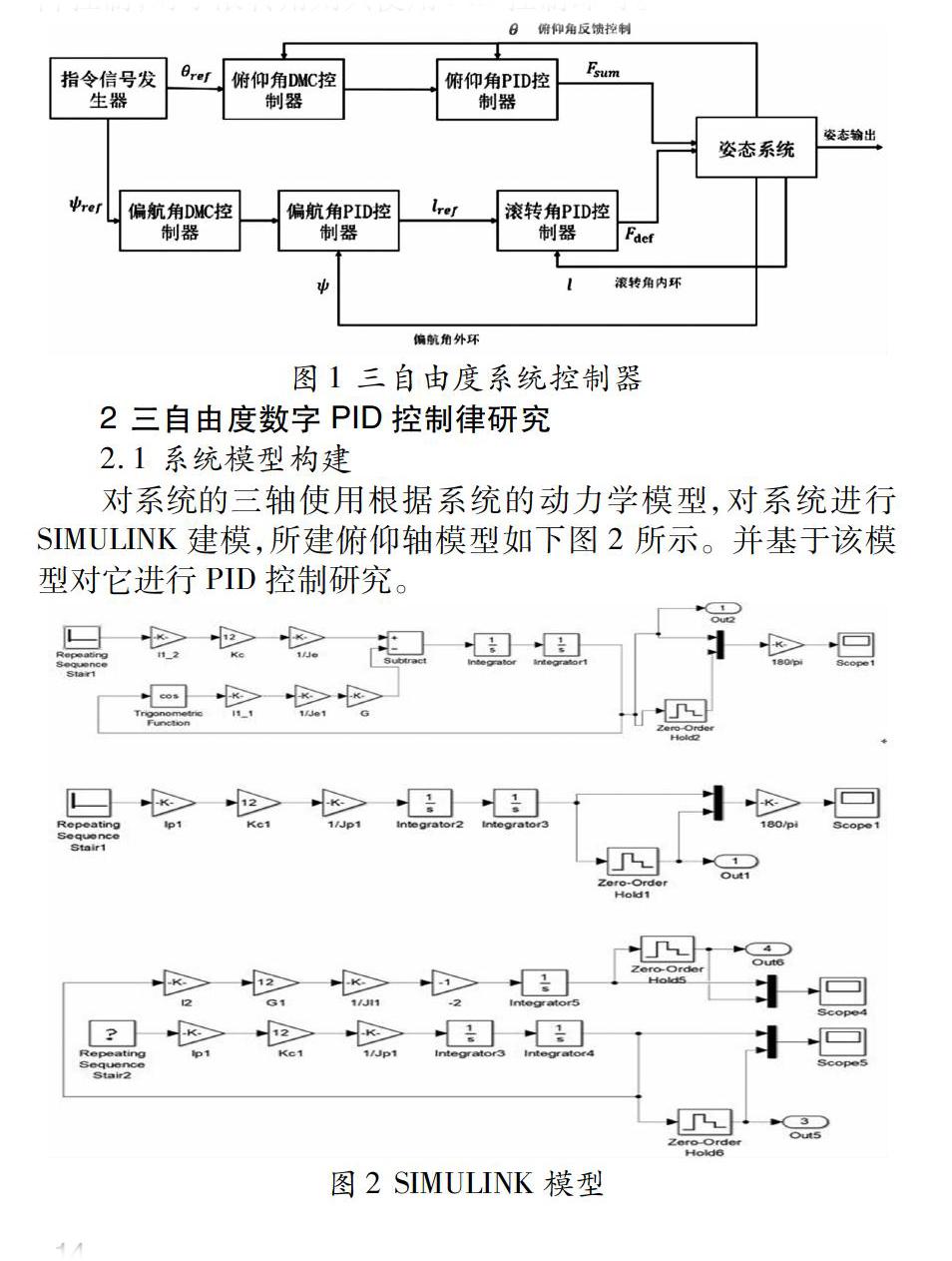
原本的系统对于俯仰轴以及滚转轴依然有着一定的耦合性,通过引入两个新的控制量 ,把该系统分解成两个互不相关独立的控制通道,俯仰运动和偏航运动。而偏航运动由滚转运动和偏航运动两个部分组成,滚转轴的滚转运动将直接影响到偏航运动。下图2-1表示整个系统的控制流程,对于主控对象俯仰角及偏航角采用内环PID控制加上外环动态矩阵控制,对于滚转角则只使用PID控制即可。
2 三自由度数字PID控制律研究
2.1系统模型构建
对系统的三轴使用根据系统的动力学模型,对系统进行SIMULINK建模,所建俯仰轴模型如下图3-1所示。并基于该模型对它进行PID控制研究。
2.2数字PID控制简述
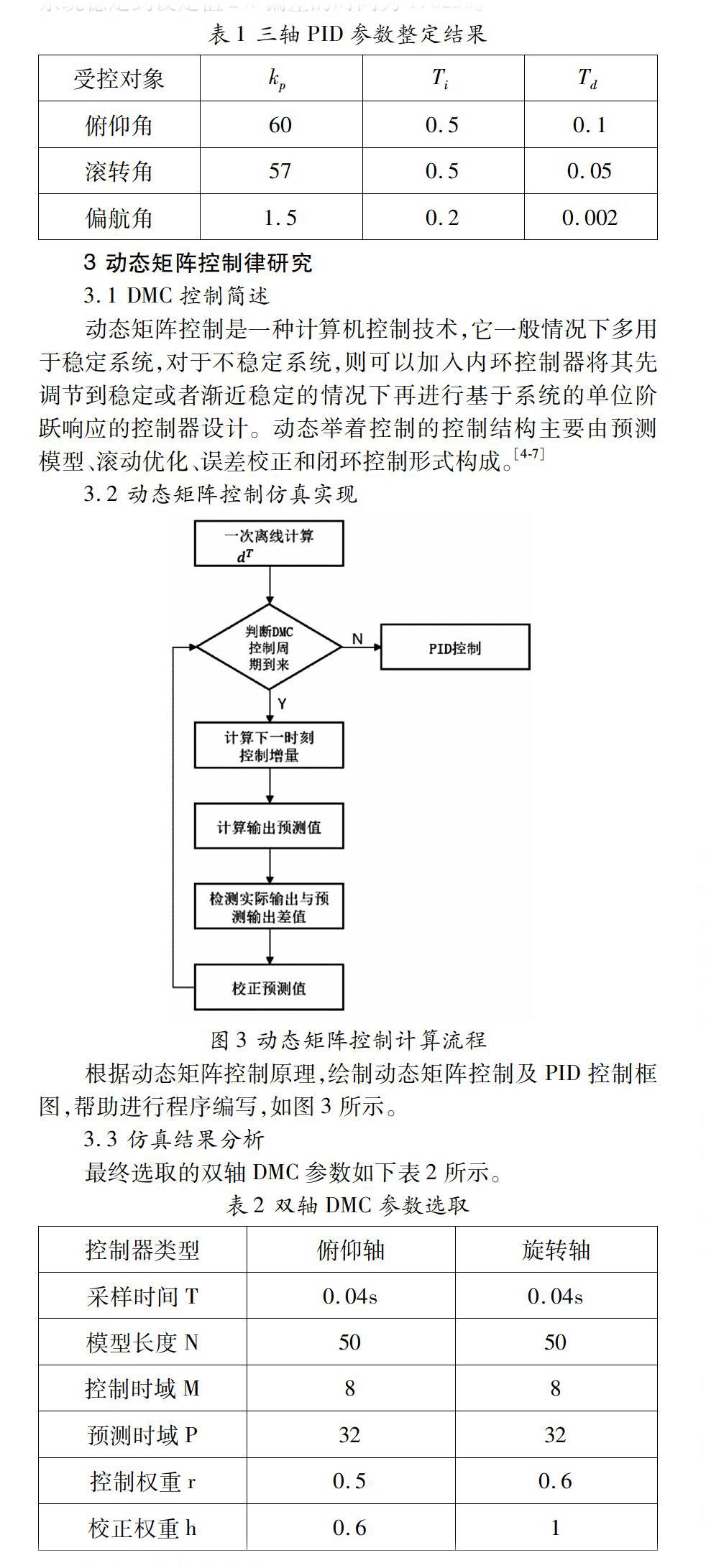
在实际电控系统中,用的都是传感器的采样数值进行控制,而新的控制量也是基于不同采样时刻的偏差值计算出来的。所以在这里,需要对该系统进行离散化PID控制,离散化之后的PID控制器表达式为:
其中, 为比例增益, 为采样周期, 为积分时间, 为微分时间, 为为了更加逼近实际系统的作动过程,对于三轴的连续系统,将使用Simulink进行建模仿真,而对于其控制部分,将使用M函数进行数字PID控制的实现。
2.3 PID参数整定
PID控制器参数整定表示的是确定了控制器为PID形式之后,通过调节 等控制器中的参数,使得控制回路的动态特性及静态特性能满足期望的指标,从而达到理想的控制目标。PID控制方法当然也有着自己的局限性和缺陷。它控制的模型必须保证系统参数不会随着时间变化。并且,PID参数整定出来的算法,每一次整定出来的解都只不过是局部优化解,并不是全局最优值。所以,只需要找到局部最优解,使它满足指标要求即可。本次研究使用的PID参数整定方法为扩充临界比例度法[2]:首先选择一个足够短的采样周期 ;在仿真运行的时候,只使用比例系数 ,用一开始选定的采样周期 ,慢慢增大比例系数 的数值,直到系统出现等幅度震荡的时候,记录下当前 值,当前的临界震荡周期也记录下来;根据齐格勒-尼克尔斯提供给的经验公式,计算得到不同类型的控制器的控制参数。
2.4 数字PID仿真结果
在用临界比例度法调节完三个轴上的PID的时候,曲线的线型已经十分接近想要的结果,但是结果并不能直接达到满意的效果。于是考虑在已有的PID情况下进行微调。微调则是参考经验试凑法[3]进行即可。一般情况下,增大比例系数 能够减小偏差,并同时减弱系统中负载的扰动效果,但同时它会加强测量噪声对系统的影响,而当 增幅过大时,它极有可能使系统变成不稳定系统;积分控制器调控的是过去的偏差量,其主要作用是消除系统中的静差,减小 会增大系统超调,但是增大它又会导致系统的稳定时间下降,需根据实际情况慢慢调试;微分控制器是对过去偏差的差值进行调控,换句话说,就是对误差的变化率进行调控,有一定的预测功能,增大 值能加快系统的响应时间,但是如若 过大,会让控制对象变成不稳定系统。
最终对于仿真模型调整的三轴PID参数如下表3-1所示。其中俯仰轴的过冲17.11%。系统稳定到设定值2%偏差的时间为0.355s;横侧轴的峰值振幅为1.0743,过冲7.43%。系统稳定到设定值2%偏差的时间为0.160s;旋转轴和横侧轴有着很大的耦合关系,需要建立在横侧轴PID整定调稳之后,进行旋转轴PID调节;旋转轴的峰值振幅为1.2791,过冲27.91%。系统稳定到设定值2%偏差的时间为1.025s。
3 动态矩阵控制律研究
3.1DMC控制简述
动态矩阵控制是一种计算机控制技术,它一般情况下多用于稳定系统,对于不稳定系统,则可以加入内环控制器将其先调节到稳定或者渐近稳定的情况下再进行基于系统的单位阶跃响应的控制器设计。动态举着控制的控制结构主要由预测模型、滚动优化、误差校正和闭环控制形式构成[4-7]。
3.2动态矩阵控制仿真实现
根据动态矩阵控制原理,绘制动态矩阵控制及PID控制框图,帮助进行程序编写,如图4-1所示。
3.3仿真结果分析
最终选取的双轴DMC参数如下表4-1所示。
3.4双轴控制性能
使用MATLAB进行控制器设计及仿真实验。下图4-2中,(a)图和(b)图为最终用DMC改进之后的俯仰轴及旋转轴控制效果,可以看出加入了DMC控制的系统快速性和稳定性都相对于只使用PID控制器的系统更加良好。
(a)俯仰角
(b)偏航角
4 结论
本文针对三自由度直升机简化后的弱耦合、弱非线性模型进行了预测控制器的设计,在内环上分别对三个轴使用了PID控制器,使用MATLAB对其仿真实现,再调处良好稳定效果之后,在俯仰轴以及旋转轴的外环上加入了动态矩阵控制以优化控制性能。并用MATLAB结合SIMULINK進行仿真实现,最终得到了相较于只使用PID控制器的系统而言,更为良好的控制效果。
参考文献
Shan J, Liu HT, Nowotny S.Synchronised trajectory-tracking of multiple 3-DOFexperimentalhelicopters. IEEE Proceedings-Control Theory and Applications, 2005, 152(6):683-692.
于明星, 王瑛, 邵帅. 基于Matlab的临界比例度法在工程PID参数自整定数值模拟中的应用[J]. 辽宁师专学报(自然科学版), 2018, v.20;No.78(02):11-13+19.
刘鑫. 三自由度直升机实验系统控制策略的研究[D]. 东北大学, 2008.
铉佳欢. 动态矩阵预测控制的PLC实现及工业应用[D].
席裕庚, 耿晓军, 陈虹. 预测控制性能研究的新进展[J]. 控制理论与应用, 2000, 17(4):469-475.
席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3):222-236.
李小鹤. 广义预测控制简化算法的研究与分析[D]. 华北电力大学(保定).
