直线超声电机非线性建模及控制*

李志亮，肖文磊，赵 罡

(北京航空航天大学 机械工程及自动化学院，北京 100191)

0 引言

直线超声电机是一种新型的微特电机，它利用压电材料的逆压电效应，激发压电振子在超声频段内产生微小振动，并通过摩擦作用将压电振子的微观振动直接转换为动子的直线运动，驱动负载[1]。与传统电磁电机相比，直线超声电机具有体积小、响应速度快、不受电磁干扰、控制精度高等优点，同时直线超声电机驱动平台不需要传动机构便可直接驱动负载，断电后保持自锁，无回程误差，因此直线超声电机在微型机械、精密定位等领域得到广泛的应用[2]。

直线超声电机压电材料的能量转换过程、机械能的摩擦传递过程以及驱动电路中的电量变化过程都使得其具有明显的非线性，同时温度的变化也会导致谐振频率的漂移。由于诸多能量转换过程中的非线性以及使用环境中的不确定性，造成了难以对直线超声电机进行精确的数学建模[3-4]。因此，目前常用的直线超声电机控制多采用无模型的控制方法，例如PID控制、模糊控制、自适应控制、非线性补偿控制、神经网络控制等。其中，节德刚等采用模糊PID控制法，使超声电机达到较高的定位精度[5]；Mo J S等使用自适应控制算法进行位置控制，补偿非线性的同时解决了时变问题[6]；Liang W等使用PID结合非线性补偿的方法，提高了位置控制精度[7]；王寿健等采用BP神经网络控制方法提高了超声电机的控制精度和响应速度[8]。但是由于缺少数学模型的约束，这些控制方法难以针对直线超声电机的特点进行针对性的优化，不能充分发挥直线超声电机的性能，限制了其精度的进一步提高。因此，一直以来都有人不断尝试对直线超声电机进行建模，主要包括等效电路模型和机理模型。其中，史敬灼等建立了超声电机压电振子的等效电路模型，并且辨识出压电振子的等效参数值[9]，Zhang X L等基于哈默斯坦模型建立了带死区的直线超声电机模型[10]，但是机理模型参数较多，模型复杂，难以直接用于直线超声电机的控制。

上述学者的研究均采用无模型的控制方法对超声电机进行控制，取得了不错的控制效果，但是由于没有数学模型的约束，控制精度难以进一步提高；部分学者也对超声电机进行了建模，其中等效电路模型的等效参数辨识可用于指导超声电机的结构设计以及工作特性分析，却难以直接应用于超声电机的控制，机理模型由于模型参数多，同样难以直接应用于控制。针对以上问题，本文尝试建立一种简单实用的直线超声电机非线性模型，在该数学模型的基础上，设计非线性补偿PID算法，对直线超声电机进行定位控制，最后通过实验对该定位控制算法进行验证。

1 直线超声电机的非线性建模

建立精确的数学模型是对直线超声电机进行高精度控制的基础，近年来，国内外许多研究人员在直线超声电机的建模上做了很多工作，建立的直线超声电机数学模型包括等效电路模型和机理模型，其中等效电路模型结构简单，模型参数少，易于实现，是研究直线超声电机机电耦合特性的一种简单有效的方式。

直线超声电机的等效电路模型，即将直线超声电机定子的质量、阻尼等效为合适的电子元件，利用电学网络来分析直线超声电机特性，从而使用电学中的非线性理论来对电机的非线性进行研究，为电机控制方法提供参考。目前确定直线超声电机等效电学参数有两种方法：参数辨识法[11]和直接测量法[12]。参数辨识法是通过测量可测参数，根据理论分析和实验测量辨识出未知等效参数，这种方法实验简单，参数辨识结果准确。直接测量法，如导纳圆测量法，该种方法实验复杂，误差较大。本文采用参数辨识法来辨识直线超声电机等效电路模型的参数。直线超声电机为容性负载，为简化计算，将直线超声电机等效为电容进行分析。图1所示为直线超声电机及驱动电路模型，其中R为驱动电路的等效电阻，L为驱动电路的匹配电感，C为驱动电路的匹配电容。驱动电路输入为占空比可调的功率方波，功率方波在LC匹配电路和电机等效电容共同作用下产生具有一定电压增益的正弦波，输出正弦波驱动电压。

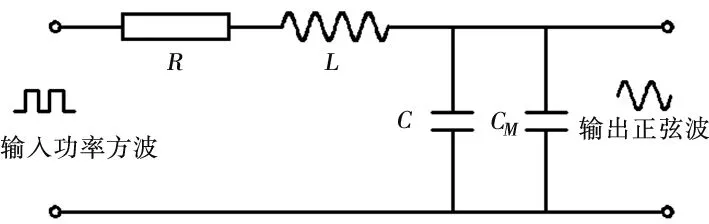
图1 直线超声电机及驱动电路模型

直线超声电机的功率主要由功率方波的一次谐波控制，因此对功率方波进行傅里叶变换，提取一次谐波作为输入，示波器采集的输出电压作为输出。

已知驱动电路中功率方波电压峰值U=±48V，方波频率f=48500Hz，匹配电感L=5.7×10-4H，匹配电容C=1.57×10-8F。式(1)为提取方波信号的一次谐波峰峰值，其中μ为功率方波占空比，式(2)为电路模型的增益，式(1)与式(2)相乘可得理论输出正弦波电压的峰峰值UO，如式(3)所示。通过实验测得驱动电压峰峰值为UO′。

(1)

(2)

UO=A·|G(s)|

(3)

结合理论电压UO与实测电压UO′，使用最小二乘法辨识参数CM和R。等效电路模型辨识拟合曲线如图2所示。

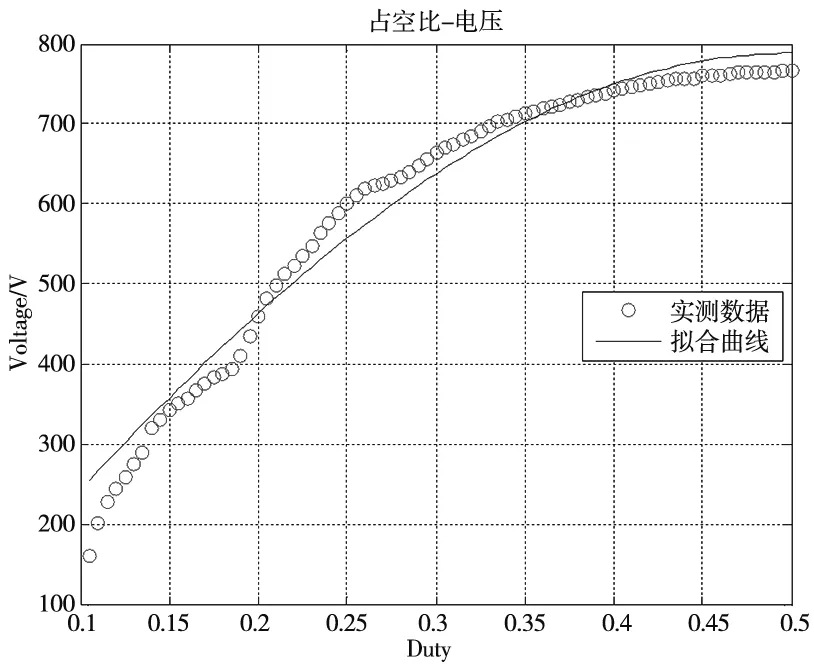
图2 等效电路模型辨识拟合曲线

在电压值为610V～640V时，速度变化存在明显的拐点，因此采取分段多项式拟合电压—速度曲线。设正、负向目标多项式函数分别为y1和y2，如式(4)和式(5)所示，其中x为驱动电压峰峰值，y1和y2为平均速度。

(4)

(5)

结合实验测量的电压峰峰值数据UO′与平均速度数据V，使用最小二乘法辨识分段多项式系数。拟合结果如图3所示，图3a为驱动电压峰峰值与正向平均速度的拟合曲线，图3b为驱动电压峰峰值与负向平均速度的拟合曲线。

(a) 正向运动

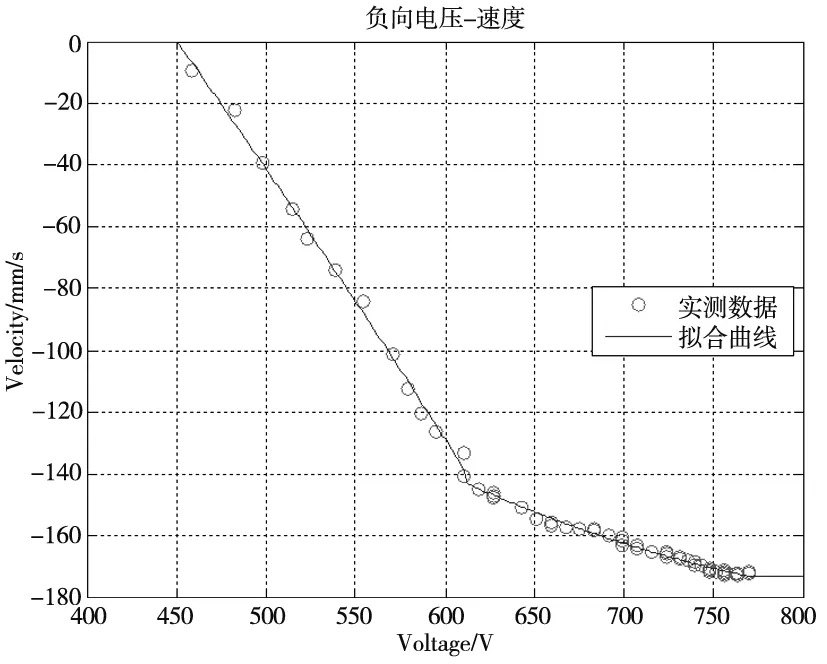
(b) 负向运动 图3 驱动电压峰峰值与平均速度拟合曲线

图4所示为建立的直线超声电机非线性模型，其中μ为占空比，fNL1为占空比μ与PWM功率方波一次谐波峰峰值的非线性关系，Uin为PWM功率方波一次谐波峰峰值，Uout为驱动电路输出电压峰峰值，fNL2为驱动电压峰峰值与平均速度的非线性关系，V为直线超声电机的平均速度。

图4 直线超声电机非线性模型

2 定位控制算法及仿真

针对超声电机的非线性问题，史敬灼等基于建立的哈默斯坦非线性模型采用多步预测自校正控制方法控制超声电机的转速[13]；肖莹等基于辨识模型采用内膜控制PID算法，补偿了超声电机的非线性，对外界干扰有良好的适应性[14]；黄鲁江采用基于逆系统的非线性预测控制，取得了良好的控制效果[15]。这些非线性补偿控制方法中，自校正控制、非线性预测控制算法较为复杂，实现难度较大，而通过逆模型补偿非线性是一种简单有效的非线性补偿算法，结合PID控制，可以很好补偿直线超声电机的非线性。因此本文根据直线超声电机的非线性模型，采用求逆模型的方法进行非线性补偿，然后进行PID定位控制，由于不同误差下要求控制器具有不同的性能，因此采用分段PID进行控制，当误差小于1μm时，PID控制器输出为0，停止控制。

(a) 非线性补偿PID控制方法框图

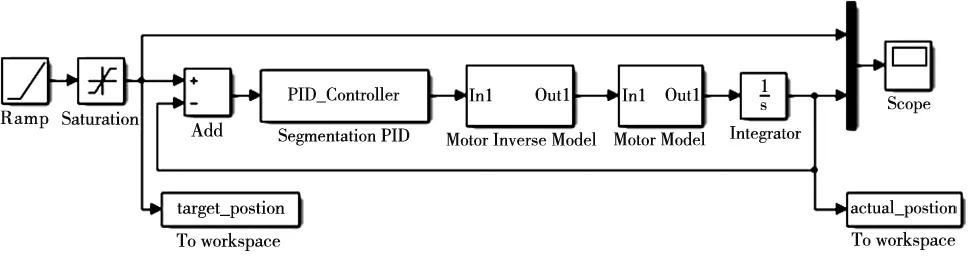
(b) 非线性补偿PID控制方法仿真框图图5 定位控制算法框图及仿真框图

仿真系统中设定目标位置为2mm，在0.1s时产生斜坡位置信号，仿真结果如图6所示。

图6 定位控制仿真结果

3 定位控制实验及分析

3.1 实验平台简介

非线性补偿PID定位算法通过Simulink仿真验证后，还需通过定位实验进一步验证，因此搭建支持EtherCAT协议的实验系统。EtherCAT协议是一种基于以太网的实时工业现场总线通信协议，它具有通信效率高，时钟精度高的优点，可实现很小的同步周期，非常适合高性能直线超声电机的控制。该实验平台包括以下主要设备：笔记本电脑，伺服驱动器，直线超声电机定位平台。其中笔记本电脑运行TwinCAT 3软件作为主站；直线超声电机伺服驱动器作为从站，通过EtherCAT协议与主站通信；精密定位平台作为控制对象，平台采用海德星HF1直线超声电机驱动，安装有光栅尺用于反馈位置信息。控制系统示例图如图7a所示，实物图如图7b所示。

(a) 控制系统示例图

(b) 控制系统实物图 图7 控制系统结构图与实物图

3.2 定位控制实验

在以上实验平台进行定位实验，设定目标位置为20mm，以10mm/s的定位速度执行定位过程，实测位置、速度、占空比曲线如图8所示。由曲线可知，速度波动较小，定位过程较为顺畅，最终定位精度较高。

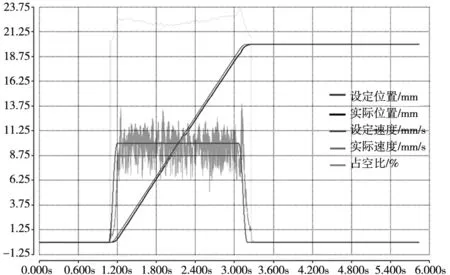
图8 定位过程位置、速度、占空比曲线

设定不同目标位置，以不同的定位速度进行定位控制，定位误差绝对值如表1所示。多次重复实验，均可达到同样的控制效果，定位误差绝对值小于1μm。

表1 定位误差表

4 结论

本文基于建立的直线超声电机非线性模型，设计非线性补偿PID算法，并对该算法进行仿真和实验，证明了其有效性。重复定位实验结果显示，该算法可以实现定位误差小于1μm的控制效果，在微型机械、精密定位等领域有一定的实用价值。