基于格子玻尔兹曼方法的化学驱色谱分离机制
2019-09-05杨圣贤郭振海张广福王惠宇杜庆军
杨圣贤, 郭振海, 张广福, 王惠宇, 杜庆军
(1.中国石化胜利油田分公司胜利采油厂,山东东营 257051; 2.中国石油大学(华东)石油工程学院,山东青岛 266580;3.非常规油气开发教育部重点实验室, 山东青岛 266580)
化学复合驱技术是油田提高采收率的重要方法。化学复合驱油体系是多组分溶质(一般采用几种化学剂的复配),构成该体系的各组分分子结构千差万别,渗流过程受到注入速度、自身化学性质以及地层性质等方面的影响[1-2],在运移过程中出现一定程度的分离,在渗流路径上表现为具有一定的流过次序,而非同时流过,即色谱分离现象[3-4]。色谱分离现象的存在,使化学剂在地层运移过程中的浓度比例与地面实验室配置的质量浓度比例不尽相同,导致复合体系配方发生改变,驱油效果不能达到最佳[5]。因此在研究和筛选复合驱化学剂的配方时,也应考虑不同化学剂的物性差异。目前,实验室内可以准确测量出色谱分离发生的程度[6],但是对于色谱分离发生过程中,各组分在填充细管和地层中的分布难以确定。现有的数值模拟方法包括蒙特卡罗方法、分子动力学方法等微观模拟手段[7],但主要用于流体相平衡尺度的研究;宏观数值模拟难以表征化学剂色谱分离机制。格子玻尔兹曼方法作为一种基于分子动力学理论的介观模拟方法[8-9],具有物理背景清晰、理论严谨等特点,能够准确模拟流动的过程中对流、扩散和滞留等过程[10]。笔者采用格子玻尔兹曼方法,考虑多组分化学剂在多孔介质中渗流的路径运移差异、扩散运移差异、竞争吸附等机制特征,建立化学驱色谱分离模拟方法,并认识色谱分离机制及其主控因素。
1 化学剂渗流格子玻尔兹曼模型
假设:二维多孔介质模型包含固体颗粒与孔隙两部分,孔隙中流体均匀分布,温度保持恒定;化学复合驱体系由两种表面活性剂组成,且两者之间不发生化学反应;化学剂随流体流动,且扩散过程为均匀扩散,各方向的扩散系数相同;化学剂分子在介质表面发生吸附与解吸,但不发生滞留。
1.1 格子玻尔兹曼方法
1.1.1 流体对流方程
流体对流的格子玻尔兹曼模型中的分布函数的演化方程[11]表示为
fi(x+eiΔt,t+Δt)-fi(x,t)=Ωi.
(1)
式中,ei为第i个方向的离散速度;fi为粒子速度分布函数;Δt为时间步长;Ωi为碰撞项。
采用D2Q9离散速度模型,具有9个方向粒子速度:
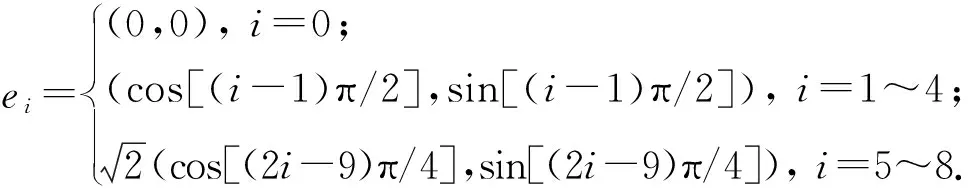
(2)
采用多松弛时间(MRT)模型计算多孔介质中流体对流。对流过程的MRT模型的演化过程则可以表示为
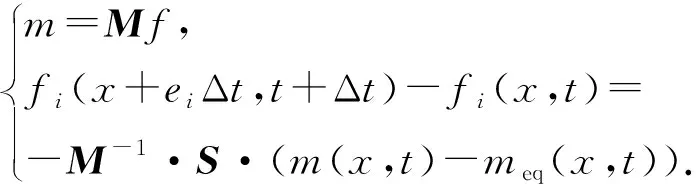
(3)
式中,M为变换矩阵;S为对角矩阵;m为矩空间的分布函数。
以上LBM模型可以通过多尺度展开还原为N-S方程,流体宏观密度ρ和流动速度u表达式分别为

(4)

(5)
1.1.2 化学剂对流扩散方程
采用单松弛时间(LBGK)模型中的D2Q5模型计算化学剂溶质扩散,扩散过程的LBGK模型的演化方程表示为

(6)
其中
式中,gi(x,t)为质量浓度分布函数;geqi为平衡分布函数;τ为松弛时间。
1.1.3 竞争吸附方程
化学剂之间的竞争吸附采用Langmuir等温吸附式描述。假设表面活性剂A与表面活性剂B在颗粒表面发生竞争吸附。某一时刻,颗粒表面的总面积为1,表面活性剂A所占面积比例为θA,表面活性剂B所占比例为θB,则未吸附区域所占面积比例为1-θA-θB。此时,表面活性剂A和B的吸附速率分别为
vaa=kaaca(1-θA-θB),
(7)
vab=kabcb(1-θA-θB).
(8)
式中,vaa和vab分别为表面活性剂A和B的吸附速率;kaa和kab分别为表面活性剂A和B的吸附速率常数;ca和cb分别为表面活性剂A和B在液固界面的质量浓度。
表面活性剂A和B的脱附速率分别为
vda=kdaθA,
(9)
vdb=kdbθb.
(10)
式中,vda和vdb分别为表面活性剂A和B的脱附速率;kda和kdb分别为表面活性剂A和B的脱附速率常数。
表面活性剂A和B的吸附量分别为
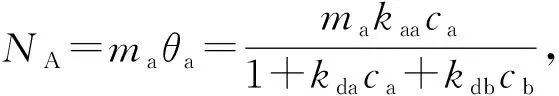
(11)

(12)
式中,NA和NB分别为表面活性剂A和B的吸附量;ma和mb分别为表面活性剂A和B的最大吸附量。
1.2 边界条件的处理
格子玻尔兹曼方法的边界处理方式众多,化学驱渗流模拟边界条件包括液固接触表面和注入端部位[12-14]。本文中采用标准反弹边界处理液固接触,该格式假设粒子与壁面发生碰撞后沿相反的方向弹回;入口端则采用恒定速度和恒定化学剂质量浓度边界处理,出口端采用充分发展条件。
化学剂渗流的关键边界条件为吸附边界,吸附过程中,溶质的质量浓度在边界满足

(13)
其中
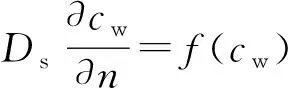
如图1所示,以底面边界为例,此时溶质速度分布函数迁移后未知量为g2,吸附边界条件的插值形式为
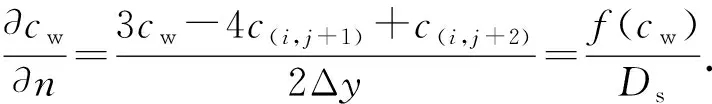
(14)
进一步得到g2为
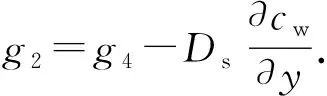
(15)
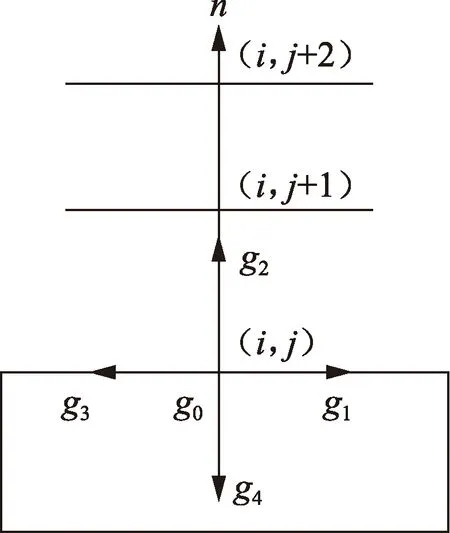
图1 吸附边界示意图Fig.1 Schematic diagram of adsorption boundary
1.3 模型求解及验证
对于所建立的化学剂渗流格子玻尔兹曼模型,采用数值方法进行求解:将实际数据转换为格子单位数据;采用格子玻尔兹曼方法对多孔介质中流体的流动过程进行模拟,以获取流动场的相关数据;对化学剂对流扩散过程进行求解,获取表面活性剂的质量浓度场数据;对多孔介质表面的竞争吸附过程进行计算,获取化学剂在介质表面的吸附量等相关数据;同时统计产出质量浓度和吸附量随时间的变化曲线。
进一步利用二维平板内考虑单边吸附(下平板)的传质扩散方程解析解验证边界条件的正确性,该方程的解析解为Lévêsque Solution[13],其表达式为
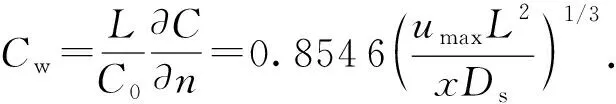
(16)
式中,L为平板宽度;Cw为壁面吸附量;C0为入口吸附量;umax为最大流速;x为距离入口的距离。
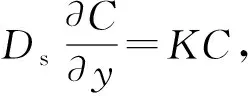

图2 吸附边界格式验证Fig.2 Verification of adsorption boundary
2 化学驱色谱分离机制及实例计算
2.1 化学驱色谱分离机制
化学驱色谱分离的机制众多,包括竞争吸附、离子交换、液液分配、多路径运移及滞留损失等。假设:多孔介质中的流体均匀分布,表面活性剂在油水两相中的分配无差异;此外,不考虑离子与表面活性剂间的反应及化学剂的滞留。因此本文中化学驱色谱分离的主要机制为路径运移差异、扩散运移和竞争吸附。
(1)路径运移差异。路径运移差异一般是指由于多孔介质中孔隙分布的随机性,在注入体系流动的过程中,在不同的位置上会有不同的流动速度。对于同一种物质,由于多孔介质中的运移路径的不同,相同物质的产出时间也会出现差异,在主流线上,流动距离较短,流速较快,经主流线的物质可以较早的产出;而对于其他流线上的物质,流动长度增加,流速减慢,导致产出时间较晚。图3为多孔介质和不含多孔介质环境下的流场对比。可以看出,多孔介质的存在改变了流线方向,使多孔介质各处的流动速度存在差异,造成表面活性剂的流动存在差异,在出口端的产出出现先后顺序,从而产生色谱分离现象。
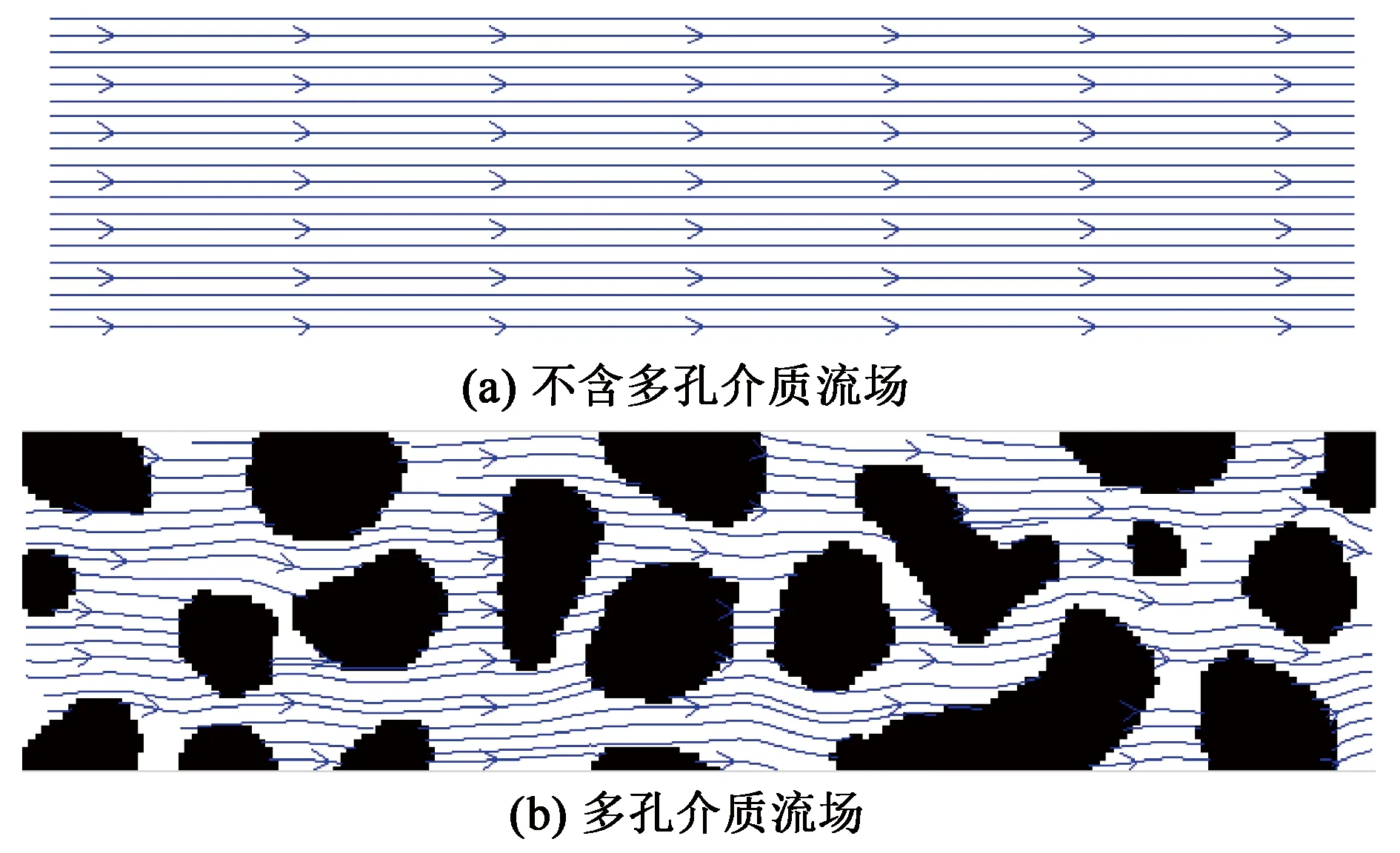
图3 路径运移流线对比Fig.3 Streamline comparison of path migration
(2)扩散运移差异。不同表面活性剂由于自身质量浓度差异也会造成分布差异,由于质量浓度梯度而出现的自发扩散也会造成两种表面活性剂的色谱分离现象。不考虑扩散过程条件下,表面活性剂到达出口端与表面活性剂完全排出的时刻会出现生产曲线突变,两种物质的生产曲线完全重合,因此不会发生色谱分离的现象;考虑扩散过程条件下,两种表面活性剂的生产曲线在出口端不会发生生产曲线突变,而是平滑的曲线。实际油田化学驱开发过程中,多种表面活性剂的物理性质会有差异,扩散系数也会有不同,在相同的时间内,扩散系数较大的物质扩散范围较大,首先到达出口端,导致两种表面活性剂发生色谱分离现象。
(3)竞争吸附。吸附过程是表面活性剂在多孔介质中流动与多孔介质表面由于发生化学、物理反应而滞留于多孔介质表面的过程。此外由于不同种类的表面活性剂自身在结构上的差异,导致其在多孔介质表面的吸附能力存在着较大的差异。竞争吸附则是由于多种物质在多孔介质表面进行吸附时所发生现象,与非竞争吸附相比,竞争存在则会减小物质的吸附量。吸附过程的存在对于表面活性剂突破时间和最高质量浓度对应时间影响较小,但对质量浓度分布区间和最高质量浓度影响较大。这主要是由于发生吸附时,孔隙中表面活性剂的质量浓度减小,而且竞争吸附过程的表面活性剂的吸附量会小于非竞争吸附过程,造成的孔隙中表面活性剂的减小值大于非竞争吸附过程,导致质量浓度曲线中无吸附过程最高质量浓度值大于竞争吸附过程的最高质量浓度。
2.2 色谱分离实例模型建立
基于二维多孔介质刻蚀模型进行图像分割,作为流动模拟的多孔介质基础模型。模拟过程中入口端为恒定流速恒定质量浓度注入,出口端为充分发展边界,液相与固相接触面的液体流动过程与表面活性剂扩散过程采用反弹格式。注入过程中,先注入水驱替0.5VP,然后注入表面活性剂A和B的溶液0.5VP,最后再进行后续水驱。基础模型中格子长度为1×10-5m,时间步长取1×10-3s,注入速度为1×10-5m/s,注入液黏度为1×10-5m2/s。表面活性剂A的注入质量浓度为1 g/L,扩散系数为2×10-9m2/s,最大吸附量为2.0 mg/g,平衡常数为12;表面活性剂B的注入质量浓度为1 g/L,扩散系数为3×10-9m2/s,最大吸附量为6.0 mg/g,平衡常数为6。
2.3 色谱分离质量浓度场分布及产出曲线特征
图4为注入1.0VP和2.0VP时多孔介质内部表面活性剂A和B的质量浓度场分布,其中左侧为注入段,右侧为产出端。可以看出,在注入1.0VP时,两种表面活性剂质量浓度场分布基本一致;随着注入时间的增加,化学剂溶液在多孔介质中受到岩石颗粒的阻挡作用,产生液固界面作用,两种表面活性剂吸附和扩散差异加大。注入2.0VP时,进入后续水驱阶段,表面活性剂A质量浓度高于B,但流动速度稍慢。

图4 不同时刻两种表面活性剂质量浓度分布Fig.4 Mass concentration distribution of two surfactants at different time
定义相对质量浓度为产出质量浓度与注入端质量浓度的比值。图5为表面活性剂产出相对浓度随注入孔隙体积倍数(VP)的变化。可以看出,由于两种表面活性剂自身化学性质的差异,导致产出化学剂发生了色谱分离现象。为定量表征色谱分离程度,以表面活性剂B产出曲线为例,定义无因次突破时间t0为化学剂产出相对质量浓度大于0.001时的注入孔隙体积倍数,作为化学剂开始产出的标志;无因次质量浓度分布区间T为产出曲线上相对质量浓度大于0.2的注入孔隙体积分布区间,表征化学剂的分散程度;无因次质量浓度峰值Cmax为产出相对浓度的最高值;无因次质量浓度峰值时刻tm为无因次质量浓度峰值对应的注入孔隙体积倍数。
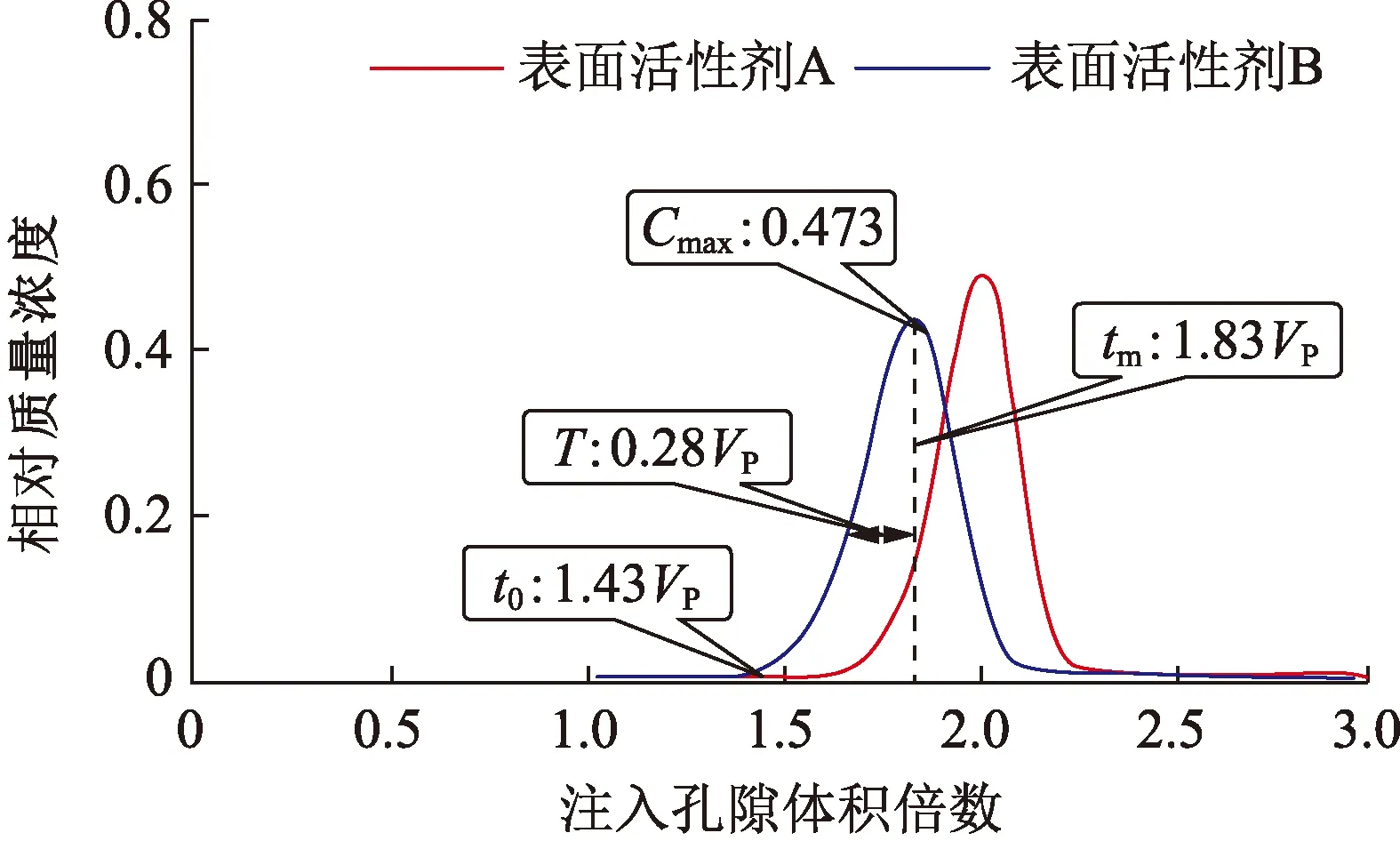
图5 表面活性剂产出相对质量浓度的变化 Fig.5 Change of relative mass concentration of surfactant
从图5可以看出,表面活性剂B无因次突破时间比A早,且表面活性剂B的无因次质量浓度分布区间比A大,表明表面活性剂B前缘运移速度快,扩散程度大;无因次质量浓度峰值差异反映了两种表面活性剂扩散和吸附的综合影响。色谱分离现象主要由扩散和运移的差异导致。
图6为两种表面活性剂在多孔介质表面的吸附量随注入孔隙体积倍数的变化。可以看出,注入化学剂溶液开始阶段,表面活性剂A和B吸附量随注入孔隙体积倍数的增加而增加,后续水驱阶段解吸速度高于吸附速度,吸附量降低;表面活性剂A的最高吸附量远低于B。
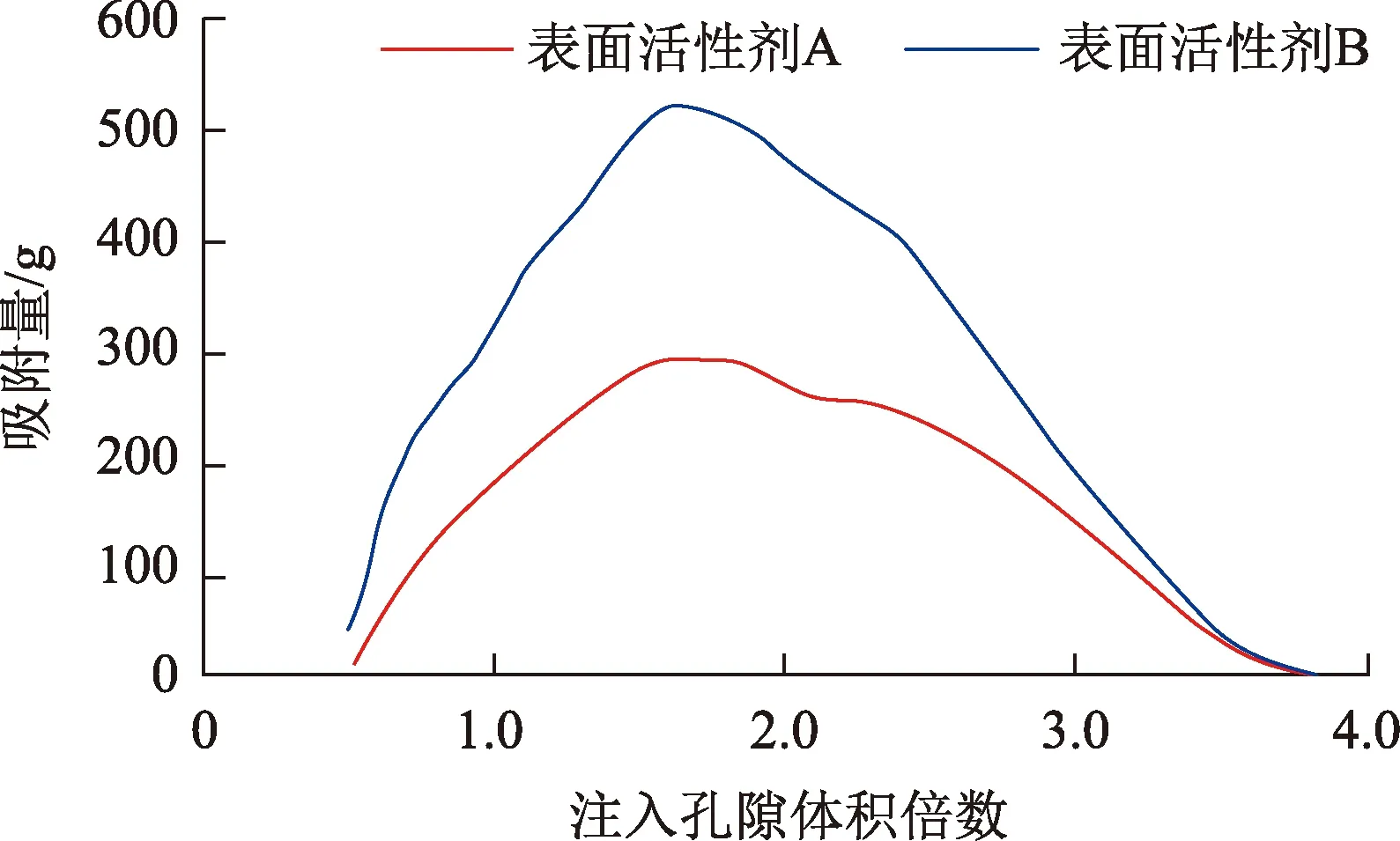
图6 表面活性剂吸附量的变化Fig.6 Change of surfactant adsorption capacity
3 化学剂色谱分离影响因素
基于色谱分离定量表征指标,通过两种表面活性剂的无因次突破时间差和无因次质量浓度峰值差分析色谱分离程度的影响因素,并确定主控因素。
3.1 注入速度
不同注入速度对色谱分离程度的影响见图7。随着注入速度的增加,无因次突破时间差值减小,无因次质量浓度峰值差值增大。这是由于随注入速度增加,表面活性剂扩散程度减小,两者差异缩小;但注入速度增加,导致相同时间内表面活性剂的有效注入量会增加,从而导致最高质量浓度差值增加。

图7 不同注入速度下各参数的差值Fig.7 Difference of parameters at different injection velocities
3.2 流体黏度
不同注入流体黏度对色谱分离程度的影响见图8。随着注入黏度的增加,无因次突破时间差与无因次质量浓度峰值差均减小,即两种表面活性剂的色谱分离程度减小。这是由于随着注入体系黏度的增加,表面活性剂在多孔介质扩散时遇到的阻力增大,两种表面活性剂的扩散过程都受到了抑制,导致表面活性剂段塞的扩散范围减小,色谱分离的程度逐渐减小。
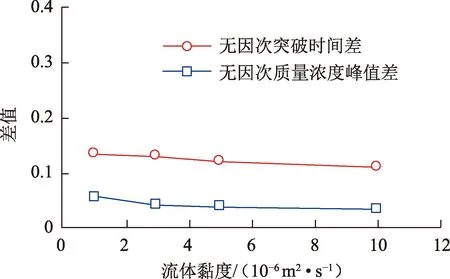
图8 不同流体黏度下各参数的差值Fig.8 Difference of parameters at different viscosity
3.3 扩散系数
保持表面活性剂A扩散系数不变,改变表面活性剂B扩散系数进行计算。不同扩散系数对色谱分离程度的影响见图9。随扩散系数增大,无因次突破时间差与无因次质量浓度峰值差均增大,即两种表面活性剂的色谱分离程度增加。这是由于随着表面活性剂B扩散系数的增加,使表面活性剂B的扩散范围增大,无因次突破时间提前,但相应的无因次质量浓度峰值降低,两种表面活性剂无因次质量浓度峰值差值增大。
3.4 最大吸附量
保持表面活性剂A最大吸附量不变,改变表面活性剂B的最大吸附量取值。最大吸附量对色谱分离程度的影响见图10。随着表面活性剂B最大吸附量的增加,无因次突破时间差基本不变,但无因次质量浓度峰值差大幅增大。主要是由于最大吸附量不会对注入体系的流动过程产生影响,但化学剂吸附后,会影响流体的质量浓度。
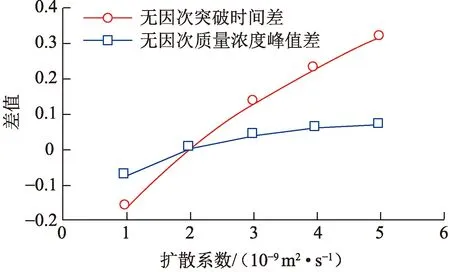
图9 不同扩散系数下各参数的差值Fig.9 Difference of parameters at different diffusion coefficient

图10 不同最大吸附量下各参数的差值Fig.10 Difference of parameters at different maximum adsorption capacity
3.5 平衡常数
保持表面活性剂A的平衡常数不变,改变表面活性剂B平衡常数取值。平衡常数对色谱分离程度的影响见图11。随着平衡常数的增加,无因次突破时间差与无因次质量浓度峰值差均无变化,即色谱分离程度不受平衡常数的影响。这是由于竞争吸附过程中平衡常数对于注入体系的流动过程不会产生影响。

图11 不同平衡常数下各参数的差值Fig.11 Difference of parameters at different equilibrium constant
3.6 色谱分离主控因素

(17)
其中
式中,n为数据序列个数;yi为第i个数据值。
CV反映了一组数据分散和差异程度,CV越大说明该数据序列数据间差异程度越大;反之,数据越集中。在色谱分离影响因素分析中,CV值表征色谱分离对各因素敏感程度。
分别统计计算不同影响因素对无因次突破时间差和无因次质量浓度峰值差的敏感程度,结果如图12所示。可以看出,在讨论的参数取值范围内,色谱分离现象中,无因次突破时间差的主控因素是扩散系数和注入速度;无因次质量浓度峰值差的主控因素是最大吸附量和扩散系数。
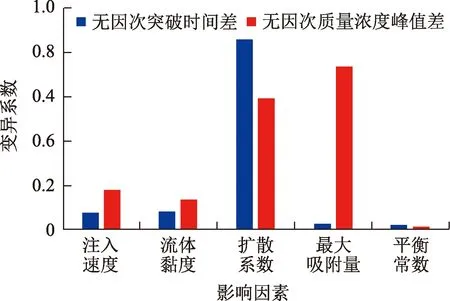
图12 不同影响因素敏感性分析Fig.12 Sensitivity analysis of different influencing factors
4 结束语
采用格子玻尔兹曼方法,考虑流体对流、化学剂扩散及竞争吸附特征,综合固液表面及注采端边界条件,建立了多孔介质多组分化学剂色谱分离模拟方法。 以两种表面活性剂溶剂为例,模拟得到化学驱色谱分离产出曲线及多孔介质中化学剂质量浓度分布规律,发现色谱分离的主要机制为渗流的路径运移差异、扩散运移差异、竞争吸附等。扩散系数和注入速度是无因次突破时间差的主控因素,最大吸附量和扩散系数是化学剂无因次质量浓度峰值差异的主控因素。
