郫都区大型超市共同配送中心选址模型的建立与求解

2019-09-05何凌四川托普信息技术职业学院经济管理系

消费导刊 2019年35期

何凌四川托普信息技术职业学院经济管理系

一、引言

近年来，随着经济的发展和城市范围的拓展，越来越多的居民选择在成都市三环路以外甚至四环路以外居住。郫都区由于距离成都市中心较近，地铁、公交、自驾出行都比较方便，教育资源丰富等原因，居住人口逐渐增多。各大品牌的连锁超市也选择在该区域选址开店，目前已有永辉超市4家、沃尔玛2家、步步高1家。但是其均采取自营采购和门店配送的模式，不仅需要配备车辆，还要运营配送中心，成本较高，也对该地区交通状况造成了影响。如实施共同配送，成本会得到大幅度降低。

二、建立共同配送中心的意义

共同配送是美国、日本等一些发达国家采用较广泛、影响面较大的一种先进的物流方式，我国在2012年开始在各个城市试点推广共同配送。其本质是由多个企业采取多种方式，对物流配送各要素上的各个企业的横向集成，实现商品配送的共同化和物流设施及网络资源的共享化，具有良好的社会和经济效益。

按照具体的组织形式，共同配送可分为系统优化型和设施利用型。郫都区大型超市实施共同配送属于同产业之间的联合，既可以采用系统优化型，也可使用设施利用型。本文建议采用配送设施利用型，其关键点是为各大超市建立共同配送中心，由共同配送中心负责为其向制造商、批发商共同进货；制造商和批发商将商品送至共同配送中心；由共同配送中心负责验货、保管、分拣；再向各大超市门店进行共同配送。

三、共同配送中心选址模型的建立

考虑到郫都区范围内大型超市目前的具体数量不多及分布的地理位置距离不远，有一个配送中心即可完成相应的业务，因而本文采用精确重心法建立选址模型。该模型需要考虑的选址因素有郫都各区超市之间的距离、各超市与待建配送中心之间的运费率、各超市的配送需求量等具体信息。

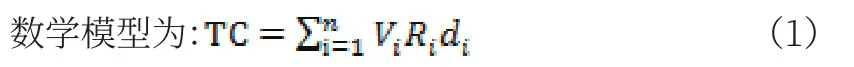
式中，TC——总配送成本；

Vi——i点的配送量；

Ri——i点到选址点的配送费率；

di——从位置待定的共同配送中心到i点的距离。

本文按照以下步骤建立数学模型：

（一）建立坐标系，在百度地图中任选一点作为原点，建立二维坐标系，吉选超市郫县店、吉选超市恒创蜀都店、永辉超市万达店、永辉超市时代豪庭店、步步高超市红光店、永辉超市时代天街店、沃尔玛中海国际店、吉选超市犀浦店、沃尔玛红光店这九个超市用A（ii=1，2，3…9）表示。使用百度地图的测距工具，测量每个超市到坐标轴的直线里程；再将每个超市到坐标轴的直线里程按照1公里换算为1单位坐标轴的标准刻度，即可确定各超市的二维坐标，xi分别为：3.5、4.5、5.4、5.1、8.6、6.9、12.4、12、8.9；yi分别为10.5、9.5、10.3、8.4、6.4、4、0.718、4.8、7.4。

（二）调查各超市的运输需求量

郫都区的各大超市都位于居住人口较为密集或者人流量较大的区域，每个超市每天的配送需求量不一致，按照每个超市所处的位置及调查情况，预估每个超市每天的需求量Vi分别为：2t、1.3t、4.2t、3.1t、3.1t、5.3t、6.3t、2.6t、4.2t。

（三）确定各超市的城市配送费率

各超市的城市配送运费率与超市周边交通状况、超市收货所需时间、超市运输需求量、使用配送车辆车型及配送距离等有关系，预估每个超市的配送费率Ri，分别为11.2元/t.km、10.5元/t.km、10.7元/t.km、10.3元/t.km、11.5元/t.km、10.9元/t.km、12.3元/t.km、10.2元/t.km、11.3元/t.km。

四、基于EXCEL的精确重心法求解

重心法手工计算求解较为繁琐，计算过程很容易出错，因此本文采取EXCEL进行求解。

（一）求初始解

将公式（1）求解可得到共同配送中心位置的初始坐标值。其重心的坐标为：

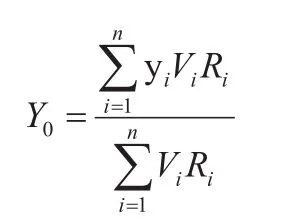
在Excel中建立表格，以计算X0，Y0，如图1所示，具体求解过程如下：

图1 使用Excel求解初始解示意图

①输入原始数据

在第1行从B列至H列，分别输入xi、yi、Vi、Ri、xiViRi、yiViRi、ViRi，在A列的第2行至第10行分别输入A1、A2、A3、A4、A5、A6、A7、A8、A9；在B列的第2行至第10行输入A1-A9的横坐标值；在C列的第2行至第10行输入A1-A9的纵坐标值；在D列的第2行至第10行输入A1-A9的每日配送需求量即Vi的值；在E列的第2行至第10行输入A1-A9配送费率即Ri的值；在E11输入求和符号Σ，即表示F12-H12需要对应的列第2行至第12行的和；在G12输入X0，表示H12为初始横坐标的值；在G13输入Y0，表示H13为初始纵坐标的值。

②求解X0和Y0

在F2单元格中输入公式“=B2＊D2＊E2”，即可求得x1V1R1，使用填充句柄，可求出F3至F10的值，在F11单元格使用自动求和公式，求出∑xiViRi；在H2单元格内输入公式“=D2＊E2”，即可求得R1V1，使用填充句柄进行向下填充，可求出H3至H10的值；在H10单元格输入公式“=SUM（H2:H10）”，即可求出∑ViRi；在H12单元格内输入公式“=F11/H11”，并将数据保留三位小数，即可求出X0。

在G2单元格中输入公式“=C2＊D2＊E2”，即可求得y1V1R1，使用填充句柄，可求出G3至G10的值，在G11单元格使用自动求和公式，求出∑yiViRi；在H13单元格内输入公式“=G11/H11”，并将数据保留三位小数，即可求出Y0。

从图3中可见，共同配送中心的初始坐标值（X0，Y0）为（8.250，5.839），显然该坐标值不是最优的值，因此还需要进行优化，优化过程使用精确重心法的迭代。

（二）使用精确重心法进行迭代，求解最优选址位置

①精确重心法的迭代过程及最优解判断标准

将公式（1）展开为具体的算式：V1＊R1＊d1+ V2＊R2＊d2+……Vn＊Rn＊dn。其中，，Xi，Yi为每个超市的坐标，Xn-1，Yn-1为上一次计算出的配送中心的坐标，由此得出坐标计算的公式：

将（2）中求出的初始坐标（X0，Y0）计算出di，将di代入上面的公式求出第一次计算出的坐标（X1，Y1）。反复迭代，计算di，直到某次配送中心的坐标与上一次坐标的差值小于0.1，即：ΔXn=|Xn-Xn-1|＜0.1且ΔYn=|Yn-Yn-1|＜0.1。这时停止迭代，得到配送中心的最佳选址位置为(Xn，Yn).若迭代超过6次仍然不满足小于0.1这个要求，就停止迭代，使用第6次的计算结果。

②使用Excel进行多次迭代：

具体求解过程如下：

第一次迭代求解的详细过程：

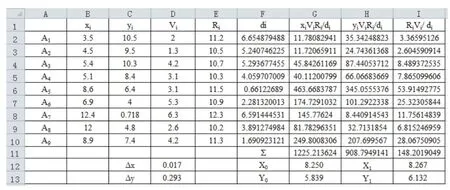
图2 第一次迭代计算的Excel计算表

按照图2所示建立第一次迭代计算表。将图3的Excel表格的A-E列复制于新表中，在E-I列的第一行分别输入单元格名称di、xiViRi/di、yiViRi/di、RiVi/di，在单元格F11输入求和符号“Σ”，表示G11-I11为对应列第2行至第10行的和；在F12中输入X0，F13中输入Y0，并在G12和G13中分别输入X0和Y0的值，即8.250和5.839，以便于计算di的值。在H12和H13中分别输入X1和Y1，表示I12为X1的第一次迭代值，I13表示Y1的第一次迭代值。在C12单元格输入Δx，并在D12中输入公式“=ABS（I12-G12）”，表示Δx的值；在C13单元格输入Δy，并在D13单元格中输入公式“=ABS（I13-G13）”，表示Δy的值，通过Δx和Δy判断该次迭代结果是否是最优解，将C12和C13单元格设置为保留三位或三位以上的小数，以便更好的进行判断。

在单元格F2中输入公式“=SQRT((B2-$G$12)^2+(C2-$G$13)^2)”，此单元计算d1的值，一定要注意将保存X0和Y0值的单元格进行绝对引用，以保证d2-d9单元格由该公式进行填充计算的准确性。在G2单元格输入公式“=B2＊D2＊E2/F2”，并向下填充至G9，求得xiViRi/di的值；在H2单元格输入公式“=C2＊D2＊E2/F2”，并向下填充至H9，求得yiViRi/di的值；在I2单元格输入公式“=D2＊E2/F2”，并向下填充至I9，求得RiVi/di的值。在单元格G11、H11、I11中分别使用自动求和公式，求出ΣxiViRi/di、ΣyiViRi/di、ΣRiVi/di的值。在单元格I12中输入公式“=G11/I11”，在单元格I13中输入公式“=H11/I11”，保留三位小数，即可求得第一次迭代值（X1，Y1），即（8.267，6.132）；同时在单元格D12和D13中也出现了Δx和Δy的值，即0.017和0.293，不满足ΔXn=|Xn-Xn-1|＜0.1且ΔYn=|Yn-Yn-1|＜0.1，因此需要再次进行迭代。

第二次迭代求解的详细过程：

将图2中X0和Y0分别改为X1和Y1，X1和Y1分别改为X2和Y2，再将G12和G13从X0和Y0的值分别改为X1和Y1的值，即将原表中的8.250和5.839分别改为8.267和6.132，数据改完以后，对应的值会发生变化，即可求出第二次迭代结果（X2，Y2）为（8.331，6.273），而Δx和Δy的值为0.064和0.141，不满足ΔXn=|Xn-Xn-1|＜0.1且ΔYn=|Yn-Yn-1|＜0.1，因此需要进行第三次迭代。

第三次迭代求解与第二次迭代的详细过程类似，此处不再累述，求解结果为（X3，Y3）=（8.390，6.335）；Δx=0.058，Δy=0.062，满足ΔXn=|Xn-Xn-1|＜0.1且ΔYn=|Yn-Yn-1|＜0.1，该次迭代结果为最优解。