基于灰色神经网络的云南省货运量预测模型研究
2019-09-05巫仁亮徐伟华沈文喆WURenliangXUWeihuaSHENWenzhe
巫仁亮,徐伟华,沈文喆 WU Renliang,XU Weihua,SHEN Wenzhe
(昆明理工大学 交通工程学院,云南 昆明 650500)
(Faculty of Traffic Engineering,Kunming University of Science and Technology,Kunming 650500,China)
0 引言
在规定的时间内输送的实际货物数量称为货运量,货运量能够反映一个地区的实际运输成果,也是反映一个地区实力强弱的重要指标。货运量的预测结果,能对云南省相关政策的制定与改革作出参考。目前文献对货运量预测的主要方法模型为灰色GM( 1,1)模型[1]、灰色马尔科夫链模型[2],多元线性回归模型[3]等,但这些方法模型没有自我学习,自我适应的能力,致使计算结果误差较大。本文收集了2008年到2018年云南省货运量及其影响因素的相关数据,建立GM(1,8)模型,采用灰色神经网络算法对云南省货运量进行预测。灰色神经网络结合了灰色系统理论与BP神经网络算法,具有自我学习与自我适应的能力,能不断修改误差,提高预测精确性。
1 灰色神经网络算法
1.1 灰色神经网络算法理论
灰色系统理论(Grey System Theory)不同于所有信息已知的白色系统和所有信息未知的黑箱系统,灰色系统是指“一部分信息知道,而一部分信息不知道”的不确定的,数据不足的系统。灰色系统是一种研究样本数据不足、信息不确定问题的新方法,由中国大陆邓聚龙教授在1982年提出。目前已广泛应用于经济指标、工业、社会、环境、农业等多种复杂的预测系统中[4]。
灰色神经网络模型(Grey Neural Network)有嵌入型、串联型、并联型和混合型四种结构。并联型与串联型灰色神经网络属于组合预测模型。相较于单独的灰色预测模型或者神经网络算法模型,并联型与串联型灰色神经网络具有更高的预测精确度。串联型灰色神经网络是先由灰色系统处理数据,再将处理后的数据交由神经网络处理。并联型灰色神经网络是灰色系统与神经网络同时对样本数据进行处理,再将处理后的数据进行整合。将灰色系统模型的预测结果结合其他特质,再经过神经网络算法的非线性拟合能力优化预测结果是嵌入型灰色神经网络。混合型灰色神经网络通过BP神经网络进行自学习与自适应调节灰色系统的各个参数,有线性和非线性两种结构[5]。
灰色系统模型拥有样本数据不足、信息不确定,没有自我学习、自我适应的能力和解决非线性问题能力弱的特点,样本数据的轻微变动就会导致整个灰色系统模型的重建。而BP神经网络模型是模仿生物神经元的工作模式,拥有样本数据充足,自我学习能力、自我适应能力与解决非线性问题能力强的特点[6]。灰色系统模型与BP神经网络模型相结合可以互相弥补不足,增强解决问题的能力。将灰色系统模型与BP神经网络模型相结合,利用它们各自的特点,建立拥有更强的稳定性、更高的预测精度、更快地处理问题速度的灰色神经网络预测模型[7]。
本文首先对数据进行处理,灰色系统模型再对处理后的数据建立样本,最后利用BP神经网络的自我学习与自我适应能力对样本数据进行预测。其过程为,先将数据分别进行归一化与累加处理,灰色系统再把处理的数据生成样本数据,将样本数据输入BP神经网络(Back Propagation Neural Network)进行训练,最后训练好的BP神经网络输出预测结果。
1.2 灰色神经网络模型
(1)根据灰色系统相关理论建立GM (1,n)模型
建立一个拥有n个输入变量,1个输出变量的多维灰色系统模型。
(2)对数据进行归一化处理
本文采用离差标准化方法,对原始序列B=(b1,b2,…,bn)进行变换。

(3)对归一化数据进行累加处理
A(1)为A(0)的累加序列:

(4)建立灰色微分方程
建立一个灰色神经网络模型的微分方程式为:

其中:c与d1,d2,…,dn为微分方程系数
式(3)的时间响应式为:
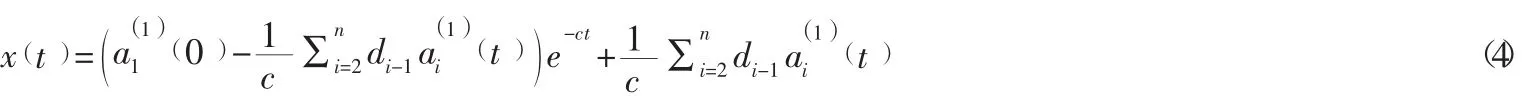

则式(4) 可转化为:
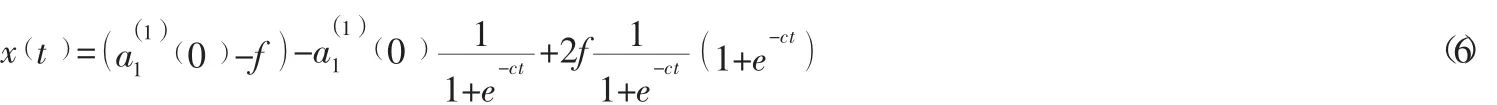
(5)将时间响应式映射到BP神经网络得到灰色神经网络
把式(6)映射如图1所示的已经扩展的BP神经网络中,建立GM (1,8)模型就会得到8个输入参数,1个输出参数的灰色神经网络。扩展的BP神经网络有8个输入节点,通过实验发现当隐含层神经元个数为4个时预测结果最精确。隐含层的刺激函数为S型正切函数,S型正切函数即sigmoid函数,sigmoid函数拥有单调递增和反函数单调递增的性质,其取值为(0,1)之间的任何数。输出层的刺激函数为purelin线性函数,purelin函数是线性传递函数,拥有输入等于输出的特征。训练函数为train函数,train函数是神经网络训练函数,它的功能是实现神经网络的自学习,自适应,不断更新神经网络参数,直到达到最小误差或者最大学习步数才停止更新神经网络参数。
1.3 灰色神经网络算法步骤
(1)利用训练数据初始化灰色神经网络的参数
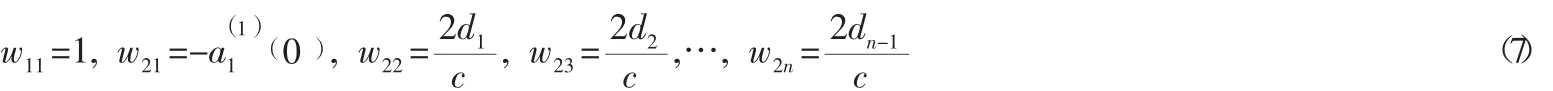
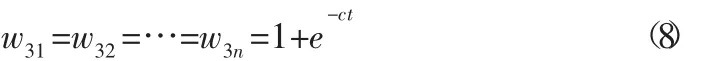
由阈值的定义设置LD层的阈值为:

(2)对每个训练数据,计算其各层的输出LA层的输出:
【编者按】周淑英,蔚县剪纸的第三代传人,国家级非物质文化遗产传承人,第十三届全国人大代表,联合国教科文组织授予她“中国民间工艺美术家”称号,她的作品《清明上河图》《百蝶图》《生命树》《鲤鱼跳龙门》《五牛神图》等多次获得国内外奖励并为中央美院、中国美术馆收藏。

LB层的输出:

LC层的输出:
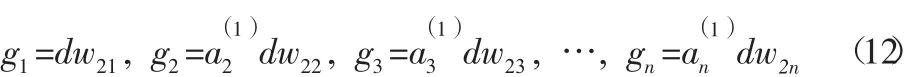
LD层的输出:
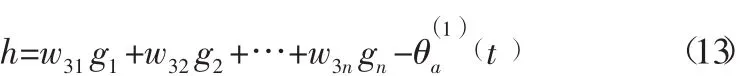
(3)计算灰色神经网络预测值与实际值之间的误差LD层的误差:

LC层的误差:
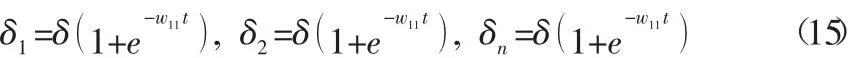
LB层的误差:
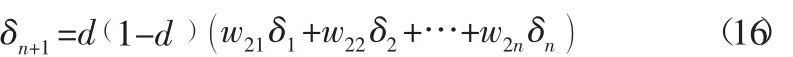
(4)根据预测的误差调节灰色神经网络的权值
LB层到LC层调节后的权值为:
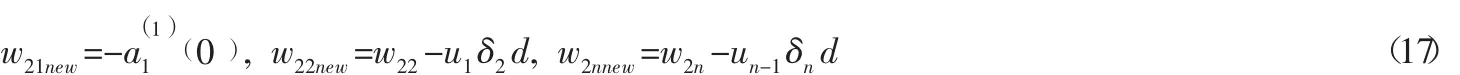
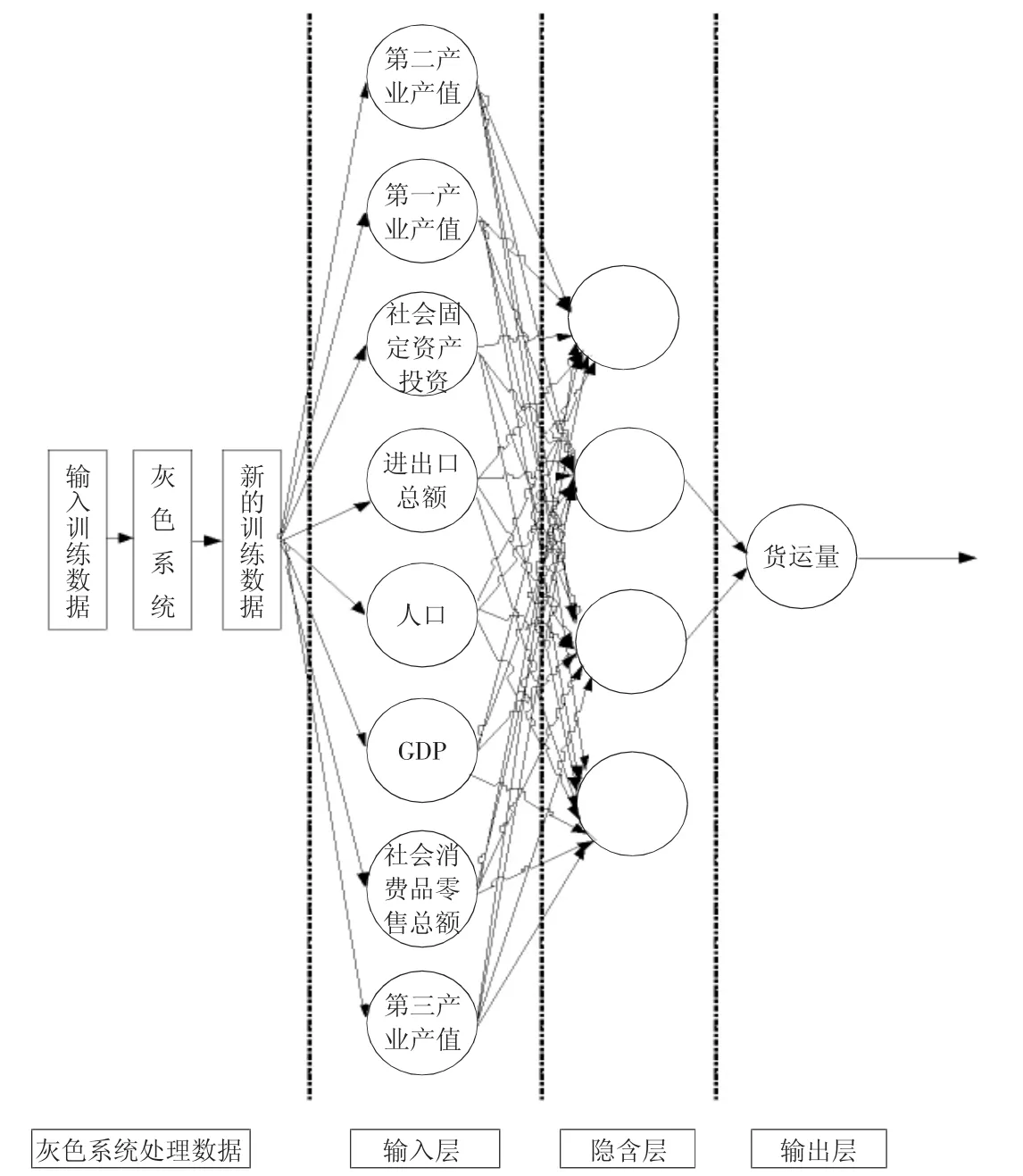
图1 云南省货运量灰色神经网络拓扑结构图
LA层到LB层调节后的权值为:

(5)根据预测的误差调节灰色神经网络的阈值
调节后的阈值为:
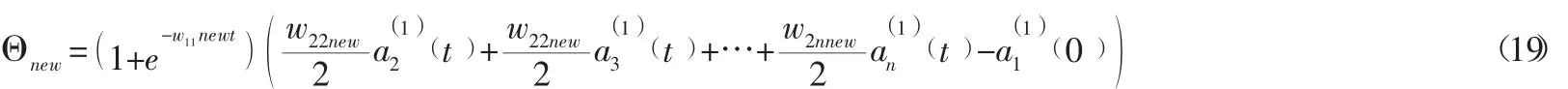
(6)判断灰色神经网络的训练是否达到期望误差的目标,若否,返回到第(2)步再次进行训练。
2 云南省货运量灰色神经网络预测模型
2.1 云南省货运量及其影响因素数据准备
货运量与多种因素密切相关,结合相关文献[8],本文选取的对货运量的主要影响因素有8个:人口、GDP、第一产业产值、第二产业产值、第三产业产值、社会消费品零售总额、社会固定资产投资、货物进出口总额。
将因变量(货运量) 定义为y,将8个自变量依次定义为(人口/万人)X1,(GDP/亿元)X2,(第一产业产值/亿元)X3,(第二产业产值/亿元)X4,(第三产业产值/亿元)X5,(社会消费品零售总额/亿元)X6,(社会固定资产投资/亿元)X7,(进出口总额/亿美元)X8。从《云南省统计年鉴》中得到2008~2018年的云南省货运量及其影响因素统计数据见表1。
2.2 云南省货运量灰色神经网络仿真实验分析
云南省货运量灰色神经网络预测步骤
(1)建立由人口、GDP、第一产业产值、第二产业产值、第三产业产值、社会消费品零售总额、社会固定资产投资、货物进出口总额这8个自变量和货运量这1个因变量组成的多维灰色模型GM (1,8)。
(2)对2008~2018年的云南省货运量及其影响因素样本数据进行归一化处理与累加处理,处理后的数据作为灰色神经网络的训练数据与测试数据。
(3)初始化灰色神经网络中的参数a=b1=b2=b3=b4=b5=b6=b7=b8=(0.3,0.5 )5之间的一个随机数。
(4)初始化灰色神经网络中的学习速率u1=u2=u3=u4=u5=u6=u7=u8=0.0015。
(5)初始化灰色神经网络中的权值与阈值。
(6)将2008~2012年的5组数据作为训练数据,2013~2018年的6组数据作为测试数据。
(7)把灰色神经网络中的循环迭代次数设置为200次,设置权值修正函数与阈值修正函数,将LA层到LB层的刺激函数设置为sigmoid函数,其他层之间的刺激函数设置为purelin线性函数。
(8)灰色神经网络利用2008年到2012年的5组训练数据进行自我学习与自我适应不断修改权值与阈值,直到达到最小误差目标或者最大学习次数,建立云南省货运量灰色神经网络模型。
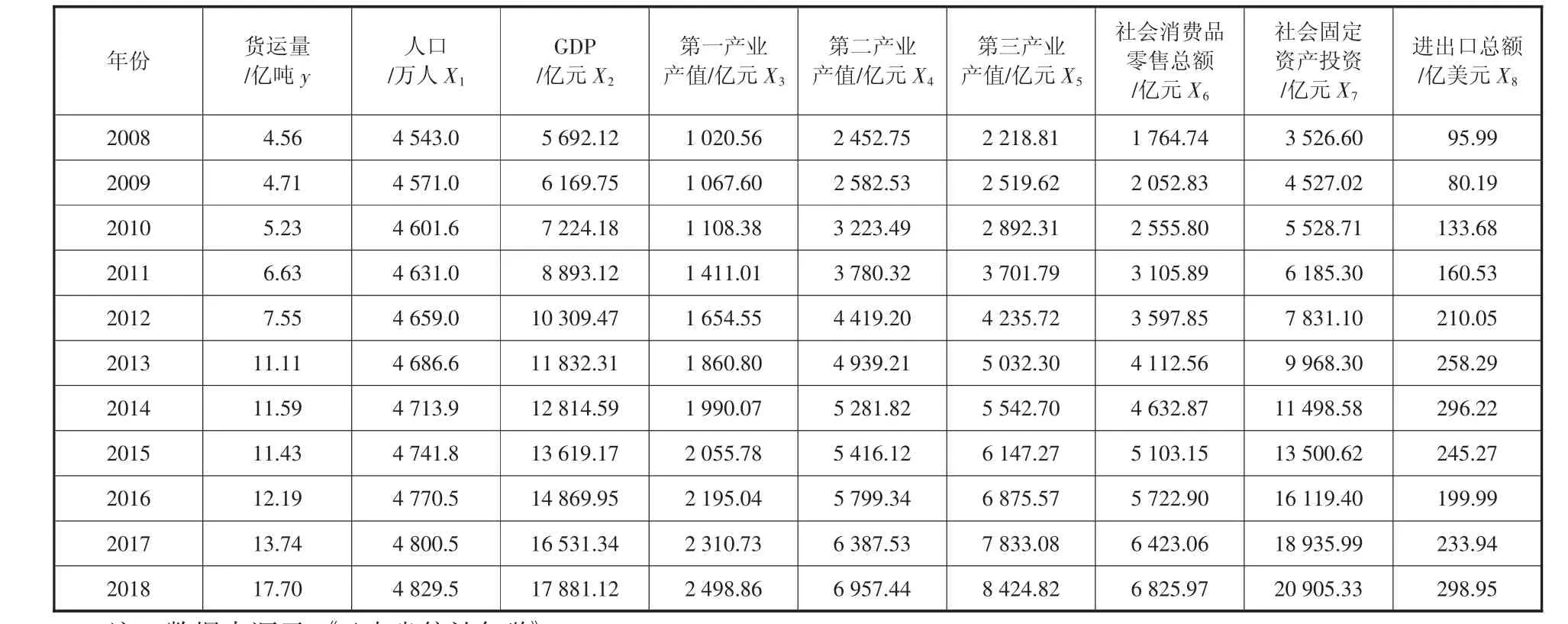
表1 2008~2018年云南省货运量及其影响因素
(9)用建立好的云南省货运量灰色神经网络模型对云南省2013~2018年的货运量进行预测,并将预测值与2013~2018年的6组测试数据进行对比。
使用matlab 2018a仿真软件按照云南省货运量灰色神经网络算法流程对灰色神经网络多维模型GM (1,8)进行编程,并运行程序,运行结果得到灰色神经网络的各个参数为:w11=5.6642,w21=-0.456,w22=0.0705,w23=0.4078,w24=0.6314,w25=0.4171,w26=-0.5033,w27=0.3567,w28=0.0470,w29=0.0461,w31=w32=w33=w34=w35=w36=w37=w38=w39=1.6828,a=0.3815,b1=0.4141,b2=0.4784,b3=0.5211,b4=0.480,b5=0.3046,b6=0.4686,b7=0.4096,b8=0.4094,LB_b=1,LC_c1=-0.456,LC_c2=0.3634,LC_c3=5.1318,LC_c4=1.2106,LC_c5=2.1370,LC_c6=-2.7893,LC_c7=1.6370,LC_c8=0.5574,LC_c9=1.0208,LD_d=14.8304,theta=4.1784。
由灰色神经网络模型公式:
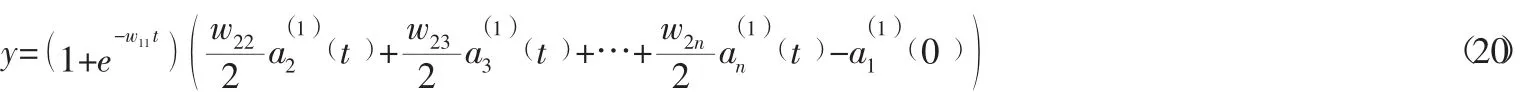
得到云南省货运量灰色神经网络的预测模型为:
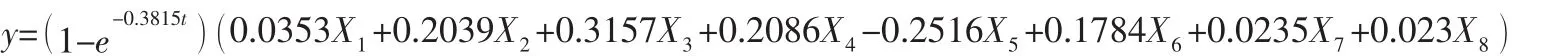
用云南省货运量灰色神经网络的预测模型与云南省货运量BP神经网络算法各自预测2013~2018年的云南省货运量,得到如图2所示的云南省货运量预测结果对比图。由图2可知灰色神经网络预测值与实际货运量的拟合效果最好。表2为灰色神经网络与BP神经网络预测结果对比。由表2可知灰色神经网络预测结果更好,灰色神经网络的最小相对误差为0.11%,最大相对误差为5.34%,平均相对误差为2.46%。而BP神经网络的最小相对误差为12.08%,最大相对误差为16.56%,平均相对误差为13.52%。灰色神经网络的预测结果误差要小得多。
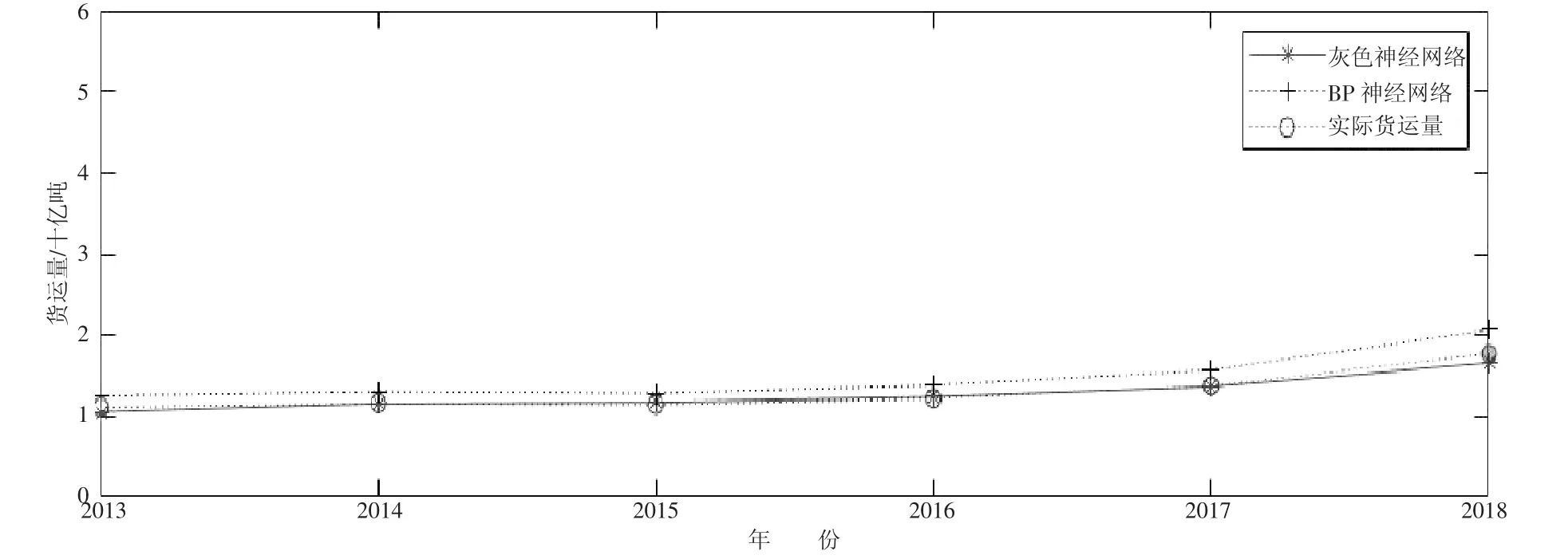
图2 云南省货运量预测结果对比图
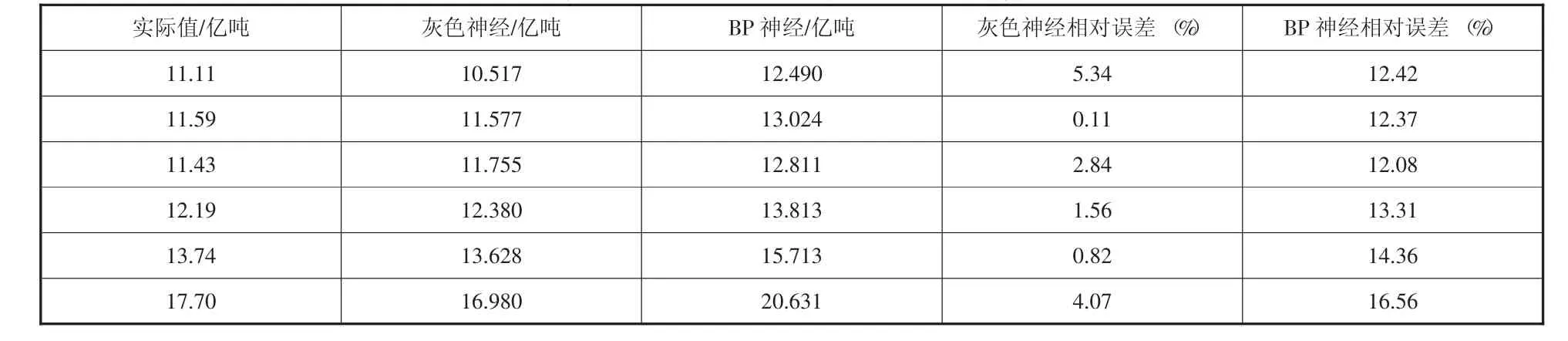
表2 灰色神经网络与BP神经网络预测精度对比
3 结 论
本文主要研究了灰色神经网络对云南省货运量的预测,并将灰色神经网络预测值与BP神经网络预测值进行了对比。预测结果表明,灰色神经网络预测结果比BP神经网络预测结果拥有更高的精度,能取得更好的预测结果。取得较高精度预测结果的主要原因是灰色神经网络结合了BP神经网络与灰色系统两者的优点。云南省可以根据灰色神经网络对货运量的预测,对相关资源进行优化配置与改革,促进云南省经济与社会的发展。
