基于M-C方法的复杂气井井筒完整性失效因素不确定性分析

刘铭刚，李 勇，王廷春，万古军，高凯歌，逄铭玉

(中国石化青岛安全工程研究院，山东青岛 266071)

0 引言

井筒完整性(Wellbore Integrity,简称WI)评价技术的研究始于1977年BP公司首先建立的油气井完整性管理体系，2010年“深水地平线事件”后，挪威石油工业协会牵头由BP、Conoco Phillips、Eni Norge、Exxon Mobil、Marathon、Nexen Inc.、Norske Shell、Statoil、Total等组成工作团队完成对Norsok D-010标准《Well Integrity in Drilling and Well Operations》(Revision 3, Aug.2004)的编制，2011年美国石油学会发布API 96《Deepwater Well Design and Construction》。

目前工程上进行井筒完整性分析时，存在贡献因素庞大导致的模型复杂化问题，这是因为由油管-套管-水泥环-地层复合结构形成的复杂气井井筒，离散度相比单一材料结构大得多，且该系统对注采气过程中的井筒完整性不确定性参数，如各结构的材料及尺寸、外部载荷、边界条件、工况设置等有很高的敏感性，这些参数的随机性为井筒完整性评价增加了难度。因此在进行可靠性分析或完整性分析时，必须对具有不确定性的结构或力学参数进行随机性分析。对井筒结构，涉及的不确定性参数主要有：管柱材料参数不确定性、管柱强度不确定性、水泥环材料参数不确定性、水泥环强度不确定性、井筒围岩参数不确定性、原始地应力不确定性等。本文分别基于不同的随机性指标进行不确定性分析，得到影响复杂气井井筒完整性参数的随机分布情况，并给出相应的概率密度。

1 基于M-C方法的失效贡献因素随机分析方法

Monte-Carlo方法(简称M-C方法)计算复杂气井井筒完整性失效概率的步骤如下。

a)通过统计或其他方法获取复杂气井井筒完整性失效的贡献因素Xi(i=1,2,3,…,n)，及每个贡献因素的概率分布。

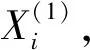
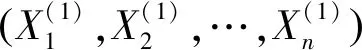
d)判断N个随机数Z(1),Z(2),…,Z(N)里面是否满足以下条件，即存在M(M≤N)个随机数Z(i)(1≤i≤M)，满足Z(i)<0，则在抽样次数足够多(N足够大)的情况下，根据大数定理[1]可知复杂气井井筒完整性的失效概率为

Pf=P(Z<0)=M/N

(1)

e)拟合Z的概率分布曲线，进而得到状态函数的平均值μZ和方差σZ，利用公式(2)、公式(3)、公式(4)即可求得复杂气井井筒完整性的可靠性指标β、失效概率Pf和可靠概率Ps

(2)

Pf=1-Φ(β)

(3)

Ps=Φ(β)

(4)

根据文献[2]可知，复杂井筒的各结构对“复杂气井井筒完整性失效”这一顶事件的贡献因素重要度排名为：油管等效应力、套管等效应力、水泥环切应力、第一胶结面切应力、第二胶结面切应力和地层切应力。可靠度计算时，仅需对上述6个最重要的贡献因素进行概率计算。假设上述6个贡献因素对应的失效事件互相独立，则根据Bayes定理[3]求得最终的井筒系统可靠概率为

(5)

式中：C——复杂气井井筒完整性良好的事件；

Ci——贡献因素；

Ps(C)——复杂气井井筒完整性良好的事件的发生概率；

Ps(Ci)——贡献因素的重要度大小；

Ps(C|Ci)——贡献因素Ci发生C事件的概率。

2 工程实例

2.1 管柱材料参数和强度随机性分析

算例井T1、T2和T4的油管柱材料均为N80钢，套管柱材料均为P110钢。对算例井所用上述管材按照国家标准[4-6]进行试件的加工和试验。试验所用N80钢、P110钢MTS试验装置和标准试件如图1所示，常温和高温下试验获得的N80钢、P110钢应力-应变曲线如图2所示，图中所示为一般试验工况。

图1 N80钢、P110钢标准试件

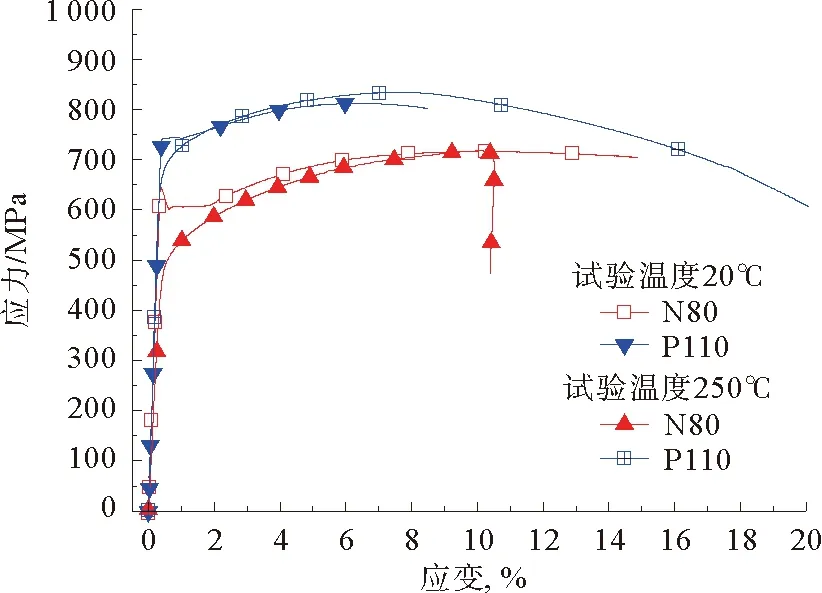
图2 N80钢、P110钢拉伸试验应力-应变曲线

根据大量管材试验结果及生产厂家统计数据，得到的油管柱(N80钢)的弹性模量和泊松比随机性分析结果直方图和概率密度曲线如图3和图4所示。套管柱(P110钢)的弹性模量和泊松比随机性分析结果直方图和概率密度曲线如图5和图6所示。可以看出，油管、套管材料参数的随机性满足Gaussian分布。

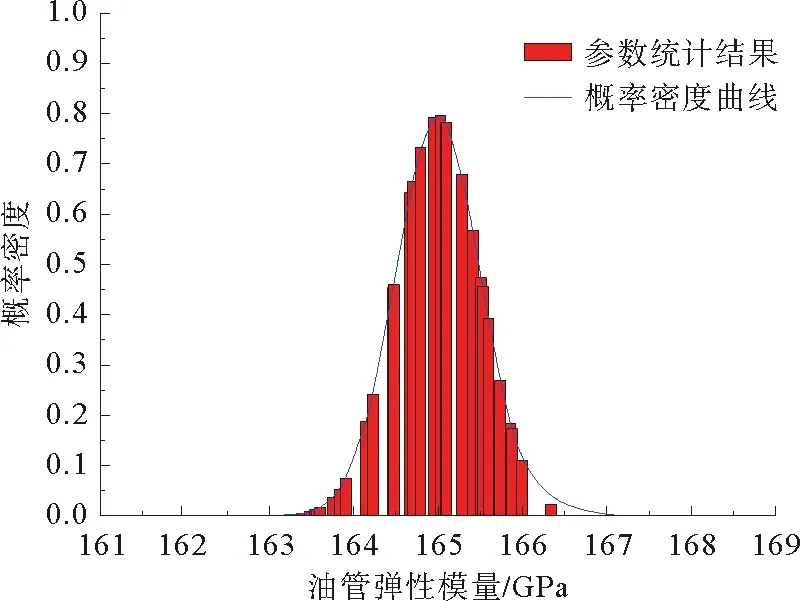
图3 油管材料弹性模量随机性分析结果

图4 油管材料泊松比随机性分析结果

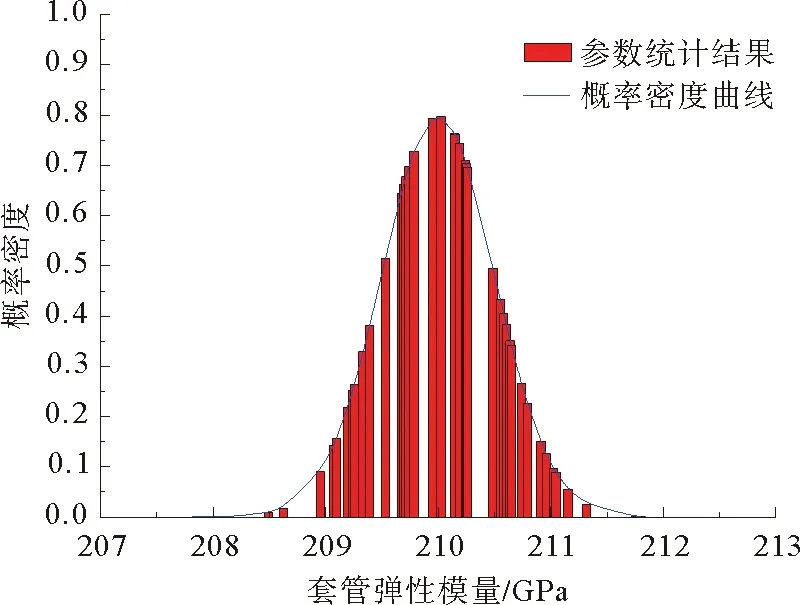
图5 套管材料弹性模量随机性分析结果

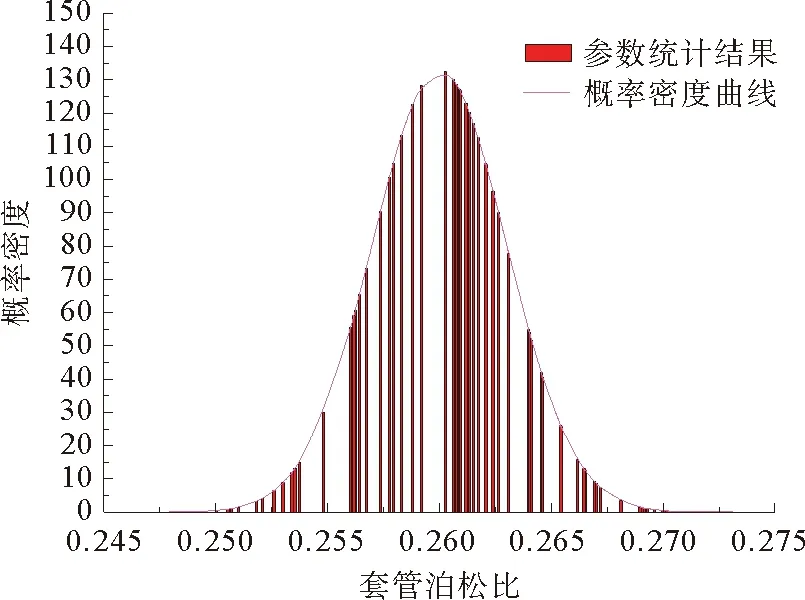
图6 套管材料泊松比随机性分析结果

材料试验得到的油套管抗拉强度和屈服强度的随机性分析结果如图7～图10所示。可以看出，油管、套管的强度参数随机性同样满足Gaussian分布。

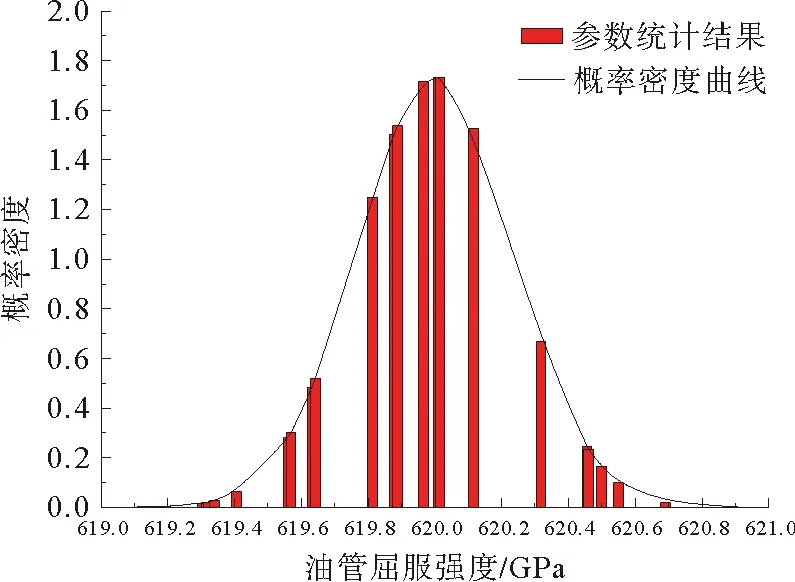
图7 油管屈服强度随机性分析结果

图8 油管抗拉强度随机性分析结果

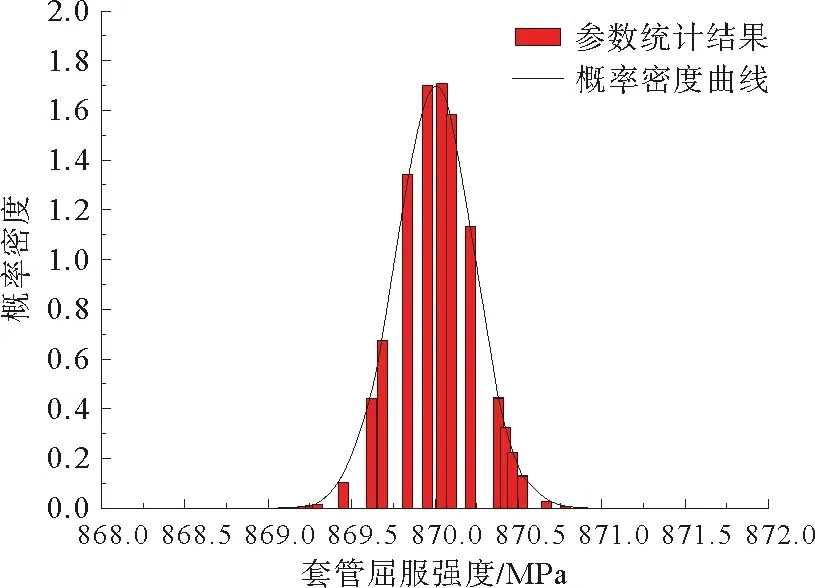
图9 套管屈服强度随机性分析结果

2.2 水泥环材料参数和强度随机性分析

基于现场反馈资料得到的水泥环弹性模量和泊松比随机性分析结果直方图和概率密度曲线如图11和图12所示。可以看出，水泥环材料参数随机性满足Gaussian分布。

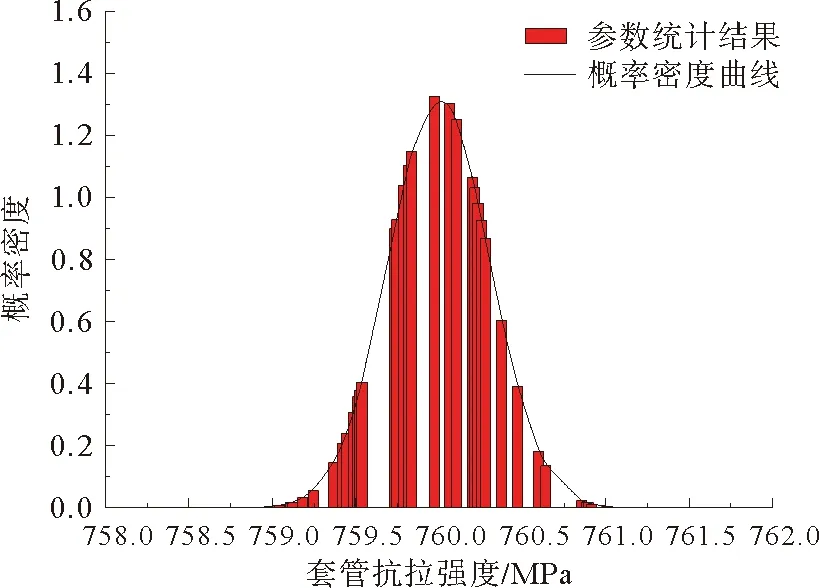
图10 套管抗拉强度随机性分析结果

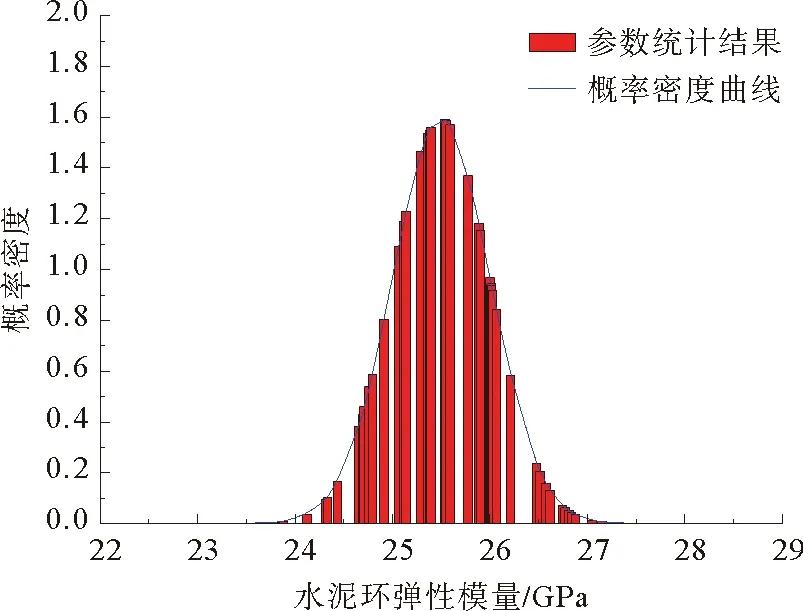
图11 水泥环弹性模量随机性分析结果

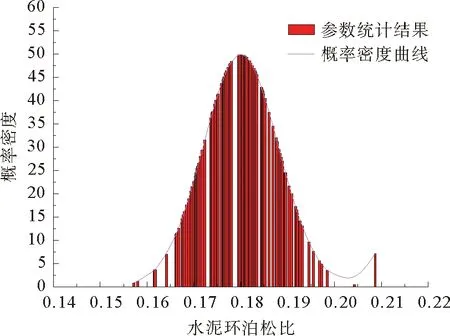
图12 水泥环泊松比随机性分析结果

基于巴西试验得到的水泥环抗剪强度随机性分析结果直方图和概率密度曲线如图13所示。可以看出，水泥环强度参数随机性同样满足Gaussian分布。

2.3 岩石材料参数和原始地应力随机性分析

根据测井资料解释和岩石参数处理方法[7-10]，得到算例井地层弹性模量和泊松比随机性分析结果如图14和图15所示。可以看出，地层岩石的材料参数随机性满足Gaussian分布。

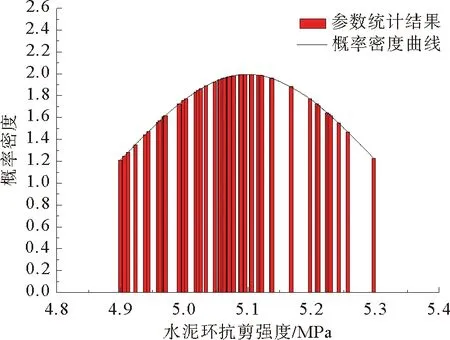
图13 水泥环抗剪强度随机性分析结果

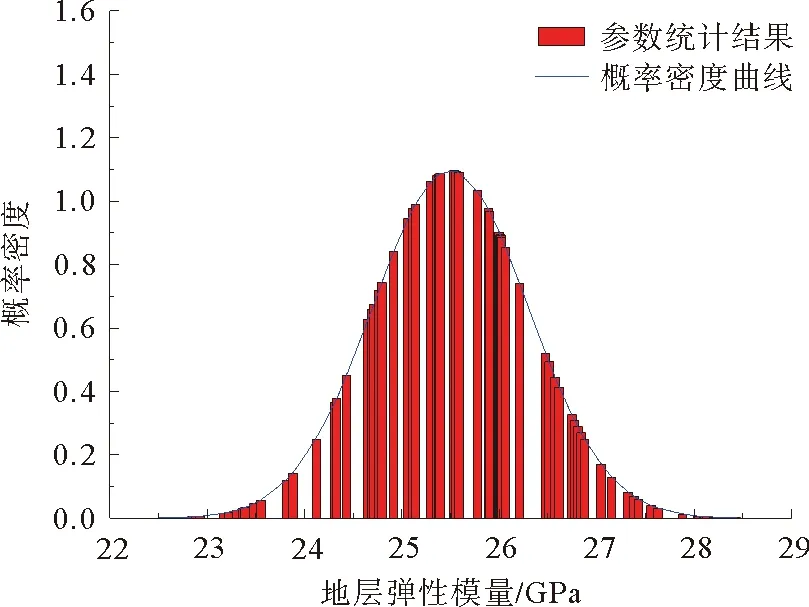
图14 地层弹性模量随机性分析结果

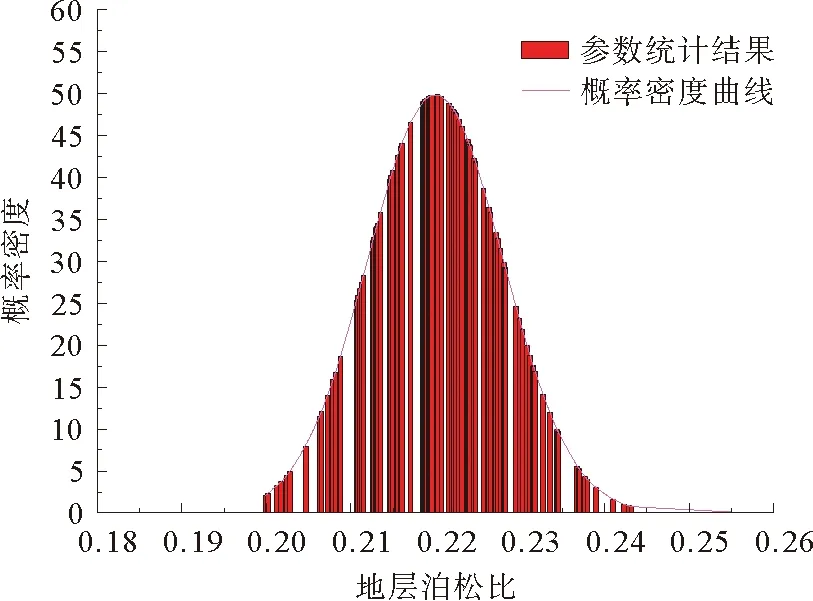
图15 地层泊松比随机性分析结果

基于巴西试验得到的岩石抗剪强度随机性分析结果直方图和概率密度曲线如图16所示。可以看出，岩石强度参数随机性同样满足Gaussian分布。

3 结论及建议

a)在工程和实验室样本下基于M-C方法得到的管柱材料参数、管柱强度、水泥环材料参数、水泥环强度和井筒围岩参数均符合Gaussian分布。

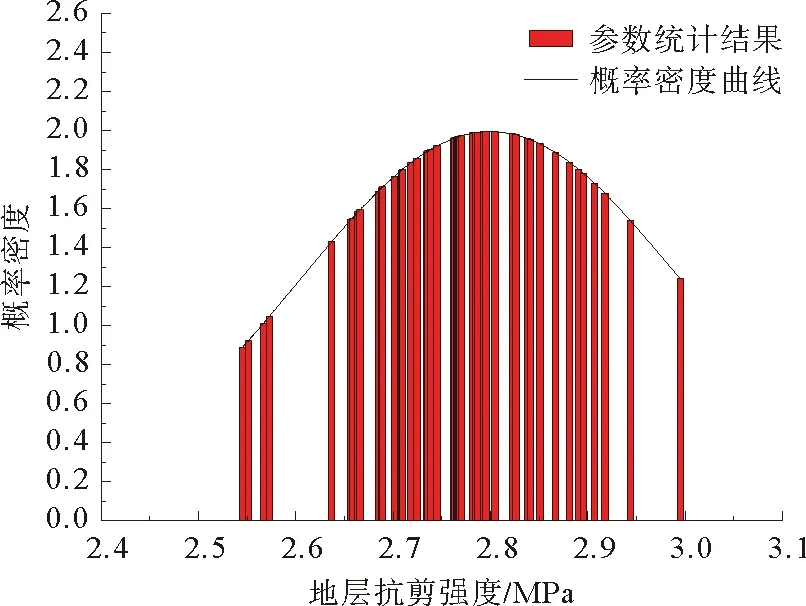
图16 地层抗剪强度随机性分析结果

b)基于M-C方法的复杂气井井筒完整性失效贡献参数的不确定性分析结果受样本空间影响很大，样本区间越大，结果精度越高。

c)后续开展复杂气井完整性失效贡献因素的不确定性分析时建议引入更多相关性参数，如时间、管柱材料的超低周疲劳和地层蠕变等，增加分析精度和结果的可信度。