聚合物驱牛顿—非牛顿—牛顿三区复合试井模型

刘文涛，张德富，程宏杰，王晓光

（中国石油新疆油田公司勘探开发研究院，新疆克拉玛依834000）

试井分析作为油气藏动态监测和地层参数求取的重要手段，国内外许多学者对存在非牛顿流体条件下的试井解释模型已经有了一定的研究。关于非牛顿幂律流体的研究，国外学者IKOKU和RAMEY[1-2]研究了多孔介质中非牛顿幂律流体不稳定渗流特征，建立并求得了考虑井储和表皮效应的试井解释数学模型拉氏空间解；我国学者栾志安[3]建立了双重介质非牛顿流体的试井解释模型并求得了拉氏空间解析解；对于复合油藏试井解释模型的研究，我国学者宋考平、刘彬、程时清、朱常玉、徐有杰等[4-11]对于不同的注采方式分别建立了非牛顿流体—牛顿流体双区复合、多区复合、牛顿流体—非牛顿双区流体复合以及非牛顿流体—牛顿流体—牛顿流体三区复合试井解释数学模型并求得了拉氏空间解析解。这些模型的建立为聚合物驱油试井资料的解释打下了很好的基础。

聚合物驱作为油气藏提高采收率的重要手段，随着三次采油技术的不断进步，在三次采油中发挥着极其重要的作用。注聚合物驱油时，通常采用前缘水驱—聚驱—后续水驱的注入方式。聚合物被视为非牛顿幂律流体，聚合物没有驱替到的区域被视为牛顿流体，从而形成了一个由牛顿流体—非牛顿流体—牛顿流体构成的三区复合油藏模型。

基于之前的研究，建立了由牛顿流体—非牛顿幂律流体—牛顿流体构成的三区复合油藏试井解释数学模型，通过拉普拉斯变换求出了模型在拉普拉斯空间的解析解，利用Stefest数值反演算法[12]做出无因次压力、无因次压力导数与无因次时间的双对数理论图版并进行了响应的影响因素分析。

1 数学模型的建立与求解

1.1 数学模型的建立

当以注入井为中心，进行前缘水驱—聚驱—后续水驱（图1）的注入方式时，根据IKOKU的研究，在聚合物溶液注入的区域，地层流体可视为非牛顿幂律流体，前缘水驱和后续水驱地层流体可视为牛顿流体，形成由牛顿流体—非牛顿流体—牛顿流体组成的三区复合油藏试井解释模型（图1）。其他假设条件如下：

1）油层为水平、均质、等厚的无限大地层，流动呈层流。

2）各区内流体均为单相微可压缩的液体，忽略重力和毛管力的影响。

3）各区内流体均符合达西平面径向渗流规律，等温渗流。

4）考虑井筒储存效应和表皮效应的影响。

5）两相邻渗流区域界面不存在附加压力降，不考虑相间的吸附效应。

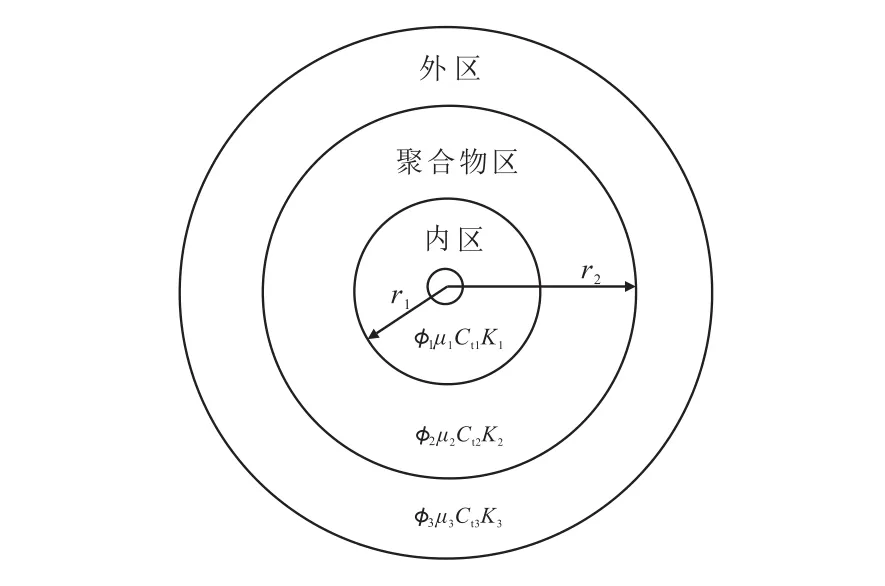
图1 三区复合油藏示意图Fig.1 Composite reservoir with three parts

6）非牛顿流体黏度服从Ostwald-De Waele[13]幂律流体模型。根据文献[13]可得：

基于上述假设条件，建立考虑井筒储存效应和表皮效应影响的牛顿流体—非牛顿幂律流体—牛顿流体三区复合油藏试井解释数学模型如下：

无限大外边界：

式中：

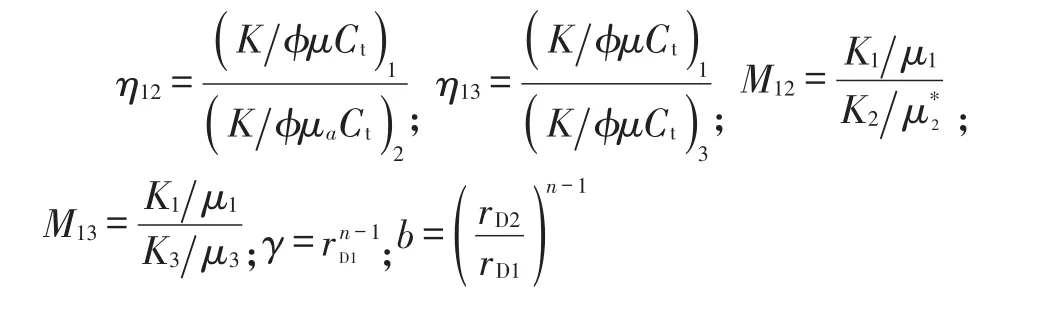
无因次变量定义：

1.2 试井数学模型求解

对式（2）进行拉普拉斯变换得到3个区域微分方程的通解分别为：

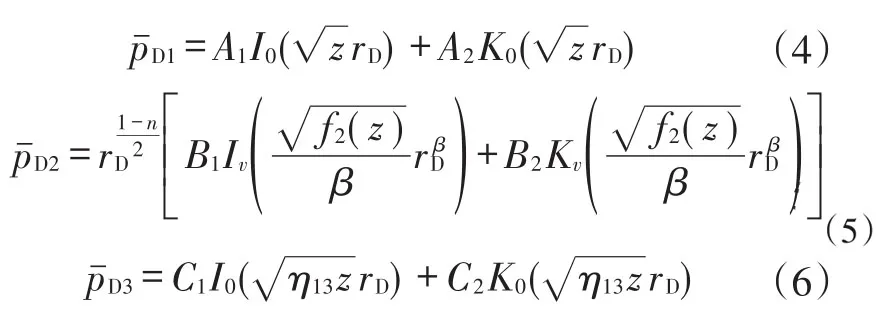
式中：

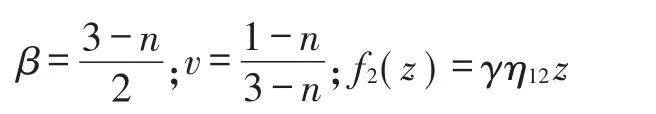
对于无限大边界，根据贝塞尔函数的相关性质得：C1=0。

分别将式（4）—（6）代入式（2）的边界条件求得无因次井底压力为：

式中：

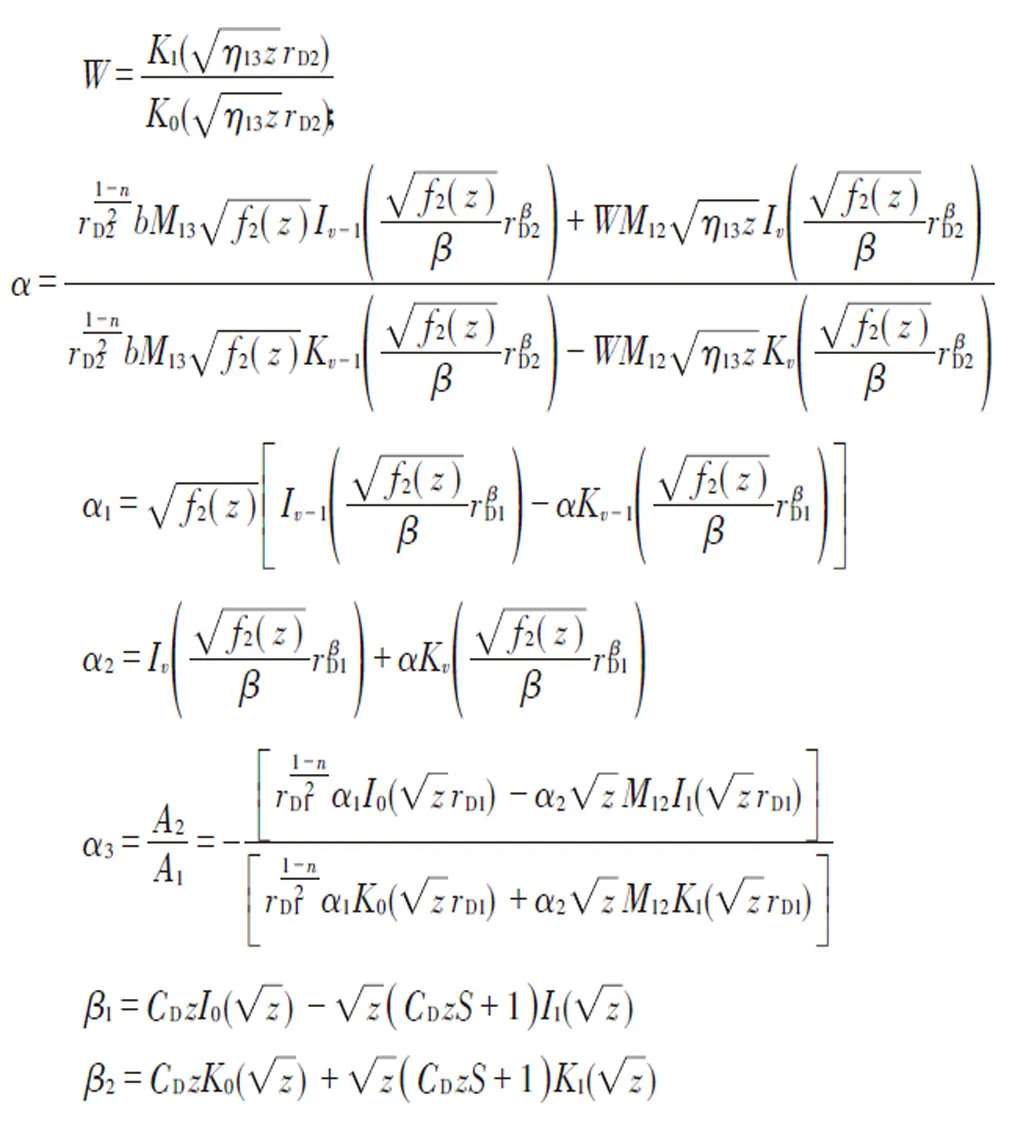
2 典型曲线特征及影响因素分析

利用Stehfest数值反演算法对式（7）进行反演，可得到无限大外边界条件下无因次压力与压力导数关于无因次时间的典型曲线。

图2是聚合物驱牛顿—非牛顿—牛顿三区复合油藏试井模型典型曲线。根据导数曲线特征，可划分为7个阶段：第一阶段为井筒储集效应阶段，无因次压力及导数曲线重合，呈一条斜率为1的直线；第三阶段为内区径向流阶段，描述内区牛顿流体的渗流特征，导数曲线呈值为0.5的水平直线；第五阶段为聚合物区径向流阶段，描述聚合物区非牛顿幂律流体的渗流特征，导数曲线呈现（1-n）/（3-n）斜率的直线，幂律指数越小，曲线越陡；第七阶段为外区径向流阶段，导数曲线呈一条水平直线，水平直线的值为M13/2；第二、四、六阶段为过渡段。

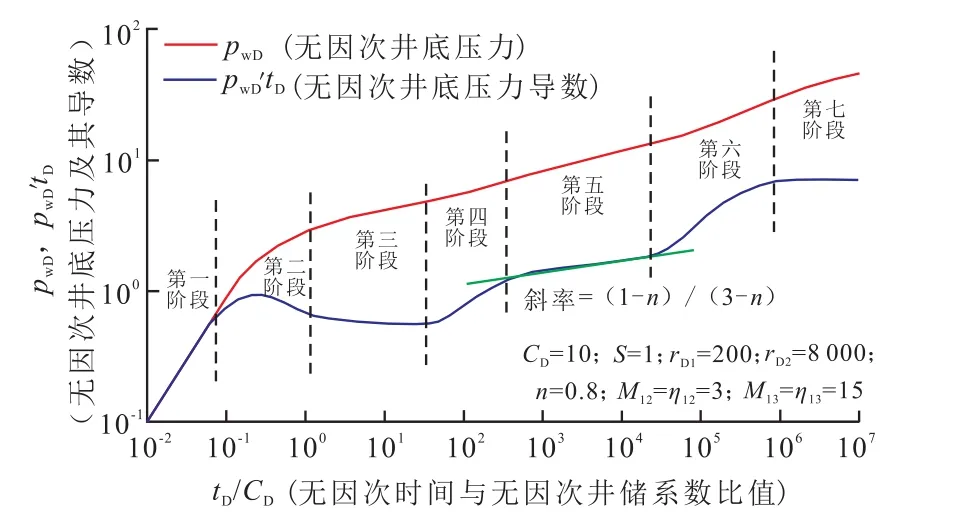
图2 聚合物驱牛顿—非牛顿—牛顿三区复合油藏试井模型典型曲线Fig.2 Typical curves of well test model of three parts composite reservoirs with Newtonian/non-Newtonian/Newtonian for polymer flooding

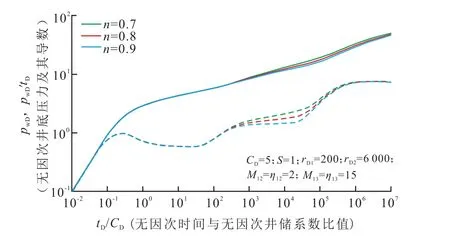
图3 幂律指数对井底压力动态的影响关系曲线Fig.3 Relation curves of influence of power-law index on dynamic of bottom-hole pressure

图3为幂律指数n对井底压力动态的影响关系曲线。由于聚合物区为聚合物溶液，幂律指数的变化主要影响聚合物区径向流阶段的压力导数曲线特征，幂律指数n越小，聚合物区径向流阶段压力导数曲线越陡。也就是说，幂律指数n越小，流体流动越困难，压力波在聚合物区的传播越慢；如果幂律指数n为0，则流体不流动，相当于存在封闭外边界的情形，导数曲线呈斜率为1的上翘直线，表现为封闭边界的特征。

图4为内区半径rD1对井底压力动态的影响关系曲线。内区半径的变化主要影响流体在内区和聚合物区地层内流动的持续时间。内区半径rD1越小，相对来说聚合物区范围则越大；压力波在内区流动持续的时间越短，在聚合物区流动持续的时间越长。在无因次压力导数曲线上主要表现为内区径向流阶段结束时间越早，导数曲线0.5水平线越短；聚合物区径向流开始时间越早，导数曲线呈（1-n）/（3-n）斜率的直线段则越长。

图4 内区半径对井底压力动态的影响关系曲线Fig.4 Relation curves of influence of radius of inner part on dynamic of bottom-hole pressure

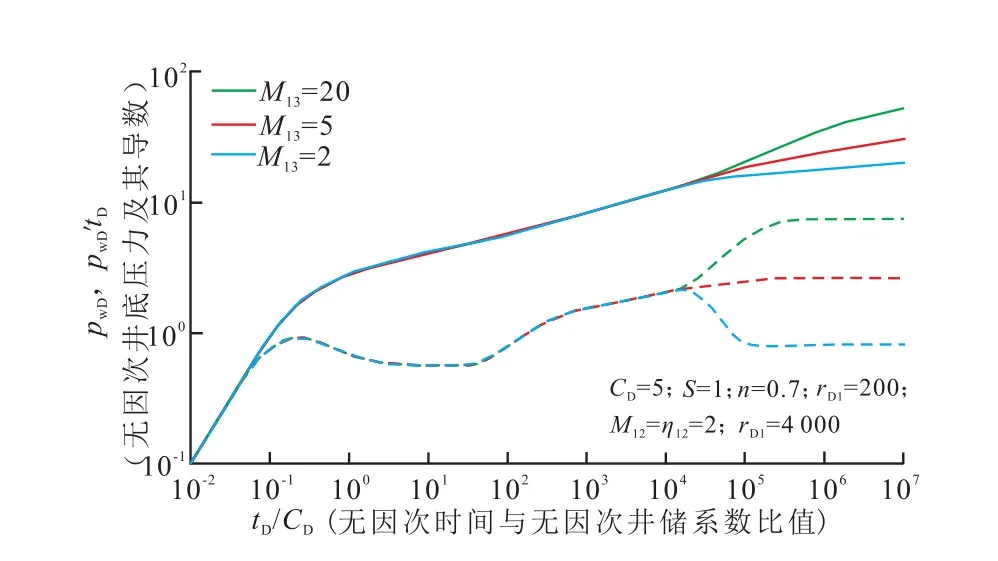
图6 内区与外区流度比对井底压力动态的影响关系曲线Fig.6 Relation curves of influence of mobility ratio of inner and outer part on dynamic of bottom-hole pressure

图5 聚合物区半径rD2对井底压力动态的影响关系曲线Fig.5 Relation curves of influence of radius（rD2）of polymer part on dynamic of bottom-hole pressure

图7 内区与聚合物区界面流度比对井底压力动态影响关系曲线Fig.7 Relation curves of influence of mobility ratio of inner part and polymer part on dynamic of bottom-hole pressure

图5为聚合物区半径rD2对井底压力动态的影响关系曲线。聚合物区半径的变化主要影响流体在聚合物区和外区地层内流动的持续时间。聚合物区半径rD2越大，压力波在聚合物区流动的范围越大、流动持续的时间越长。在无因次压力导数曲线上主要表现为聚合物区径向流阶段结束时间越晚，导数曲线呈（1-n）/（3-n）斜率的直线段越长；外区径向流阶段开始时间越晚。

图6为内区与外区流度比M13对井底压力动态的影响关系曲线。由于内区和外区都是牛顿流体，所以内区与外区流度比的变化主要影响外区径向流阶段压力导数曲线位置的高低。内区与外区流度比M13越大，外区流体的流动能力越差，外区径向流阶段无因次压力导数曲线水平段位置越高，其值为M13/2；反之亦然。

图7为内区与聚合物区界面流度比M12对井底压力动态的影响关系曲线。由于内区是牛顿流体而聚合物区是非牛顿流体，所以在幂律流体的幂律指数一定的情况下，内区与聚合物区界面流度比的变化主要影响聚合物区径向流阶段压力导数曲线位置的高低，而不影响外区压力导数曲线位置的变化。内区与聚合物区界面流度比M12越大，聚合物区径向流阶段压力导数曲线位置越高，反之亦然。

3 结论

1）建立并求解了适用于聚合物驱油藏的牛顿流体—非牛顿流体—牛顿流体三区复合油藏试井解释模型，根据导数曲线特征可识别出四个典型的流动阶段：纯井筒储集效应阶段、内区牛顿流体径向流阶段、聚合物区幂律流体径向流阶段、外区牛顿流体径向流阶段。

2）在聚合物区幂律流体径向流阶段，压力导数双对数曲线呈（1-n）/（3-n）斜率的直线，幂律指数越小，导数曲线斜率越大。在外区牛顿流体径向流阶段，压力导数双对数曲线呈值为0.5M13的水平直线，M13越大，导数曲线位置越高。

3）内区和聚合物区半径主要影响其径向流阶段持续的时间：内区半径越小，内区径向流阶段结束时间越早，导数曲线0.5水平线越短；聚合物区半径越大，聚合物区径向流阶段结束时间越晚，导数曲线呈（1-n）/（3-n）斜率的直线段越长。

符号说明

B为地层原油体积系数，m3/（标）m3；C为井储系数，m3/MPa；Q为地面储量，m3/d；h为储层厚度，m；S为表皮系数，无因次；t为生产时间，h；rw为井筒半径，m；r为储层某处到井筒中心线的距离，m；ri为内区、聚合物区半径，m，（i=1，2）；n为幂律指数，无因次；pe为原始地层压力，MPa；pw为井底压力，MPa；Ki为内区、聚合物区和外区渗透率，μm2；Cti为内区、聚合物区和外区压缩系数，MPa-1；Pi为内区、聚合物区和外区压力，MPa-1；ϕi为内区、聚合物区和外区压力，无因次；μi为内区、聚合物区和外区流体黏度，mPa·s；μ*为幂律流体表观黏度，mPa·s；rwD为无因次井筒半径；CD为无因次井储系数；tD为无因次时间；pwD为无因次井底压力；piD为内区、聚合物区和外区无因次压力，（i=1，2，3）；riD为内区、聚合物区无因次半径，（i=1，2）；Kv（x），Iv（x）分别为v阶的第二类和第一类修正贝塞尔函数；I（0x），I（1x）分别为零阶和一阶的第一类修正贝塞尔函数；K0（x）、K（1x）分别为零阶和一阶的第二类修正贝塞尔函数；下标D表示无因次为进行拉普拉斯变换后的无因次井底压力为进行拉普拉斯变换后的无因次压力，当r=rw时，；PD为无因次压力，当r=rw时，PD=PwD；A为公式推导时的中间变量。