基于真实信息传播者的谣言传播模型的动力学分析*
2019-09-04张菊平郭昊明荆文君靳祯
张菊平 郭昊明 荆文君 靳祯†
1)(山西大学复杂系统研究所,太原 030006)
2)(山西大学,疾病防控的数学技术与大数据分析山西省重点实验室,太原 030006)
1 引 言
谣言,指的是没有相应事实基础,却被捏造出来并通过一定手段推动传播的言论.近年来,随着移动互联网+时代的到来,使信息化传播门槛进一步降低,加之移动通信工具的普遍,谣言传播变得速度更快,作用力更强.网络谣言滋生蔓延,不仅败坏个人名誉,给受害人造成极大的精神困扰,更损害国家形象,影响社会稳定.因此,对于谣言传播规律的研究十分必要.谣言传播模型的研究始于20世纪60年代,Daley和Kendall[1]提出的DK模型,按照谣言传播把受众分为三类,未曾听过谣言的人、传播谣言的人和听过谣言但不传播谣言的人,利用随机过程的方法进行分析.Sudbury[2]认为可以借鉴传染病SIR(susceptible-infectiveremoved)模型研究谣言的传播.Zanette[3,4]和Nekovee等[5]分别在小世界网络和无标度网络上研究谣言的传播.Moreno等[6]基于SIR模型在非均匀网络上建立网络谣言传播模型.Zhao等[7,8]研究提出了遗忘机制、记忆机制对谣言传播的影响.Deng和Li[9]在研究谣言传播模型时考虑了遗忘率和记忆率.Zan等[10]基于SIR模型提出了具有反击机制的谣言传播模型.Wang等[11]基于SIR模型提出了带有信任机制的谣言传播模型.Yang等[12]和He等[13]研究了真理传播和辟谣策略对于谣言传播的影响.Huo等[14]考虑了传播节点的活跃度,将谣言传播者分为高活跃状态下的传播者和低活跃状态下的传播者,最后得出谣言传播者的活跃程度对于谣言传播有着非常大的影响.Zhang和Zhu[15]建立了 I2S2R(ignorants-spreaders-stifler)的谣言传播动态模型.Xiao等[16]提出了一种基于进化博弈和反谣言信息的谣言传播动力学模型,证明谣言不仅受到反谣言信息的影响,而且还受到用户行为和心理因素的影响.顾亦然和夏玲玲[17]基于在线社交网络建立SEIR(susceptible-exposedinfective-removed)谣言传播模型,并提出重要熟人免疫策略.王辉等[18]研究了社会加强效应对谣言传播的影响.张亚明等[19]研究了双重社会强化对谣言传播的影响.万贻平等[20]在谣言传播模型的基础上增加谣言清除者,研究了谣言清除过程的网络谣言传播与抑制.冉茂洁等[21]同时考虑个体兴趣度差异和辟谣机制问题,提出建立了IWSR(ignorant-weak spreader-strong spreader-removal)谣言传播模型.赵敏等[22]考虑媒体正面宣传报道和负面报道对谣言传播的影响,基于社交网络建立了新的谣言传播模型.
在谣言传播过程中,一些人已知事实真相或经过判断知道真相,并传播有关谣言的真实信息,但是已有的研究未考虑真实信息传播对于谣言传播的动力学影响.因此加入真实信息的传播者会使得谣言传播更加符合实际,而且现有的谣言模型对其进行数学分析的较少.本文考虑真实信息传播的影响,建立谣言传播模型并对其进行动力学分析,第2节根据谣言传播的机理建立了含有真实信息传播者的谣言传播SITR模型;第3节给出了谣言传播的阈值条件;第4节讨论了谣言传播者存在真实信息传播者不存在平衡点的条件,及谣言传播者不存在真实信息传播者存在平衡点的条件,并分析了它们的动力学性态;第5节分析了谣言传播者与真实信息传播者共同存在的平衡点存在性及其动力学性态;第6节数值模拟验证理论结果;第7节为总结.
2 模型的建立
在谣言传播过程中加入真实信息的传播者,将人群分为四类:未知者 S(susceptible),谣言的传播者 I(infective),真实信息的传播者 T(true),免疫者R(removed).未知者与谣言传播者接触率为β,接触后未知者以概率α1成为谣言传播者,以概率 1−α1成为免疫者;未知者和谣言传播者与真实信息传播者接触,未知者和谣言传播者以概率δ成为真实信息传播者;谣言传播者与谣言传播者接触后,谣言传播者对谣言失去兴趣变为免疫者的概率为ϵ;谣言传播者的遗忘率为θ.
用S(t),I(t),T(t)和R(t)分别表示在t时刻的未知者、谣言的传播者、真实信息的传播者和免疫者的数量,N(t)表示在t时刻四类人群的总数,则有N(t)=I(t)+S(t)+T(t)+R(t).假设个体以恒定速率A进入人群且全部为未知者,四类人群以速率µ移出群体,他们之间的关系如图1所示.

图1 真实信息影响下谣言传播流程图Fig.1.Flow chart of rumor propagation under the influence of true information.
根据图1,建立SITR谣言传播模型如下:

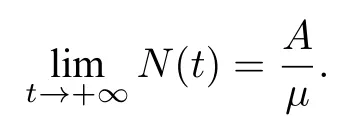
因为系统(1)的前三个方程不含R,因此只考虑系统(1)的前三个方程,得
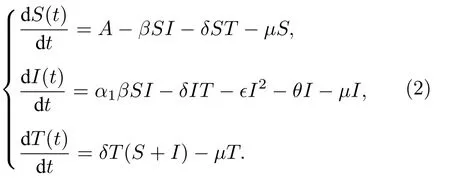
容易验证系统(2)的正向不变集是
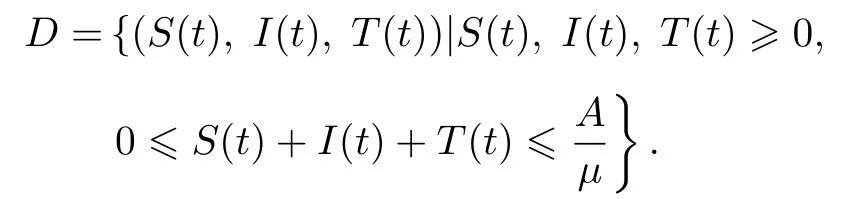
3 无谣言传播者无真实信息传播者平衡点与阈值
系统(2)有一个无谣言传播者无真实信息传播者平衡点E0(A/µ,0,0),下面用下一代矩阵法[23]求系统(2)的阈值.
记X=(I,T)⊤,⊤表示向量(I,T)的转置,则
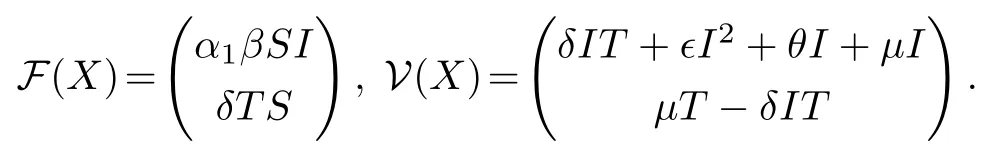
在无谣言传播者无真实信息传播者平衡点E0处有
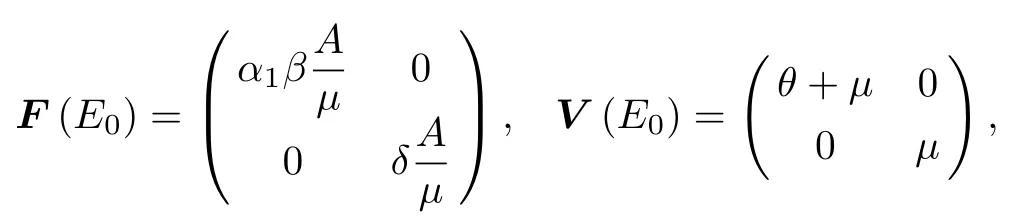
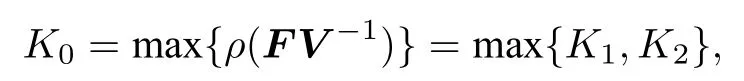
定理 1当K0<1 时,系统(2)的无谣言传播者无真实信息传播者平衡点E0是局部渐近稳定的.
4 边界平衡点的存在性及局部渐近稳定性
4.1 无谣言传播者但真实信息传播者存在的平衡点
在谣言传播的过程中,由于真实信息传播者的存在,人群中最终没有了谣言传播者,即无谣言传播者但有真实信息传播者平衡点存在性的问题.通过对系统(2)求平衡点得,如果K1>1,那么系统(2)存在无谣言传播者但有真实信息传播者平衡点简称为系统(2)的边界平衡点E1.
证明系统(2)在E1处的雅可比矩阵为


当K1>1 时,方程(3)的两个根都具有负实部.又当时,因此,当且时,是局部渐近稳定的.
4.2 谣言传播者存在但无真实信息传播者的平衡点
在谣言传播的过程中,可能会出现谣言传播者存在但没有真实信息传播者,即I=0,T=0.令系统(2)右端为零,当I=0,T=0 时,得到方程
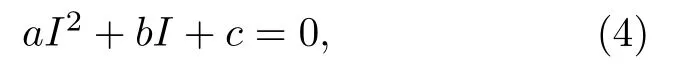
其中a=ϵβ>0,b=ϵµ+β(θ+µ)>0,c=µ(θ+µ)×(1−K2).
当K2<1 时,方程(4)无正实根.当K2>1 时,方程(4)存在唯一正根其中,∆=[ϵµ+β(θ+µ)]2−4ϵβµ(θ+µ)(1−K2).故当K2>1 时,系统(2)存在有谣言传播者但无真实信息传播者的平衡点我们称为边界平衡点E.2
定理 3当K2>1,且时,系统(2)的边界平衡点E2是局部渐近稳定的.
证明系统(2)在E2处的雅可比矩阵为
由2位具有多年影像诊断经验的核医学医师对所有患者的影像学资料进行背对背阅片,对受试者病灶感兴趣区(region of interest,ROI)进行勾画,并计算其最大标准摄取值(maximum standard uptake value,SUVmax)。18F-FDG PET/CT阳性的诊断标准为18F-FDG摄取的SUVmax高于周围本底水平(一般SUVmax≥2.5)或病灶同机平扫CT具有典型恶性形态学征象。
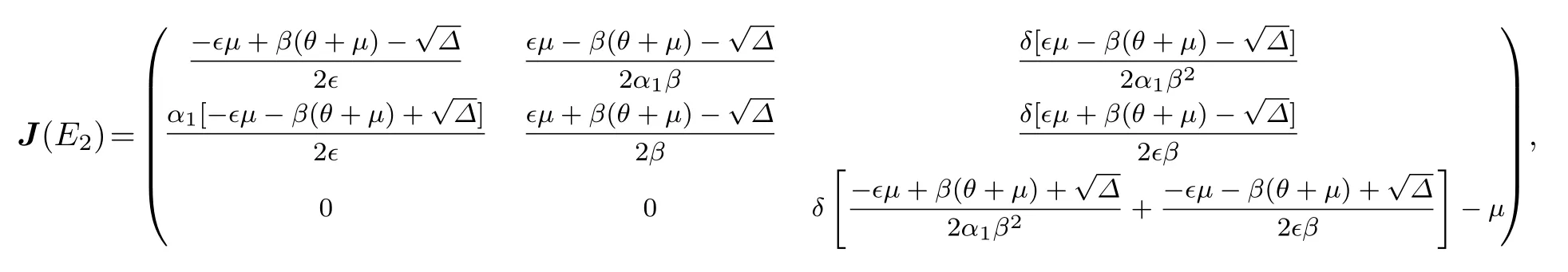
相应的特征方程为

其中,

q0=特征方程有一个特征根为

另外两个特征根满足方程
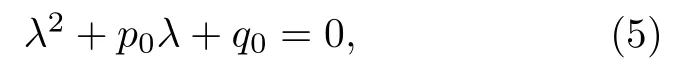

时,即

系统(2)的边界平衡点E2是局部渐近稳定的.令直线的斜率为
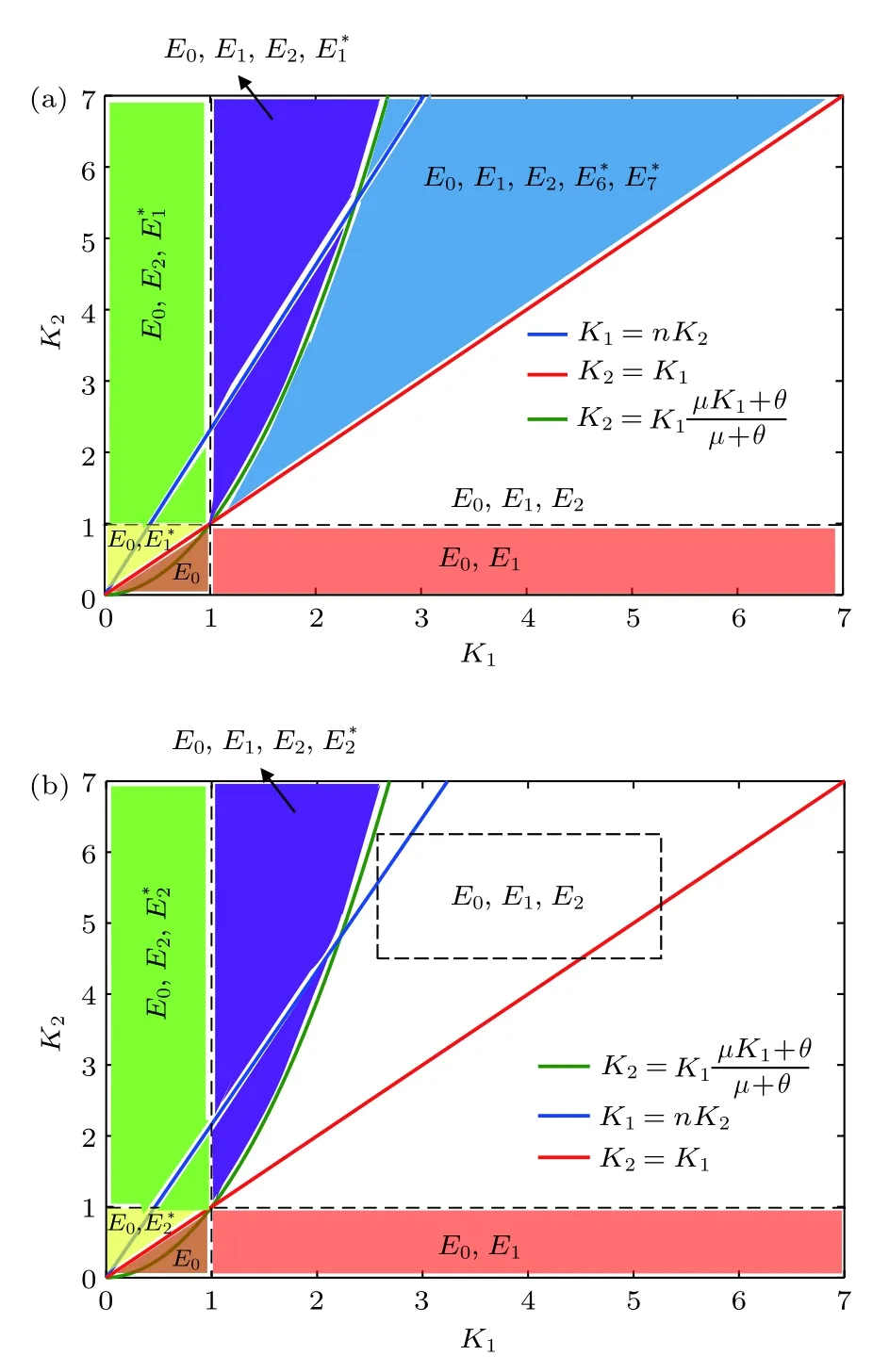
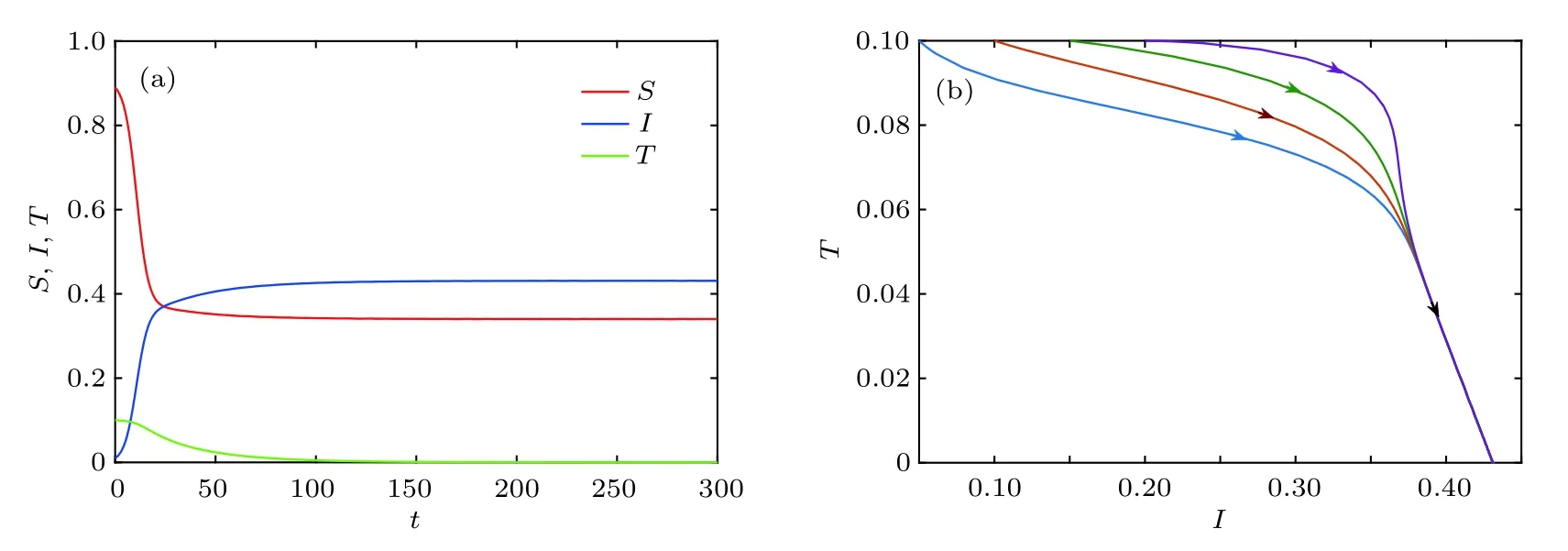
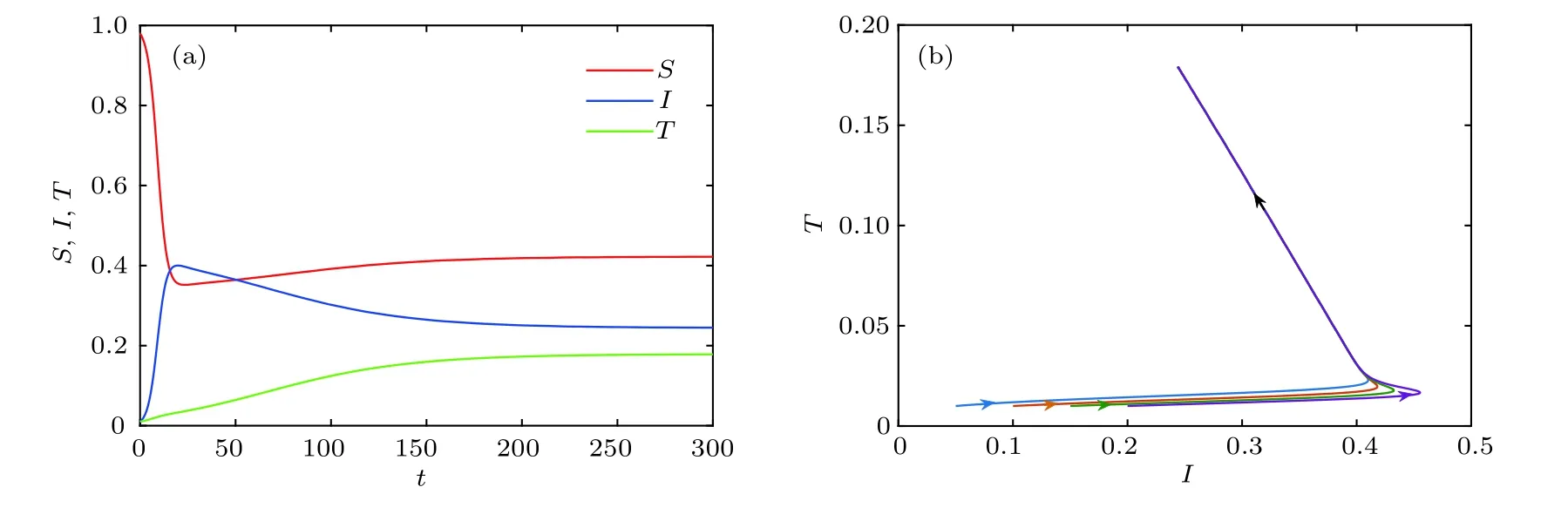
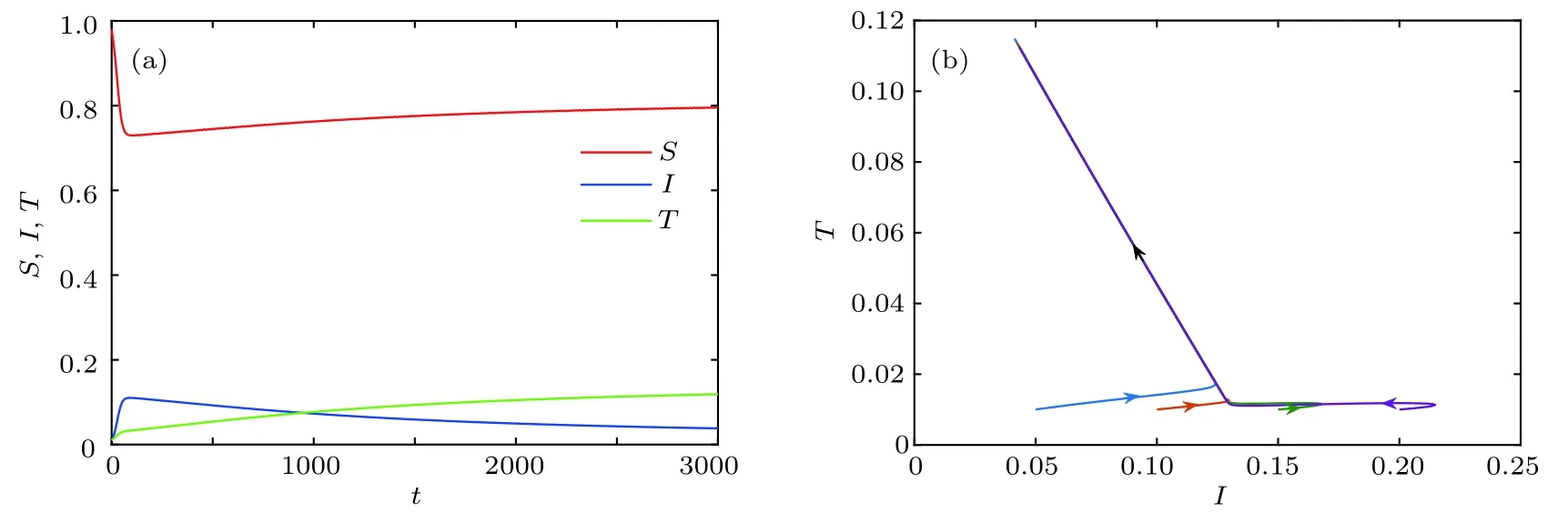
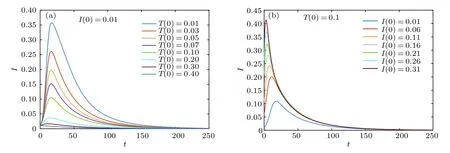
综上所述,当K1>1,且时,系统(2)存在边界平衡点E1,且E1是局部渐近稳定的(见图2).当K2>1,且K1 图2 K 1 与 K 2的关系图,参数取值为 α1=0.6,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01Fig.2.Diagram of K 1 and K 2.The parameter values are α1=0.6,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01. 下面求在谣言传播中,谣言传播者和真实信息传播者共存的平衡点,为了简便起见称其为正平衡点. 令系统(2)右端为零,当I=0,T=0 时,解得 其中,I∗满足方程 a0=方程(6)的判别式为 若正平衡点E∗(S∗,I∗,T∗)存在,则要求S∗>0,I∗>0,T∗>0.可得到0 下面分情况讨论方程(6)正根的存在性. 情形 1当时,有c0<0,所以 情形 2当时,有c0=0,∆1=b02>0. (i)当a0>0,b0<0,即时,方程(6)有唯一正实根因此,系统(2)存在唯一正平衡点 (ii)当a0<0,即ϵ>(1− α1)β时,有b0>0,此时方程(6)有唯一正实根 情形 3当时,有c0>0. (ii)当a0<0,即ϵ>(1− α1)β时,有b0>0,∆1>0.此时方程(6)有唯一正实根I8∗=(舍去).因此,系统(2)的正平衡点存在性仅在K2>K1范围内考虑. 综上所述,系统(2)平衡点的存在性分下面两种情形: 图3 K 1 与 K 2 关系图(α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01)(a)ϵ=0.01,ϵ <(1− α1)β ;(b)ϵ=0.3,ϵ>(1−α1)βFig.3.Diagram of K 1 and K 2(α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01 ):(a)ϵ=0.01,ϵ <(1− α1)β ;(b)ϵ=0.3,ϵ>(1−α1)β. 2)ϵ>(1− α1)β:具体见图3(b). 因此,我们进一步表示系统(2)平衡点之间的关系见表1. 定理4当且ϵ<(1−α1)β时,如果 那么系统(2)的正平衡点E1∗是局部渐近稳定的. 证明系统(2)在正平衡点E∗(S∗,I∗,T∗)处的雅可比矩阵为 相应的特征方程为 表1 系统(2)平衡点之间的关系Table 1. Relationship table between the equilibria of system(2). 和 把I1∗代入得从而知W3与W2同号.进一步把I1∗代入W2,由 Hurwitz 判据[24]可知,当W2>0,即 时,E1∗是局部渐近稳定的. 注:1)可类似证明其他正平衡点的稳定性. 2)当ϵ=0 时,阈值K0,无谣言传播者无真实信息传播者平衡点E0,及无谣言传播者但真实信息传播者存在的平衡点E1没有变化;谣言传播者存在但无真实信息传播者的平衡点E2的大小发生变化,影响着双稳区域;谣言传播者真实信息传播者共存的平衡点(即正平衡点)存在的条件及个数发生变化,影响着其动力学性态. 为了验证理论结果,下面对系统(2)进行数值模拟. 参数取值为α1=0.3,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.15时,K1=0.75<1,K2=0.857<1,则E0渐近稳定(见图4). 参数取值为α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01.当取δ=0.36时,K1=则E1渐近稳定(见图5).当取δ=0.22时,K2=3>1,K1=1.1 从图5可以看出,随着谣言的传播,谣言传播者的数量会达到一个峰值,之后不断下降,真实信息传播者数量随着时间逐渐增大,最后达到稳定状态.即系统(2)达到没有谣言传播者,只有真实信息传播者和易感者的稳定状态.从图6可以看出,随着谣言的传播,谣言传播者的数量逐渐增加,真实信息传播者数量会逐渐减少变为零,最后达到稳定状态.即系统(2)达到没有真实信息传播者,只有谣言传播者和易感者的稳定状态. 参数取值为α=0.4,β=0.7,A=0.2,µ=0.2,ϵ=0.01,θ=0.01,δ=0.234,且满足值不相同时,系统(2)的解会趋于不同的边界平衡点(见图7). 参数取值为α1=0.7,β=0.9,δ=0.3,A=0.2,µ=0.2,θ=0.01,则2.21429.当取ϵ=0.01时,ϵ=0.01<(1−α1)β=是渐近稳定的(见图8).当取ϵ=0.3时,ϵ=0.3>(1−α1)β=0.27,E2∗是渐近稳定的(见图9). 取α1=0.5,β=0.6,δ=0.24,A=0.2,µ=0.2,θ=0.01,则当取是渐近稳定的(见图10). 图4 α1=0.3,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.15时,(a)S,I,T的时间序列图和(b)I-T相平面图Fig.4.When α1=0.3,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.15,(a)time series graph of S,I,and T;(b)phase plan of I-T. 图5 α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.36时,(a)S,I, T 的时间序列图和(b)I-T 相平面图Fig.5.When α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.36,(a)time series graph of S,I,and T;(b)phase plan of I-T. 图6 α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.22时,(a)S,I, T 的时间序列图和(b)I-T 相平面图Fig.6.When α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.22,(a)time series graph of S,I,and T;(b)phase plan of I-T. 图7 当 T(0)不相同时,系统(2)的解趋于不同的边界平衡点(a)I 的时间序列图;(b)时间增加后 I 的时间序列图Fig.7.When T(0)is different,the solution of system(2)tends to the different boundary equilibrium:(a)Time series graph of I;(b)time series graph of I after time increment. 从图8—图10可看出,随着谣言的传播,易感者数量先减小后增大,谣言传播者的数量会先增大后减小,真实信息传播者数量逐渐增大,最后达到稳定状态.即系统(2)达到同时存在易感者、言传播者和真实信息传播者的稳定状态. 从图11(a)可以看出,真实信息传播者的初始值影响着谣言传播者的峰值以及谣言传播的时间,真实信息传播者的初始值越大谣言传播者的峰值越小,峰值到达的时间越早,谣言灭绝得越快.从图11(b)可以看出,谣言传播者的初始值影响着谣言传播者的峰值以及谣言传播者峰值到达的时间,谣言传播者的初始值越大谣言传播者的峰值越大,峰值到达的时间越早,但不影响谣言持续的时间. 图8 α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.3时,(a)S,I,T 的时间序列图和(b)I-T 相平面图Fig.8.When α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.3,(a)time series graph of S,I,and T;(b)phase plan of I-T. 图9 α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.3,δ=0.3时,(a)S,I,T 的时间序列图和(b)I-T 相平面图Fig.9.When α1=0.7,β=0.9,A=0.2,µ=0.2,θ=0.01,ϵ=0.3,δ=0.3,(a)time series graph of S,I,and T;(b)phase plan of I-T. 图10 α1=0.5,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.24时,(a)S,I,T 的时间序列图和(b)I-T 相平面图Fig.10.When α1=0.5,β=0.6,A=0.2,µ=0.2,θ=0.01,ϵ=0.01,δ=0.24,(a)time series graph of S,I,and T;(b)phase plan of I-T. 从图11(a)得到谣言传播者峰值Imax的散点图(见图12(a)),通过MATLAB拟合得到函数表达式:其中,x1=0.2881,x2=−20.11,y1=0.1296,y2=−6.828(结 果 见图12(b)),故T(0)与Imax之间的函数关系为Imax=0.2881e−20.11T(0)+0.1296e−6.828T(0),可以看出谣言传播者峰值Imax随着T(0)的增加按上述函数关系衰减. 图11 (a)不同真实信息传播者的初始值对谣言传播的影响;(b)不同谣言传播者的初始值对谣言传播的影响;参数取值α1=0.7,β=0.9,δ=0.36,A=0.2,µ=0.2,θ=0.01,ϵ=0.01Fig.11.(a)Influence of different initial values of true information spreaders;(b)influence of different initial values of rumor spreaders on the rumor propagation.The parameter values are α 1=0.7,β=0.9,δ=0.36,A=0.2,µ=0.2,θ=0.01,ϵ=0.01. 图12 (a)T(0)与谣言传播者峰值 I max 的散点图;(b)根据数据点拟合得到的曲线图Fig.12.(a)Scatter plot of T(0)and the peak value I max of rumor spreaders;(b)the curve graph of fitting data points. 本文在谣言传播模型中加入真实信息的传播者T,构建了SITR谣言传播模型,利用下一代矩阵得到了谣言传播的阈值K0,当K0<1 时,无谣言传播者无真实信息传播者平衡点存在,且是局部渐近稳定的.当K1>1 时,边界平衡点E1存在,若成立,则边界平衡点E1是局部渐近稳定的.当K2>1 时,边界平衡点E2存在,若K1 系统(2)中考虑了人口的移入和移出,所以人群构成的网络是一个动态网络,即网络中的节点和连边都是实时变化的,在动态网络中,新进入网络的个体的连边数目的分布(新个体的度分布)以及新节点与网络中已有节点的连边机制(随机连接、度优先连接、自适应连接等)等都影响着网络结构的变化,而网络结构又影响着网络上的传播过程,目前,网络动态的演化对网络上传染病的传播影响已有一些研究[25−27].如果考虑网络结构,需要考虑不同的新节点度分布,和新节点与旧节点的连边机制对网络结构的影响,然后再考虑不同情况下谣言传播的动力学行为,这是值得深入研究的内容,下一步我们将做这些方面的研究.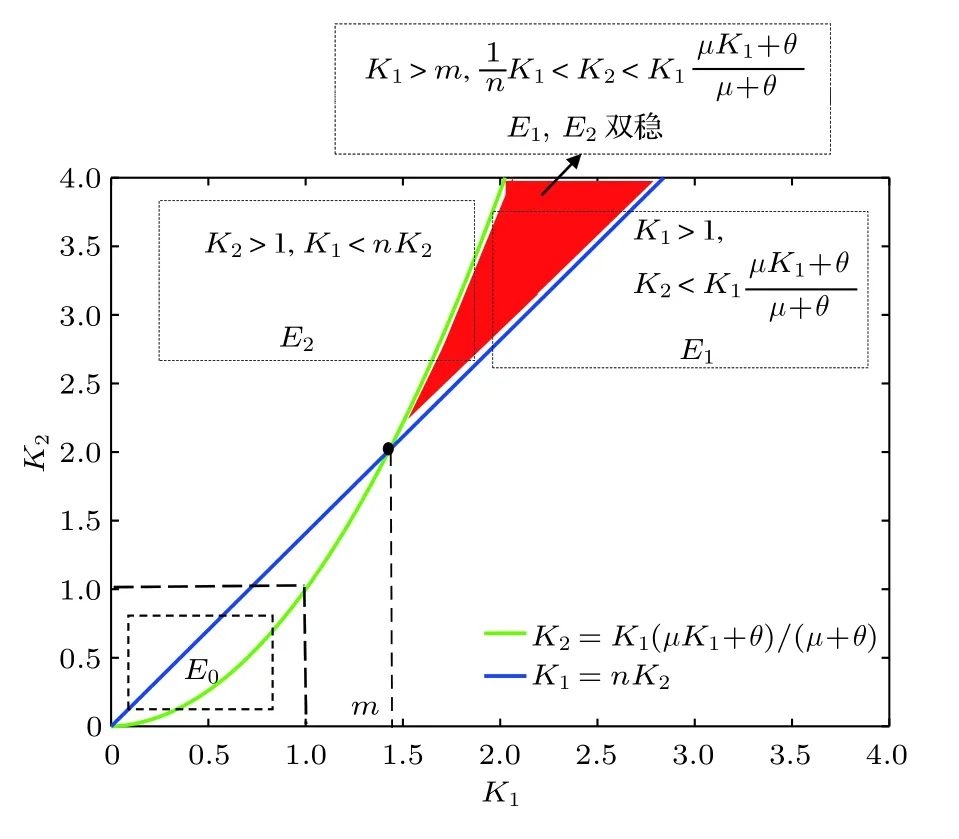
5 正平衡点的存在性及局部稳定性
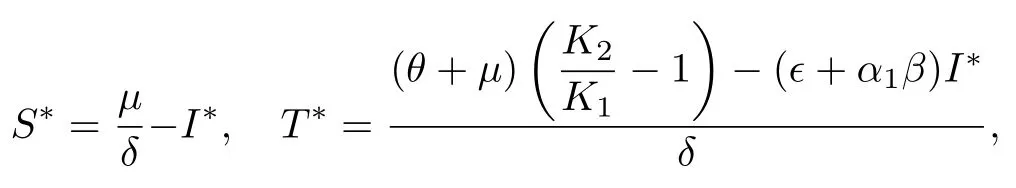
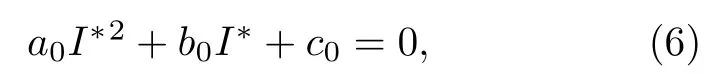

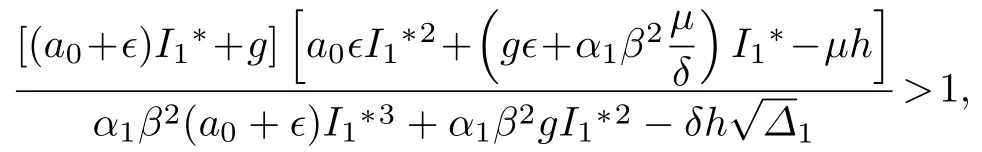

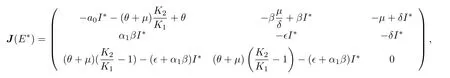



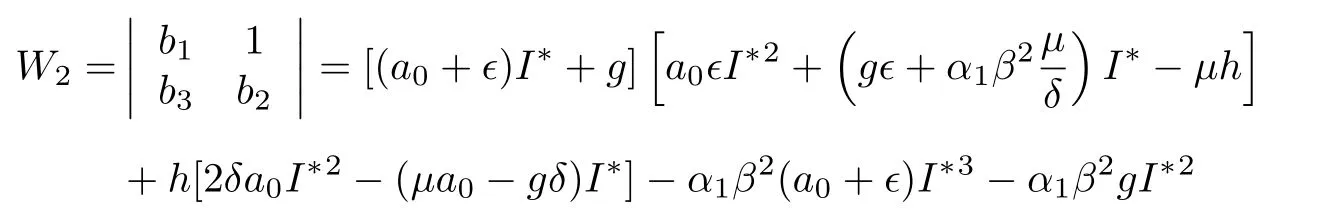
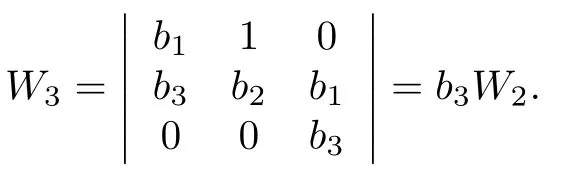

6 数值模拟





7 结 论
