关于非均匀系统局部平均压力张量的推导及对均匀流体的分析*

崔树稳 刘伟伟 朱如曾 钱萍

1)(沧州师范学院物理与信息工程学院,沧州 061001)

2)(中国科学院力学研究所,非线性力学国家重点实验室,北京 100190)

3)(中国科学院力学研究所,微重力国家实验室,北京 100190)

4)(北京科技大学数理学院,北京 100083)

1 引 言

对于平衡均匀无外场系统,Clausius[1]和Maxwell[2]基于维里定理,给出了压力公式:对于体积V中包含N个粒子的宏观体系,平衡后的压力为

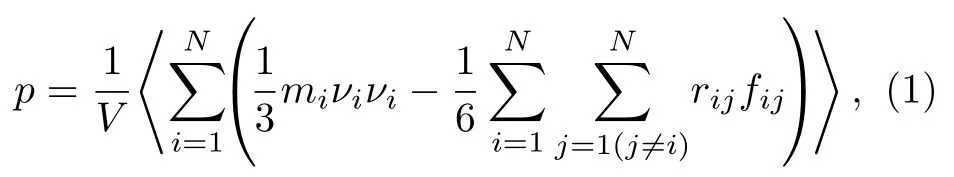
其中i,j表示粒子;mi是粒子i的质量;vi是粒子i的速度;rij是i,j之间距离;fij表示i,j之间的作用力,吸引力为正;〈 〉表示系综平均,也即时间平均.(1)式包含两部分,第一项是原子运动所贡献的压力,称为动压力,第二项源于原子之间的相互作用力,称为位形压力.

对于非均匀系统,例如气-液共存时的表面过渡层,压力应是张量,且与位置有关.应力张量分布函数σα,β(r)需要定义,使其满足连续介质的动量方程

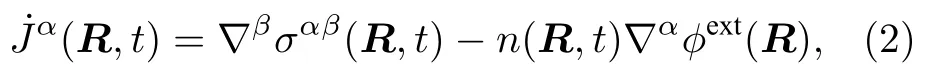
其中J是动量密度,n是粒子数密度,ϕext是外场势.Kirkwood和Buff[3]最早就对势情况提出空间点R处应力张量的构成方法.Irving和Kirkwood[4]给予更简洁的表述:作用在点R处面积元 dA上的力等于所有连线通过该面积元的分子对之间作用力之和,加上由于分子通过面积元 dA的运动在单位时间内交换的动量.Harasima[5]最早认识到满足连续介质动量方程(2)式的应力张量不唯一,并提出了另一种针对液体表面层构造应力张量的方法.Schofield和 Henderson[6]证明将 Irving和 Kirkwood定义中的分子对之间的连线改为曲线,其他不变,也是一种应力张量的正确构成方法,他们还给出了适合于多体势情况的应力张量的构成方法,使Irving和Kirkwood(IK)方法和Harasima方法成为他们的特例.显然,对于对势情况而言,IK 方法是最自然和最简单的,因而也是后来对势情况下,计算局部平均应力张量许多方案的基础[7,8].

对于由N个粒子组成的非均匀系统,从Irving和Kirkwood的定义很容易得到作为空间点(R)函数的压力张量的公式,

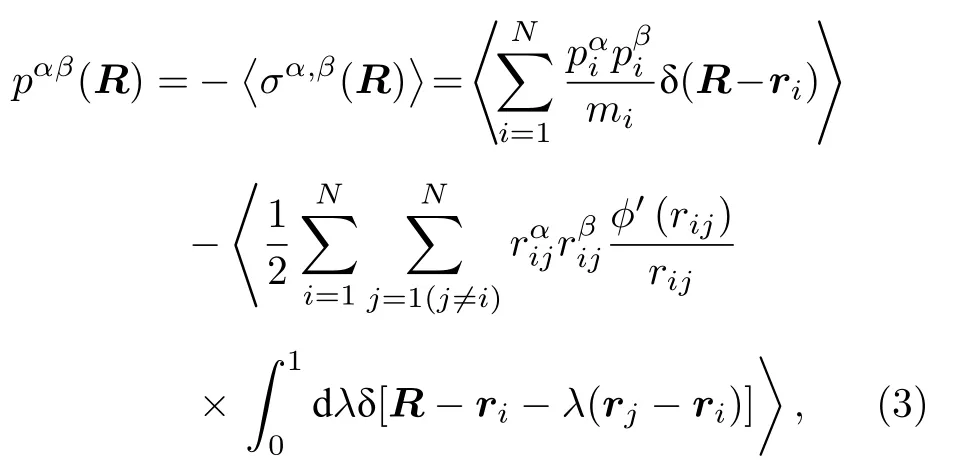
其中i,j表示粒子;α,β表示方向;mi是粒子i的质量;分别表示i粒子的动量在α,β方向的分量;表示矢量rj−ri在β方向上的分量;ϕ(rij)表示粒子i与粒子j之间的相互作用势.

(3)式的理论意义是显然的.但是由于其中含有d函数,不能直接用于实际测量和分子动力学模拟,所以被称为微观压力张量[9].Cormier等[9]采用傅里叶变换方法得到了(3)式的局部平均形式,即对于由N个粒子组成的非均匀流体中体积为V的局部小区域,平均压力张量为

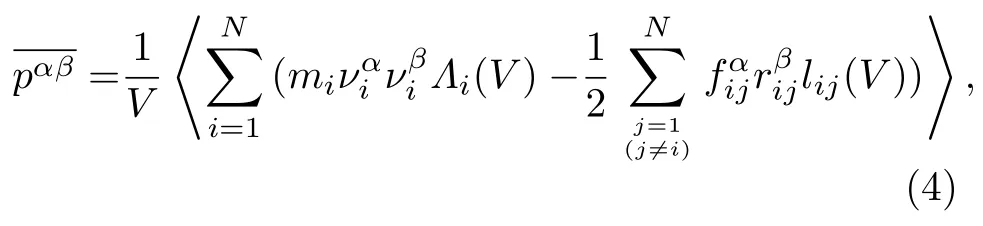
比较(1)和(4)式可知,就压力而言,它们表示的都是体积V中的平均值,区别在于前者的V是被刚性边界隔离着的均匀系统的总体积,而后者的V只是均匀或不均匀系统中的一小块的体积,所以两者明显不是等价的.一些研究者就非均匀系统中如果用前者代替后者将会引起的显著误差进行了讨论[10−12].

(4)式适用于固体、液体、气体等各种系统,因此应用价值十分广阔.例如Li等[13]采用巨正则蒙特卡罗方法模拟了超临界Lennard-Jones流体在纳米狭缝中的吸附行为,他们在(4)式中加进了壁-液势的影响项,这也相当于对(1)式做了修正,获得了吸附流体的压力.对于局部压力在原子量级的计算,一直是人们研究的热点,例如Torres-Sánchez等[14]以及Chen[15]对此进行了深入的研究.Yu和Jin[16]用硬核双Yukawa流体混合物模型研究胶体的热力学和结构特性时,在(4)式的基础上计算了胶体体系的主体相压力.

本文将用更为简洁的方法推导出适用于均匀、非均匀系统的局部平均压力张量普遍公式(4).鉴于在应用分子动力学计算(4)式时需要考虑计算耗时的最优化问题,但尚未见有关报道.作为一个最简例子,本文将给出均匀流体系统在以原子直径为长度单位的局部平均尺寸L∗较大条件下,局部平均位形压力中的三部分贡献项(体贡献项、面贡献项和线贡献项)与平均尺寸的关系式(含有待定参数),这是计算最优化方案的依据;以氩原子气体系统为例,用分子动力学模拟方法确定待定参数,并给出位形压力三部分贡献项在大尺寸和小尺寸L∗下各项行为的特点及温度的影响.这将为压力张量的分子动力学模拟计算时选项的最优化方法提供一个范例.

2 非均匀系统局部平均压力张量两种形式的简洁推导

2.1 第一种平均形式的推导

第一种平均形式就是(4)式.推导如下:将(3)式对局部小体积V求平均

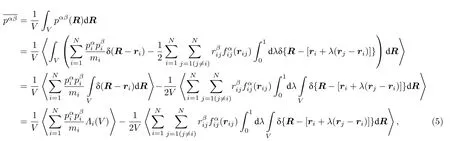
在(5)式中

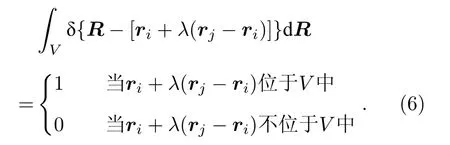
将(6)式代入(5)式即可以得到(4)式.(4)式包含两部分:第一部分是粒子的运动对压力的贡献,称为动压力,用表示;第二部分来源于粒子之间的相互作用,称为位形压力,用表示.

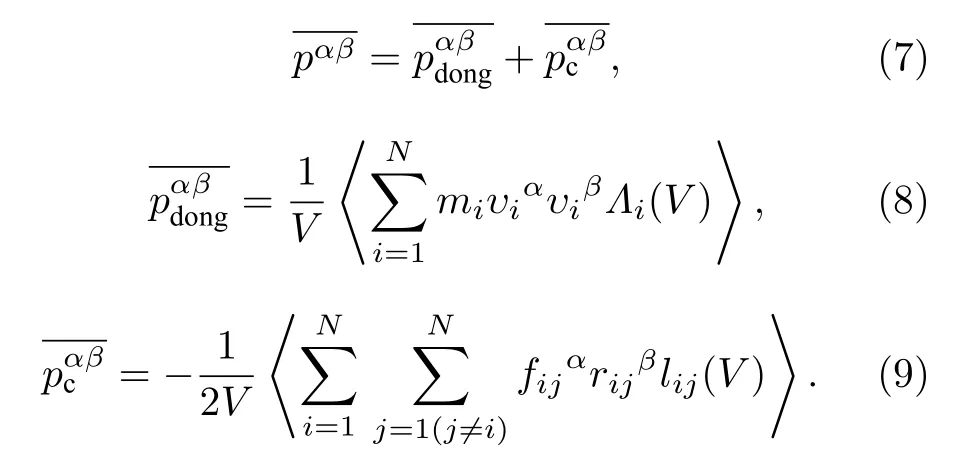
在各向同性的平衡条件下,(7)—(9)式可以简化为

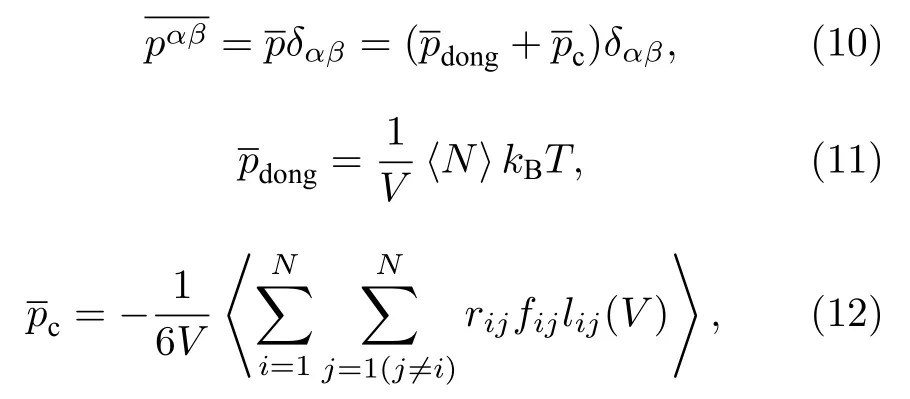
2.2 第二种平均形式的推导

在由N个分子组成的流体系统中,取体积为V的局部小长方体,如图1所示.设流体系统中分子对的联线与长方体V的交集,所形成的非零长度的线段的总数为所有这些非零长度线段所构成的集合记为于是(9)式可以改写为

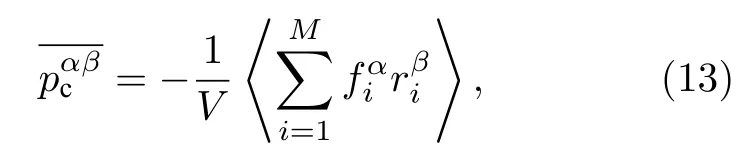
将(13)式代入(7)式,可以得到平均压力张量,

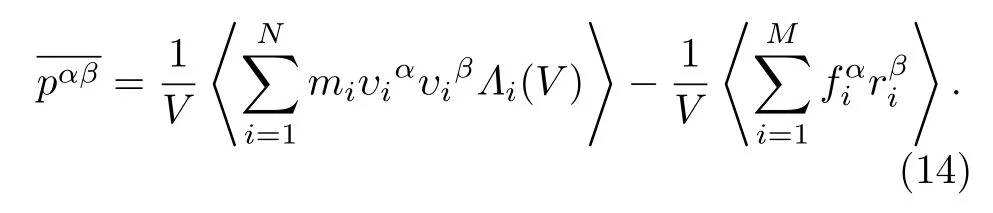
(14)式就是平均形式(4)的第二种表示形式.容易证明,(4)和(14)式中的体积V可以取任何形状,而不只限于长方体.只是要注意,此时一个分子对的联线与区域V所交的线段可以超过一个,求和时,应遍及全部线段.

图1 体积为 V 的长方体系统示意图Fig.1.Schematic figure of a rectangle with volume V.

3 均匀和非均匀系统位形压力张量局部平均形式的分析

3.1 理论分析

在由N个分子组成的系统(包括均匀系统和非均匀系统情况)中,取体积为V的小长方体,如图1所示.在(13)式中,对长方体V内的平均压力张量位形部分有贡献的粒子对中的两个粒子之间的距离必须小于分子间有效作用程长,其相对位置有三种主要情况:第一种是两个粒子都在长方体内,lij(V)=1,如图1所示;第二种是一个粒子在长方体内,一个在长方体外,lij(V)<1,如图2所示;第三种情况是两个粒子都不在长方体内,但交长方体的侧面于两点,lij(V)<1,如图3所示.三种情况的数量分别记为M1,M2,M3.

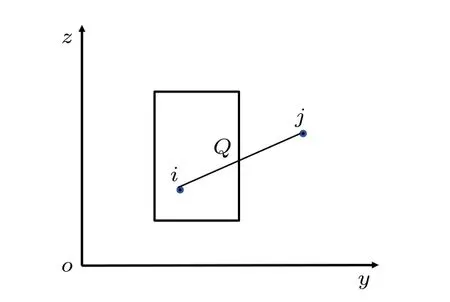
图2 一个粒子在 V 内,一个粒子在 V 外,只有一个交点示意图Fig.2.Geometry for calculating the contribution to the pressure from a pair of molecules i and j with only one intersection.

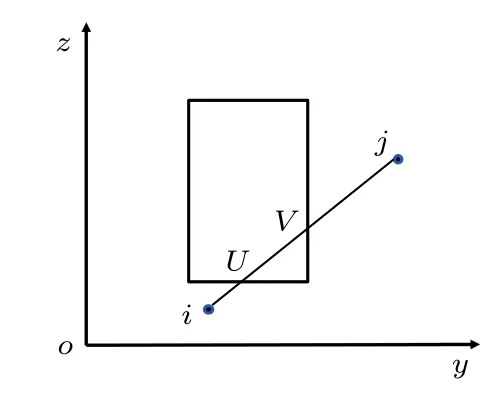
图3 两个粒子都在V外有两个交点示意图Fig.3.Geometry for calculating the contribution to the pressure from a pair of molecules i and j with two intersections.

粒子对中有至少一个粒子位于长方体V的边界面上或棱上的情况,虽然不是完全不可能,但是概率几乎为零,对计算平均位形压力的贡献可以忽略,故不计入.于是(13)式的求和上限M满足关系式

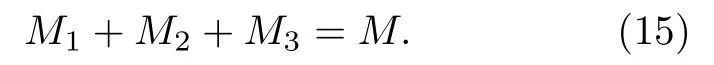
在长方体边长足够大,远超过分子间有效作用程长时,M1,M2,M3分别与长方体的体积、表面积及菱长近似成正比.为方便计算,无论长方体边长取多少,这些粒子对对位形压力张量的贡献都分别简称为体贡献、面贡献和线贡献

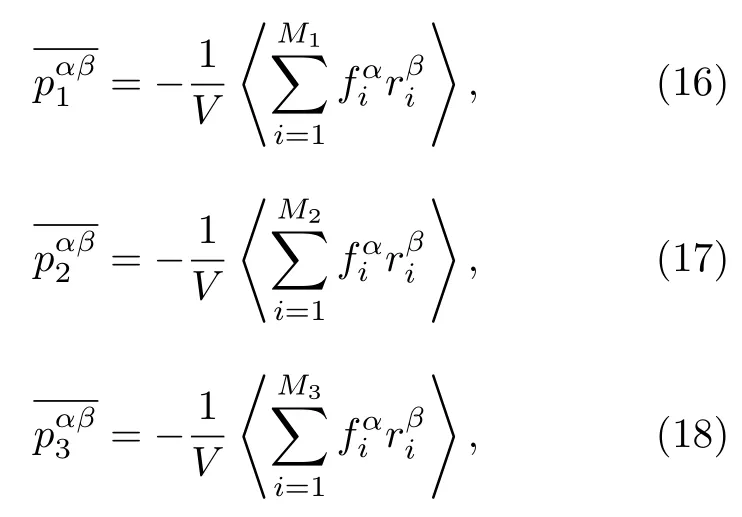
于是V中的平均位形压力张量总计为

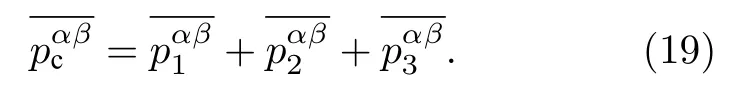
3.2 均匀流体系统位形压力三项贡献的分子动力学模拟

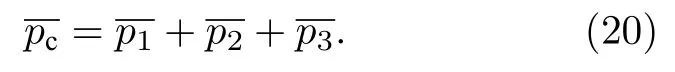
3.2.1 分子动力学模拟的方案

采用氩原子的平衡系统作为研究对象进行模拟和分析.氩的初始位型采用简立方的点阵结构,原子间距1.2σ.模拟体系尺寸为:x×y×z=18σ×18σ×18σ,x,y,z方向上均采用镜像边界条件.氩原子之间采用截断距离为 3σ的Lennard-Jones势能函数来描述

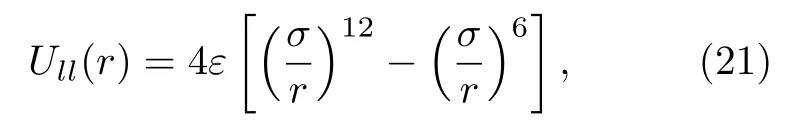
其中ε为势能参数,σ为原子直径,r为原子中心之间的距离.对于氩原子σ=0.3405 nm,ε=kB×120 K,其中kB=1.38×10−23J/K.

模拟中采用无量纲化量,分别以σ,ε和氩原子的质量m=6.63382×10–26kg 作为长度、能量和质量单位.经过无量纲化之后,给出了其他物理量的标度:比如温度的无量纲量T∗=kT/ε,180 K相当于 1.5;时间的无量纲体系的演化采用 Velocity-Verlet方法,截断长度rcutoff=3.0σ,弛豫过程采用温度为180 K的NVT系综,时间步长取 δt=5 fs,弛豫 50 万个时间步.在达到迟豫平衡之后,采用累积平均方法计算物理量的时间平均值

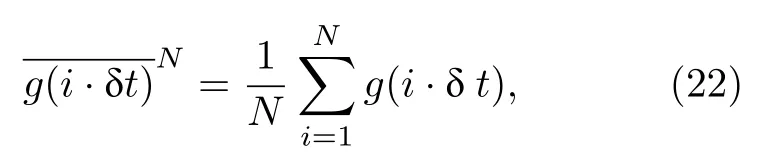
3.2.2 模拟结果

在180 K下的氩系统弛豫平衡后的100万时步内,在体系中取边长L∗不同的立方体,对相关物理量分别进行统计平均,得到该温度下各个尺寸的列于表1中.L∗3与立方体含有的粒子平均数成正比.的关系如图4所示.

表1 ,,和的模拟值Table 1. Values of,, and given by simulation.

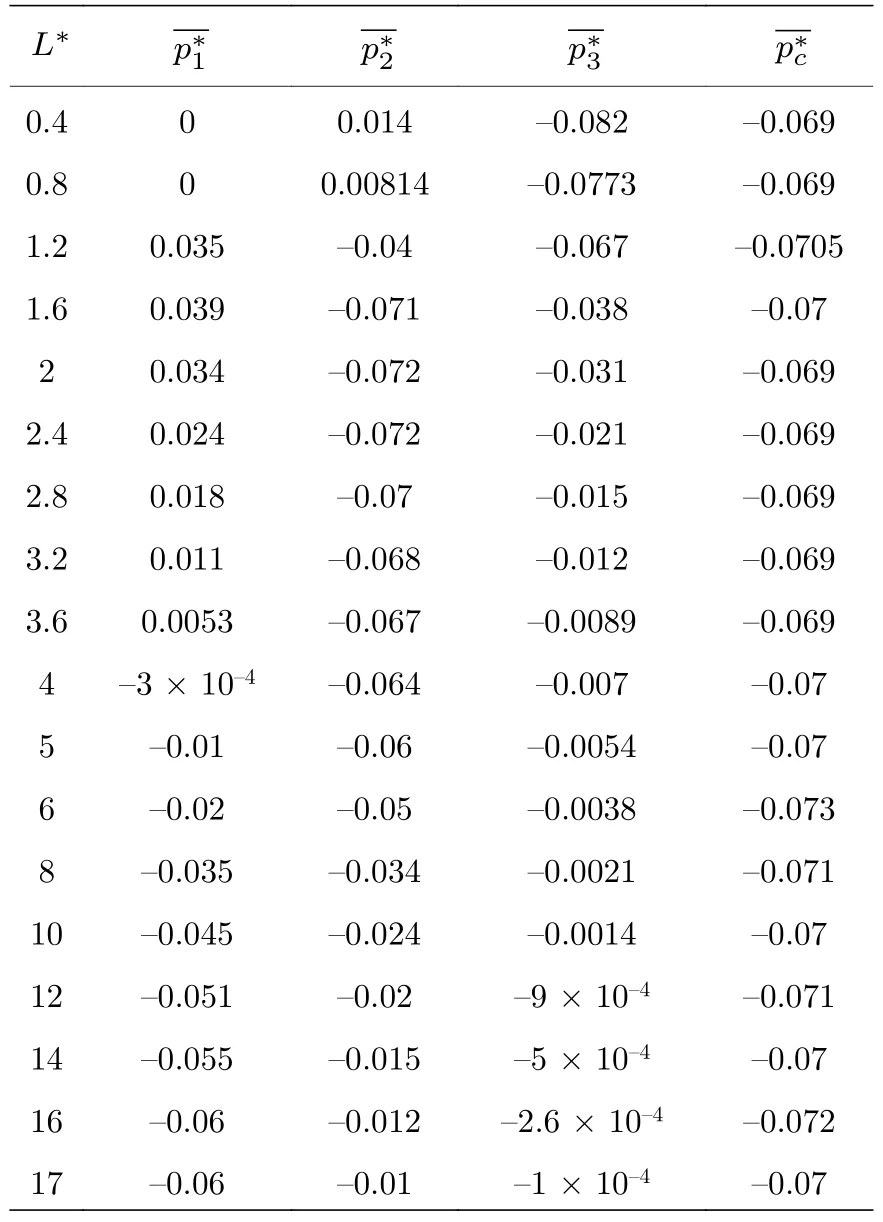
表1 ,,和的模拟值Table 1. Values of,, and given by simulation.

L∗p∗1 p∗2 p∗3 p∗c 0.4 0 0.014–0.082–0.069 0.8 0 0.00814–0.0773–0.069 1.2 0.035–0.04–0.067–0.0705 1.6 0.039–0.071–0.038–0.07 2 0.034–0.072–0.031–0.069 2.4 0.024–0.072–0.021–0.069 2.8 0.018–0.07–0.015–0.069 3.2 0.011–0.068–0.012–0.069 3.6 0.0053–0.067–0.0089–0.069 4–3×10–4–0.064–0.007–0.07 5–0.01–0.06–0.0054–0.07 6–0.02–0.05–0.0038–0.073 8–0.035–0.034–0.0021–0.071 10–0.045–0.024–0.0014–0.07 12–0.051–0.02–9×10–4–0.071 14–0.055–0.015–5×10–4–0.07 16–0.06–0.012–2.6×10–4–0.072 17–0.06–0.01–1×10–4–0.07

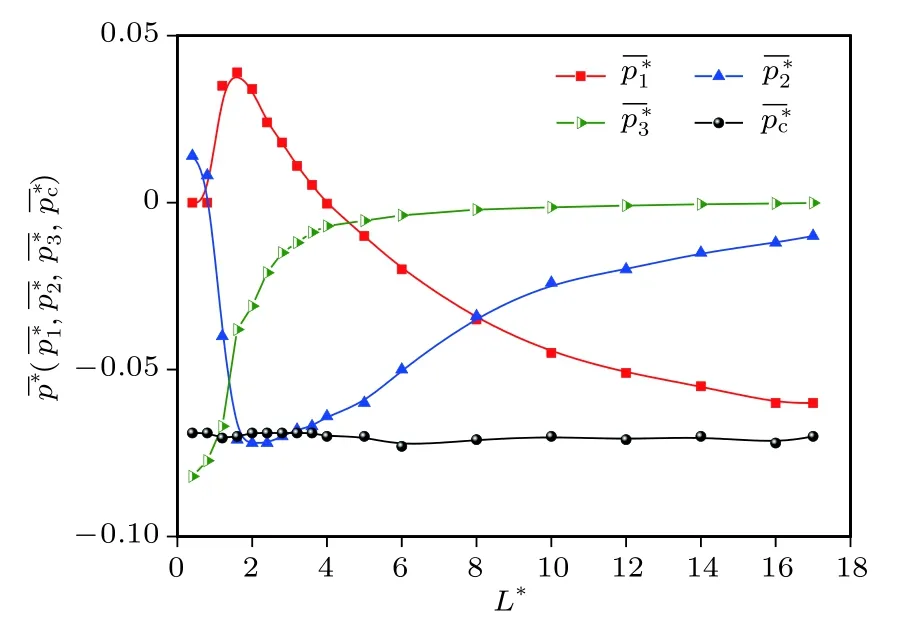
图4 ,,, 与 L ∗ 的关系Fig.4.Relation between ,,, and L ∗.

3.3 均匀流体位形压力三部分贡献的尺度分析

3.3.1 大L∗分析

随着所取平均体积的大小不同,(14)式中的平均动压力保持不变,平均位形压力包含的三项相对大小会有很大不同.弄清楚它们与计算尺度L∗的关系,对于我们在实际应用中节省计算机时非常重要.在L∗较大,即L∗>8 的情况下,首先分析位形压力中与L∗之间的依赖关系,再分析与L∗之间的依赖关系.

面贡献为

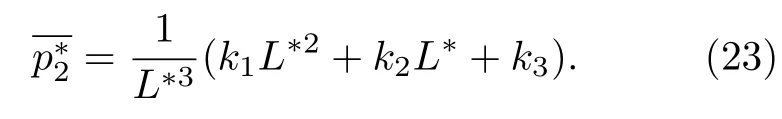
此式右边括号中的第一项的来源是,在大L∗条件下,作为近似,可以先不考虑棱对面贡献的影响,根据(17)式,面贡献与体积的乘积应与第二种粒子对数M2成正比,故与V的总面积,即与L∗的平方成正比.由于此情况下计算的面贡献没有考虑棱对面贡献的影响,计算的面贡献与实际的面贡献有差别,因此应该校正这样计算的面贡献:先不计棱两端的端点效应,棱效应与体积的乘积应与棱长,即边长L∗成正比,这就是(23)式中的第二项.依此类推,还应加上顶角的影响,即第三项它与L∗无关,是个待定常数.k1,k2,k3是与具体的系统和条件有关的常数.

线贡献为

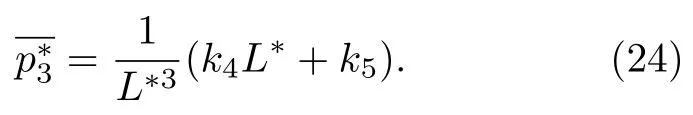
此式右边括号中的第一项的来源是,在大L∗条件下,作为近似,可以先不考虑顶角对线贡献的影响,依据(18)式,线贡献与体积的乘积,与M3成正比,故与V的边长,即与L∗成正比.这样计算的线贡献与实际的线贡献有差别,因此要加上顶角端点的影响,即第二项k5.k4,k5是常数,由具体的系统和条件决定.

根据力学平衡条件,总平均压力与所取的L∗无关,由(11)式可知,平均动压力也与L∗无关,所以总平均位形压力与所取的L∗无关.平均位形压力的体贡献可以表示为

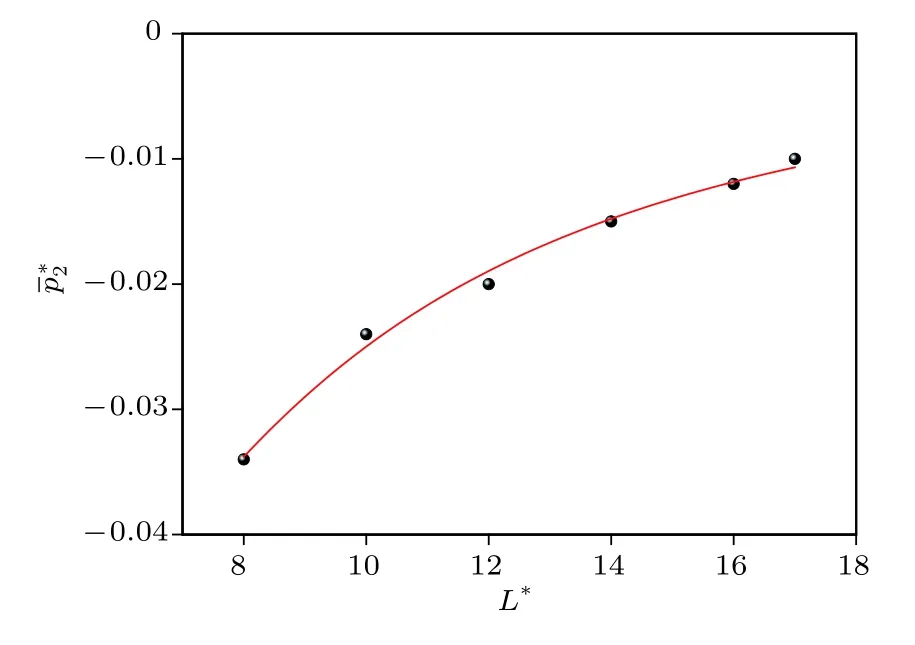
图5 的拟合曲线Fig.5.Fitting curve of.

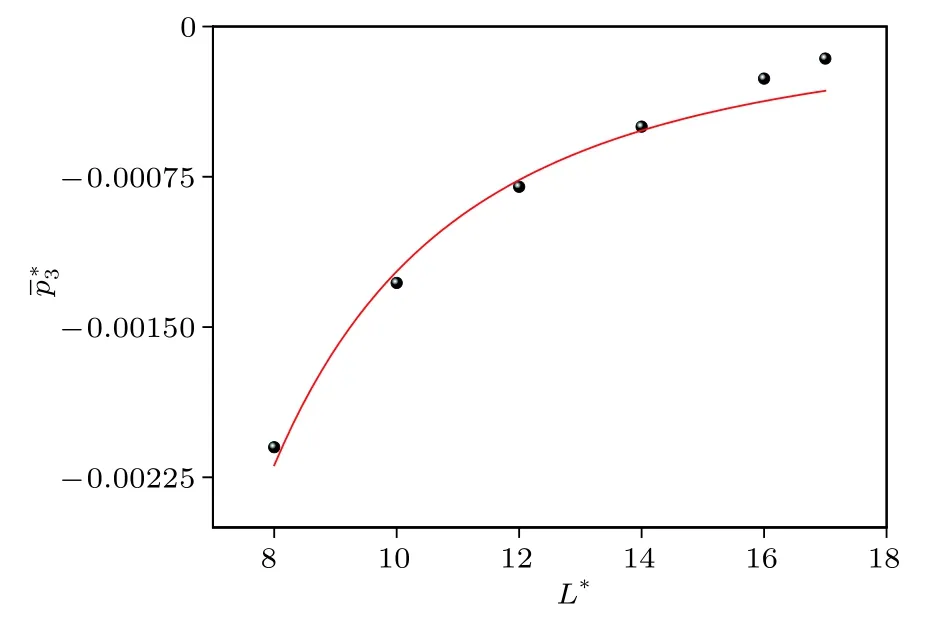
图6 的拟合曲线Fig.6.Fitting curve of.

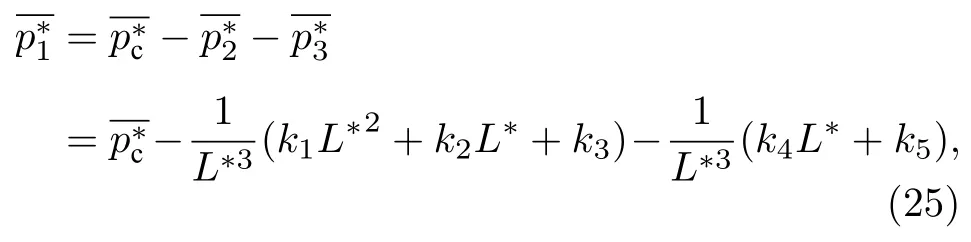
对于本文模拟的平衡态氩系统,取L∗较大时对应的分子动力学模拟值,进行拟合,结果给出:k1=0.24053,k2=−0.01509,k3=0.0345,k4=0.10328,k5=−0.02699,如图5和图6所示.

上述三个方程(23),(24),(25)与分子动力学结果拟合的方差都很小,这也证明了本文的尺度分析和推理是正确的.

3.3.2 较小尺度分析

从氩系统的模拟结果图4可以看出,在L∗≤4区域,三种贡献的行为有些复杂,其中特征及物理根源分析如下.

虽然上述分析是对氩系统而言,但除去具体的数字k1,k2,k3,k4,k5及大小尺度L∗分界线可能不同外,所有定性性质对其他系统不会有实质改变.

分析结果对于正确取舍三部分贡献是重要的.一些文献[6−8,12]直接将宏观大体积整体平均定理(1)式用到局部小体积上是不准确的.原因是:1)遗漏了线贡献和面贡献;2)即使对(1)式做了修正,没有遗漏面贡献,对于面贡献项,都用 1/2代替了(4)式右边的lij(V),即用分子对距离的一半在β方向的投影代替了(17)式中的.对于第1)点,只有当L∗远远大于分子有效作用距离时,这种遗漏才不会带来明显的误差;对于第2)点,仅对分子有效作用距离范围内密度均匀的情况适用,此时lij(V)的统计平均值为1/2.

3.4 温度对位形压力的影响

在讨论界面特性及气液固相变过程中,需要研究界面压力张量及表面张力随温度的变化情况[7,8].因此本节采用分子动力学模拟,进一步研究了温度对氩系统位形压力的影响.分子动力学模拟的细节与 3.2 节相同,取L∗=6,温度取值范围T∗=1.4—2.3,模拟结果如图7所示.

从图7可以看出,位形压力随着温度的升高而升高.这是由于温度升高,分子平均动能增加,使得粒子对处于高斥力区(rij<σ)的概率增加,斥力增大,从而位形压力增高.

4 结 论

对于平衡的非均匀系统,人们推导了局部平均压力张量的表达式.本文用更为简洁的方法推导了这一表达式.此表达式也适用于均匀流体系统.本文给出在局部平均尺寸L∗>8 的条件下均匀流体系统平均位形压力中的三部分贡献项(体贡献项、面贡献项和线贡献项)与L∗的理论关系式(含有待定参数),并以氩原子气体系统为例,在温度180 K,原子数密度 0.8σ−3下,对分子间采用林纳德-琼斯势进行了分子动力学模拟,给出了条件下三项贡献及总位形压力的模拟曲线,确定了L∗>8条件下理论关系式中的待定系数,并做了大L∗和小L∗下各项行为的特点分析和温度影响的模拟分析,得到L∗足够大,才可以忽略面贡献项和线贡献项,在纳米尺度下,忽略面贡献项和线贡献项,也就是忽略边界效应会给计算带来明显的误差.这些结论对于压力张量的分子动力学模拟计算时选项的最优化是有意义的.