斜交网筒结构抗侧刚度影响分析

廖文翔， 何广杰

(西南交通大学， 四川成都 610031)

网格筒体系是由剪力墙围成的核心内筒和斜交网格形成的外筒以及楼板连接形成筒中筒的新型结构体系[1-3]。其中斜交网格外筒是由斜柱和环梁构成的，相比传统的框架外筒更具有适应高烈度地震区的能力，优于斜柱的拉压刚度远大于抗弯刚度，因此斜柱不仅能够提供较大水平抗侧刚度，同时也提供了较大的抗弯刚度，在高层以及超高超限的B类建筑的建造中具有非常大的优势。与传统结构相比斜交结构的受力性能，传力路径和机理等都存在着显著的差异。外筒的斜柱将楼层的竖向重力荷载和横向水平荷载都转化成为了斜柱的拉压轴力向着下层传递，因此斜交结构不仅有着很强的空间协同工作的性能，同时斜柱之间必须要传力可靠。斜柱的水平抗侧刚度大于传统结构，甚至有可能超过核心筒体。而且这类新型结构和传统结构体系相比在进入弹塑性后体系的屈服机制也不同，抗震防线在连梁屈服后的第二阶段内力重分布也发生了较大的变化，因此了解此类结构的刚度分配，分析体系的抗侧刚度以及塑性发展趋势，探讨体系的抗震屈服机制是进行抗震概念设计的必要前提。

目前我国的斜交网格新型结构体系多建造在经济较发达并且处于抗震设防高烈度的区域，建筑结构的安全是结构设计的重点。但是，目前该类新型结构体系既没有经受大震的考验，也没有十分丰富的工程经验，相关理论远落后于工程实践。因此本文在控制外部框筒用钢量相同和内部剪力墙不变的条件下将斜交网格核心筒和传统框架核心筒在地震作用下的优劣表现形成对比，分析新型结构的优势。并且通过改变斜柱水平相交角度判断该类参数对结构水平抗侧刚度变化影响，探讨这类新型体系结构体系在罕遇地震作用下的塑性铰发展趋势有着重要的意义，同时这也是结构合理设计、概念设计重要的前提。

1 分析模型及方法

1.1 分析模型

本文参考实际的工程，并结合斜交网格核心筒的受力特征[4-6]和本文的研究目的设计了结构布置规则并带有角柱的斜交网格核心筒结构。其中内筒为剪力墙围成的核心筒，混凝土强度等级为C60，剪力墙截面自下而上均采用500 mm的墙厚，连梁的厚度同所在楼层的剪力墙厚度，连梁高度为1 200 mm；外筒斜柱为圆钢柱，直径根据同直框架的用钢量相等原则进行换算，并且直框架核心筒圆钢柱直径取为1 200 mm，角柱采用1 500 mm；内外筒之间的连系梁采用型号为600 mm×200 mm×11 mm×17 mm的工字钢，外筒环梁采用型号为800 mm×300 mm×20 mm×40 mm的工字钢，钢材强度均采用Q345。不同模型的剪力墙内筒的墙厚和墙肢以及布置均不变。内外筒之间的连系梁、交叉斜柱之间以及斜柱与环梁之间均采用刚性连接，为了简化计算楼板采用刚性楼板假定。同时由于常见高层建筑结构体系的高宽比较大，为了更好地发挥内外筒体之间共同工作的空间能力，因此在不同模型中均选用高宽比为6的斜交网格核心筒体结构。结构采用3.6 m的层高，共45层，总高度为162 m，外筒体为边长30 m的正方形外筒，内筒为15 m的正方形内筒。为对比斜交网格体系和传统框架体系的抗震性能，以及不同斜交角度下对抗侧刚度的影响，通过在不改变剪力墙核心筒布置、角柱以及环梁截面的基础上，控制每层斜柱的用钢量同直框架柱相等的原则进行换算，来确定不同斜交角度的模型采用不同的斜柱截面尺寸。所有斜柱角度模型的斜柱截面经过验算均满足结构构件强度、刚度和稳定性的要求。斜交网格结构外网筒的布置形式如图1所示，除斜交角度外，其余参数均保持不变。

图1 不同斜柱角度网格布置形式

1.2 分析方法

本文所用模型采用GB 50009-2010《建筑结构荷载规范》设置结构的竖向重力荷载和水平风荷载以及地震作用。其中楼板与梁柱构件的自重由SAP2000有限元软件根据材料的截面设定自动进行计算。考虑到楼层板面的建筑做法以及外墙和隔墙的作用取楼面均布恒荷载为3.5 kN/m2，楼面活荷载按普通办公楼设为2 kN/m2。风荷载设定按B类地面粗糙度，体形系数取为0.5，基本风压为0.3 kN/m2，结构阻尼比为0.04，地震作用按照GB 50011-2010《建筑抗震设计规范》规定取8度二类场地，地震分组为二组，设计基本加速度为0.2g，特征周期为0.4 s，考虑到填充墙的影响周期折减系数取0.9，模型分析方法采用振型分解反应谱法进行弹性分析计算，其中结构的质量源设定为1.0×恒载(包括自重)+0.5×活载。分析计算过程中考虑上述荷载的组合效应，采用规范上的地震设计组合为：1.2×(恒荷载+0.5×活荷载)+1.3×地震作用+1.4×风荷载对结构的变形进行统一的提取分析。分析程序采用SAP2000，其中剪力墙采用分层壳单元模拟，剪力墙中的约束混凝土采用程序自带的Mander约束混凝土应力应变曲线本构关系[7]，斜柱、环梁以及连系梁均采用框架单元进行模拟，其中钢材的本构关系采用二折线的弹塑性应力-应力应变曲线本构关系。

2 分析结果对比

模型使用振型分解反应谱的方法对结构进行分析，不同模型斜柱的直径按照用钢量相等的原则进行设置。在改变斜交角度后，通过有限元分析计算后得到结构前三阶自振周期如下表1所示，由表1可以看出模型的前两阶振型分别以X向和Y向平动为主，第三振型为扭转。不同斜交角度斜交结构体系的第一自振周期均小于传统的框架剪力墙核心筒结构，并在70 °附近自振周期达到最小值，此时结构的抗侧刚度最大。这说明在高烈度地区斜交结构有更好的适应性和抗震能力。结构斜交角度在35 °附近时，抗震性能表现比传统结构差，这是因为随着斜交角度的减小，斜柱的轴向刚度在竖向的分量也在减小，因此结构的抗侧刚度总体呈减小的趋势导致结构周期变大。除了35 °外斜交网筒结构的表现都比框筒结构优异。并且斜交网筒体结构均有着更好的抗扭刚度，随着斜交角度的增大，在55.2 °附近，第三自振周期达到最小，此时斜交结构的抗扭刚度达到最大。

由图2可以看出顶层位移和最大层间位移角在斜交角为70.8 °附近时达到最小值。这说明高宽比大于6.0时，带有角柱的斜交结构在70.8 °附近时结构达到最优。此时抗侧刚度最大，结构在相同地震作用下顶点位移最小，同时最大层间位移角也为最小。并且当斜交角度大于55 °时，斜交结构抗侧刚度和抗扭刚度均优于传统框架剪力墙核心筒。当在35 °附近时，斜交结构的顶点位移和最大层间位移角均大于传统框架剪力墙核心筒结构，此时斜交外筒结构已经失去了应有的抗侧优势。

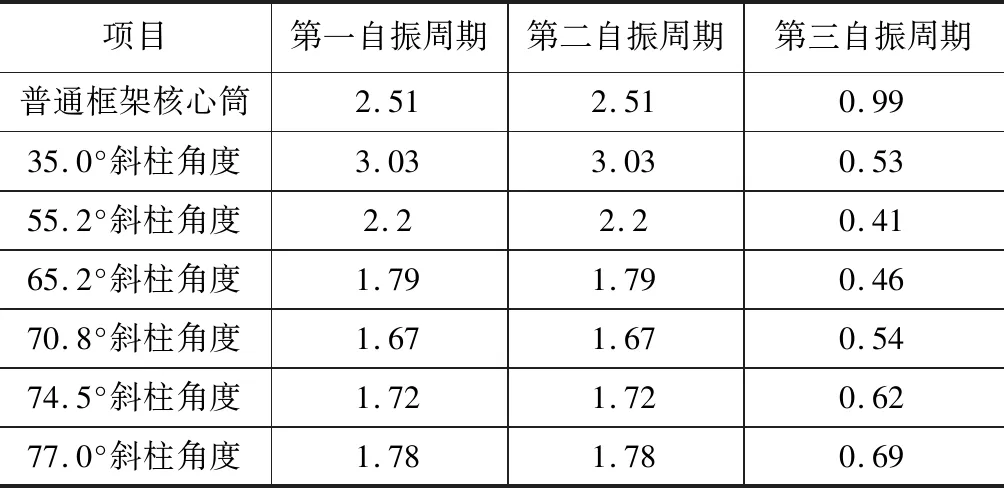
表1 结构前三阶自振周期 s

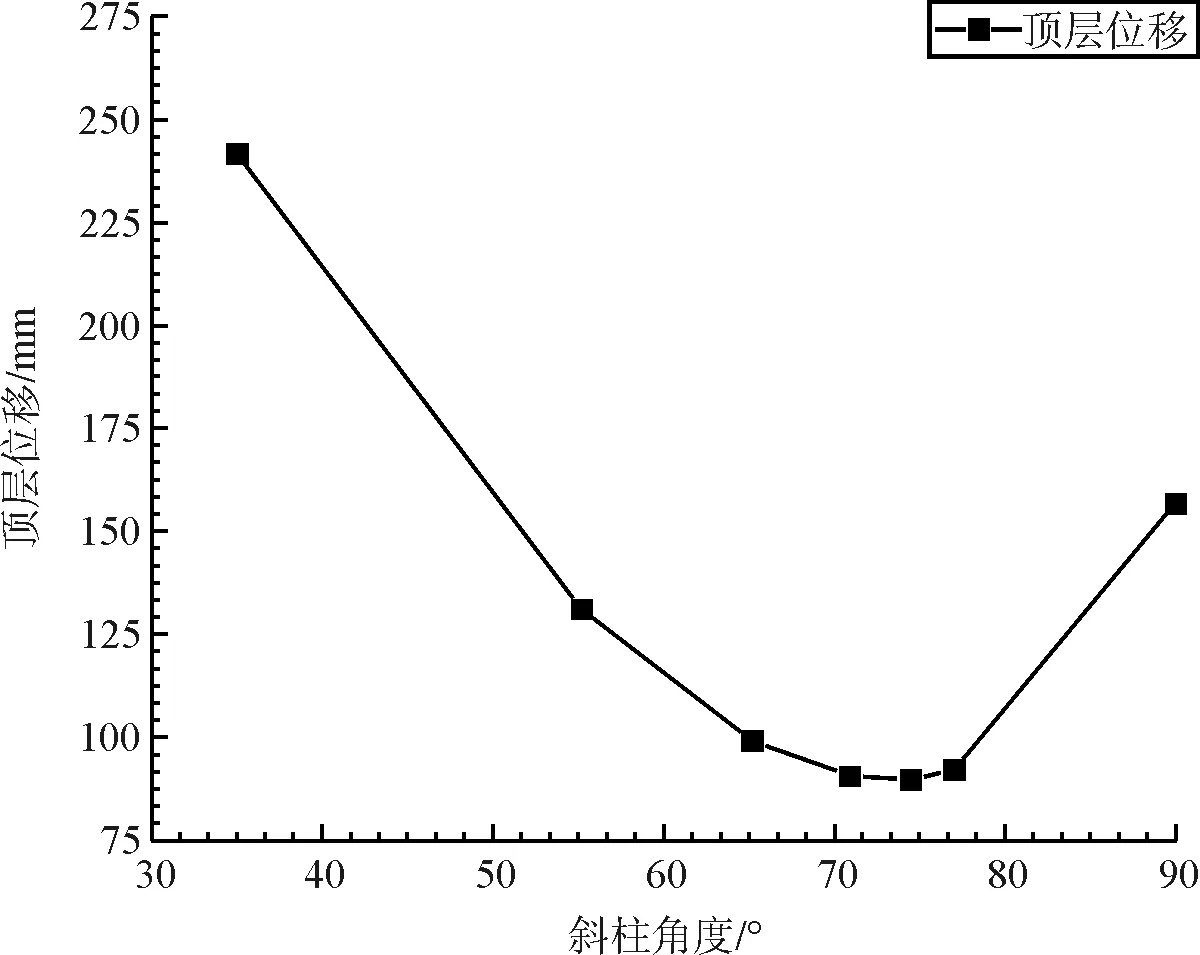
(a)顶层位移

(b)最大层间位移角图2 不同斜交角度顶层位移及最大层间位移角

3 结论

(1)在用钢量相同的前提下，斜交角度大于55 °的斜交结构抗侧刚度大于传统的框架剪力墙结构，所有的斜交网格核心筒结构的抗震性能表现都要比框架核心筒结构优异。这意味着在频遇地震作用下，斜交结构的变形要小于传统结构，斜交结构具有更好的抗震性能和抵抗结构变形的能力。剪力墙核心筒仍然是在弹性阶段抵抗地震力的关键构件，当处于35～55 °之间时，抗侧刚度小于传统结构，这说明斜柱扭曲的程度越大，抗侧刚度降低的越加明显。

(2)分析结果表明对于45层带有角柱的斜交网筒结构，斜交最优角度在70 °附近，此时斜交网格结构弹性阶段的抗震性能最好，并且最大层间位移角和最大顶层位移均为达到最小。并且当在55.2 °附近时，结构的第三周期最短，此时斜交结构的抗扭刚度最大。

(3)斜交结构的抗扭刚度和抗侧刚度要远大于传统的框架核心筒体结构，这有利于改善不规则结构的位移比，同时在实际工程应用中应该主要考虑斜交结构的设计应由强度控制而不是变形控制。斜交结构在提高抗侧刚度的同时，其在塑性阶段的延性也相应的降低，因此斜交结构在塑性阶段应该以改善结构的变形能力为主。