基于蚁群算法的MIG焊脉冲电流PID参数优化研究

薛家祥，张俊红

（华南理工大学 机械与汽车工程学院，广州 510640）

传统的比例积分微分PID（proportional-integralderivative）控制是最早的控制策略之一，由于使用简单，被广泛运用于各种控制过程中[1-3]。然而，PID控制也存在一定的不足，如Z-N（Ziegler-Nichols）法整定出的PID参数不能自适应，致使控制效果不佳。因此有必要寻找一种智能PID参数优化控制方法。目前，已经发展出了很多智能PID优化方法，包括遗传算法、模糊算法、粒子群算法等[4-5]。这些算法具有超调量小、收敛速度快和鲁棒性好等优点，但仍然存在一些问题，比如容易陷入局部收敛等。

在此以MIG（metal inert-gas）焊脉冲电流为研究对象，采用基于蚁群算法ACO的PID参数优化控制，进而达到快速控制MIG焊脉冲电流的效果。蚁群算法主要利用正反馈原理对参数进行全局寻优搜索，根据MatLab/Simulink仿真结果表明，该方法具有快速收敛、超调量小等优点。

1 MIG焊脉冲电流

脉冲MIG焊电源框图如1所示。其工作原理是：将工频为50 Hz，380 V的三相工业用电经过整流滤波，再对滤波后的直流电进行IGBT全桥逆变，输出中频交流电，使用中频变压器将中频交流电变成低电压大电流。然后进行二次整流滤波，最终输出低电压大电流的MIG焊电流。过程由主控芯片TMS320F280049控制IGBT的开通与关断，合理控制开关管的通断产生MIG焊脉冲电流。脉冲电流示意图如图2所示。

图1 MIG焊电源Fig.1 MIG welding power supply

图2 脉冲电流Fig.2 Pulse current

2 蚁群算法

蚁群系统ACS（ant colony system）由意大利学者Dorigo，Maniezzo等人首先提出[6]。他们发现单个蚂蚁的智力平平，但是蚁群整体会体现一些智能的行为，蚂蚁觅食过程中，如果在蚂蚁和食物源之间设置障碍，蚂蚁能发现并最终选取最短路径寻觅食物。研究发现，蚂蚁会在其经过的路径上释放一种可以称之为信息素（pheromone）的物质，蚂蚁对信息素有感知能力，会往信息素多的地方走，每只蚂蚁都会留下信息素，形成一种正反馈机制，经过一段时间，蚁群就会找到到达食物源的最短路径。

蚂蚁觅食过程如图3所示。在洞穴和食物之间有一障碍物，蚂蚁如果想得到食物有2条路径：A→C→B和A→D→B。由图3a可见，刚开始蚂蚁在路径A→C→B和路径A→D→B上是均匀分布的。但是，每只蚂蚁经过路途都会留下信息素，因为路径A→C→B比路径A→D→B的距离要短，所以经过一段时间路径A→C→B上的信息素会比路径A→D→B上的多，就会吸引更多蚂蚁从路径A→C→B去寻找食物，如图3b所示。随着时间的推移，路径A→C→B上的信息素会越来越多，吸引更多的蚂蚁，最终确定蚂蚁行走的最短路径，如图3c所示。

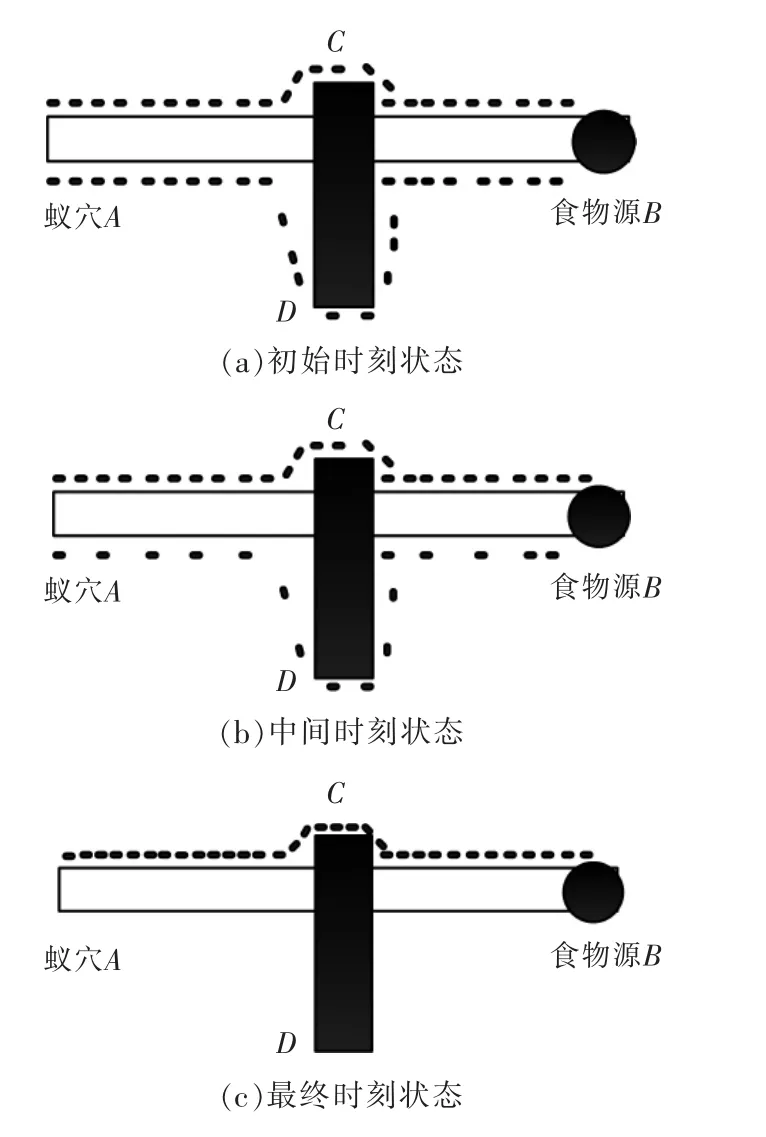
图3 蚂蚁觅食过程Fig.3 Ant foraging process

由上述蚂蚁找食物模式演变而来的算法，即为蚁群算法。该算法具有信息正反馈机制等特征，是一种启发式全局优化算法[7]。

3 基于蚁群算法的PID参数控制

PID控制原理如图4所示。

图4 PID控制系统原理Fig.4 PID control system principle

PID控制是一种线性控制，通过控制给定值与实际输出值的偏差来对被控对象进行控制。PID控制规律为

式中：Kp为比例系数；Ki为积分系数；Kd为微分系数。这3个参数的选择共同决定了PID控制系统的稳定性和有效性，经典的PID参数的选定常采用试凑法，效果难以保证，无法自适应。

采用蚁群算法的系统结构框图如图5所示。该系统主要包括2个部分，PID控制器和蚁群算法。系统采用蚁群算法不断优化更新PID参数，直至达到最优控制。

图5 蚁群算法系统结构Fig.5 Structure of ant colony algorithm system

3.1 节点生成与参数表示

对 PID 控制的 3个参数 Kp，Ki，Kd进行优化，都保留4位小数，每个参数需由5个数字表示。定义：在xOy平面内，将参数 Kp，Ki，Kd抽象为平面内的点；横坐标 x1～x5，x6～x10，x11～x15分别为 Kp，Ki，Kd的数位；横坐标选取 1～15，纵坐标选取 0～9，则在平面xOy上有150个节点。假设，有m只蚂蚁，蚂蚁的行走路径为 path（i）＝｛y1，i，y2，i，…，y15，i｝，i＝1，2，…，m。 其中，path（i）为第 i个蚂蚁爬行路径；yj，i为第 i只蚂蚁爬行对应的纵坐标值。蚂蚁爬行路径优化后如图6所示。

图6 第i只蚂蚁爬行路径示意图Fig.6 Ant i crawling path diagram

参数 Kp，Ki，Kd可由该路径表示为

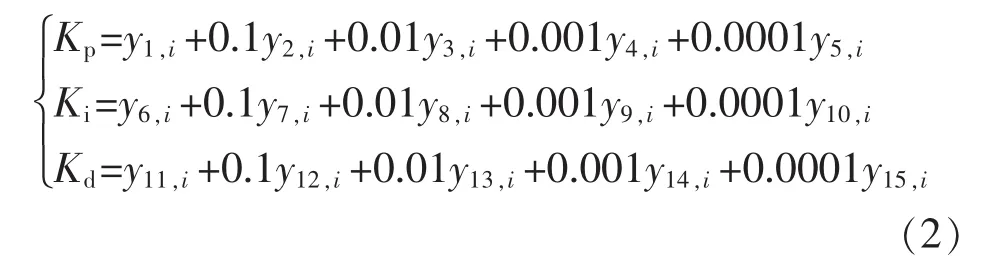
根据图 6 以及式（2）求得，Kp，Ki，Kd分别为3.4344，6.7675，8.5336。 为了加快蚁群算法的收敛速度，可以根据所求得的Kp，Ki，Kd值缩小搜索范围。按照式（3）进行限定，即

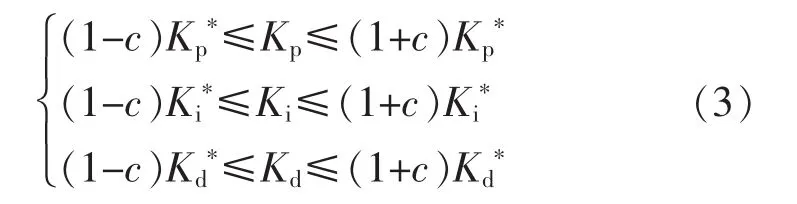
式中：c为收敛因子，其取值范围为 0＜c＜1。

3.2 路径选择与确定目标函数

由于蚂蚁对路径的选择取决于路径上的信息素，所以可以算得蚂蚁i在t时刻由节点m转移到节点n的概率为

其中

式中：τnm为时间 t时刻节点（n，m）上的信息素；a 为信息启发因子；b为期望启发因子；T为下一时刻可以选择的节点；ηnm（t）为时刻 t节点（n，m）上的能见度值；ynm*为当前最优路径节点纵坐标的大小。

假设，蚂蚁从一个节点爬到下一个节点的时间一样，与节点间距离无关，则所有蚂蚁爬到终点的时间是一致的。当时间等于15时，所有蚂蚁结束一次爬行，可以根据式（2）计算出 Kp，Ki，Kd值，利用所求得值对系统进行仿真分析。目标函数的建立需要根据系统的性能指标，选择式（6）绝对误差矩在时间t上的积累作为目标函数，反映系统快速性与实时性的指标，即

3.3 信息素的更新

蚂蚁经过的路径会遗留信息素，但是随着时间的推移，信息素也会消失，所以信息素是动态变化的。信息素的更新变化按式（7）进行变化，即

其中

式中：ρ为挥发系数，且 0＜ρ＜1；Δτ（xn，ynm，t）为节点c 在 t时刻信息素的变化总量；Δτk（xn，ynm，t）为 k 只蚂蚁爬过节点 c（xn，ynm）上信息素变化量；Fk为第 k只蚂蚁的目标函数值；Q为蚂蚁完成一次探索释放信息素总量，为一个常数。

3.4 算法实现的步骤

步骤1设定初始参数，蚂蚁数量m只，将蚂蚁放置在原点处；

步骤2按照式（3）计算出各节点转移概率P，并且记录蚂蚁下一个可能爬行的节点；

步骤3当蚁群完成一次迭代后，计算出相应Kp，Ki，Kd及性能指标，并赋值给 PID 控制器，系统运行得到目标函数，记录本次结果；

步骤4按式（6）更新信息素，增加一次迭代次数，判断是否达到最大迭代次数，如果达到就退出；否则，进入下一个循环直至达到最大迭代次数NC，输出最优PID参数。算法流程如图7所示。

图7 蚁群算法流程Fig.7 Ant colony algorithm flow chart

4 MatLab/Simulink仿真与试验分析

为了使得Kp，Ki，Kd可快速收敛，限定其范围，下限为（3.4，0.67，0.85），上限为（6.53，11.5，15.6）。初始化选择蚂蚁数量 M＝10 只，取 ρ＝0.5，a＝0.4，NC＝20，选取被控对象为一阶惯性1/（8s+1）。为了比较蚁群算法ACO-PID与经典PID参数整定性能，在MatLab/Simulink中建立仿真模型如图8所示，仿真结果如图9所示，性能指标见表1。

图8 PID Simulink仿真模型Fig.8 PID simulink simulation model

图9 仿真及试验波形Fig.9 Simulation and test waveform

表1 仿真结果性能指标Tab.1 Simulation result performance index

图9a，b中，信号选取单位阶跃信号，性能指标选取上升时间tr，调节时间ts，超调量γ，启动MatLab中m文件调用PID仿真系统，PID参数经过蚁群算法优化得到仿真图形。图9a中PID参数根据经典PID的 Z-N 法 Kp，Ki，Kd分 别为 3.4344，6.7675，8.5336。图9b中PID参数基于蚁群算法整定的最优Kp，Ki，Kd分别为 6.5254，1.2121，0.8534。

PID与ACO-PID试验采集到的对比波形如图9c所示。按照上述方法将PID参数设定在一定范围得到图 9c，PID 参数选取较大数，下限为（10000，10，5），上限为（50000，100，20），进行蚁群寻优。经过 MatLab运行蚁群算法程序得到PID参数最优值Kp，Ki，Kd分别为 48622，86.6，18.5。

由表1可知，ACO-PID的超调量和调节时间明显优于PID控制，图9c波形为 PID与基于蚁群优化PID试验波形的对比。试验给定脉冲峰值电流280 A，峰值时间2 ms，脉冲基值电流 45 A，基值时间4 ms，ACO-PID控制波形比PID控制波形更稳定。

对3 mm厚的铝合金板材进行焊接试验，焊缝形貌如图10所示。试验参数选取如下：单脉冲MIG焊，频率为83 Hz，焊接电流为110 A，焊接电压为22 V，焊接速度为43 cm/min，选取3 mm厚的AA6061-T6铝合金，采用直径1.2 mm的ER4043焊丝，保护气体为体积分数99.9%的高纯Ar气。试验结果表明：焊缝的余高和熔宽基本没有变化，飞溅少，焊缝成形质量高。结果证明，基于蚁群算法的PID参数自整定控制，在脉冲MIG电流波形控制中具有可行性。

图10 焊缝形貌Fig.10 Weld appearance

5 结语

基于蚁群算法的PID参数自整定具有良好的鲁棒性和自适应性，能够快速搜索到合理有效的PID参数，结合对焊接脉冲电流的控制，能够高效整定出合理参数，使得MIG焊脉冲电流快速收敛，提高稳定性。该算法对PID参数整定具有快速响应、调节时间比较短、超调量较小的特点，与经典PID控制相比，可以获得更有效、准确的整定PID参数。仿真和试验结果表明，蚁群算法在MIG焊脉冲电流PID参数优化中具有可行性。