神经网络软测量在家用房间空调器制冷量测量中的研究与应用

翁俊杰

（威凯检测技术有限公司 广州 510000）

引言

随着科技的不断进步，人工智能已经逐渐应用到社会分工的各个领域，在现代检测检验活动中的应用也越来越广泛。采用人工神经网络的软测量技术对家用房间空调器制冷量进行测量为这一领域的技术发展提供了一种新的思路和方向。

1 家用房间空调器系统软测量物理模型构建

根据国家标准GB/T 17758-2010中对于空调器制冷量测试的要求，测量家用房间空调器制冷量可以采用多种方法，其中采用室内侧空气焓差法和制冷剂流量计法都是针对空调器室内侧状态参数进行测量的方法，其区别如表1所示。

表1 制冷量测试方法差异表

而室内侧空气焓差法因其具有测试设备投入较少，设备维护方便，测量过程时间较短等特点，被行业中多数企业和检测机构所采用。这种方法主要是通过测定空调室内机进风口、出风口的空气焓值，以及空气流量确定制冷量的。空气焓值又是通过测定空气干球温度、湿球温度计算得出的。制冷量φtci按以下公式计算[1]。

采用制冷剂流量计法测量空调系统制冷量，φtci制冷量是通过测定室内侧热交换器中的进口制冷剂焓值、出口制冷剂焓值、以及制冷剂流量确定的。

通常把焓表示为以下公式

式中，u为内能，

所以工质的焓值可以由对应的温度和压力得到[2]。表达式如下：

在采用制冷剂流量计法进行测量的时候，由于进行检测的空调器多数都是成品机，在空调系统中接入流量计和压力表测量制冷剂流量和压力将破坏其原有系统，所以直接测得其制冷剂流量和压力难以实现。

通过对空调系统及其组件进行分析可以知道，空调系统由四大关键组件构成，分别为压缩机、蒸发器、冷凝器、节流装置，普通家用房间空调器多为一拖一空调系统，其系统示意图如图1和图2所示。

根据标准CAN/ANSI/AHRI 540，压缩机制冷剂流量可以表示为以下公式[3]：

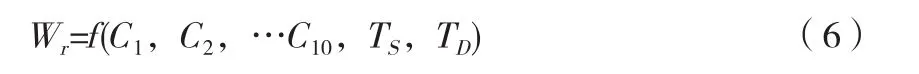
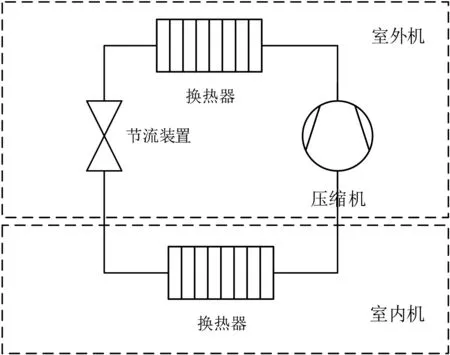
图1 一拖一单冷式空调系统

图2 一拖一冷暖式空调系统

即压缩机中制冷剂流量可以由C1～C10十个系数以及吸气口温度TS和排气口温度表示TD，C1～C10十个系数与压缩机转速n有关。

空调器室内侧换热器在进行制冷运行时其作用为蒸发器，由于标准中要求，测量需在各参数稳定时进行，所以蒸发器采用稳态集中参数模型[4]进行分析，稳态集中参数模型忽略了蒸发器内的流动压降而不考虑动量方程，稳定的流动使制冷剂质量方程也得到满足，因此模型只需要考虑空气侧流动换热和制冷剂侧流动换热的能量方程[5]。

对于蒸发器制冷剂侧，有流动换热方程：

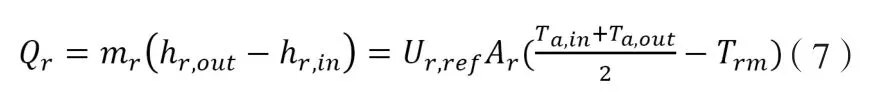
为了提高蒸发器过热度的仿真精度，采用过热区换热量加倍的改进方法，同时为保证计算迭代的收敛性，制冷剂平均定性温度Trm取制冷剂进口温度hr，in。

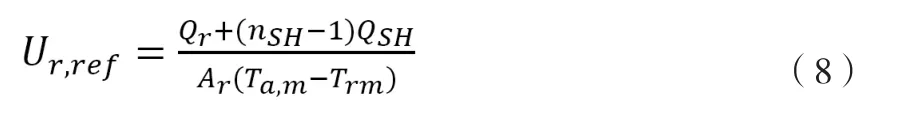
过热区换热量QSH为：

当nSH=1时就退化为传统定义。

所以公式3可以转化为：

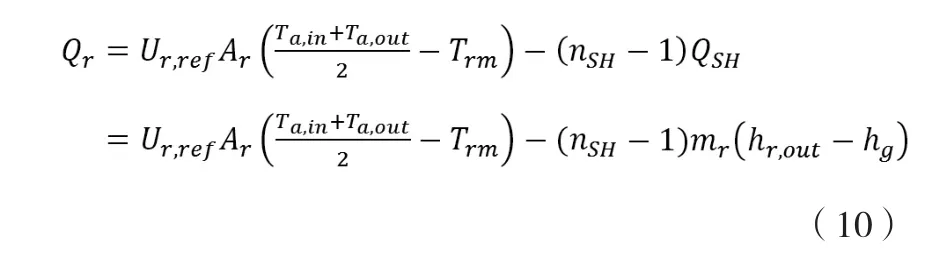
目前，对于一拖一家用空调系统而言各生产制造企业一般将蒸发器饱和气体点设计在蒸发器中间处，蒸发器中间处制冷剂焓值用表示hg，温度用表示Tg，压力用pg表示。

由于制冷剂相变过程具有下述特点：在一定压力下，过程中物质的温度保持不变，反之亦然。此时饱和温度与饱和压力间存在如下一一对应的关系[6]：

Tg=f(pg)或pg=f(Tg)

所以，

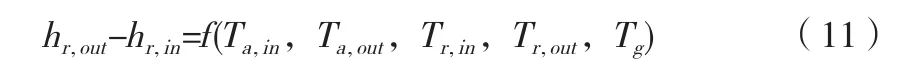
综上所述，采用制冷剂流量计法进行测量的时候，公式2制冷量φtci可以表示为：

2 BP神经网络设计

空调系统是多组件构成的系统，各组件的热力学结构复杂，组成的系统具有高度耦合性，采用BP神经网络结合热力学原理进行建模将是一个较好的选择。BP神经网络具有较强的学习能力，通过对非线性单元的复合映射，可获得复杂的非线性处理能力，常用于预测回归、分类、模式识别等。

BP神经网络是一个多层神经网络，从结构上讲，其具有输入层、隐含层和输出层，其中输入层和输出层为单层网络，隐含层可以由单层网络构成，也可以由多层网络构成。每一层网络间进行全连接，而同一层网络中的神经元无连接。BP神经网络也称为误差反向传播神经网络。基本BP算法(Error Back Propagation Training)包括两个过程：信号的正向传播和误差的反向传播，即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传沿原来的连接通路返回，将输出误差通过隐含层向输入层逐层反传，通过修改各层所有神经元的权值，以从各层获得的误差信号作为调整各单元权值的依据，使得误差信号最小。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止[7]。

BP神经网络在设计时，隐含层一般使用S型（Sigmoid）函数作为激发函数，输出层则采用线性函数。S函数又可分为Log-Sigmoid和Tan-Sigmoid函数。

采用Log-Sigmoid函数时，可记作：

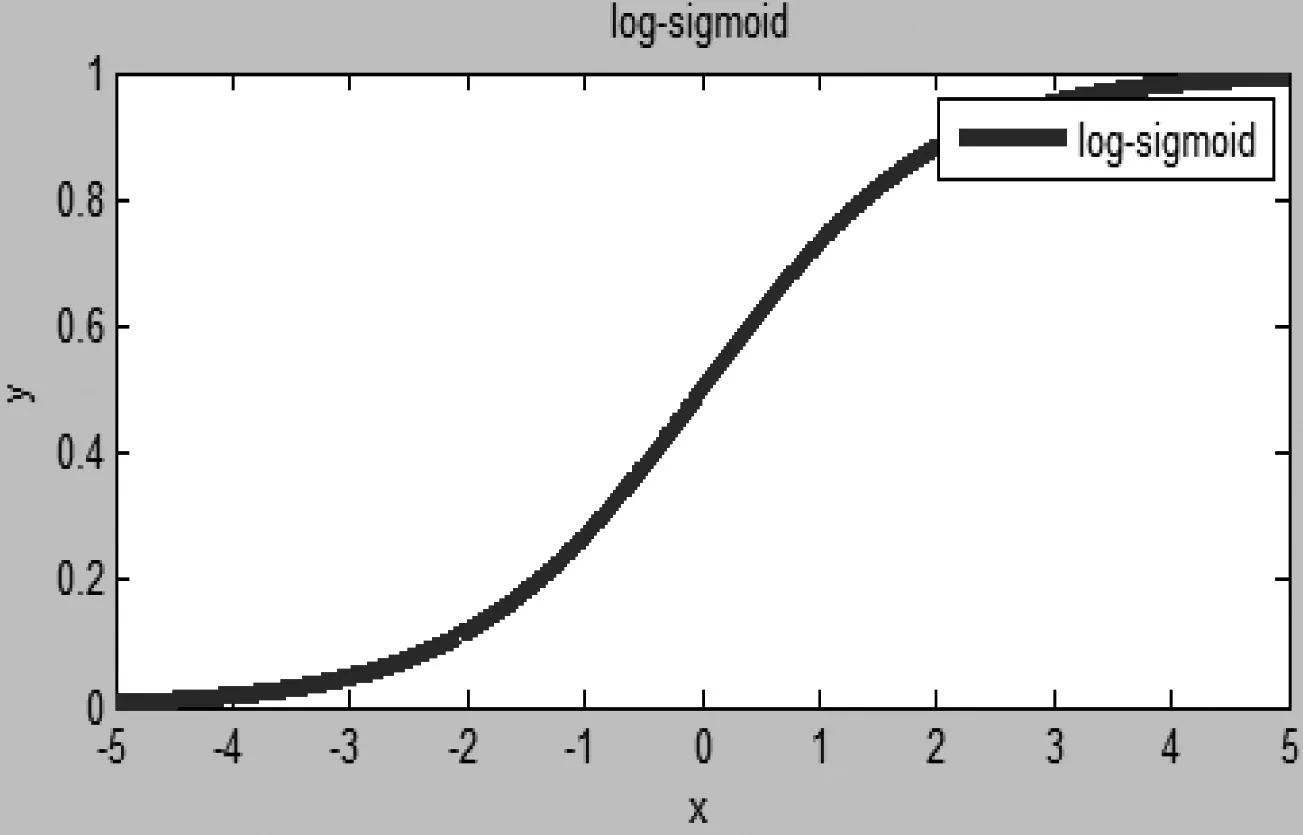
图3 log-sigmoid函数

图4 tan-sigmoid函数

图5 BP神经网络设计流程图

当β趋于无穷时，S型曲线趋于阶跃数，通常情况下，β取值为1。

使用S型函数时，它能够将输入从负无穷到正无穷的范围映射到输出为（0，1）或（-1，1）区间内，是在区间内连续取值的单调可微函数，

BP神经网络设计流程如图 5。

一个设计合理的BP神经网络具有能够拟合任一非线性函数的特点，所以依照上述物理模型φtci=f(n，TS，TD，Ta，in，Ta，out，Tr，in，Tr，out，Tg) 设计 B P 神经网络有 8个输入参数，一个输出参数。BP神经网络采用三层结构即输入层、隐含层、输出层，其中输入层有8个神经元节点，输出层有一个神经元节点，隐含层节点数量按照经验公式：

其中S为隐含层神经元节点数量，n为输入层神经元节点数量，m为输出层神经元节点数量，a可以取0～10间的常数。所以可以设计隐含层神经元节点S数量为5。综上所述，BP神经网络结构可以设计为8-5-1。

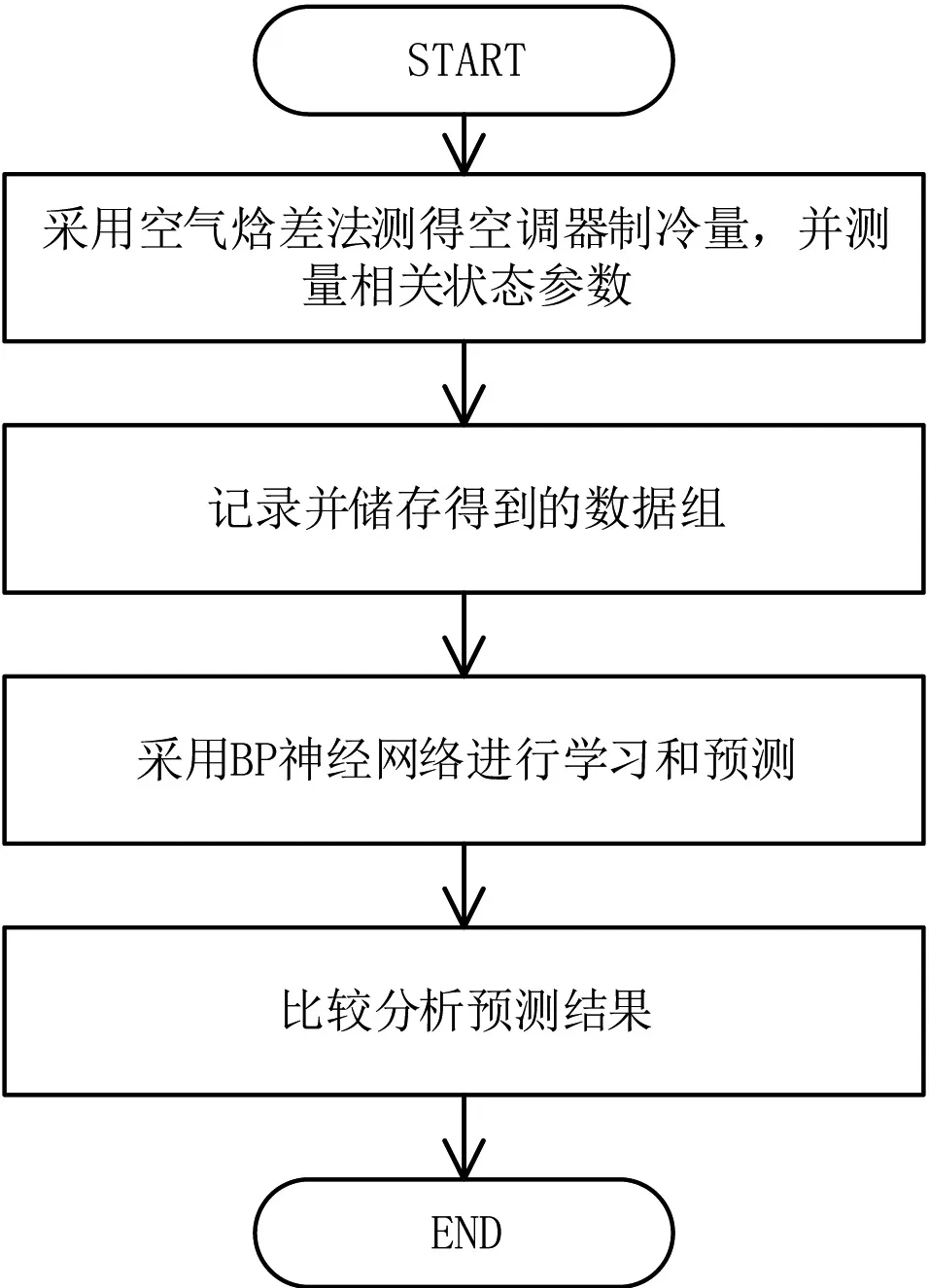
图6 软测量设计思路流程图

3 软测量的实现

根据之前论述，对家用房间空调系统制冷量采用软测量的方法进行测量，整体设计思路如图6所示。

抽取一套普通家用房间空调器进行测量，空调器铭牌参数摘录如表2所示。

采用空气焓差法获得空调系统不同工况下的制冷量、室内侧进、出风口干球温度、湿球温度，以及采用J型热电隅紧贴管壁，近似获得空调系统中压缩机制冷剂吸气口温度、压缩机制冷剂排气口温度、蒸发器进口制冷剂温度、蒸发器出口制冷剂温度、蒸发器管路中间制冷剂温度。记录并存储后得到50组数据。从50组数据中随机抽取40组数据作为训练数据训练神经网络，10组数据作为网络测试数据，用训练好的神经网络对空调系统的制冷量进行软测量。采用MATLAB软件对BP神经网络进行仿真后，训练效果如图7-9所示。

制冷量预测结果与实测结果比较如图10所示。

软测量得到的制冷量和实际制冷量误差如图11所示。

软测量得到的制冷量和实际制冷量误差百分比如图12所示。

表2 被测空调器铭牌参数摘录表

图7 BP神经网络训练效果图

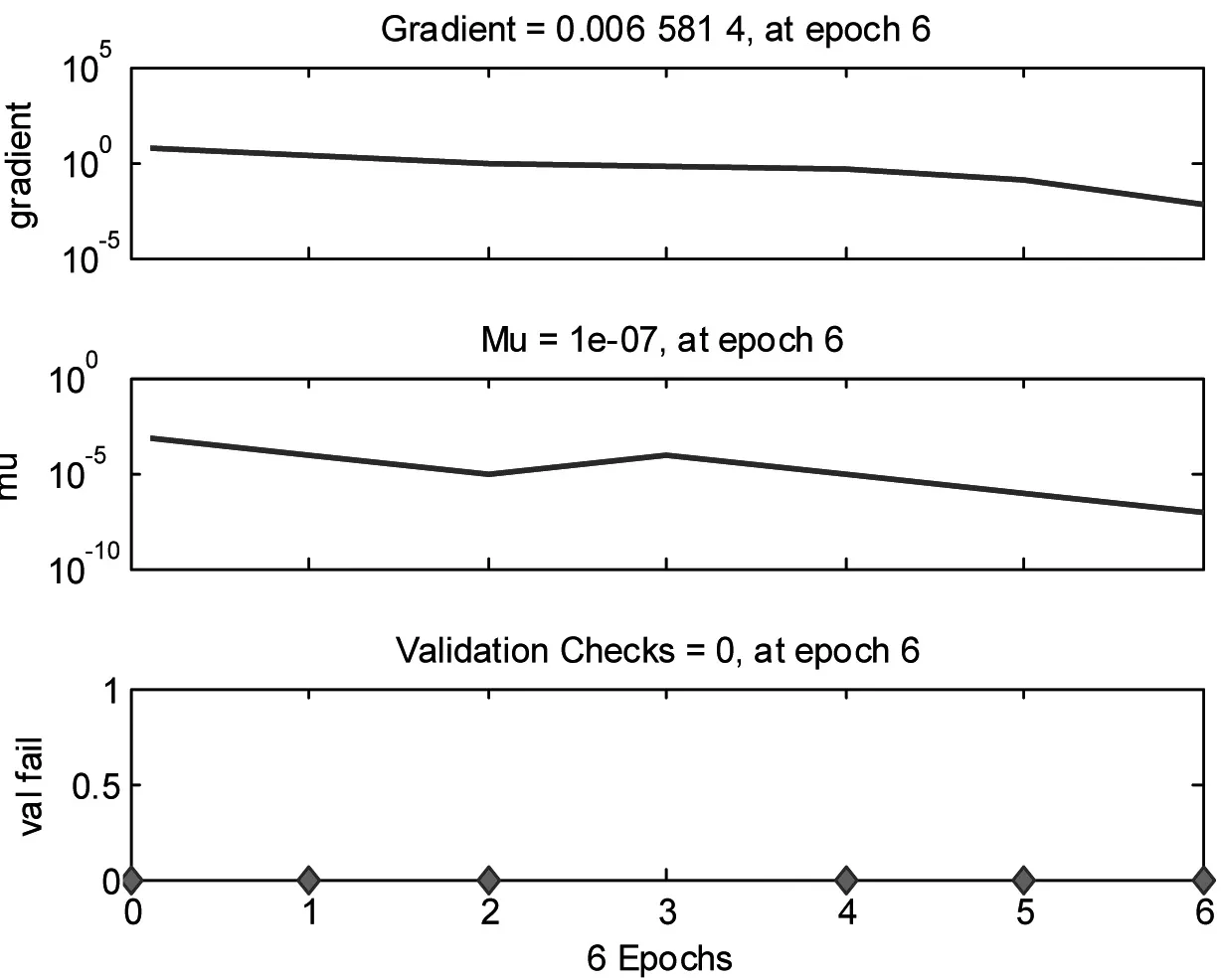
图8 BP神经网络训练效果图

图9 BP神经网络训练效果图

图10 BP神经网络预测结果与实测结果对比图

仿真结果表明，采用BP神经网络进行软测量，其预测结果与实测结果具体情况如表3所示。

其中最大误差百分比为2.44 %。

根据空调系统制冷量表达式，其中影响制冷量的状态参数较多，然而哪个参数对制冷量的影响更大却无法确定。针对这一问题，本文采用平均影响值MIV(mean impact value)对BP神经网络输入节点中的状态参数重要性进行筛选。MIV是判断输入变量对输出变量影响权重的较好指标之一，其符号代表相关方向，绝对值大小代表影响的相对重要性[8]。MIV方法的具体实现过程如图13所示。

经过采用MATLAB对BP神经网络各输入节点重要性进行筛选之后，得到以下MIV数值，如表4所示。

图11 BP神经网络预测误差

图12 BP神经网络预测误差百分比

4 结论

采用BP神经网络对空调系统制冷量进行软测量的结果表明，采用BP神经网络对空调系统制冷量进行软测量能够达到较好的效果，测量误差在可接受的范围之内。并且通过MIV平均影响值对BP神经网络各输入节点重要性进行筛选之后的结果表明，压缩机频率、排气侧压力等状态参数对制冷量预测结果的影响较其它参数更大，此结果与压缩机在系统中的重要性常被喻为空调系统的“心脏”是较为一致的。同时从仿真的结果也发现，由于采用的数据组数量较小，影响了软测量的效果，在后期研究中将采取措施进行改进。

表3 BP神经网络预测结果与实测结果具体情况

表4 BP神经网络各输入节点MIV数值

图13 MIV方法对BP神经网络进行变量筛选流程图