云环境下基于线性回归算法的PM10—能见度—湿度相关性研究

李 敏, 程茂华, 潘 颖, 李 雄

(1.南宁师范大学 计算机与信息工程学院，广西 南宁 530023;2.广西科技师范学院，广西 来宾 546199;3.广西气象台，广西 南宁 530022)

在目前的研究中，经常使用数学领域中的统计学方法对湿度、大气能见度与气溶胶PM10进行研究，分析显示PM10浓度增大以及颗粒物吸湿性增长可导致能见度数值降低[1]。但总体而言，当下仍缺乏湿度、大气能见度与气溶胶PM10存在何种相关性的研究。

此外，气象领域在处理气象数据的问题上使用的多是投入耗费大的传统方法。云计算的低成本运算快成为了出来当前大数据的热门途径，但需要适当的处理体系结构与密集任务的协调性。因此挑选合适的机器学习算法可以高效率地处理与分析大规模的数据。并行性以及运算效率是大数据计算需要攻克的难题。

本文基于中国气象局气象数据中心和南宁市环保局环境监测站历年气象数据。设计云环境下DMLR(Distributed Multiple Linear Regression)模型用于能见度、湿度与气溶胶PM10相关性的研究，实验分析表明，湿度区间一致大气气溶胶PM10浓度越大能见度就越小，能见度区间一致大气气溶胶PM10浓度越低湿度越大。实验结果还发现湿度介于40%-90%，能见度介于8km-19kmDMLR预测效果最好。

1 相关研究现状

1.1 机器学习算法的研究现状

国内外人员提出了各种分布式数据分析方法以解决传统的数据挖掘计算及保存能力不够的问题。宋欣、王翠荣[2]提出回归模型的参数信息代替实际感知数据的线性回归分析方法构建感知数据模型，仿真实验结果表明，文中提出的数据采集优化策略能通过较小的通信量有效地实现事件监测区域感知数据的预测，降低网络的总能耗，延长网络的生命周期。付倩娆[3]提出一种在线样本更新的多元线性回归的雾霾预测方法，通过在线样本更新的多元线性回归建立了PM2.5含量预测模型,并将气象要素作为雾霾的判断标准。实验结果证明提出的方法对一周以内的PM2.5含量预测准确率较高。戴李杰[4]等提出基于机器学习的PM2.5短期浓度动态预报模型，联合应用支持向量机(SVM)和粒子群优化(PSO)算法建立滚动预报模型,对PM2.5未来24小时浓度进行预报,同时对未来一天的昼、夜均值及日均值浓度进行预报,并与径向基函数神经网络(RBFNN)、多元线性回归法(MLR)、模式预报(WRF-Chem)作对比。实验表明,所提出的SVM模型较其他方法提高了PM2.5未来1小时浓度预报精度；所提模型能对PM2.5未来24小时浓度进行较好的预报,能对未来一天的昼均值、夜均值及日均值进行有效预报,并且对未来12小时的逐时浓度及未来一天的夜均值浓度的预报准确度较高。

1.2 能见度、湿度与PM10的相关性研究

国外已有针对空气中PM10浓度问题的相关性研究。Song Liu等人[5]提出基于MODIS数据估算的能见度和相对湿度检测雾霾及其强度。实验表明在这两个指数中，能见度在影响检测精度方面比相对湿度起着更重要的作用。Nan Ma[6]等人提出一种新的基于PM2.5，能见度和相对湿度区分雾和雾霾的方法，基于雾霾与雾的物理性质的差异，本研究提出了一种利用PM2.5，能见度和相对湿度的实时测量来区分雾霾和雾的新方法。在该方法中，可以基于粒子数量大小分布和气溶胶吸湿性的局部历史数据来建立标准。根据该标准可区分雾和雾霾。我国在1970年开始，也对空气中的颗粒物进行大量的研究，董继元等[7]对兰州市大气相对湿度与PM10浓度和大气能见度进行相关性分析，利用兰州2002—2012年的环境气象资料,对相对湿度RH、PM10浓度与能见度之间的对应关系进行统计分析,以揭示RH与PM10浓度和大气能见度之间的直观联系,加深对灰霾形成过程的认识。该研究表明:PM10平均值与RH平均值表现为负相关，相对湿度较高时大气颗粒物含量较高。刘凡等[8]分析了成都市冬季相对湿度对颗粒物浓度和大气能见度的影响，利用2015年12月的连续在线观测数据，探讨RH对颗粒物浓度和大气能见度的影响。结果表明，高颗粒物浓度和高RH协同作用导致低能见度事件。随着RH增加，PM2.5∕PM10显著增加，表明高RH会加重细颗粒物污染。随着PM2.5浓度增加，能见度呈幂指数下降；在相同PM2.5浓度下，RH越高，能见度越低。基于上述研究，探讨南宁区域的气溶胶与能见度、湿度之间的相关性意义重大。但目前对气溶胶PM10、能见度以及湿度的研究只是简单、定性的统计分析，不能很好地反映他们之间的相关性。

2 DMLR线性回归模型

2.1 线性回归

建模的思想在处理大数据分析的研究中作用很大。线性回归是其中较为经典的建模形式，其表达形式为y=w′x+e，e为误差服从均值为0的正态分布。线性回归中只有一个回归变量和一个依赖变量，称为一元线性回归[9]。线性回归中有两个以上的回归变量，且回归变量之间存在线性关性，则称为多重线性回归[9]。多重线性回归方程：

y=β0+β1X1+β2X2+…+βj-1Xp-1+ε

(1)

上式子中y表示因变量；Xp是自变量，p=1，2，3，…，p-1；βj是y基于每个Xp单元变化的变化量，j=1，2，3，…，j-1；残差ε。本文使用最小二乘逼近来拟合模型。式(2)是对样本数据集(xi1，xi2，xi3，…，xi(p-1)，yi)的回归模型：

(2)

矩阵表示：

(3)

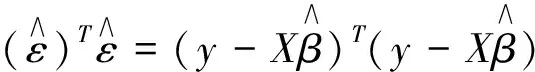
(4)

2.2 DMLR模型设计思想

(5)

采取划分模块将输入样本在云平台多个集群上运算以达到并行加速效果。并行化设计中各特征上的梯度元素进行累加：

(6)

(1)导入训练集、测试集并设置迭代轮数100以及更新步长A的值；

(2)将训练集分块到B个计算节点；

(3)对每一个计算节点采样计算损失值LB与梯度LB，并对分片目标向量更新即LB；

(5)迭代运行步骤(3)、(4)至目标值收敛；

(6)将测试数据集预测结果输入到评估模型评估。

本文在云环境下面向PM10—能见度—湿度相关性的研究提出DMLR模型。DMLR线性回归模型数据集训练实验流程如图1：读取实验数据集并对数据直方图统计、全表统计和拆分操作；本文实验将拆分参数设置为0.7，70%作训练集，30%作测试集。然后使用DMLR模型对输入的训练集进行训练并结合测试集预测，最后使用评估模型来评估线性回归模型的预测准确程度以及气溶胶PM10浓度的变化与湿度、大气能见度的相关性。

图1 DMLR模型实验流程

3 DMLR模型实验结果与分析

3.1 实验数据集

实验过程中使用广西南宁环保局环境监测站以及中国气象局气象数据中心历年气象数据，气溶胶PM10为1989—2017年数据；能见度为1980—2017年数据；湿度为1980—2017年数据。

实验将湿度、能见度各划分三个等级如表1所示：

表1 湿度、能见度等级划分表

然后对这六个区间等级进行两两组合构成共9个实验数据源，其中数据源2的部分数据如表2所示。

3.2 实验结果及分析

按照图1的DMLR模型实验流程对以上数据表进行预测分析，表3为数据表2(湿度值<40%，8km<=能见度值<=19km组合)的DMLR模型的PM10预测结果，表4为回归模型评估结果。

表2 数据源2部分数据

表4 数据源2评估结果

R表示多重相关系数，R2表示判定系数，RMSE表示均方根误差，SSE表示误差平方和；SSR表示回归平方和，SST表示总平方和，yMean表示原始因变量均值，prediction Mean表示预测值的平均值。

根据上文的9种组合方式各数据源的实验分析结果如表5所示：

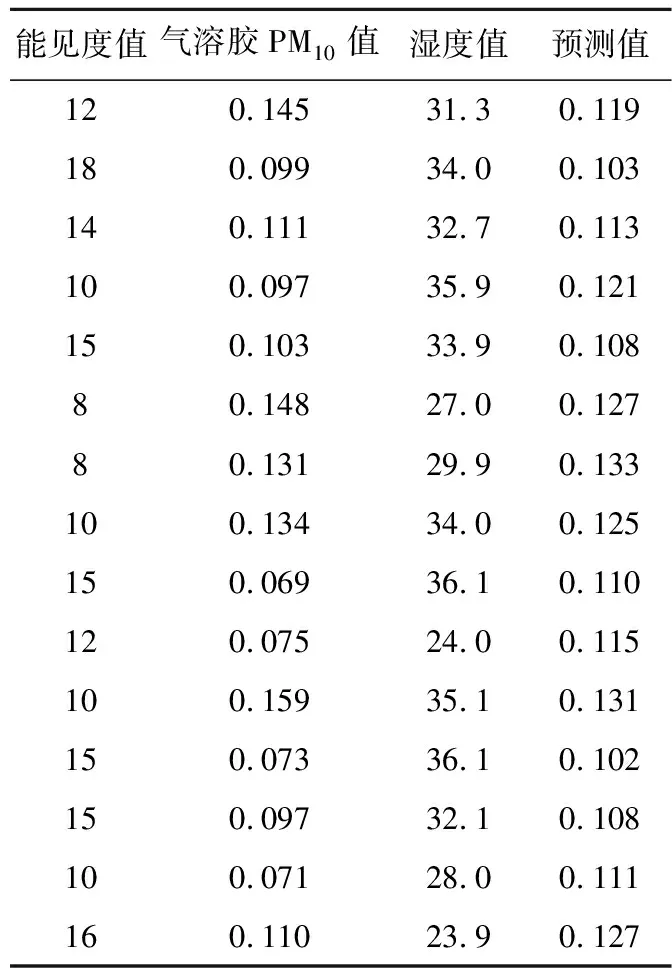
表3 数据表2DMLR模型的PM10预测结果

表5 湿度、能见度等级划分表

图2 数据源2预测值与原值拟合图

置信概率(confidence probability)是用来衡量统计推断可靠程度的概率。其意义是指在进行统计推断时.被估参数包含在某一范围内的概率；本文显著性阈值设置为95%。实验证明数据源2、数据源3、数据源7、数据源8、数据源9显著性较强，置信率高；数据源1、4、6的实验数据限制于满足本文设置提取的实验数据量太少，实验结果显著性较低，置信率低。下文给出了数据源2、7、8的实验预测值与实验数据原值的拟合图及相对应的DMLR模型输出结果。

实验结果表明湿度在40%-90%、能见度在8km-19km区间范围内预测效果最优，湿度小于40%、能见度在8km-19km区间范围内预测效果偏差。实验得出结论以下结论：

表6 数据源2DMLR模型输出结果

表7 数据源7DMLR模型输出结果

表8 数据源8DMLR模型结果输出

1.在同一湿度区间内，能见度与PM10呈负相关，即能见度越小PM10浓度就越大。

2.在同一能见度区间内，湿度与PM10呈负相关，即湿度值越大PM10浓度就越低。

图3 数据源7预测值与原值拟合图

图4 数据源8预测值与原值拟合图

另外实验结果表明PM10浓度与能见度、湿度的相关系数，能见度的相关系数更高。集合实验结果分析三者之间的关系如图5所示。

3.3 DMLR模型和传统回归模型时间性能的比较

比较DMLR算法模型与传统回归模型实验运行时间(图6)。在数据表2、5、7、9中，DMLR算法模型运行时间明显少于传统回归模型，其减少幅度为10%；而在表1、3、4、6、8中，DMLR算法模型和传统回归模型实验运行时间相同。总体而言，DMLR算法模型在时间性能方面要优于传统回归模型。

图5 PM10—能见度—湿度相关图

图6 DMLR模型与传统回归模型运行时间

4 结 论

本文提出一个基于云平台的DMLR机器学习模型，分析以湿度值和能见度值作为自变量，PM10气溶胶值作为因变量的相关性。实验结果发现湿度介于40%-90%，能见度介于8km-19kmDMLR预测效果最好，DMLR算法模型在时间性能方面要优于传统回归模型。此外，在云环境下对能见度、湿度与PM10的相关性提出DMLR模型，在可行性方面得到了验证，具有一定的应用意义。

我们的工作存在如下不足：在未来的研究中需要解决的问题，如实验气象因子(如风速、降水等)需加强；区域不同是否对气溶胶与能见度、湿度之间的相关性影响并未加入考量。