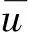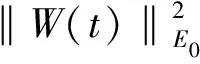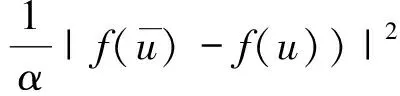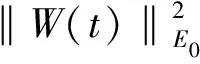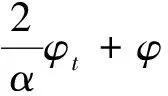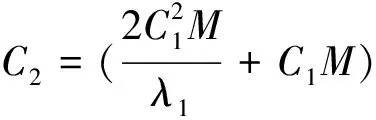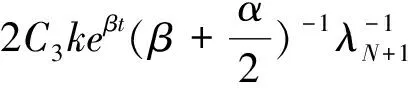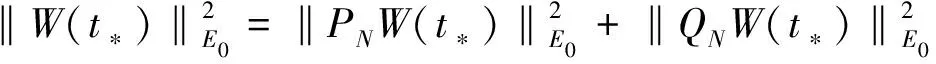Plate方程指数吸引子的存在性
2019-09-02苏小虎姜金平
苏小虎, 姜金平
(延安大学 数学与计算机科学学院,陕西 延安 716000)
我们考虑如下plate方程
(1)
指数吸引子的存在性,其中:Ω⊂Rn是光滑边界上的有界区域;u=u(x,t)是Ω×(τ,+)上的未知函数;α>0为粘性阻尼;g∈L2(Ω);ε(t)∈C1(R)是有界的单调递减函数,并且满足

假设非线性函数f∈C2(R,R)满足下面条件:存在C0>0,使得:对∀s∈R,有

Plate方程来源于弹性振动方程,近几年对Plate方程吸引子的存在性问题研究十分广泛。有许多学者在不同方向做了研究,文献[1,2]研究了有界域上Plate方程一致吸引子的存在性;文献[3-5]主要研究了在无界区域上Plate方程全局吸引子的存在性;文献[8-9]分别研究了Plate方程时间依赖全局吸引子的存在性和非自制Plate方程时间依赖强拉回吸引子的存在性,马巧珍等人[11,12]对梁方程进行了研究,证明了梁方程指数吸引子及全局吸引子的存在性。受文献[5-9]的启发,本文证明了Plate方程在相空间E0上指数吸引子的存在性。
1 预备知识
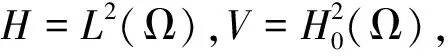
定义D(A)={v∈V,Av∈H}|,其中Av=Δ2v,D(A)的内积和范数分别用(Au,Av)和|Au|2=(Au,Au)表示,显然,我们有D(A)⊂V⊂H=H*⊂V*,在这里嵌入都是连续的且其值域是稠密的,其中H*,V*分别表示H和V的对偶空间,记V*的范数为‖·‖V*。因为A是正对称算子,对任意的s∈R,定义V2s=D(AS)上的幂算子As,则内积内积和范数
另外,A是正定的,且有紧逆的自伴算子,若{ωn,n=1,2,…}是A的完备特征向量,则λ1,λ2,…为特征值,且满足
0<λ1λ2…λn…,λn→,n→。
根据Poincae不等式,有
‖v‖≥λ1|v|,∀v∈V。
(2)

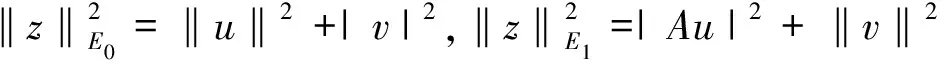
定义1.1[6]设{S(t)}t≥0是相空间E上的半群,紧集M⊂E被称为是({S(t)}t≥0,E)的指数吸引子,如果满足下列条件:
(i)S(t)M⊆M,∀t≥0;
(ii)M有有限分形维数,即dimFM<;
(iii)对E中的任意有界集B,存在常数a0,a1>0,使得对∀t≥0,成立
dist(S(t)B,M)a0exp(-a1t)。
根据指数吸引子的定义,若半群存在指数吸引子M,则全局吸引子A⊂M,且分形维数满足dimFA ‖(I-PN)(Su-Sv)‖E‖PN(Su-Sv)‖E 或者有 ‖(Su-Sv)‖Eδ‖u-v‖E 成立。 定义1.3[7]若B⊂E有界,{S(t)}t≥0是E上的半群,若存在t*>0,映射S*=S(t*)满足挤压性,则半群{S(t)}t≥0在B上满足离散的挤压性。 定理1.4[7](i)若ε,α>0,g∈Cb(R+;H),对于初值(u0,u1)∈E0,则方程(1)有唯一的解u(t),使得: 定理1.5[8]假设(H1)-(H2)中的条件成立,B0=BE0(0,ρ0)是(1)生成的解半群{S(t)}t≥0在E0中的有界吸收集,在这里空间E0以0为中心,ρ0为半径的球,则E0中的任意有界吸收集B,∃t0(B)>0,使得当t≥t0(B)时,有S(t)B⊂B0。 定理1.6[8]假设(H1)-(H2)中的条件成立,则(1)在E1中存在有界吸收集BE1(0,ρ1),有 B0={(u,v)∈V×H=E0:‖u‖2+|v|2 B1={(u,v)∈D(A)×V=E1:|Au|2+‖v‖2 B0和B1是E0,E1中的不变吸收集。其中定义B=B0∩B1作为E0的不变紧集,则在E0是紧的,在E1中是有界的,在B上定义半群{S(t)}t≥0,有S(t)B⊂B。 引理1.7设存在一个常数C,使得 其中z0=(u0,u1),z(t)=(u(t),ut(t))。 证明令ψ=ut,由方程(1)得 ε(t)ψtt+Δ2ψ+αψt+f′(u)ut=0, ψ(0)=u1, 据参考文献[10],我们得 用2ψt+2δψ做内积得 其中 Λ(t)=‖ψ‖2+ε(t)‖ψt‖2+δα‖ψ‖2+2δε(ψ,ψt) 利用Hölder与Young不等式 2δ|ε(ψt,ψ)| 其中|ε(t)|L,当这里的δ足够小时,存在 (-f′(u)ut,2ψt+2δψ)2‖f′(u)ut‖(‖ψt‖+δ‖ψ‖) 由Gronwall引理,可得 根据上面定义及定理,下面将依次来验证(1)中半群{S(t)}t≥0在E0中的Lipschitz连续性和挤压性。 为进一步证明,先引入 HN=linearspan{ω1,ω2,…,ωn} (3) pN:H→HN,qN=I-PN。 再由投影的定义,我们得到 |u|2 现在令 PN:E0→(pNV)×(pNH),QN=I-PN。 (4) 定义 PN(u,v)=(pNu,pNv),(u,v)∈E0。 (5) 为了方便证明,我们构造函数 N(z)=‖u‖2+|v|2+λ|u|2,∀z=(u,v)∈E0 (6) 和 引理1.8(i)由N(·)导出的范数等价于E0上的范数,即有 ‖u‖2N(z) (8) (ii)M(z)的范数等价于空间QNE0上的E0范数,取N0=max{N1,N2}足够大,使得 (9) 证明(i)对N(z)=‖u‖2+|v|2+λ|u|2,∀z=(u,v)∈E0, 由Poincaré不等式得 ‖u‖2+|v|2+λ|u|2 再者 (ii)由于z=(u,v)∈QNE0,u∈qNV。利用(1.4)得 又由于 (u,v)|u||v| 于是 即引理(1.8)得证。 通过上述定理及引理的证明,下面我们进一步探究在相空间E0上方程(1)是否满足Lipschitz连续及离散的挤压性条件。 (10) (ii)令φ=qNω和φ(φ,φt)=QNW。则对于任意的t≥0,M(φ(t))满足微分不等式 (11) 其中C1是与ρ0,ρ1有关的常数,C2是与λ1,α,C1有关,而与φ,W无关的常数。 证明由于ωt满足方程(1),即 (12) 此时,我们令 用ωt与(12)做内积,并且在Ω上积分得 (13) 整理得 (14) 由条件(H2),定理1.5,1.6及Sobolev嵌入定理,存在M>0使得 |f′(u)|LM,|f″(u)|LM。 于是有 (15) 由(1.7),(13)-(15)我们得 由Gronwall引理得 N(W(t))eβtN(W(0)) 由(1.7)范数等价性,即有 (ii)用qN作用于(12)得下面方程 (16) 即有 (17) 又由于φ,φt∈qNV,因此有 ‖φt‖V (18) (19) 由范数等价性,即有 (20) 结合(18)-(20) (21) 因此,由上述引理有 (22) 引理2.2对任意的T>0,映射(t,u0)S(t)u0:[0,t*]×B→B是Lipschitz连续的。 证明对u0,u1∈B,t1,t2∈[0,T],有 ‖S(t1)u0-S(t2)u1‖E0‖S(t1)u0-S(t1)u1‖E0+‖S(t1)u1-S(t2)u1‖E0。 (23) 由引理1.7得 ‖S(t1)u0-S(t2)u1‖E0=‖u(t1)-u(t2)‖E0‖ut(y)dy‖E0C|t1-t2|。 因此 ‖S(t1)u0-S(t2)u1‖E0L[|t1-t2|+‖u0-u1‖E0]。 (24) 定理2.3选取t*,N=max{N0,N1,N2},满足 (25) 和 (26) 则E0中的有界子集B上的解算子{S(t)}t≥0满足Lipschitz连续和离散的挤压性。如果 ‖pNW(t*)‖E0‖QNW(t*)‖E0 则 证明对(22)运用Gronwall引理,得 M(φ(t)) 由(25)和(26)有 由上述定理得到解半群S*=S(t*)在E0中离散的指数吸引子M* 定理2.4在方程(1)中,设{S(t)}t≥0是相空间E上的半群,如果半群{S(t)}t≥0在非空紧正不变集合B⊂E0中满足离散的挤压性,则映射S*=S(t*)生成的离散动力系统存在一个指数吸引子M*若映射(t,u0)S(t)u0:[0,t*]×B→B是Lipschitz连续映射,则集合是{S(t)}t≥0在E0中的指数吸引子。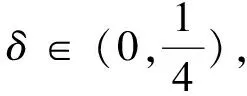
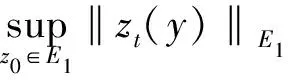




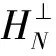


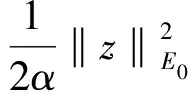
2 E0中指数吸引子的存在性