深水浊积水道训练图像建立与多点地质统计建模应用

2019-09-02尹艳树冯文杰王立鑫段太忠张文彪

石油与天然气地质 2019年5期

胡迅，尹艳树，冯文杰，王立鑫，段太忠，赵磊，张文彪

(1.长江大学，湖北武汉 430100; 2.中国石化石油勘探开发研究院,北京 100083)

随着人们将目光投向深水区，深水油气开发已经成为了油气增储上产的热点。深水水道是深水区重要的地形单元，其为连接陆架和深海平原的重要通道，是深水油气主要富集区，规模大，储层质量好[1-4]。深水水道主要为沉积物重力流沉积，流体性质复杂，以悬浮式搬运为主，沉积机制复杂。近些年，很多学者对深水浊积水道储层沉积特征与叠置样式进行了解剖，已取得一系列成果。浊积水道主要从单一水道、复合水道以及浊积水道体系3个构型单元分层次展开研究。单一浊积水道是深水水道的基本组成单元。单一水道间存在着反复切割与充填，可形成各种叠置样式的复合水道。同样，复合水道间也存在着切割与充填，最终形成浊积水道体系[5-9]。对于浊积水道空间分布的三维建模，目前也是一个研究热点。卜范青等采用分区法随机建模(基于目标的序贯指示模拟方法)，用来模拟不同物源，且无交叉叠合的两套沉积体系，接着采用水道趋势线法(序贯高斯模拟算法)模拟同一类沉积体系下的高弯度深水浊积水道[10]；张文彪等用基于目标的方法模拟深水水道，其中水道参数由“浅层类比”获得，完善了深水水道定量分布模式[11]；进一步的，张文彪等通过高精度梯度阻抗反演，提取浅层水道目标地质体作为深水水道定量化三维训练图像，采用多点统计Snesim算法进行随机模拟[12]，取得了较好的应用效果；针对水道构型解剖级次性，张文彪等采用多级建模的方法，水道级别模拟主要采用基于目标的模拟方法，水道内部构型则采用截断高斯模拟方法模拟[13]。

尽管浊积水道建模方法较多，如基于两点变差函数建模、基于目标建模、基于沉积过程建模以及多点地质统计随机建模方法等等。但两点统计学只能表达空间上两点之间的变化性，而不足以体现浊积水道储层非均质的复杂性；基于目标如布尔模拟方法对目标描述过于简单，浊积水道的平面摆动模式、垂向加积等现象无法体现；基于沉积过程建模在多井情况下的井数据条件化依然是个难题；多点地质统计学一定程度上综合了两点建模与目标建模优点，更好的再现了储层分布特征，但其训练图像获得具有较大的挑战性[14-20]。虽然可以依赖于高分辨率地震资料反演获得训练图像，但是其所获得的训练图像是确定的，而地震资料本身存在多解性，因此确定的训练图像难以体现储层变化性；此外，地震高分辨率往往存在于浅层区，而油气分布深层区地震品质相对差；浅层地震资料类比需要有充分依据，如果地震资料品质不好，则导致训练图像难以获得。因此，有必要围绕深层浊积水道训练图像自动建立开展研究，并服务于深水浊积水道建模。笔者围绕深水浊积水道训练图像难以准确获得这一难题，对基于沉积过程的Alluvsim方法进行了分析和改进[21]，使其适用于再现浊积水道演化的过程，重构浊积水道规模和叠置样式，形成浊积水道训练图像，服务于实际区多点地质统计学建模。通过安哥拉深水水道建模实例，给出了建模流程；通过对比建立的模型变差函数与地震属性变差函数差异，证实了建立的模型具有较高的可信度。本研究不仅为多点地质统计应用于实际储层建模提供了完整的建模流程，也为浊积水道训练图像自动生成提供了技术方法。

1 Alluvsim算法原理

Alluvsim算法是Pyrcz等提出的基于沉积过程的河流相随机建模方法，该方法通过河道中线操作可模拟河道的侧向迁移、垂向加积、分汊改道和决口等过程，并用几何形态参数对河道中线上所有的节点赋值，建立每期河道的三维构型模型，最终实现曲流河模拟[21-24]。该算法建模步骤为：

① 产生初始河道中线。根据已有地质知识库，产生一个候选河道中线库，根据河道水平趋势分布规律随机地选择一条河道中线。其中河道中线生成采用的是Ferguson提出的周期性扰动模型，具体是根据初始节点位置，步长，初始曲率，主河道方向来产生[25]。

② 根据几何形态参数对河道中线上所有节点赋值，建立该条河道的三维构型模型。

③ 判断是否发生截弯取直。该过程通过比较不相连的节点间距和河道宽度大小来实现，如果不相邻节点间距小于河宽，则发生颈切，形成废弃河道。

④ 产生下一条河道。根据概率值进行河道中线操作，包括产生新河道、河道分叉和河道侧向迁移。产生新河道是在河道中线库中随机选择；河流改道中分叉位置根据曲率大小决定，曲率大的位置发生分叉概率大，分叉节点后根据周期扰动模型重新生成河道，在分叉位置之后的原河道则废弃。

⑤ 判断砂地比是否达到指定阈值，达到则模拟结束，否则转到步骤②。

⑥ 对产生的模型进行条件化处理，得到最终的随机模拟结果。

Alluvsim算法适用于河流沉积环境，可真实地再现河流相储层构型要素，如河道、点坝、天然堤、决口扇等几何形态和内在成因上的联系，进而建立真实的地质模型。针对该方法所存在的密集井数据条件化困难问题和点坝砂体内部构型刻画不足问题，国内学者对该算法做了相应改进[22-23]。Alluvsim算法也可运用在深水环境中，此时河道中线操作和构型要素需做适当调整[21]。

2 算法改进

曲流河道和深水弯曲水道在平面形态和迁移几何特征等方面具有许多相似性，如冲裂、复合水道(河道)带、侧向迁移以及截弯取直等等。然而，两者在演化方式上有显著差异。在陆上曲流河中，河道侧向迁移和向下游方向扫动是一个连续过程，垂向加积现象不明显。在深水体系中，有简单的下切和垂直堆积形成的横向不活动的复合水道，有纯向下游迁移的复合水道，有间断侧向迁移水道[26-27]。弯曲特征是深水水道最直观的几何特征。R.B.Wynn等人介绍了现代不同地区的众多深水水道，如Amazon扇、Mississippi扇和Zaire扇等，它们各自深水水道弯曲特征不同。刘新颖等人介绍了西非中部的Rio Muni盆地6条弯曲程度和规模各异的水道，不同曲率的水道表现不同的充填样式[6,28]。原Alluvsim算法中，初始河道中线根据试油资料和地震解释等能够提供的储层水平方向的趋势信息约束在河道中线库中选取，而河道中线库中每一条河道中线的位置和分布是随机的；迁移方式上，河道沿古流向整体迁移考虑不足；此外，曲流河演化程度与砂地比及产生新河道的概率有关，自身曲率难以保证。因此，为了更好地再现浊积水道分布、沿古流向整体迁移特点及其弯曲特征，笔者对Alluvsim进行改进，以分别适用于不同条件下浊积水道训练图像建立。

2.1 水道中线库生成改进

深水水道沉积早期，沉积物供应充足，侵蚀能力强，水道下切可形成大型海底峡谷底部河床。随着时间的流逝，沉积物供应相对变少，单个水道的切割、迁移和加积形成了一个明显复杂的浊积水道体系[29-30]。浊积水道体系会有一个宽度范围，而基于周期性扰动模型生成的水道中线库没有边界约束(图1a)。笔者通过对水道流线末端点做范围限制，进而约束水道中线库生成，具体实施步骤如下(图1b)：

① 确定水道流线初始点的边界范围。水道流线起始点可设置在网格某一边界上，分布服从正态分布。根据均值和标准差来确定初始点的边界范围。

② 计算水道流线末端点的边界范围。取水道流向起始点的两个端点，根据主流向分别延长两个端点，与网格边界相交的两个端点间的范围即为水道中线库末端点的边界范围。

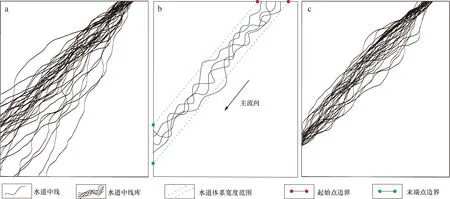
图1 水道中线库生成改进方法及改进前、后效果比较Fig.1 An improved method for channel streamline generation and results comparison of the original method and the improved onea. 水道中线库改进前；b. 水道中线库生成改进;c. 水道中线库改进后

③ 水道中线库生成。在水道流线起始点范围内根据周期性扰动模型产生水道中线，若水道流线末端点在其边界范围内，保留；否则，重新生成。

将改进前后的水道中线分布进行对比(图1)，改进前水道中线呈发散状态，位置分布差异大；而改进后水道中线在约束的河谷范围内，能够再现深水水道体系空间分布特征。

2.2 水道沿古流向整体迁移改进

在深水体系中，水道在侧向迁移过程中，水道存在向下游的分量，平面上水道向下游方向整体迁移与水道侧向迁移是一个连续或者离散的过程[5,7,30]。原Alluvsim算法中侧向迁移和向下游扫动现象是连续的(图2a)，可通过控制沉积物供给量(流量)来控制水道侧向迁移过程中向下游迁移的程度。流量小时，水道以侧向迁移为主，沿古流向整体迁移微弱；流量较大时，水道可见明显地向下游扫动的现象。为了模拟浊积水道沿古流向整体迁移的离散过程，可通过将单一水道中线上各节点沿古流向迁移来再现水道仅向下游扫动现象，节点坐标变换计算公式为：

X′i=Xi+sin(mCHazi)dist

(1)

Y′i=Yi+sin(mCHazi)dist

(2)

式中:(Xi,Yi)是各节点整体迁移前的坐标；(X′i,Y′i)是各节点整体迁移后的坐标;mCHazi是水道的主方向;dist是水道沿古流向扫动的距离，该距离根据地质人员分析获得对应统计规律并随机抽样获取。

图2b为单一水道侧向迁移和沿古流向整体迁移离散过程的模拟结果图，再现了前期侧向迁移为主后期沿古水流向扫动的浊积水道。

2.3 弯曲度指标约束水道演化改进

1) 初始水道：LI为水道流线长度，∂I可近似为水道流线长度与初始弯曲度的比值，计算两者比值求取弯曲度kI。

2) 水道截弯取直：LC根据新的水道流线长计算，∂C可近似为初始河谷长度∂I。

3) 水道侧向迁移：LL根据新的水道流线长计算，∂L可近似为初始河谷长度∂I。

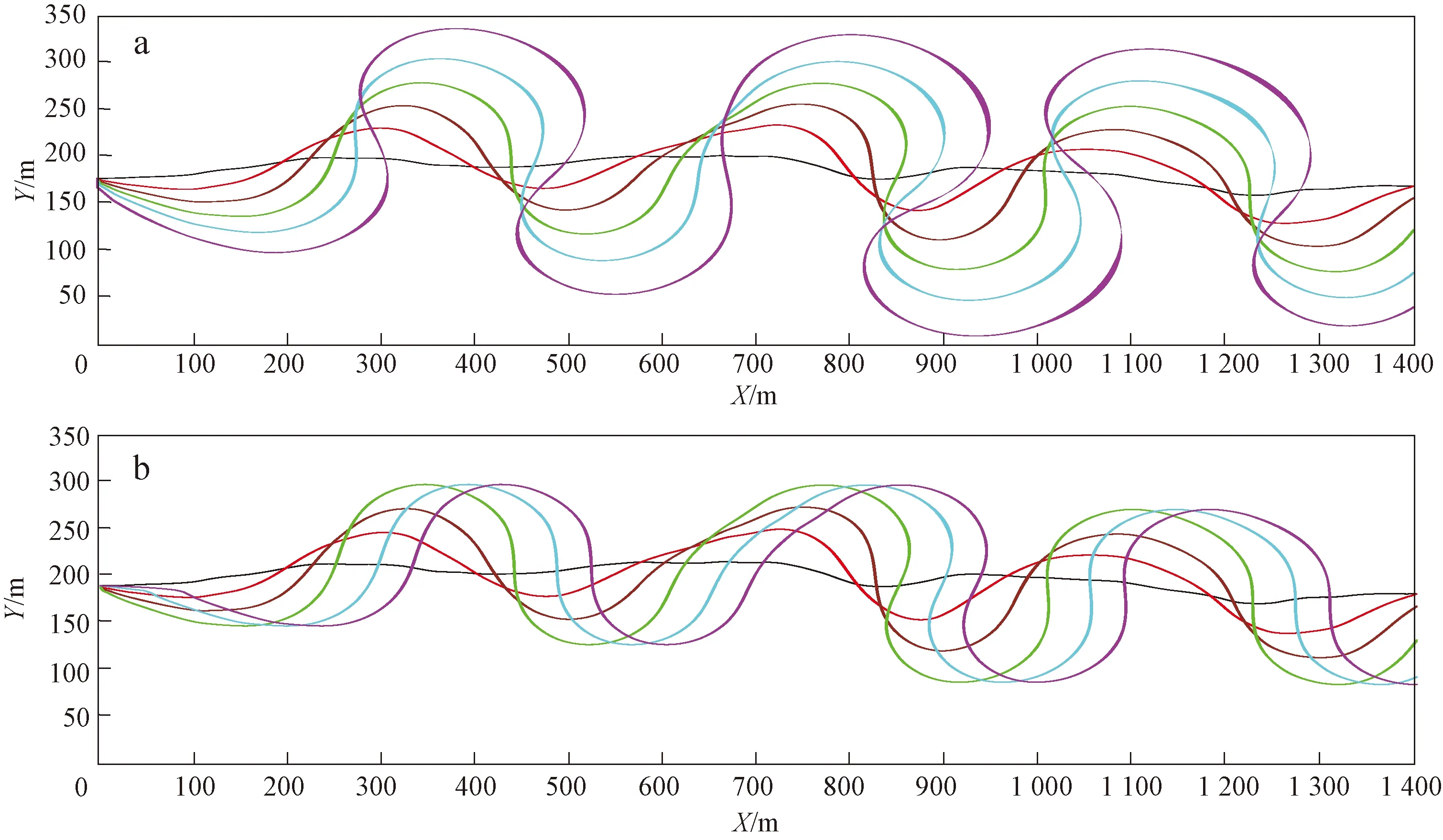
图2 单一水道平面迁移模式改进前、后效果比较Fig.2 Results comparison of the horizontal migration patterns of single channel before and after improvementa. 水道中线侧向迁移与沿古流向扫动连续(改进前)；b. 水道中线早期侧向迁移，后期沿古流向扫动(改进后)

图3 水道弯曲度计算及不同弯曲度水道生成Fig.3 Graphs showing the calculation of the channel curvature and the generation of channels with different curvaturesa. 水道弯曲度计算示意图；b. 不同弯曲度水道生成图

4) 沿古流向整体迁移：弯曲度值不变。水道沿古流向迁移伴随垂向加积时，弯曲度值不变；若无垂向加积，形成的复合水道弯曲度将变小，由于不方便计算，弯曲度近似为不变。

5) 水道改道：需分段计算，假设第m个节点前(包括第i个节点)的所有节点未移动，为一段，而第i个节点后的节点重新生成，为另一段。再根据两段各自的水道流线长除以初始河谷长度的比值之和来得到弯曲度。

每一次产生水道后计算该弯曲度，并与预期弯曲度值比较。弯曲度大于预期弯曲度时，水道演化终止。如图3b所示，生成了3期不同弯曲度的水道，水道1、水道2和水道3的弯曲度分别为1.59，1.25以及1.10。

在以上改进的基础上，形成了浊积水道训练图像生成算法(图4)，具体步骤如下：

① 统计研究区浊积水道体系形态参数。

② 水道中线库生成。根据已有地质知识库，在水道体系范围内产生一个候选水道中线库。

③ 根据几何形态参数对道中线上所有的节点赋值，建立该条水道的三维构型模型。

④ 由低到高依次选择水道加积面。根据水道垂向分布趋势计算各加积面对应的NTG(砂地比)。最大和最小加积面的高度差为浊积水道体系垂向深度。

⑤ 选择初始水道中线。以水道水平趋势分布为约束随机地从水道中线库中选择一条水道中线。

⑥ 确定水道预期弯曲度。在弯曲度变化范围内从某种分布中抽取，可以是三角分布(需知弯曲度众数)或高斯分布等，确定的该弯曲度值用来决定水道演化的最终弯曲形态。

⑦ 判断是否发生截弯取直。发生水道截弯取直后，重新计算水道弯曲度。

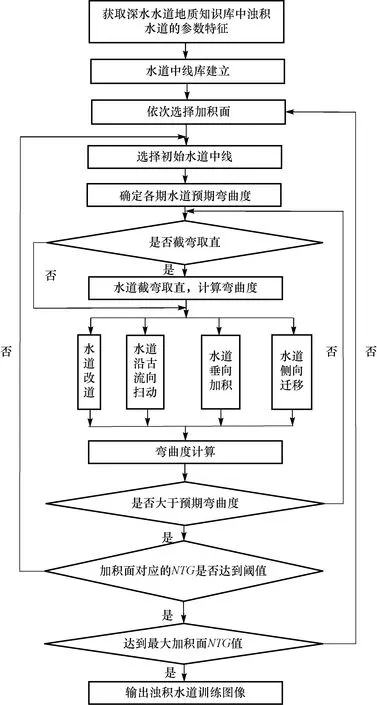
图4 浊积水道训练图像生成流程Fig.4 A flow chart showing the generation of turbidity channel training image

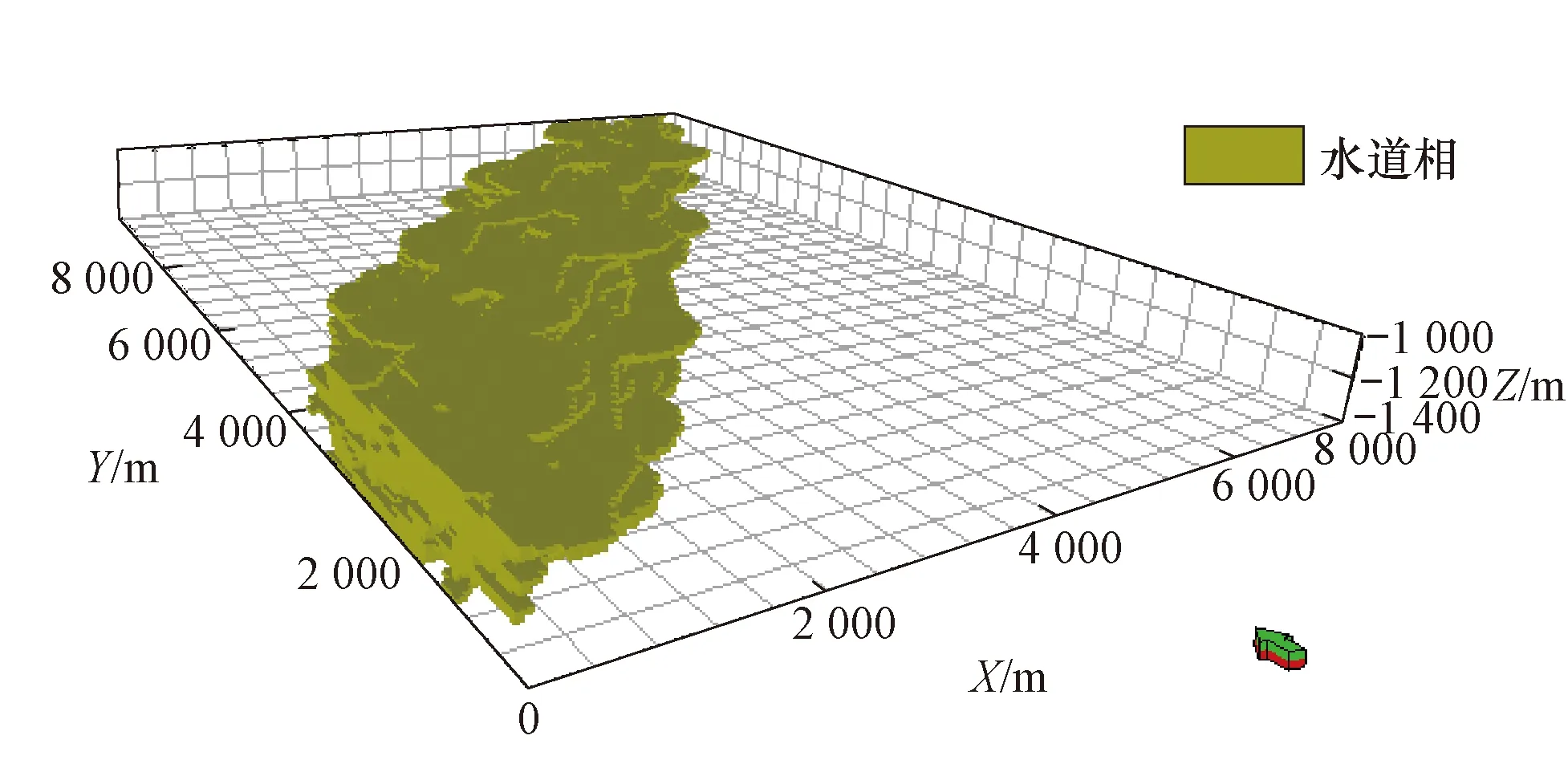
⑧ 产生下一条水道。定义了3个控制水道演化过程的概率值P1(水道发生分叉的概率)、P2(水道沿古流向迁移概率)和P3(水道垂向加积概率)，根据先验知识随机产生一个介于0～1的常数P。如果P

⑨ 判断水道NTG是否达到加积面对应的NTG。若未达到，则仍在该加积面上生成弯曲水道，转到步骤⑤；否则，转到步骤④，直到水道达到最大加积面及相应NTG值。

3 实际模型研究

以安哥拉地区某油田浊积水道为例，研究区共有25口钻井，区域大小为3.13×1010m3，地震资料显示水道主流向朝西南向(图5)，钻井资料统计得工区砂地比为0.264。前人对该区开展了精细地质研究[11,31]，获得了研究区深水水道地质知识库见表1。

在获得上述参数后，基于对研究区浊积水道地质特征的认识，采用改进的Alluvsim算法在无条件点的情况下生成了研究区的训练图像(图6)。从所建训练图像看，发育1个浊积水道体系，砂体规模为80.7×108m3，平面上水道体系宽度为1 500～2 000 m，复合水道弯曲度介于1.2～1.7。其次，剖面上水道体系下部以侧向迁移为主；水道体系中部以垂向加积为主，可见斜列式垂向迁移和摆动式垂向迁移等各种叠置样式的复合水道；水道体系上部砂体分布范围广，侧向迁移能力较强，与地质分析对比合适[12]。由此说明训练图像反映了工区地下储层结构特征，能够应用于多点建模。

图5 安哥拉地区某油田地震属性Fig.5 Seismic attributes of an oilfield in Angola

x方向网格数119x方向网格大小/m64y方向网格数179y方向网格大小/m56z方向网格数20z方向网格大小/m20砂地比0.22单一浊积水道深度/m(14,8)单一浊积水道宽深比(13,3)主方向/(°)(213,1)随机种子69 569初始弯曲度1.05时期时期1时期2时期3预期弯曲度(1.6,0.1)(1.3,0.1)(1.4,0.1)水道改道概率0.100水道加积概率00.20水道沿古流向整体迁移概率000.2垂向加积距离(水道深倍数)0(0.5,0.25)0沿古流向整体迁移距离(水道宽倍数)(0.5,0.25)0(0.5,0.25)水道加积面高度(网格楼)2,46,8,10,1214,16,18,20…

注：(a，b)表示均值为a，标准差为b。

随后将该训练图像作为参数输入，提取相应的储层模式。在此基础上，以井资料为硬条件输入，以地震属性作为辅助约束，采用Snesim方法建立了研究区三维地质模型。平面上，从三维模型(图7e，f)中抽取的3个地层切片，可见复合水道的方向大体一致，近北东向，这与地震属性对应地层切片(图7a—c)的复合水道形态较为相似。剖面上(图7h)，限制性水道体系的形态和位置与地震资料(图7g)相比也较符合。可见，多点地质统计模拟结果可较好地反映了实际储层分布。然而，模拟结果的水道构型要素难以识别，单一水道和复合水道难以划分。分析原因可能有两点：一是网格大小相对较大，有时单一水道深度小于一个纵向网格；二是本文训练图像仅划分有水道相和非水道相，其中可适当加入天然堤微相，使得相模拟过程中能更好再现水道以及水道与天然堤间的空间结构与几何特征。

图6 浊积水道训练图像Fig.6 The training image of turbidity channels

图7 安哥拉地区地震属性和多点地质统计模拟结果对比Fig.7 A comparison of seismic attributes and multi-point geostatistical simulation results in Angolaa. 地震属性地层切片2;b. 地震属性地层切片12;c. 地震属性地层切片17;d. 多点地质统计模拟结果地层切片2;e. 多点地质统计模拟结果地层切片12;f. 多点地质统计模拟结果地层切片17;g. 地震属性剖面;h. 多点地质统计模拟结果剖面

图8 安哥拉工区地震属性转换的相图和地质统计模拟结果计算的不同方向变差函数图比较Fig.8 A comparison of the phase map of seismic attribute transformation and the variogram map of diverse directions obtained by geostatistical simulation in the Angola study area a. 工区长边方向变差函数;b. 工区短边方向变差函数

最后，采用定量方法进行检验。由于该区地震分辨率较高，其整体特征能够反映地质储层实际。因此将实际地震资料计算的变差函数与模型计算的变差函数进行了比较(图8)。图8a是短轴方向比较，其中两者基台值均为0.2，块金常数分别为0.030和0.035，变程分别为2 688 m和1 920 m；图8b中基台值均为0.2，块金常数分别为0.025和0.030，变程分别为3 472 m和2 520 m。从中可以看出，两者基台值、拱高以及变程相近，形态相似，具有较高的匹配性，相关系数达到0.93，说明建立的模型能够反映地下实际，具有较高的精度。模型可以服务于后期地质以及油藏工程方面研究。