浅水低频长波对海洋核动力平台动力响应的影响分析

梁双令，程 堃

(武汉第二船舶设计研究所， 武汉 430064)

在工程设计中，波浪谱一般通过理论公式得到，这些理论波浪谱的能量主要集中在0.2～2.0 rad/s频率范围内，在0～0.2 rad/s的低频范围内，一般没有波浪能量成分。但是在实际浅水海域，伴随着大幅度振荡的波浪时历，总会出现较明显的低频波浪成分，这即是在浅水中存在的低频长波现象[1]。浅水低频长波及其诱导的一阶波浪力会导致总的波浪力大幅度增加，从而导致单点系泊船体的运动响应以及由此产生的系泊力相比于数值计算有一定幅度的增大。因此，为保证船体运动响应和系泊力预报的准确性，在总体设计流程中必须要考虑浅水低频长波的影响。

关于浅水低频长波的存在及其形成机理，已被许多理论研究和实际观测所证实[2]。为分析浅水低频长波对船体纵荡、垂荡和纵摇动力响应的影响，主要包括波浪力和运动响应，许多学者都采用数值计算与水池试验相结合的方法。肖龙飞等[3]通过频域数值计算和模型试验研究，分析了浅水不规则波浪谱中低频成分对低频纵荡运动的影响，结果表明浅水低频纵荡运动响应主要是一阶的，二阶成分几乎可以忽略。李欣等[4]在线性三维势流理论的基础上，采用时域计算方法分析了浅水软刚臂系泊FPSO的触底情况，并与模型试验进行了对比。郭彬[5]通过时域数值计算和模型试验分析了船体在浅水非共线风浪流海况作用下的运动性能与舷侧甲板上浪情况。

本研究针对作业于渤海浅水海域的海洋核动力平台示范工程，通过数值计算和水池试验两种方法得到浅水波浪谱密度，通过结果对比，分析浅水低频长波对平台纵荡、垂荡和纵摇三个自由度上的波浪力和运动响应的影响。

1 理论基础

1.1 纵荡运动方程

单点系泊平台在迎浪不规则波作用下的纵荡运动方程可表示为[6]：

(1)

式中：x1为纵荡运动；a11(μ1)和B11(μ1)分别为固有频率μ1对应的附加质量和静水阻尼系数；C11为单点系泊系统提供的等效线性纵荡水平回复力系数；F1为纵荡波浪力，包括一阶成分和二阶成分。

对于一阶波浪力，其谱密度函数可直接根据波浪谱密度函数S(ω)和波浪力幅值响应函数HF1(ω)计算，如式(2)所示，其标准差可由式(3)计算得到。

(2)

(3)

二阶平均波浪力决定了平台的平均位移，可以表示为：

(4)

式中，T(ω,ω)为平均波浪力二次传递函数。

二阶波浪慢漂力谱密度函数如式(5)所示，而其标准差可由式(6)计算得到。

(5)

(6)

式中，T(ω+μ,ω)为波浪慢漂力二次传递函数。一阶波浪力和二阶波浪慢漂力决定了平台在平均位移附近的运动幅度。

对于一阶纵荡运动，其谱密度函数也可由波浪谱密度函数S(ω)和运动幅值响应函数Hx1(ω)计算，如式(7)所示，其标准差可由式(8)计算得到。

(7)

(8)

以二阶低频纵荡波浪力作为输入，以二阶低频纵荡运动作为输出，二者的能量谱密度函数关系可以通过线性幅值传递函数进行表示，如式(9)所示。

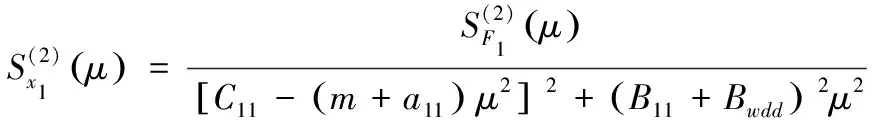
(9)

(10)

由式(10)可知，二阶低频纵荡运动不仅受二阶纵荡波浪力影响，也与运动阻尼、回复力系数有关。其中回复力系数与单点系泊系统的设计有直接关系，在本文讨论平台动力响应时，假设其为常量。因此影响纵荡运动响应大小的因素主要有纵荡波浪力和运动阻尼，而后者又包含静水阻尼和波浪慢漂阻尼两部分。

静水阻尼系数与黏性有关，一般根据静水衰减试验结果计算得到，如式(11)所示[8]。

(11)

(12)

式中：n为纵荡衰减次数；xn为第i次纵荡运动幅值。

纵荡波浪慢漂阻尼是由波浪引起的，可以通过平均波浪力的二次传递函数计算得到，如式(13)和(14)所示[9]。

(13)

(14)

1.2 垂荡和纵摇运动方程

对于垂荡和纵摇运动，由于其固有频率处在波频范围内，所以主要表现为一阶运动，而且其自身静水回复力远大于系泊系统提供的回复力，因此一般在频域计算中不考虑系泊系统的影响。基于线性势流理论，自由漂浮的平台在频率ω的规则波作用下的一阶运动方程如式(15)所示。

(15)

与纵荡一阶波浪力和运动响应相同，垂荡和纵摇一阶波浪力的谱密度函数和标准差可通过式(2)和式(3)计算得到，垂荡和纵摇运动响应的谱密度函数和标准差可通过式(7)和式(8)计算得到。

2 海洋核动力平台简介

海洋核动力平台是我国核动力水面舰船示范工程，属浮动式核动力能源保障船式平台，由软刚臂单点系泊装置长期定位于渤海海域，主要解决渤海油气开采中的电力、淡水等能源需求。

平台有两部分组成：船体和软刚臂单点系泊系统，分别如图1和图2所示。平台作业场址平均海平面30.6 m，设计重现期为500年。基于国家海洋环境预报中心监测数据，推算得到重现期500年最低水位相对于平均海平面为-5.1 m，因此平台的最小作业水深为25.5 m，属于浅水海域。

图1 船体网格划分示意图

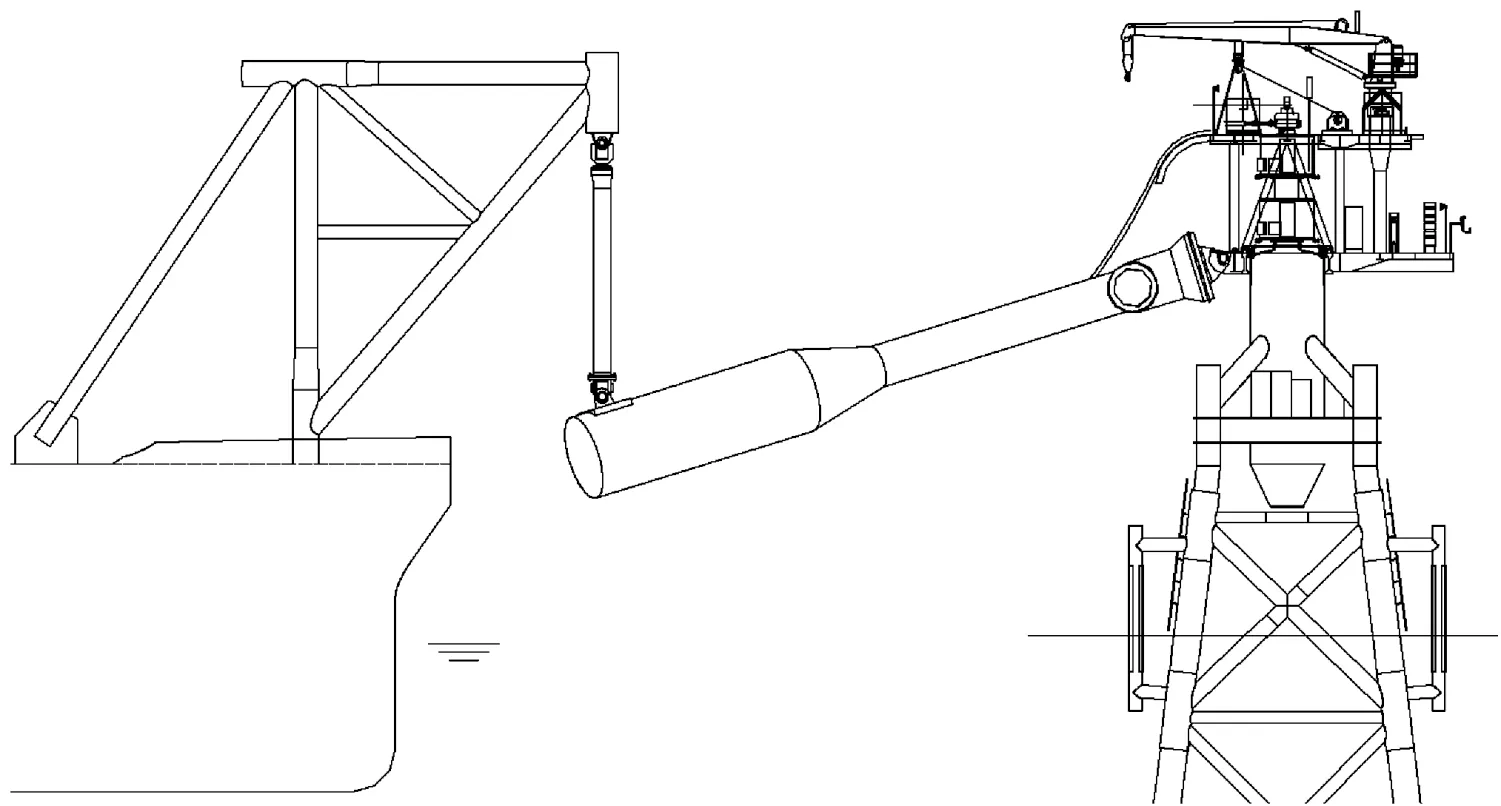
图2 软刚臂系泊系统总体布置

单点系泊系统的纵荡水平回复力曲线如图3所示，图3中x为纵荡位移，Fx为纵荡水平回复力，二者成非线性关系，尤其是当位移比较大时更为明显。

基层思想政治工作是促和谐、保稳定的生命线，是企业生产经营管理实现良性发展的有力思想保证。基层思想政治工作发挥着统一思想、提高认识，化解矛盾、理顺情绪，凝聚力量、振奋精神的重要作用，是协调关系、理顺情绪的润滑油，是宣传政策、解惑释疑的稳压器，是统一思想、鼓舞士气的凝固剂。它虽然不直接产生经济效益，但它犹如水、空气对于人一样，是确保基层和谐、稳定发展的生命线。

图3 单点系泊系统纵荡水平回复力曲线

3 数值计算结果与比较分析

3.1 不规则波校验

本研究选取在上海交通大学海洋工程水池中模拟的一组不规则波，Hs=5.0 m，Tp=10.3 s，γ=3，JONSWAP谱。波浪谱密度的计算值与试验值如图4所示。

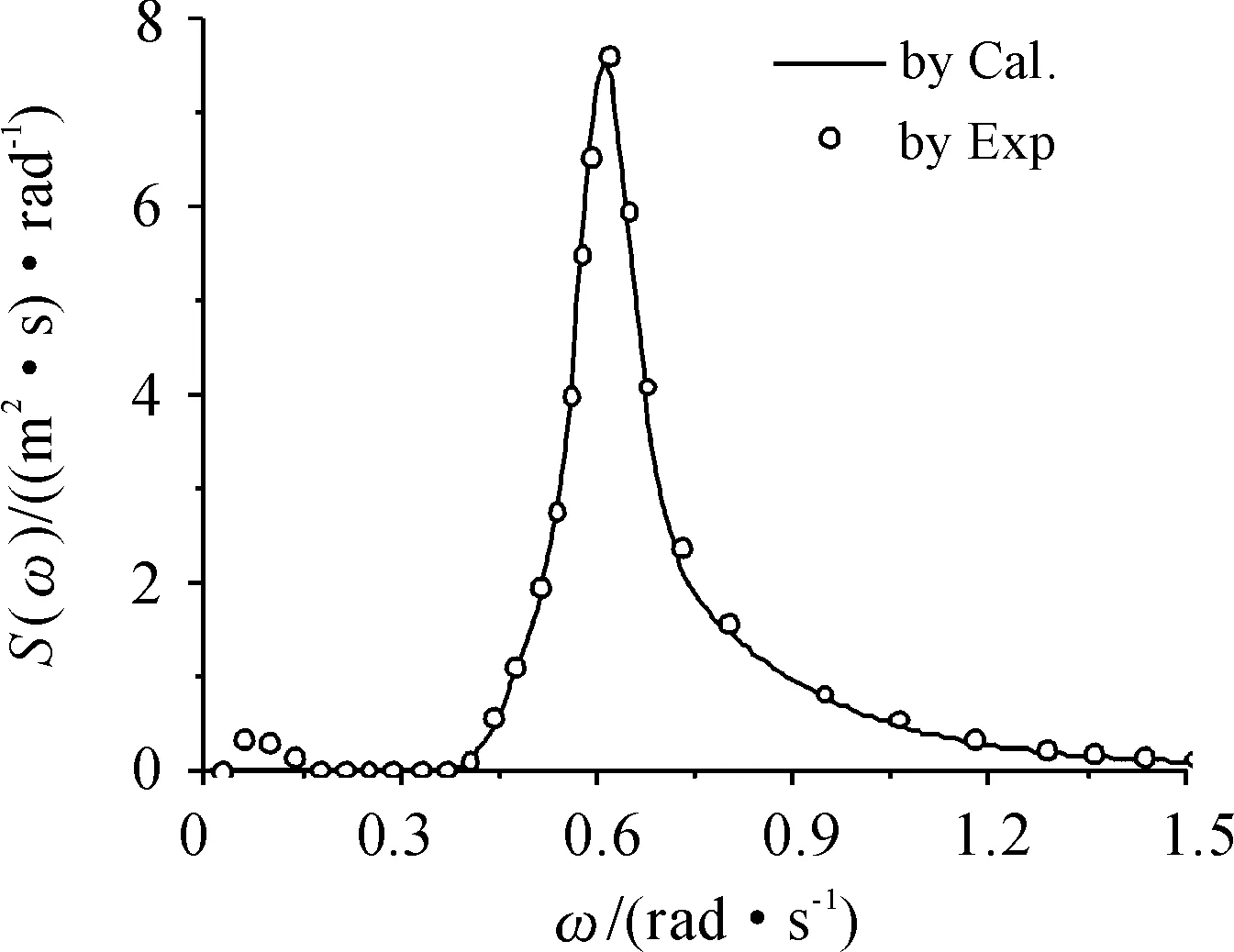
图4 波浪谱密度计算值与试验值对比结果

由图4可知，波浪谱密度计算值与试验值吻合良好，但试验值在0～0.2 rad/s的低频范围内出现了计算值所没有的能量成分，这即是在浅水中出现的低频长波现象。该浅水低频长波的存在，将对平台的运动响应和单点系泊系统的设计产生重要的影响，在实际工程设计中需要给予考虑。

3.2 纵荡动力响应

根据式(2)、式(4)、式(5)可分别计算得到纵荡一阶波浪力谱、二阶平均波浪力和二阶波浪慢漂力谱，分别如图5～图7所示。为分析浅水低频长波对纵荡波浪力的影响，以标准差为判断标准，在波浪谱计算值和试验值两种情况下的纵荡一阶波浪力和波浪漂力标准差无因次比值以及平均波浪力大小的无因次比值如图8所示。

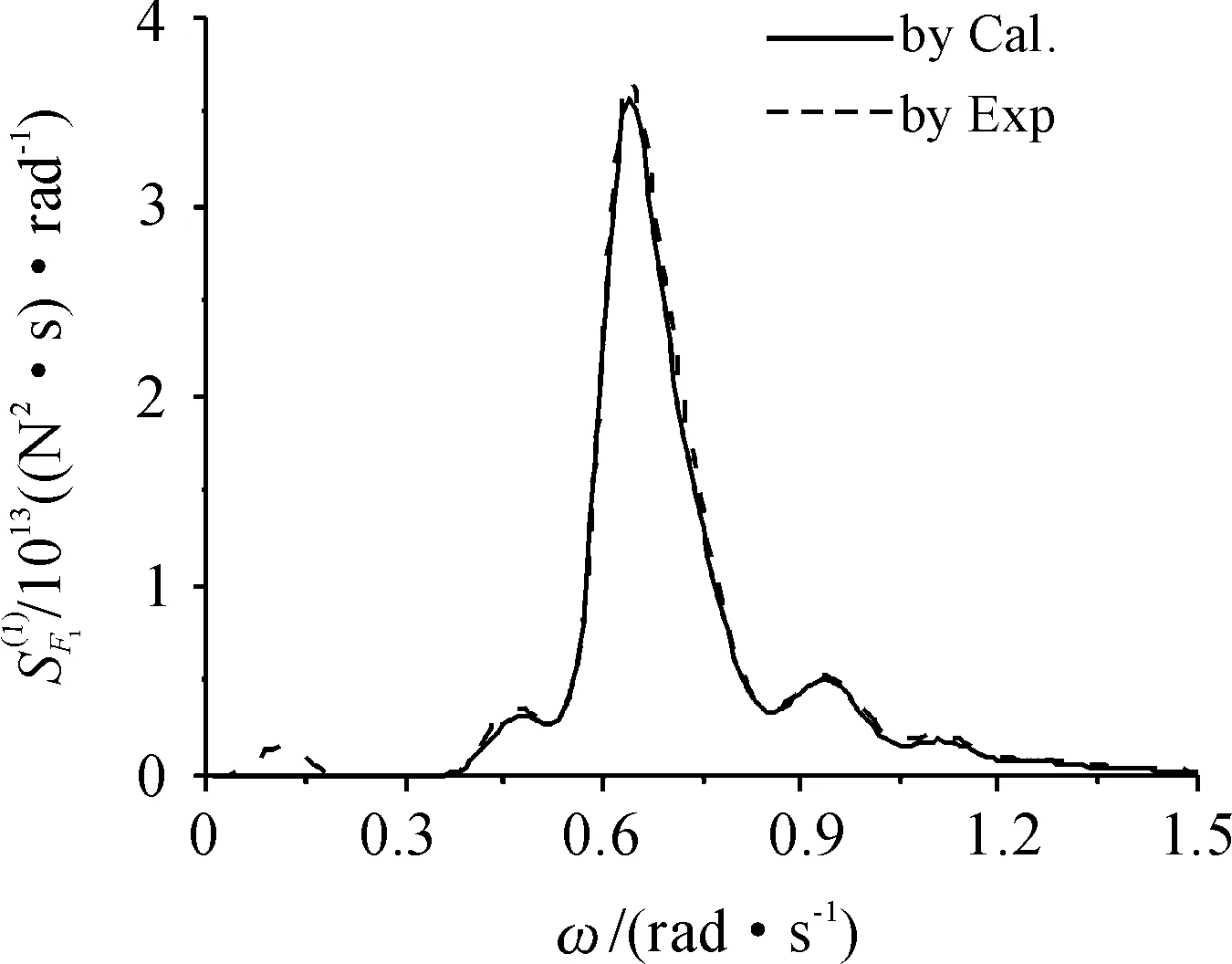
图5 纵荡一阶波浪力谱

图6 纵荡二阶平均波浪力

图7 纵荡二阶波浪慢漂力

图8 纵荡波浪力标准差对比

对比波浪谱计算值和测量值两种计算结果：

1) 对比图5和图7可知，在0～0.2 rad/s的低频范围内，一阶波浪力为1012量级，二阶波浪慢漂力为1011量级，两者相差十倍至几十倍。这说明，在浅水海域，由于低频长波的存在，低频波浪力的主要贡献为一阶低频波浪力，这一点与深水海域截然不同。

2) 由图8可知，浅水低频长波对纵荡一阶波浪力、二阶平均波浪力影响较小，而对二阶波浪慢漂力影响较大，考虑浅水低频长波相比于不考虑浅水低频长波时二阶波浪慢漂力增大一倍左右。

由式(4)计算得到平均波浪力大小为186.8 kN，重现期500年对应迎风迎流条件下的风载荷和流载荷分别为340.4 kN和33.8 kN，因此对应平均系泊力为561.0 kN。由图3可知，在该平均系泊力下，平台的平均位移为-1.70 m，此时系泊系统的纵荡水平回复力系数C11(位移处取斜率)为3.48×105N/m，则纵荡固有频率μ1可由式(16)计算得到。

(16)

式中，a11(∞)为频率为∞时的纵荡附加质量，此时μ1为0.104 rad/s。

根据式(11)和式(13)分别计算得到B11和Bwdd为1 001.1 kN·s/m和39.8 kN·s/m。因此可由式(8)和式(10)计算得到平台的一阶纵荡运动、二阶低频纵荡运动和总的纵荡运动的标准差，如图9所示。

图9 纵荡运动标准差对比

3.3 垂荡和纵摇动力响应

垂荡和纵摇一阶波浪力谱如图10和图11所示，一阶运动响应如图12和图13所示，同样以各自的标准差无因次比值分析浅水低频长波对垂荡和纵摇波浪力与运动响应的影响，如图14所示。

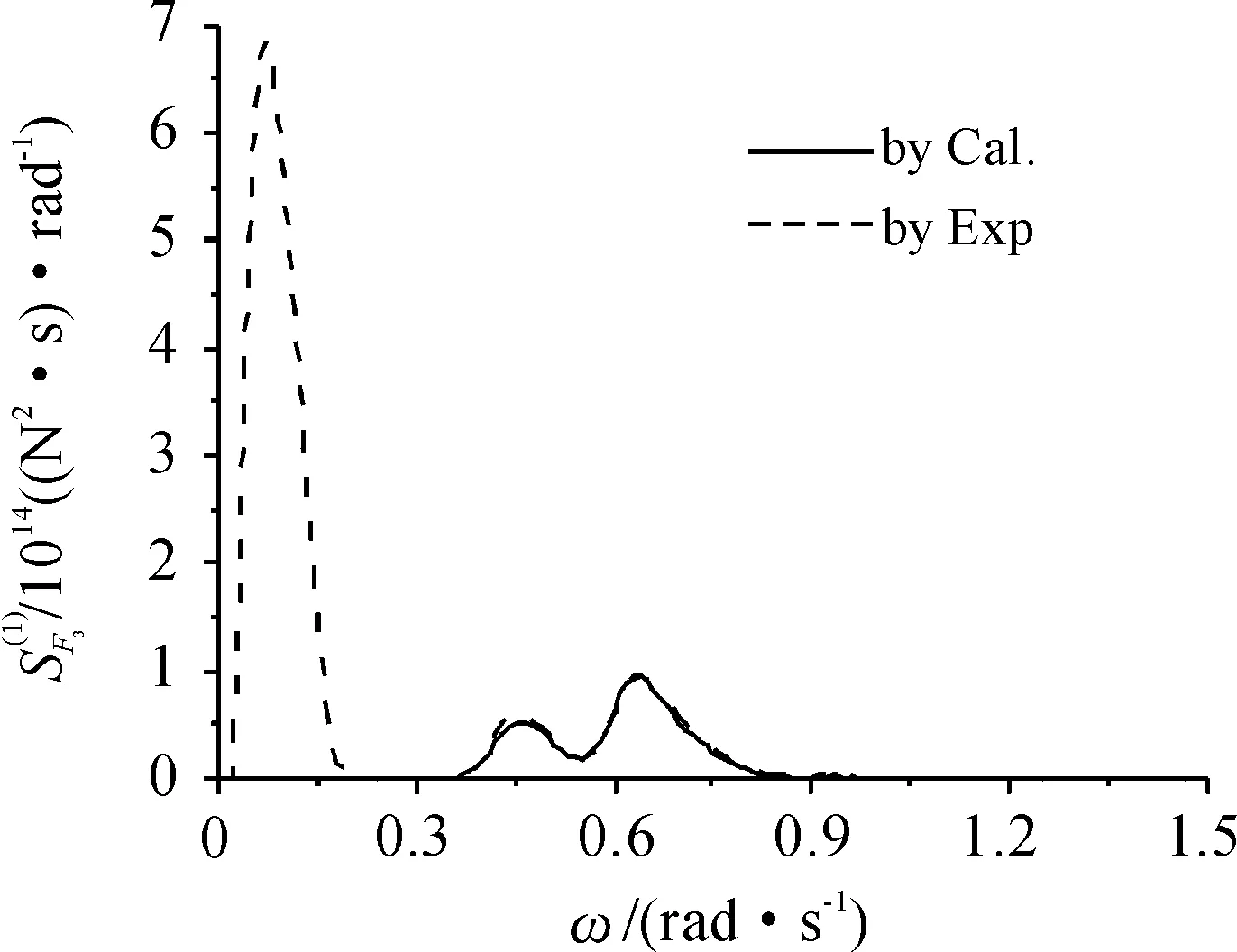
图10 垂荡一阶波浪力谱

图11 纵摇一阶波浪力谱

图12 垂荡一阶运动响应谱

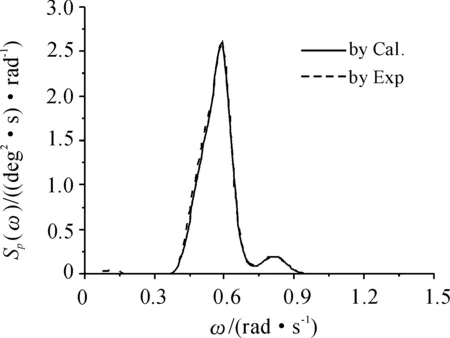
图13 纵摇一阶运动响应谱

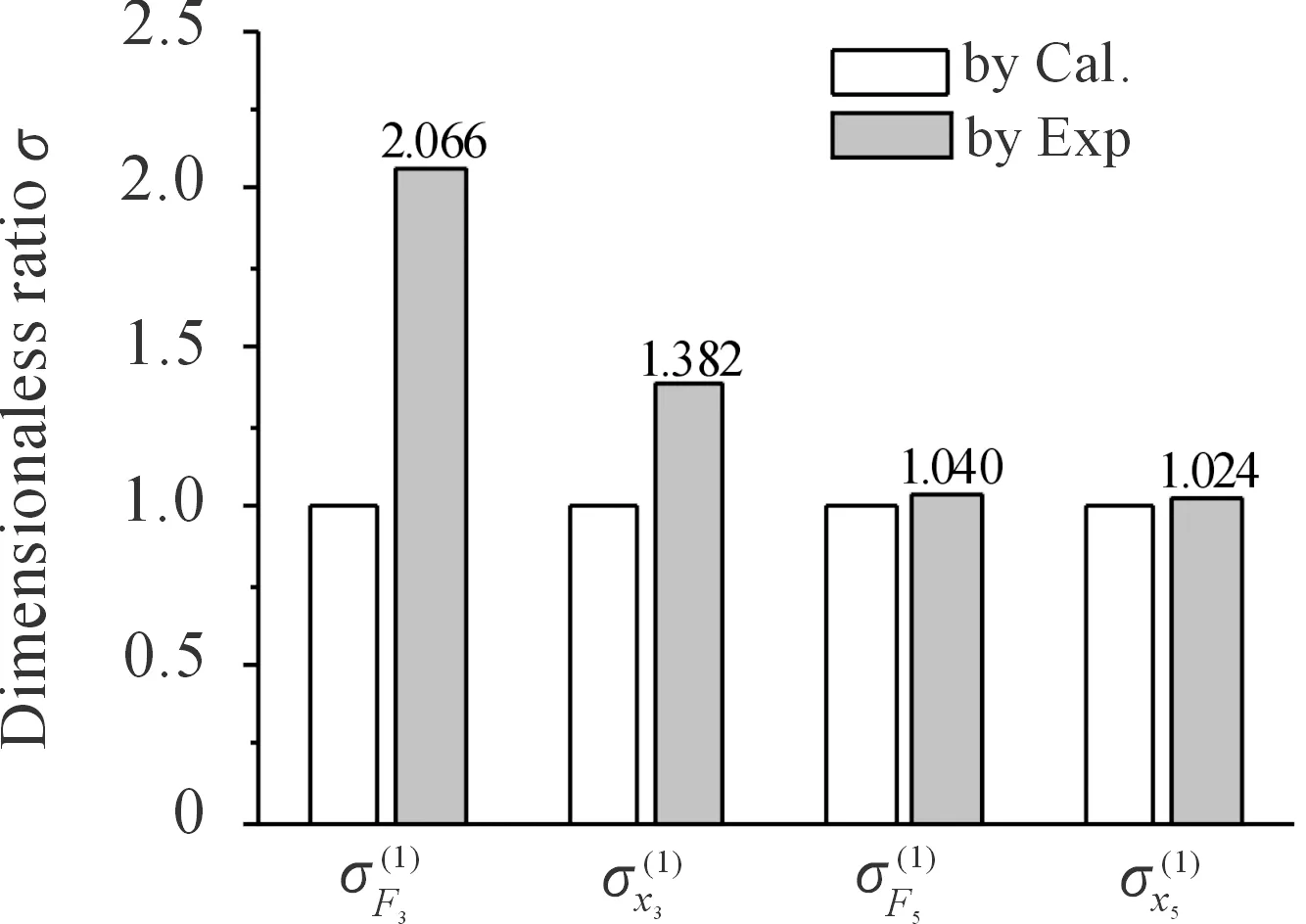
图14 垂荡和纵摇一阶响应标准差对比

对比波浪谱计算值和测量值两种计算结果：

1) 由图10和图12可知，浅水低频长波对垂荡波浪力和运动响应的影响较大，而且主要集中0～0.2 rad/s的低频范围内。

2) 由图14可知，浅水低频长波使得垂荡波浪力增大一倍左右，相应的使得垂荡运动响应增大38.2%，而对纵摇波浪力和运动响应影响较小。

4 结论

1) 浅水低频长波在一般数值计算所应用的不规则波理论中是不存在的，由于其对平台的波浪力和运动响应十分重要，在理论预报时必须予以特别重视。

2) 浅水低频长波的存在对平台二阶纵荡波浪慢漂力和一阶纵荡运动响应影响很大。

3) 浅水低频长波使得一阶垂荡波浪力和运动响应在低频范围内出现了较大的能量成分，说明其对垂荡低频响应影响很大。