基于NSGA-Ⅱ的通信星座重构方法研究

汉京滨,张雅声,汤亚锋,周 童

(1.航天工程大学 研究生院， 北京 101416； 2.航天工程大学，北京 101416)

2018年4月10日，美国参联会发布最新版《太空作战》联合条令(JP3-14)[1]，取代2013年版的旧版条令，其中提出了一个全新的作战领域——太空联合作战领域。将太空划入作战领域，一方面展示了美国对航天资产的强烈依赖性，另一方面也体现其在太空领域强烈的冲突意识。我国向来提倡和平利用太空，但面对太空中可能遇到的有意或无意的威胁，开展太空体系弹性研究，建设具有优良弹性的太空装备体系势在必行。通信卫星具有覆盖范围广、超视距连通等能力，不需要地面的通信链路就能够快速为覆盖区域的用户提供通信能力，为作战指挥、战场环境保障提供重要支撑，具有极强的战略和战术意义。保证通信星座在应对各类不利事件时的可用性与可靠性是十分有必要的。

近些年来，空间重要性日益显著，太空竞争日趋激烈，国内外学者对星座重构展开相关研究，并取得一定的研究成果。张雅声[2]针对不同星座构型，在有卫星失效情况下，提出调整相邻卫星、均匀相位和均匀星座等不同重构策略，保证在最短时间内以尽量小的能量消耗代价修复受损星座。胡伟[3]以混合星座全球导航星座中三颗MEO卫星失效情况为研究对象，以全球可用导航时间为优化目标，采用遗传算法求解重构构型。由于仅针对全球可用导航时间指标进行优化，重构时间和所需燃料消耗方面难以保证是最优方案。李晶[4]以COMPASS导航星座为研究对象，分析部分卫星失效后的星座性能，并提出利用星座外飞行器进行任务重构。该重构由于设备兼容性与连通性等技术问题，实际实施具有一定难度。赵双[5]提出基于遗传算法的导航星座重构设计，针对不同轨道面卫星失效情况提出了有针对性的重构方案，并设计了基于快速发射的导航星座重构方案，为导航星座应急重构提供参考。此外，于小红[6]、杨洋[7]等学者也进行了相关研究，取得了一定的研究成果。

由相关文献研究进展可知，当前星座重构主要研究对象为导航星座，优化指标也是针对导航星座性能制定的，并不适用于通信星座重构分析。针对这一问题，开展中高轨通信星座重构方法研究，为受损的中高轨通信星座提供合理、高效的星座重构方案。

1 星座重构优化问题分析

1.1 重构指标

1.1.1基于区域重要度的全球覆盖率

基于区域重要度的全球覆盖率，是指基于不同区域的重要程度和覆盖率所确定的全球覆盖率，是体现通信星座覆盖能力的重要指标。此前研究的覆盖区域或是针对全球覆盖，或是针对某一区域，覆盖区域内部重要程度均相同。然而，在实际应用中，由于任务需要、国家利益等原因，对于全球不同区域必然存在不同的通信需求程度。

基于以上考虑，提出基于区域重要度的全球覆盖率指标。根据经纬度，将全球划分为18×36的网格区域，每个网格大小为10°×10°。根据所在区域的通信需求程度，将重要度等级分为必需、急需和一般需求三个等级。以美国为例，假定区域重要度分布如图1所示，必需为红色，急需为黄色，一般需求为无色。

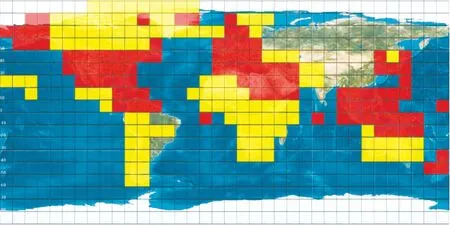
图1 区域重要度分布

此时，基于区域重要度的全球覆盖率C为：

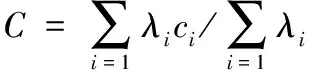
(1)

式(1)中，ci为通信星座在一个回归周期内对i区域的平均覆盖率；λi表示为i区域重要度。

1.1.2重构时间

重构时间，是指通信星座受损后进行星座重构所需的时间，是衡量星座重构方案的重要依据。由于卫星在进行轨道机动时无法提供通信功能，参与重构的卫星越多，重构花费时间越长，通信星座在此期间的能力损失越严重。因此，在设计星座重构方案时，应尽量减少需要进行轨道机动的卫星，并尽可能缩短重构卫星进行轨道机动的时间，尽量使更多的卫星能够在星座重构时仍为地面单位提供通信功能。此时，将所有需要进行轨道机动的卫星重构时所消耗的时间之和定义为重构时间Trec，其表达式为：

(2)

式(2)中，ti为第i颗卫星重构时所需消耗的时间；n为所需重构的卫星数。

1.1.3重构能量

重构能量，是衡量星座重构方案所需消耗能量的指标。由于卫星位于GEO轨道，发射难度大、成本高，在不考虑在轨能量加注的前提下，每一份能量都十分宝贵。同时，由于卫星剩余能量在一定程度上决定了卫星的剩余寿命，在进行重构优化时，应尽量减少能量消耗。此外，星座的性能取决于每一颗卫星的工作能力，当有卫星失效时，必然会造成星座通信性能的下降。在进行重构时，应尽量保证星座内各卫星的剩余能量不会有太大差异，避免某颗卫星由于能量耗尽而失效，致使星座能力下降，影响星座整体服役时间。因此，在评价重构能量时，考虑从重构所需消耗总能量和消耗能量均衡度两个角度进行优化。

重构所需消耗总能量，是指所有参与重构卫星在进行轨道机动时所需消耗的能量之和，这里用总速度增量ΔVall进行表示，即：

(3)

式(3)中，n为星座所需重构的卫星数量；ΔVi为第i颗卫星重构时所需的总速度增量；αi为根据第i颗卫星剩余能量确定的能量权重因子。卫星剩余能量越多，能量权重因子越小，剩余可用能量越少，能量权重因子越大，以此降低剩余能量相对较少的卫星进行轨道机动的可能，尽可能保证每颗卫星剩余能量相差不大。

消耗能量均衡度，是衡量星座内各卫星在星座重构时所需消耗能量差异性的度量，用Prec表示。并将各卫星在此次重构中所需的速度增量的方差作为衡量这一指标的标准。该值越小，则说明各卫星在星座重构中消耗的能量越相似，对各卫星寿命的影响越接近，不会对星座整体服役计划产生太大影响。其表达式为：

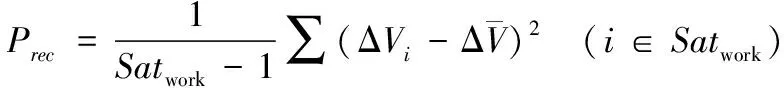
(4)

(5)

1.2 轨道机动模型

进行星座重构，即星座内正常工作的卫星通过轨道调整，改变卫星站位，优化星座结构及性能。在进行星座重构时，要充分考虑卫星当前状态，权衡重构代价与收益，通过尽可能少的轨道机动实现较高的性能提升。

在进行星座重构优化计算前，要对轨道机动进行约束，明确约束条件，节省时间的同时也可以使优化结果更加合理可信。由于重构所需能量为卫星提供，十分有限，因此一般不对卫星轨道进行太大的改变。重构所需涉及的轨道调整主要分为两种：轨道面调整和同轨道内调整。

轨道面调整时，速度增量是与卫星在轨运行速度直接相关的函数，即使是很小角度的轨道机动，也需要很大的速度增量，而进行星座重构时需要调整的轨道面夹角普遍较大，一旦进行轨道机动，将严重影响卫星寿命。因此采用轨道面调整进行轨道重构性价比不高。

同轨道内调整时，初始轨道与目标轨道处于同一轨道，只是存在一定的相位差，此时必然存在如下关系：

(6)

式(6)中，a为轨道半长轴；e为轨道偏心率；i为偏心率；Ω为升交点赤经；ω为近心点辅角；1为初始轨道，2为目的轨道。

根据初始位置与目标位置的关系，又可以分为目标超前同轨机动和目标滞后同轨机动。如图2所示，通过施加至少一对大小相等、方向相反的速度增量，可以实现轨道调整。

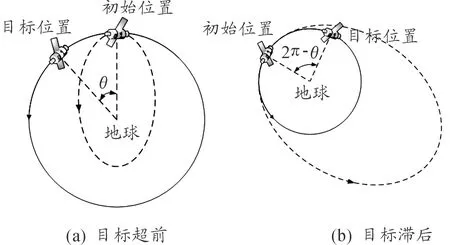
图2 目标超前与目标滞后同轨机动

目标超前时，目标位置与初始位置间的地心角为θ，则航天器需要进入低轨过渡椭圆轨道，缩短轨道周期后，变轨回到原轨道，实现目标超前同轨机动。此时存在关系式[8-9]：

(7)

式(7)中，r为初始轨道半长轴；μ为地球引力常数；rp为椭圆轨道短半轴。

可以得出：

(8)

在实际应用中，发动机推力较小，一般不会一次性提供较大的速度增量。此时，可根据任务期望恢复时间Trec来确定卫星在转移轨道的圈数ntra有：

(9)

式(9)中，轨道机动时所需调整的轨道倾角θtra=θ/ntra。

此时的轨道机动消耗为：

(10)

目标滞后时，目标位置与初始位置间的地心角为θ，则航天器需要进入高轨过渡椭圆轨道，增大轨道周期后，变轨回到原轨道，实现目标滞后同轨机动。此时存在关系式：

(11)

式(11)中，ra为过渡椭圆轨道长半轴。

轨道机动消耗为：

(12)

以半长轴为42 166.3 km的GEO轨道和半长轴为16 732.1 km的MEO轨道为例，分别计算目标超前和目标滞后30°、60°和90°时重构时间与速度增量的关系，如图3所示。

图3 重构时间与速度增量关系曲线

可见，地心角θ相同时，目标滞后轨道机动所需的速度增量略大于目标超前轨道机动所需的速度增量，且GEO轨道所需的速度增量比MEO轨道所需的速度增量略大。当轨道高度相同时，随着地心角θ的增大，轨道机动所需的速度增量也在增加，且随着重构时间的增长，目标超前与目标滞后所需的速度增量的差距在逐渐缩小。此外，由于GEO轨道周期为1天，且目标滞后轨道机动所需最小时间大于轨道周期，因此当重构时间为1天时，在目标滞后的情况下无法完成轨道机动。

2 基于NSGA-Ⅱ算法的星座重构方法

由于中高轨通信星座的卫星数量相对较少，星座构型也比较简单，当出现卫星失效时，主要根据任务需求和专家经验进行变轨机动，重构方案能够实现任务需求，但不一定是最优的。随着近些年多目标优化算法的兴起，通过仿真软件进行建模分析的方法逐渐成为解决多目标优化问题的主要途径。

2.1 星座重构的变量编码方式

进行星座重构时，不仅要确定哪几颗卫星参与重构，还要确定参与重构卫星的真近点角变化度数。然而，重构卫星数量的变化导致染色体长度的变化，这将不利于优化算法中杂交、变异等过程的运算。因此，拟采用双层基因编码确定变量信息。

上层基因Si决定该方案内星座中的哪些卫星参与重构，表示为：

(13)

式(13)中，i=1,2,…,n表示第i颗卫星。

将星座内所有卫星按照序号顺序排列为一串长度固定的基因，作为该方案下双层基因的上层基因，决定该方案下需要参与重构的卫星。下层基因fi决定重构卫星需要变化的真近点角度数，nmax决定重构卫星在转移轨道驻留的圈数。

如图4所示，随机为星座内每颗卫星生成0°～360°的真近点角，并根据任务期望恢复时间确定最大驻留圈数nmax，在0至nmax间随机生成卫星在转移轨道的驻留圈数ntra。当上层基因为1时，该真近点角即为卫星调整后的真近点角，当上层基因为0时，卫星的真近点角为原真近点角。

图4 染色体编码示意图

2.2 Pareto占优思想

多目标优化算法自20世纪50年代提出以来，大量学者进行了相关研究，提出先验法、渐进法、后验法等思路。经过多年的探索实践，基于Pareto优化策略的优化思想成为其中应用较为广泛的思想之一[10]。

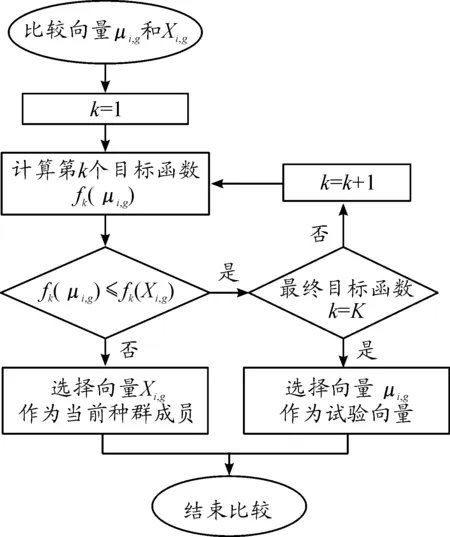
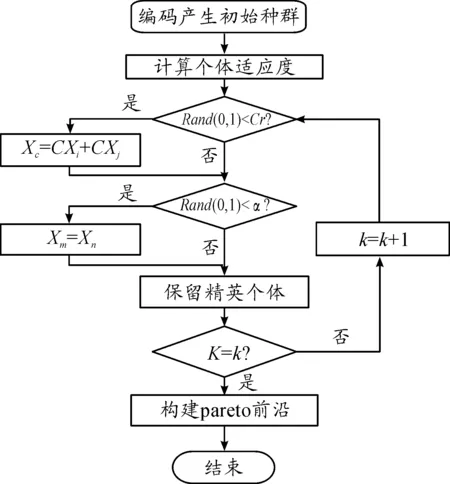
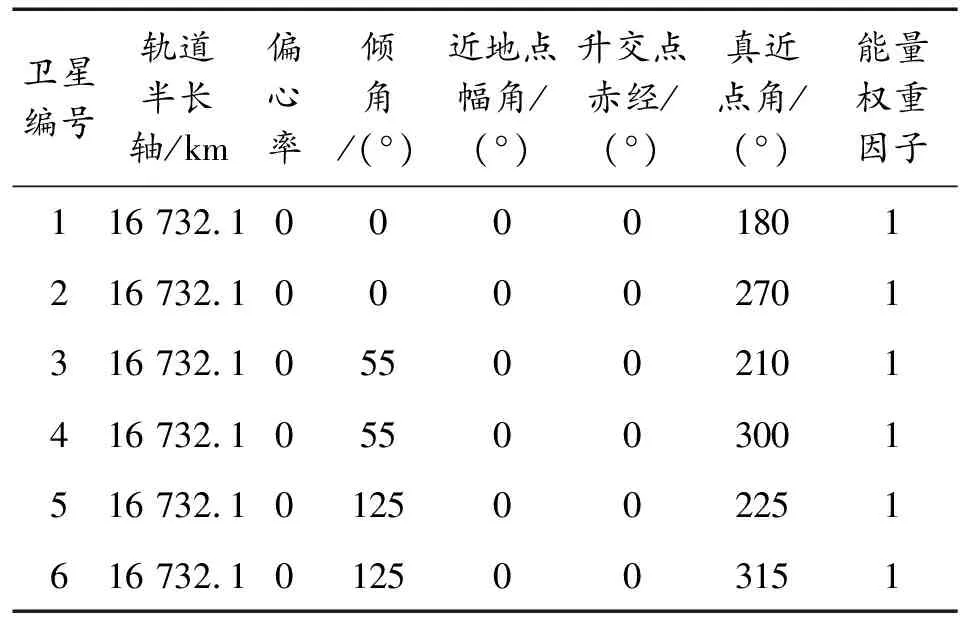
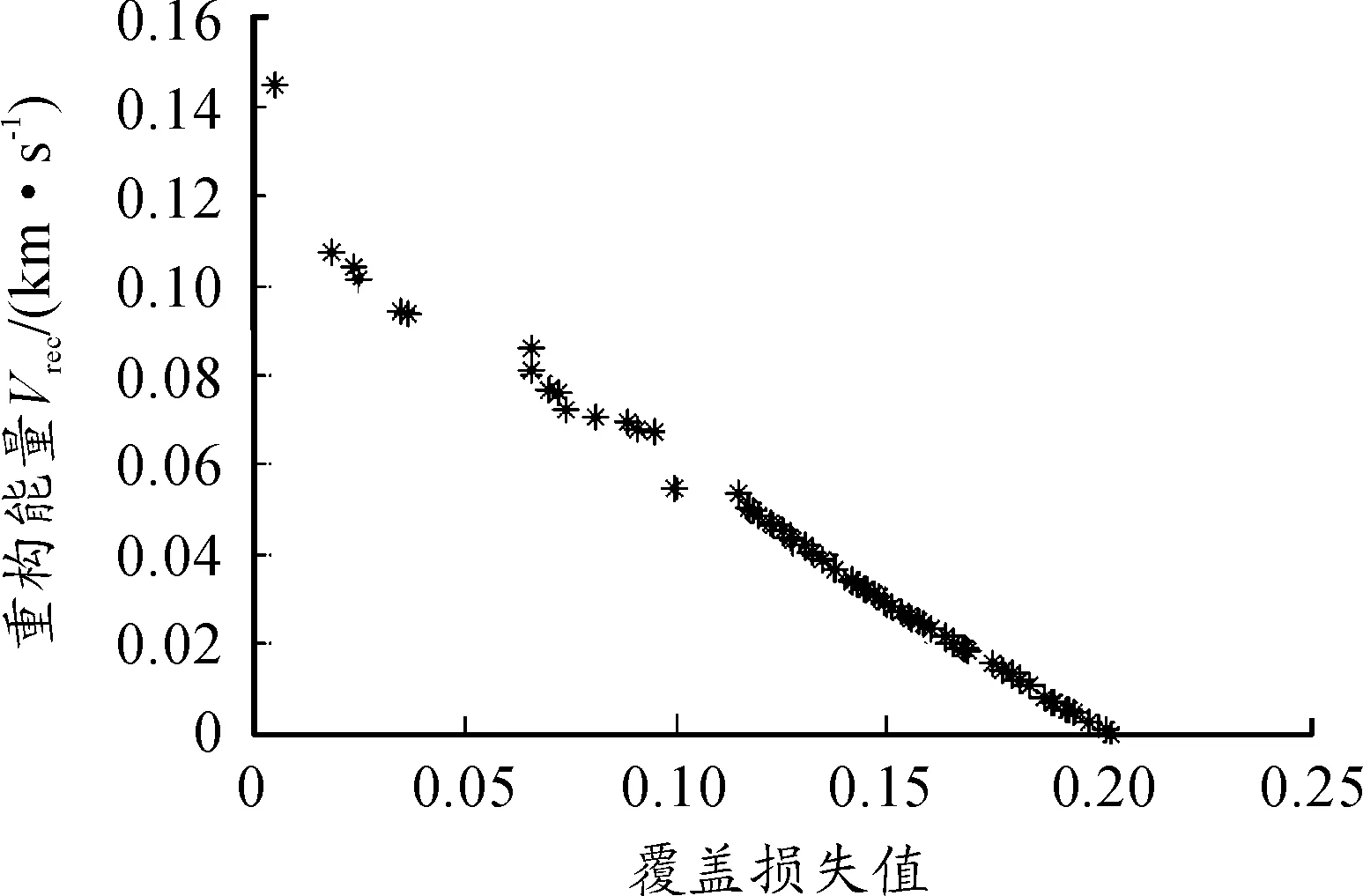
在多目标优化中，当求最小值问题minf(x)时，若可行解x1存在任一目标值fk(x1)均小于等于另一可行解x2中的对应目标值fk(x2)，且存在某个目标值fj(x1)小于另一可行解x2中的对应目标值fj(x2)，则称可行解x1相比于x2占优或x1支配x2(记x1

∀k∈{1,2,…,K}∶fk(x1)≤fk(x2)

且∃j∈{1,2,…,K}∶fj(x1)

(14)

通过优化算法的逐代寻优，将所有非支配解的集合构造为非支配解集，即Pareto前沿。这里选择评价次数最小的Pareto占优选择流程[11]，其公式为：

(15)

式(15)中，Xi,g为目标向量；μi,g为试验向量。即若Xi,g不支配μi,g，则选择μi,g。具体流程如图5所示。

2.3 NSGA-Ⅱ算法及其主要流程

NSGA(Non-dominated Sorting Genetic Algorithm)算法是Srinivas和Deb于1993年提出的优化算法[12]。在该算法的基础上，Deb等人于2000年提出NSGA-Ⅱ算法，降低了构造最优解集时的复杂度，并引入精英策略和密度函数，通过计算拥挤度和非支配层级确定非支配序列，改进了NSGA 算法的大部分缺陷，使其成为应用最广的多目标优化算法之一[13-15]。

图5 基于选择规则的Pareto占优选择流程框图

NSGA-Ⅱ算法简洁高效，主要包括初始化、杂交、突变等步骤，具体流程如图6所示。

图6 NSGA-Ⅱ算法流程框图

图6中，Cr为杂交概率，α为突变概率，Xc为杂交产生的新个体，Xi、Xj为种群中的随机个体，Xm为突变产生的新个体，Xn为新生成的个体，K为进化代数。

3 仿真实例

3.1 受损星座参数设置

仿真平台为Matlab 2010a和STK9。设定通信星座为中轨通信星座奥德赛星座所采取的轨道。星座由3个轨道面组成，轨道倾角为55°，每个轨道面均匀分布4颗卫星。由于某种不利事件，致使6颗卫星失效。此时需要通过星座在轨重构尽快恢复全球通信功能，满足各地通信需求。剩余可用卫星参数值见表1。

表1 通信星座卫星参数值

此时，星座基于区域重要度的全球覆盖率仅为79.713%，平均覆盖重数为1.899 3，完整的星座构型及受损星座覆盖情况如图7所示。

图7 完整星座构型及受损星座多重覆盖情况

3.2 重构分析

优化算法的参数设置为：初始种群数量设置为300，进化代数设置为20代，杂交因子为0.7，突变因子为0.4。

任务条件：

1) 受损通信星座须在3天时间内将基于区域重要度的全球覆盖率恢复至99%以上。

2) 为简化模型，不考虑干扰、信息截获等因素，认为通信卫星只需覆盖即可为该区域提供任务所需的通信能力。

目标函数：

minF=(C,ΔVall)

(16)

基于区域重要度的全球覆盖率C；重构所需消耗总能量ΔVall。

优化结果如图8所示。

可见，此时覆盖损失值对应区间为[0.002 068，0.202 87]，即覆盖率对应区间为[0.797 13，0.995 22]，重构所需能量对应区间为[0，0.145 04]。在满足任务条件即覆盖损失值小于1%的前提下，考虑资源消耗尽可能小，选择满足要求且距离1%最近的Pareto前沿上的坐标点。即坐标点(0.004 78，0.145 04)。此时，上层基因S=[0 0 1 0 1 0]，即3号和5号卫星参与重构。参与重构的3号卫星的真近点角重构为64.43°，其能量消耗为0.115 38 km/s ；参与重构的5号卫星的真近点角重构为188.58°，其能量消耗为0.029 66 km/s，完整的重构过程所需消耗总能量为0.145 04 km/s。当前时刻下的全球覆盖情况如图9所示，仅有少部分区域在短时间内失去通信覆盖。基于区域重要度的全球覆盖率为99.522%，即在一个回归周期内，星座能够保证全球范围内用户在99.522%的时间均可实现通信服务，基本能够保证通信任务需求。

图8 以C和ΔVall为目标函数下的Pareto前沿

图9 重构后的通信星座全球覆盖情况

4 结论

针对有卫星失效的中高轨通信星座，根据覆盖率和最小燃料消耗等优化条件，提出多个优化指标模型，并采用NSGA-Ⅱ算法进行多目标优化建模求解，提出基于同轨道面内进行轨道机动的星座重构优化方案。实验表明，当部分卫星失效时，该方法能够根据目标函数快速构建Pareto前沿，为星座重构提供最优方案解集。此外，本文的研究对象主要针对中高轨通信星座，其星座构型相对简单，对星间链路和星地传输进行了一定的简化处理。与之相比，低轨通信星座的信息传输更依赖星间链路和星地传输等传输链路的连通性，在后续的研究中，可考虑加入星间链路和星地传输等约束条件，开展低轨通信星座重构方法研究。