随机植物－食草动物模型的共存性与排斥性

张卿卿， 黄在堂， 林 怡， 张 绿， 陆桂菊

（南宁师范大学 数学与统计学院，广西 南宁530023）

植物－食草动物的相互作用一直是生态学、进化生物学和资源管理中重点研究的问题［1］．然而，大多数植物－食草动物模型没有考虑将毒素介导的浏览效应纳入植物种群动态．为了探讨植物毒性对植物－草食动物相互作用的动力学行为的影响，考虑植物毒素引起的食草动物数量的减少，从而修改传统的Holling II型功能反应，建立了毒素确定的功能反应（TDFR），称为毒素确定的功能反应模型（TDFRM）［2－3］．与以往的植物－哺乳动物相互作用模型［4－5］相比，它展现出各种复杂的动力学行为．

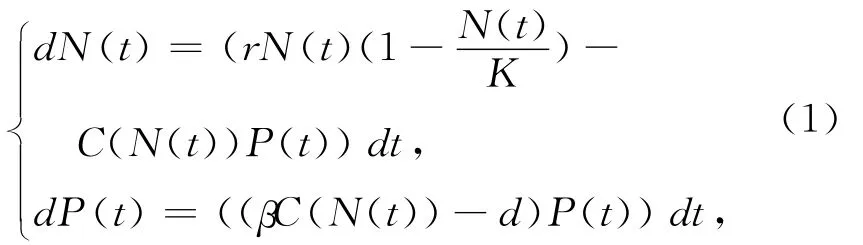
本文只考虑二维TDFRM系统，包括一种植物物种和一种食草动物群体的情形［2－3，6］，从而此系统可由以下微分方程描述其中，N（t）表示可用于食草动物的植物的生物量，P（t）表示在时间t的食草动物的生物量，毒素确定的功能反应为是HollingⅡ型功能反应，r和K 分别是植物物种的固有生长速率和承载能力，e表示每一个食草动物与每单位植物的接触率，h表示处理一单位植物生物量所需的平均时间，β表示消耗的植物生物量转化为新的食草动物生物量（通过生长和繁殖）的转化率，d为食草动物的自然病死率，常数G表示食草动物每单位时间可消耗的最大毒物量，且＜G＜．然而现实社会中，生态系统不可避免遭受环

境的影响，例如飓风、地震、流行病等因素．因此，在二维TDFRM系统引入随机因素，则模型转化为如下随机模型其中，N0＝n0＞0，P0＝p0＞0，模型中的参数都是正数，B1（t）、B2（t）和 B3（t）表示标准一维布朗运动．

本文主要研究随机植物－食草动物模型的长期性行为，引入2个阈值λ1、λ2来定义随机共存性与排斥性．首先，当λ1＞0且λ2＞0时，则发生共存，再利用指数鞅不等式、遍历理论和马尔科夫性等理论，证明了随机植物－食草动物模型存在唯一的不变概率测度，从而给出了共存性条件；其次，当λ1＜0或λ2＜0时，则发生排斥；然后，通过运用强大数定律、非常返性和Portmanteau定理等理论，给出了随机植物－食草动物模型排斥性的条件，且证明了模型正解分布的收敛性．

1 主要结论

命题1．1［7］下面这些论断成立：（i）存在M0＞0使得

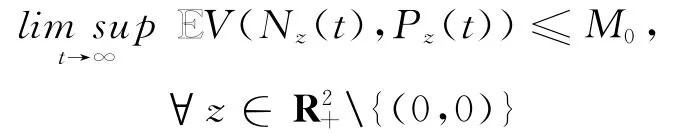
成立，其中V（n，p）＝（n＋p）－1＋（n＋p）；

（ii）对任意ε＞0，H＞1，T＞0，存在珨H＝珨H（ε，H，T）＞1，使得，当z∈［H－1，H］×［0，H］时，

成立，并且当z∈［0，H］×［H－1，H］时，

成立；

（iii）对任意θ∈（0，3），存在Mp＞0，使得

下面先考虑模型（2）N轴上的边界方程

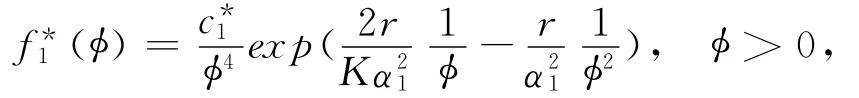
c＊1为归一化常数．根据遍历性（文献［10］中的定理3．16），对任意可测函数g（·）：R＋→R满足

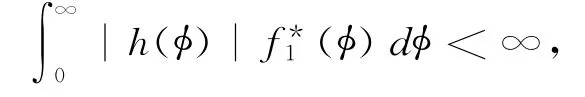
则有

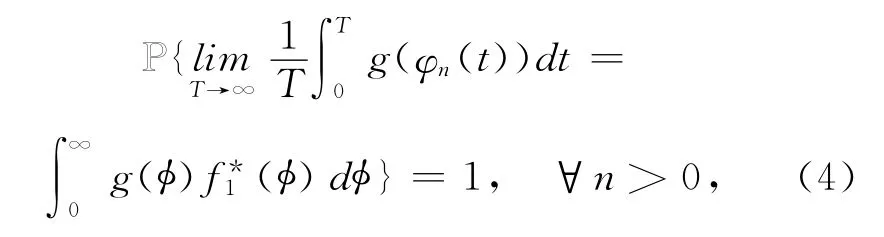
其中φn是（3）式的初始值为n的解．特别地，对任意θ∈（－∞，3），

定义

类似地，考虑该模型的另一个边界方程

该方程存在唯一不变概率测度π＊2．定义

其中f＊2（·）是π＊2的密度函数，且

下面详细说明λ1、λ2的定义和使用．为了确定Nz（t）是否收敛到0，考虑当 Nz（t）在足够长的时间内仍然很小时它的Lyapunov指数．因此，由I公式可得方程

该方程有唯一不变概率测度π＊1∈（0，∞），其密度函数为

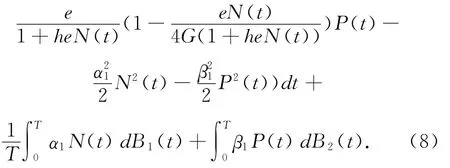
当T足够大时，（8）式右边第一项与第三项都很小．显然，如果Nz（t）在［0，T］内足够小，则Pz（t）趋近于ψp（t）．由遍历性［10］，可得趋近于λ2．下面采用文献［11］的方法给出随机共存和排斥的定理，然后说明本文的主要结果，最后给出证明．

定理1．1 如果λ1和λ2都为正数，那么2个物种共存，而且解Z（t）在R2＋上存在唯一不变测度μ＊，使得：

（i）Z（t）的转移概率P（t，z，·）在总变量中收敛于μ＊，z∈R2＋；

（ii）对于任何μ＊－可积函数F（z）：R2＋→R，有

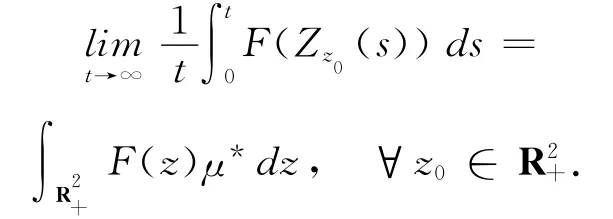
定理1．2 如果λ1＜0且λ2＞0，那么Nz0（t）的分布弱收敛于π＊1且如果λ1＞0且λ2＜0，那么Pz0（t）的分布弱收敛于π＊2且

定理1．3 假设λ1与λ2都为负数，对于任意z0∈R2＋，有uz0＞0，vz0＞0且uz0＋vz0＝1，则有：

而且Zz0（t）弱收敛于

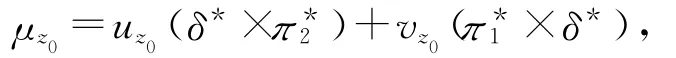
其中δ＊是收敛于0的Dirac量度．更准确地说，对于任何可测集A，BR，有

2 共存性

下面给出在证明过程中将多次用到的指数鞅不等式．对任何的a＞0，b＞0，

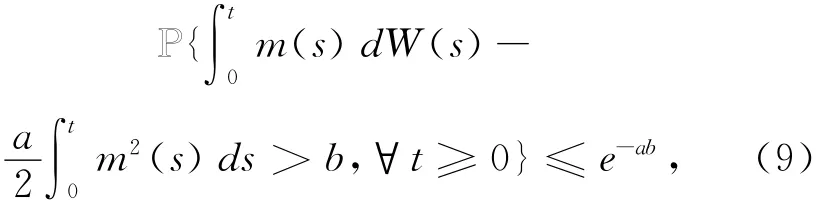
下面给出在证明过程中将多次用到的指数鞅不等式．对任何的a＞0，b＞0，如果W（t）是Ft－适应的布朗运动，m（t）是实值适应过程，那么几乎处处成立（文献［12］中的定理1．7．4）．应该指出的是在文献［12］的定理1．7．4中，不等式被表述为一个有限的间断．然而（9）式成立，由于

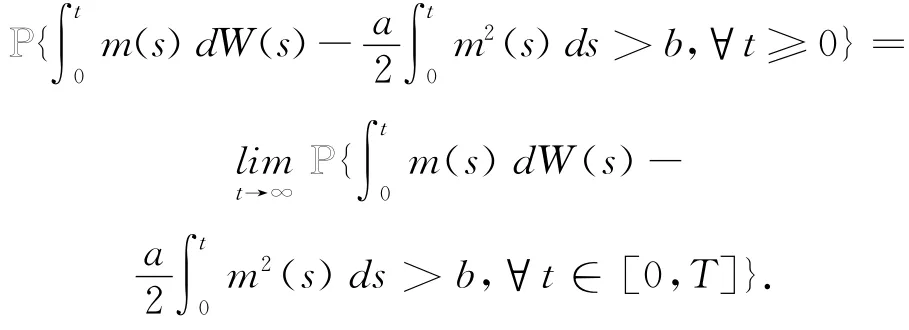
1A为集合A上的示性函数．利用命题1．1的（iii）和Holder不等式，可估计得

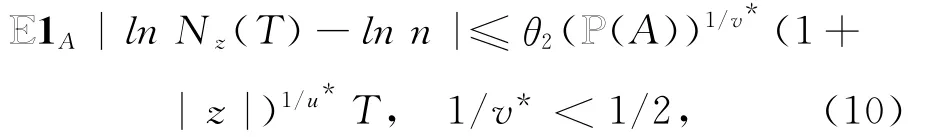
其中常数θ1、θ2与z、T、A 无关．特别地，当A＝Ω时，

所以

下面定义一停止时间

引理2．1 任取T＞1，ε＞0，σ＞0，存在一δ＝δ（T，ε，σ）＞0，使得

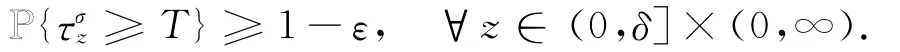
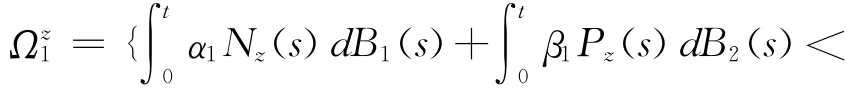
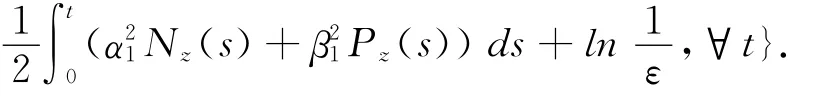
基于（8）式，当ω∈Ωz1时，有令δ＝σεe－rT，若n≤δ，则

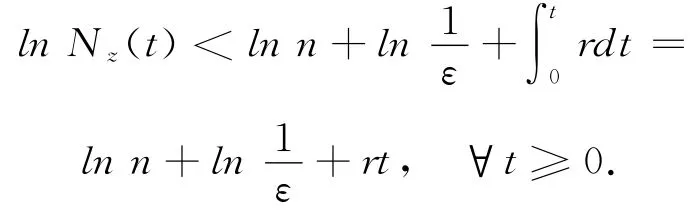
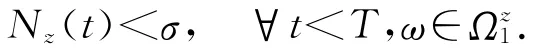
引理2．2 对任意的H＞1，T＞1，ε＞0，ν＞0，存在一σ＞0使得对所有z∈（0，σ］×［H－1，H］满足

证明 根据命题1．1的（ii），能找到一足够大的数珨H满足

令

由B－D－G不等式可得以下估计

其中m珡＝m珡（H珨，T）＞0．利用Gronwall不等式，得到

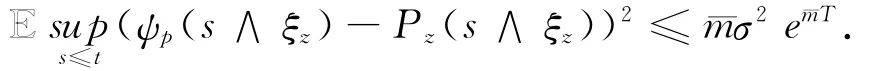
当σ足够小时，由Chebyshev不等式可得

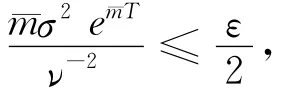
即得

结论得证．

引理2．3 对任意的ε＞0，存在＾M＞0，满足

证明 由于

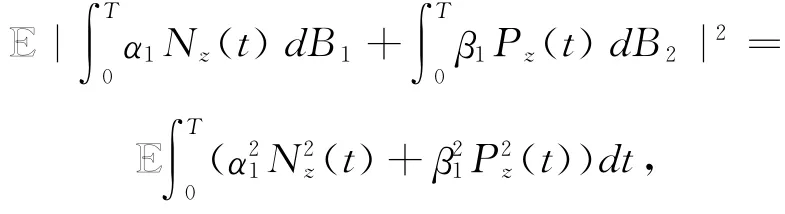
再运用命题1．1的（iii）和Chebyshev不等式可得结论．证毕．

命题2．1 假定λ2＞0，对任意ε＞0，H＞1，存在T＝T（ε，H）＞0和δ0＝δ0（ε，H），满足对任意的z∈（0，δ0］×［H－1，H］，有：

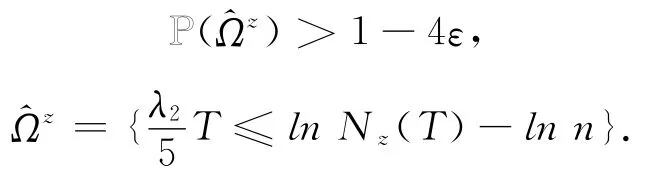
证明 由（7）式，对任意小的ν有

＾M满足引理2．3．再由ψ（t）的遍历性（见（4）式），即存在

满足

鉴于引理2．2，找到σ＝σ（ε，H）＞0使得

且

其中

根据引理2．1，存在δ0＝δ0（ε，H）对任意的］满足

其中

其中

综上，任取z∈（0，δ0］×［H－1，H］和

证明 令ε＝ε（Δ）∈（0，1），H＝H（Δ）＞1．再令Λ＝θ2（1x＋2｜H｜）1／u＊ε－1．根据（12）式的结论和命题2．1，存在δ0∈（0，1）和T＞1，使得

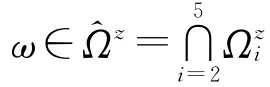
可得

命题2．2 假定λ2＞0，则对于任意Δ ＞0，存在使得

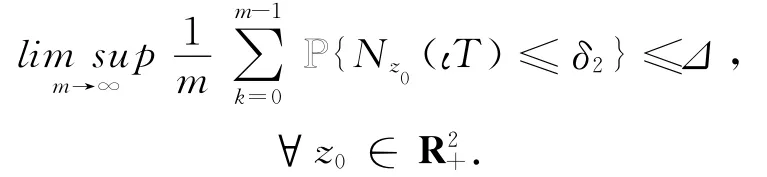
其中

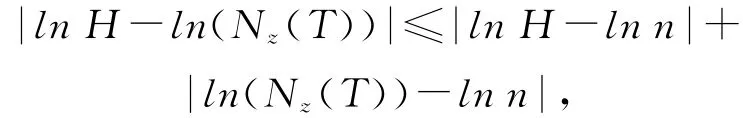
则有

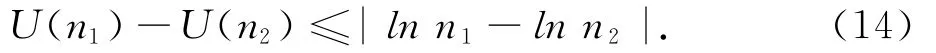
若

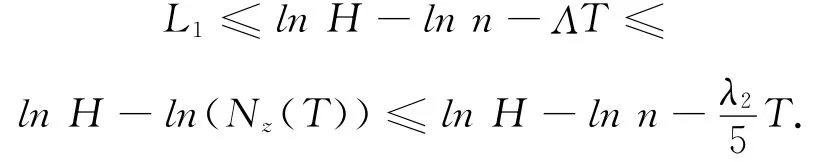
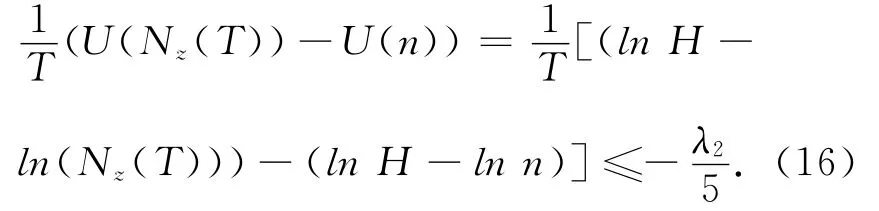
对于任意的z0∈R2＋，利用Z（t）的 Markov性质可得

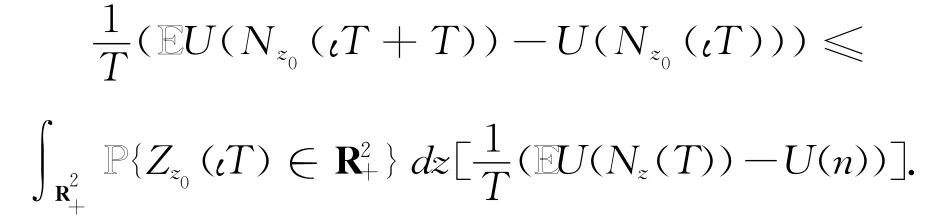
记D ∶＝［H－1，H］2＝∪3i＝0Di，由B－D－G不等式可得以下估计

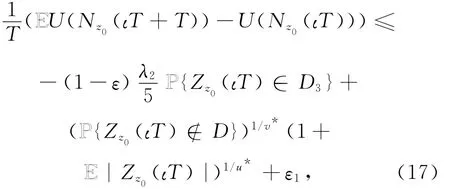
其中

再根据命题1．1的（i），有

与

显然

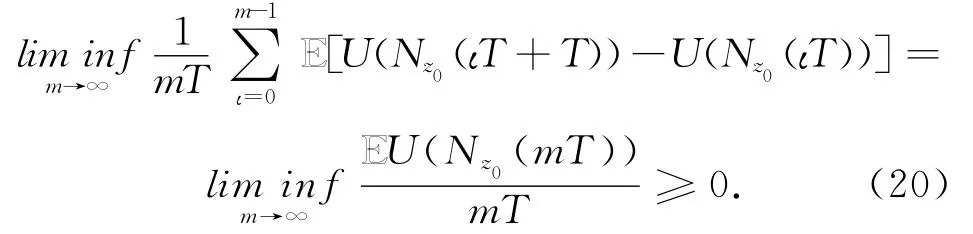
再根据（17）、（18）和（20）式可得出

注意到

再根据（19）和（21）式，只要选择足够大的 H＝H（Δ）和足够小的ε＝ε（Δ），则结论得证．

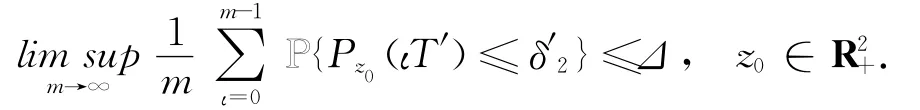
定理1．1的证明 任取ε＞0，由于λ1＞0，则类似于命题2．2，存在T′＞1和δ′2＞0使得此外，在命题2．2的证明中可以看出，可以选择足够大的T′和足够小的δ′满足上述不等式．不失一般性，令T′＝T，δ′2＝δ2，有由此不等式与命题1．1中的（i），可知存在一紧集GR2＋满足

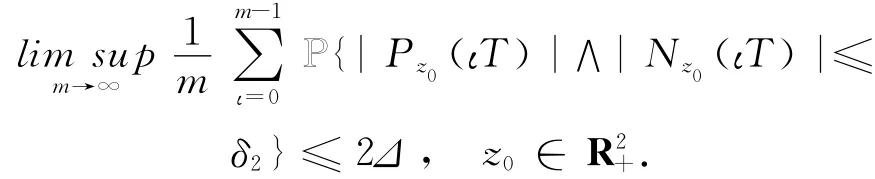
再根据命题1．1中的（ii），知存在l＞1，使得对任意的z∈G，t∈T，有

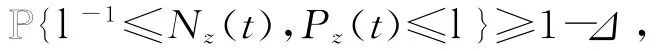
利用Markov性质得

故对任意z0∈R2＋，

即有

这意味着存在不变概率测度．定理1．1的其余结果可由模型的非退化性得证，详情可见文献［13－14］．因此定理1．1即共存性得证．

3 排斥性

为了证明定理1．1即共存性，只需要估计在足够长但有限的时间内解在边界附近的行为．相反要证明定理1．2与1．3即排斥性，需要估计在有限时间内φn（t）－Nz（t）的值．由于在确定性情况下，对于方程

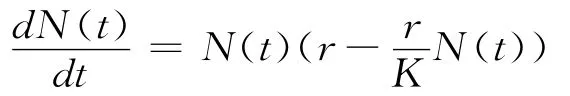
的解的逆N－1（t）满足线性微分方程，则该方程更容易处理．因此先考虑φn－1（t）－Nz－1（t）的值．

引理3．1 对任意的H＞1，T＞1，ε＞0和γ，存在σ珓＞0使得z∈［H－1，H］×（0，σ珓］有

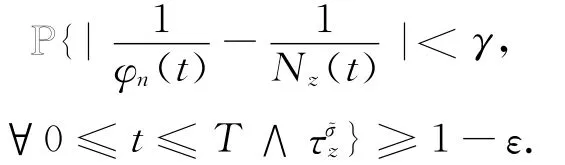
证明 根据命题1．1中的（ii），可以找到＾H＝＾H（ε，H，T）＞1对任意的z∈［H－1，H］×（0，H］有

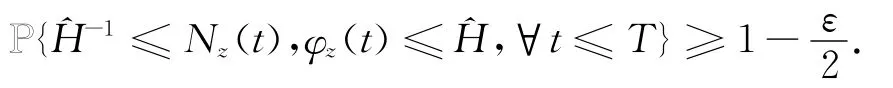
当 ＾H－1≤Nz（t），φz（t）≤＾H 时，有

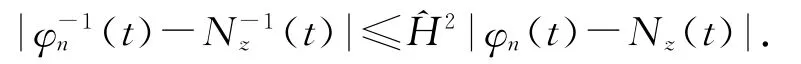
再应用引理2．2，则结论得证．

命题3．1 假定λ1＜0，对任意的 H＞1，ε＞0，

γ＞0和λ∈（0，－λ1），存在一使得

证明 考虑

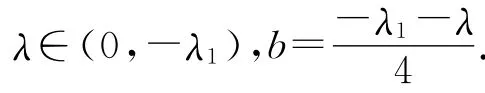
令．因为

可找到η1，η2，η3∈（0，1）有

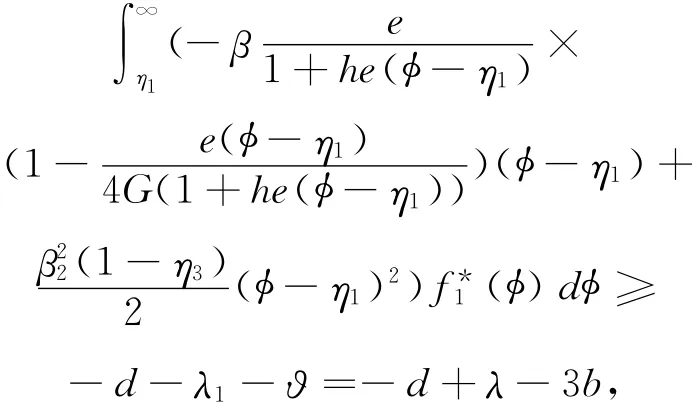
与

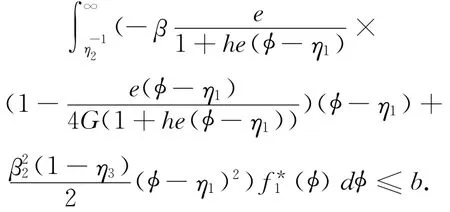
由（4）式的遍历性，存在T1＝T1（ε，H），使得其概率大于1－ε，那么有

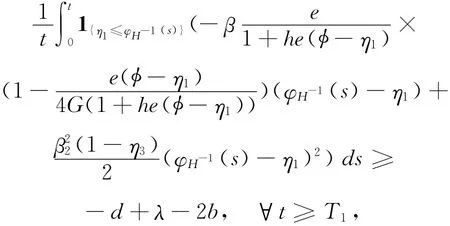
与

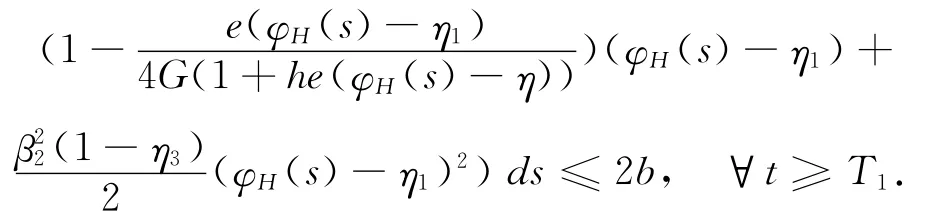
再结合φH－1（s）≤φn（s）≤φH（s）a．s．，且其概率大于1－ε，对于s≥0，n＞H－1有：

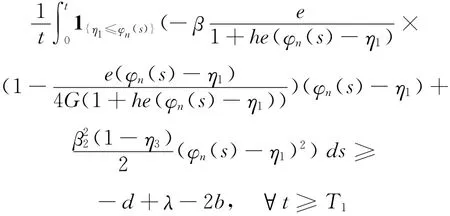
和

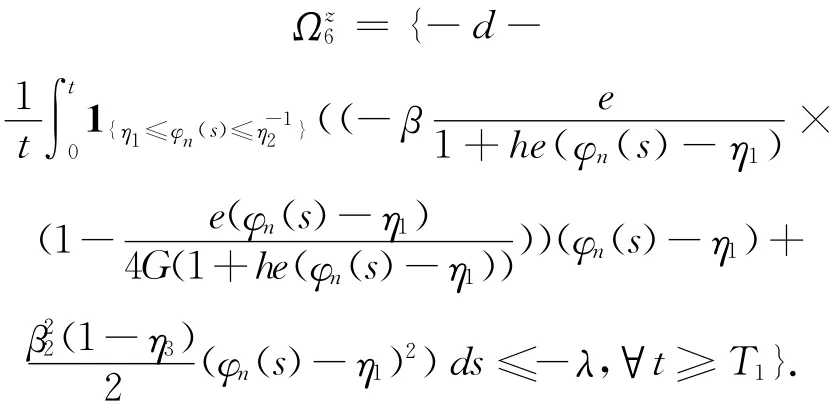
成立时，

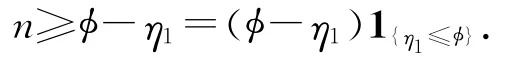
因此，当ω∈Ωz6∩z≥T1，有

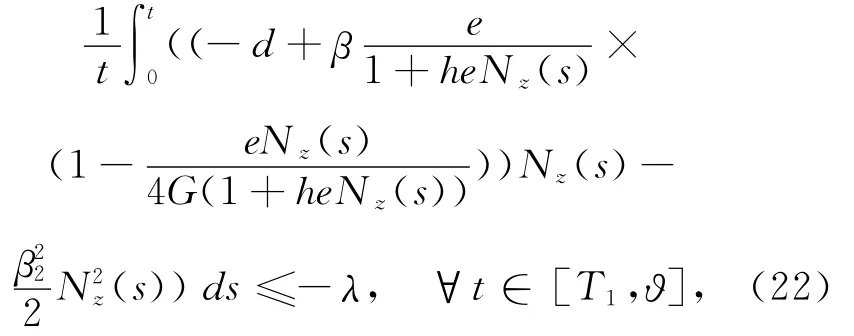
其中

又因

令

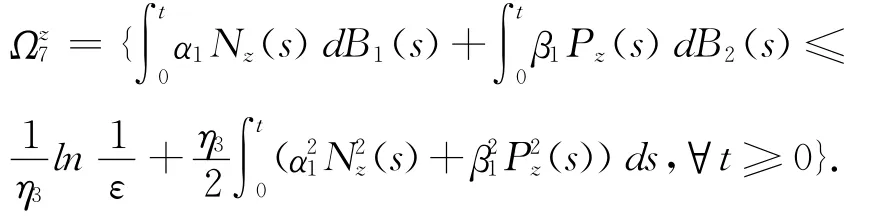
根据（22）、（23）式，则当ω∈Ωz6∩Ωz7∩｛z≥T1｝时，有

若N≤1，记

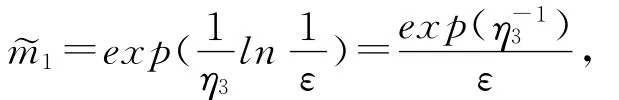
有

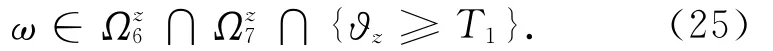
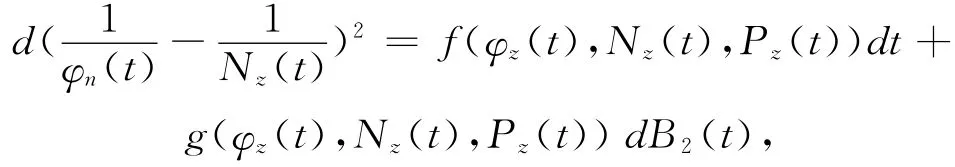
其中

且

再令

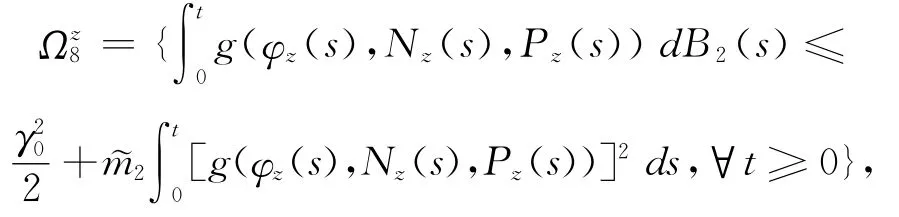
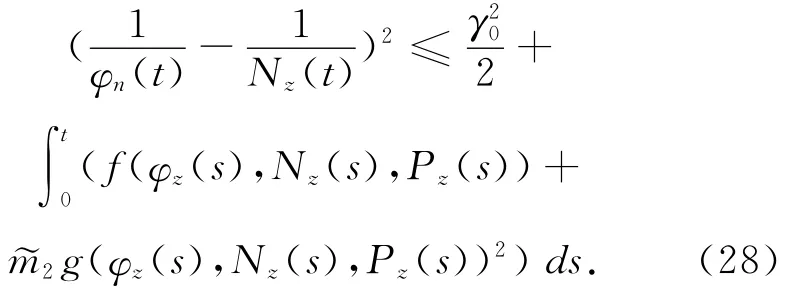
利用（26）、（27）式可得

其中

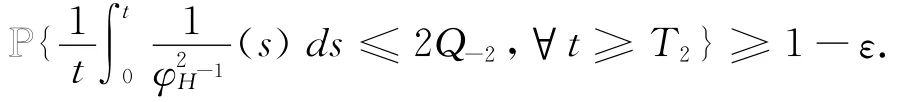
因此，对所有n∈［H－1，H］，使得

其中

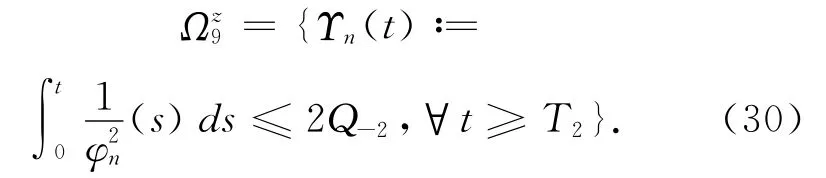
显然，可以找到一T3＝T3（ε，H）＞T1∨T2满足

取足够小的σ珓＝σ珓（ε，H）＜1，有

再根据引理2．1与3．1，找到足够小的δ珘＝δ珘（ε，H）有：

和

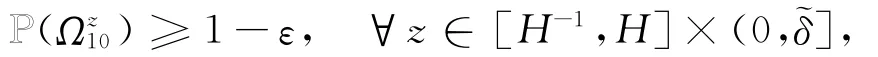
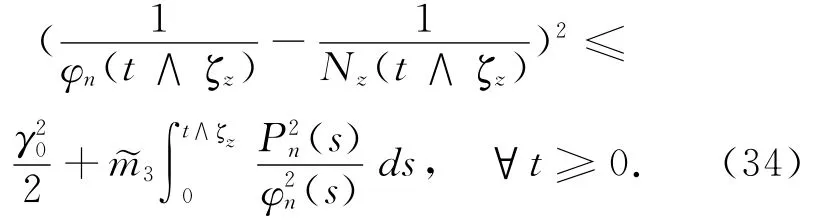
当ω∈Ω珟z时，根据（34）、（35）式，有

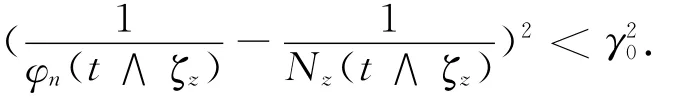
因此，在Ω珟z中有

即

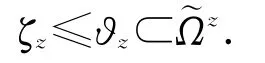
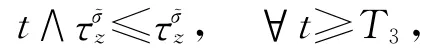
时，有

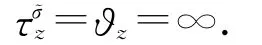
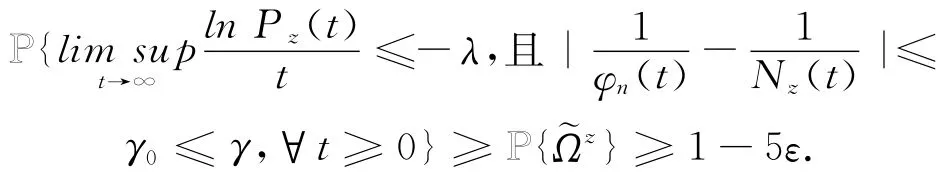
证毕．

命题3．2 对于任意的H＞1，ε＞0和ρ＞0，存在δ珔＞0使得对任意的z∈［H－1，H］×（0，δ珔），有

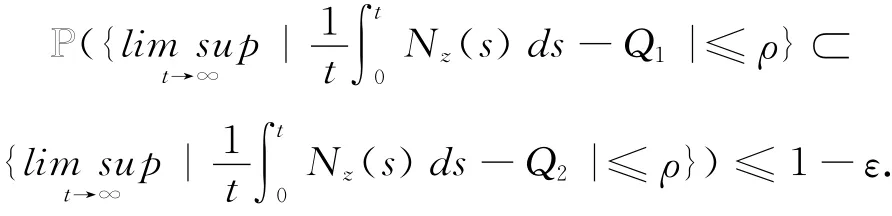
与

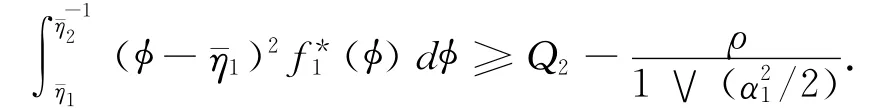
由命题3．1，存在δ珋＞0满足对所有的z∈［H－1，H］×（0，δ珔］，有

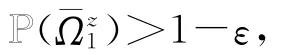
其中

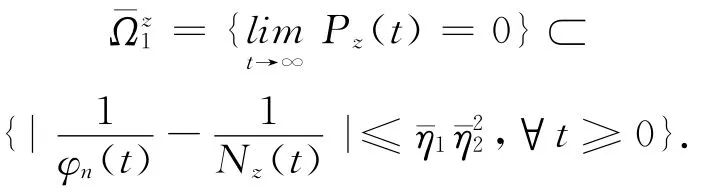
与

运用φn（t）的遍历性与鞅的强大数定理，可得下面结论

则

此再根据文献［15］中定理2．2的证明以及Pz（t）在Ω珚z1中收敛到0，可得对ω∈Ω珚z1几乎处处成立．再由（36）～（38）式可得命题，即得证．

下面证明定理1．2和1．3．

定理1．2的证明 假如λ1＜0且λ2＞0，考虑任意的ε＞0，γ＞0，λ∈（0，－λ1）．根据命题1．1，则存在H＞1，使得

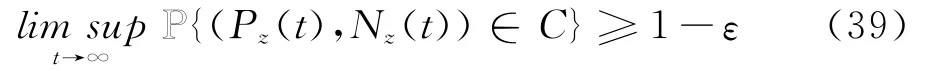
成立，这里C∶＝｛H－1≤n∨p≤H｝．类似命题3．1，存在＞0，满足当C1∶＝［H－1，H］×（0，δ珘1），

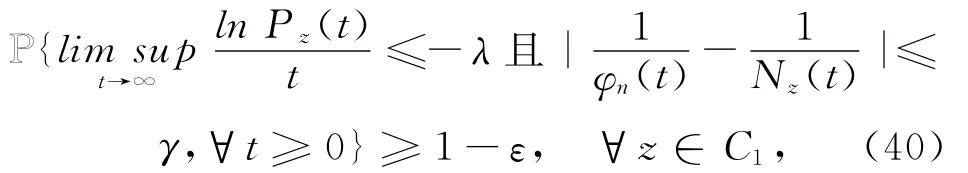
又因为λ2＞0，故类似于命题2．2，存在T4＞1，δ珘2＞0，使得

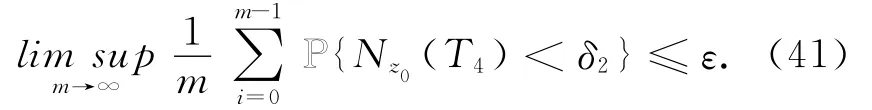
结合（39）、（41）和（42）式可得

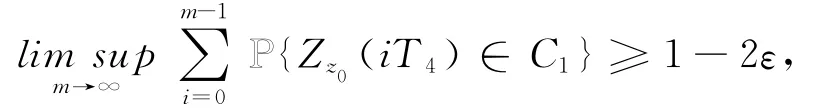
存在i0使得．由 Markov

性质与（40）式可推导出

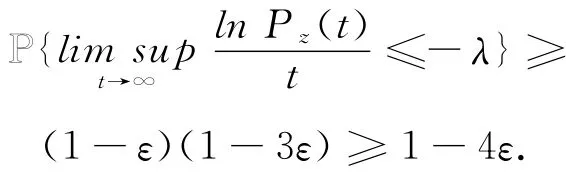
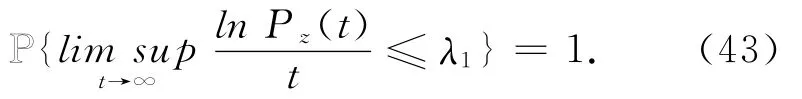
同样，利用命题3．2和上面的论点，可得到

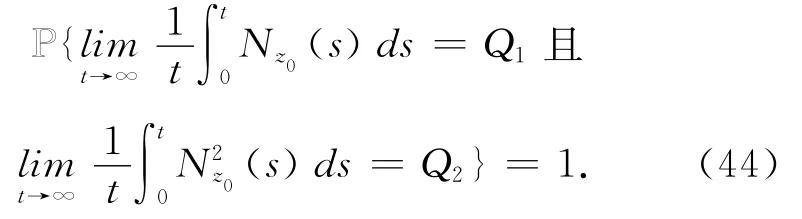
再利用鞅的强大数定理，有

将（43）～（45）式代入（8）式得

下面主要证明Nz－01（t）在（0，∞）的分布弱收敛于测度π1，其值为

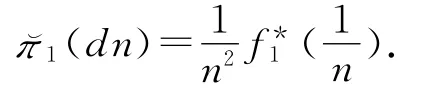
根据Portmanteau定理，令w（·）为（0，∞）上的Lipschitz函数，则有定义Xw＞0，对所有的n1，n2∈（0，∞），满足

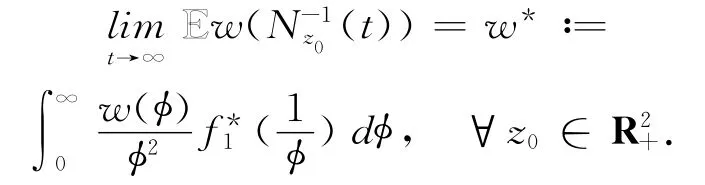
且

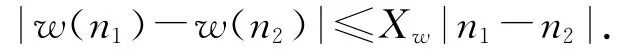
有下面的估计

根据（46）式以及φn－1（t）的分布弱收敛于π1（因为φn（t）的分布弱收敛于π1＊），得

再由Markov性质有

根据（40）、（47）式并在（48）式上应用 Fatou引理，得到

当ε＞0，γ＞0都足够小时， EE w（Nz0（t））收敛于w＊．定理1．2得证．

定理1．3的证明 对于任意ε＞0，存在H＞1有

其中

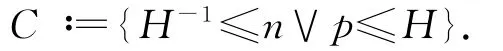
由于λ1＜0，λ2＜0，令λ′1∈（0，－λ1），λ′2∈（0，－λ2），存在δ珘3＞0满足

和

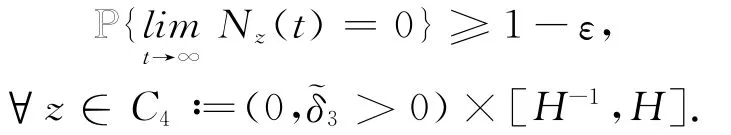
且uz0＋vz0＝1．

由于

类似于定理1．2的证明，存在一TZ0（ε）＞0，得到

剩下的部分可类似于定理2．2的证明．定理2．3得证．综上，定理1．2与定理1．3得证，即排斥性得证．