基于改进的稀疏度自适应振动数据修复方法
2019-08-31王华庆宋浏阳李景乐郝彦嵩
谢 馨, 王华庆, 宋浏阳, 李景乐, 郝彦嵩
(北京化工大学 机电工程学院,北京 100029)
旋转机械作为现代工业中重要的生产设备,一旦发生故障,将造成巨大损失。因此对旋转机械进行状态监测,从而及时发现并解决故障有重要意义[1-3]。复杂的监测环境对数据采集系统会产生一定影响。在实际振动信号采集中,可能会由于信号传输故障或设备间的电磁干扰导致部分数据的丢失。但采集过程不可逆,因此有必要对不完整数据进行修复,为后续信号处理奠定基础。
近年来在稀疏表示基础上发展的压缩感知理论为信号处理技术提供了新思路。压缩感知理论中,首先对信号进行稀疏变换,再利用与变换矩阵不相关的观测矩阵实现信号的压缩,最后通过求解欠定方程得到重构信号。它的优势在于能够通过较少的采样值保留原信号本质特征,在欠采样条件下高概率地重构信号。
基于上述原理,如果将信号采集过程得到的有损信号作为观测值,那么用有损信号恢复完整信号的过程就可以看作是压缩感知的重构过程。因此,对于缺失数据修复问题,已有文献利用相关理论开展了工作[4-6]。在压缩感知理论中,选择恰当的重构方法对精确稳定地恢复出高维信号极其重要。其中贪婪算法是最常用的稀疏求解算法[7-10],包括正交匹配追踪(Orthogonal Matching Pursuit,OMP)、正则化正交匹配追踪(Regulariged Orthogonal Matching Pursuit,ROMP)、压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)等。但以上算法均需对信号稀疏度进行预估,增加了数据重构的难度。为了解决上述问题,稀疏度自适应匹配追踪算法(Sparsity Adaptive Matching Pursuit,SAMP)被提出[11-12]。
SAMP算法每一阶段内,当搜索的支撑集原子更匹配原信号时,残余范数减小,同时更新支撑集及余量;当残余范数增大时,进入下一阶段,同时增加支撑集大小,直到满足迭代终止条件,循环终止。因此,便增大了对终止条件的依赖。若终止系数选取过大,则重构误差较大;若选取过小,则会持续增加支撑集的大小。这样不仅增加了迭代时间,而且当支撑集大小远大于真实支撑集时,还会引入大量错误原子,反而降低了重构精度。为此,本文提出了基于终止准则改进的SAMP算法,对SAMP算法的终止条件进行优化补充,使其不仅仅依赖于终止系数的选取。从而在数据修复的过程中,缩短了运行时间,同时可以自适应完成信号重构,避免了人为因素。
1 基于压缩感知的振动数据修复
压缩感知理论中,当信号在某个变换基下具有稀疏性,可以用一个与变换基不相关的观测矩阵将高维信号投影到低维空间上,再通过稀疏求解策略将低维数据重构出原始高维信号[13-15]。在数据采集过程中,由于信号传输或传感器接触不良而导致部分时间内振动数据丢失。由于这些数据的丢失是随机的,正如压缩感知理论中高维信号通过随机的观测矩阵投影在低维空间里。因此基于采集到的不完整数据,应用压缩感知重构方法,可以高概率地重构出完整信号,进而实现数据修复。
设x∈RN×1为原始完整信号,y∈RM×1为受损信号,那么二者关系可以表示为
y=Φx
(1)
式中:Φ∈RM×N(M 设原始信号能在某种正交基下展开 x=Ψα (2) 式中:Ψ={Ψ1,Ψ2,…,ΨN}∈RN×N为正交基字典矩阵;α={α1,α2,…,αN}为展开系数向量。将式(2)代入式(1)为 y=ΦΨα=Aα (3) 式中:A=ΦΨ为感知矩阵。因此,从压缩信号中恢复原始信号是一个求解线性方程组的问题。但是由于压缩信号长度远小于原始信号,该方程有无数多个解。但是如果原信号足够稀疏,就可以降低方程组中未知数的个数,实现欠定方程的求解。 目前,稀疏求解策略很多,其中贪婪算法由于其结构简单,运算量小以及重构精度较高而被广泛使用[16-17]。但是大多数贪婪算法都需要预估信号的稀疏度,稀疏度选取的不当将会直接影响重构的效果。但是在实际工程应用中,难以确定信号真实稀疏度,导致重构结果不理想。针对上述问题,SAMP算法提供了新思路。SAMP算法通过阶段步长逐步实现支撑集的筛选,因此在稀疏度未知的前提下也可实现信号的准确重构。 SAMP算法中,每一阶段内,如果残余范数大于上次迭代残余范数,则增大支撑集的大小;否则继续搜索更优支撑集,直到满足停止迭代条件时,退出循环,此时便得到与目标信号最匹配的原子。具体步骤如下: 步骤1已知感知矩阵A、观测向量y,设置迭代终止条件,迭代步长l; 步骤2初始残差r0=y,初始支撑集I0=[ ],初始阶段s=1,初始迭代次数k=1,初始支撑集长度h=l; 步骤3求取感知矩阵A各原子Ai与余量rk-1内积〈Ai·rk-1〉,由高到低,选取h个内积最大对应的原子进入预选集Ck; 步骤4合并预选集Ck与原支撑集Ik-1得到候选集Jk,再计算候选集Jk中各原子与残差内积,选取内积最大对应的h列原子进入支撑集Ik; 步骤5更新支撑集Ik,更新残差rk。至此,一次迭代完成。若‖rk‖≤σ×‖y‖,则终止迭代,利用支撑集中原子重构信号;否则进入步骤6; 步骤6若‖rk‖<‖rk-1‖,更新迭代次数k=k+1,转步骤3;否则,更新迭代阶段s=s+1,更新支撑集长度h=s×l,转步骤3。 其中,Ck,Jk,Ik分别为第k次迭代的预选集,候选集,支撑集。 在SAMP算法中,终止系数σ的选取通常是固定的。为了重构结果更精确,终止系数σ设为0.1,或者更小。但由于字典矩阵与信号存在一定的差异,即使将支撑集长度扩展到接近观测值时,也难以满足‖rk‖≤σ×‖y‖条件,反而还会引入大量错误原子,降低了重构精度。 针对SAMP算法重构结果极大依赖于终止条件的问题,对其迭代终止条件进行了优化改进。首先利用SAMP算法对支撑集大小得到粗估计Im,使其逼近于真实支撑集的大小。后续继续搜索原子时,若新进入的原子更能准确表示原信号时,则残余范数减小‖rm+1‖<‖rm‖;若‖rm+1‖=‖rm‖,则对于当前支撑集的大小,已经搜索到了最优原子,因此需要进一步增大支撑集的大小;若‖rm+1‖>‖rm‖,说明已经引入了错误的原子,则循环终止。具体步骤如下: 步骤1已知感知矩阵A,观测向量y,迭代步长l,残差rm,支撑集Im,阶段sm,迭代次数m,支撑集长度hm; 步骤2计算感知矩阵A各原子Ai与余量rm内积〈Ai·rm〉,由高到低,选取hm个内积最大对应的原子进入预选集Ck; 步骤3合并预选集Ck与原支撑集Im得到候选集Jk,再计算候选集Jk中各原子与残差内积,选取内积最大对应的hm列原子进入支撑集Im+1; 步骤4更新支撑集Im+1,更新残差rm+1。若‖rm+1‖≤σ×‖y‖,则退出循环,利用支撑集Im中原子重构信号;否则进入步骤5; 步骤5若‖rm+1‖<‖rm‖,更新迭代次数m=m+1,转步骤2;若‖rm+1‖=‖rm‖,更新迭代阶段s=sm+1更新支撑集长度h=s×l,转步骤2;否则,退出循环,利用支撑集Im中原子重构信号。 改进后的SAMP算法不仅保证了信号的重构精度,也考虑到了在搜索支撑集的不同阶段,单一的终止条件难以有效地实现信号自适应重构;同时缩短了传统SAMP算法由于终止系数选取不当的迭代时间。 针对信号采集中受损数据的修复问题,基于压缩感知框架,提出了改进的稀疏度自适应数据修复方法。首先根据受损数据的振动特征结合先验知识确定稀疏矩阵;然后构造数据缺失模型约束下的观测矩阵;最后在重构阶段提出来一种改进的稀疏度自适应匹配追踪算法实现受损数据修复。算法流程如图1所示。 具体算法流程主要包含下述几个步骤: 步骤1采集转子实验台的轴承振动信号,以单位矩阵为基础,构造数据缺失模型下的观测矩阵,选取能够将信号稀疏化的字典矩阵作为稀疏矩阵; 步骤2在数据修复初始阶段,采用SAMP算法对支撑集进行初步估计,直到迭代次数增加,重构精度相对稳定,再利用改进的SAMP算法进行受损数据自适应精确修复; 步骤3对比受损信号与修复后信号的频谱,验证数据修复方法的有效性,分别采用OMP,ROMP方法修复信号,从修复精度和时间上与本文方法进行对比。 图1 受损数据修复流程图Fig.1 The process of mission data recovery method 为了验证方法有效性,构造了密集多模态信号x(t)如式(4)所示,其由三阶密集模态信号和随机噪声干扰xn(t)复合构成 式中:三阶模态信号幅值Ai分别为1,2,4;各阶模态信号对应频率fi分别为100 Hz,106 Hz,120 Hz;各阶模态阻尼系数ζi分别为0.010,0.006,0.006;采样频率为2 000 Hz;xn(t)为信噪比为5 dB的随机噪声。为了保证信号幅值处于同一数量级,下列信号均经过归一化处理。 完整的仿真信号及其频谱如图2所示,设在数据采集过程中由于某些外界原因造成部分数据丢失,采集到的受损信号如图3(a)所示。对受损信号进行频谱分析,如图3(b)所示,从图3(b)可知,频谱中出现了部分干扰成分,有效频率无法准确提取。因此,采用基于终止准则改进的稀疏度自适应数据修复方法恢复信号。利用改进的SAMP算法,通过受损信号、感知矩阵重构完整信号,实现数据修复。修复结果如图4(a)所示。对修复后的信号进行频谱分析,分析结果如图4(b)所示。频谱中可以有效提取各阶模态信号对应频率。 图2 完整仿真信号Fig.2 Complete simulation signal 图3 受损仿真信号Fig.3 Damaged simulation signal 图4 改进SAMP算法修复的仿真信号Fig.4 Recovery simulation signal with modified SAMP algorithm 分析了传统SAMP算法及改进的SAMP算法中,不同迭代终止系数对修复性能的影响,结果如图5所示。对于传统SAMP算法,随着迭代终止系数σ的减小,修复误差呈现先减后增的趋势。由于传统SAMP算法本身不收敛,因此难以得到全局最优解。基于终止准则改进的SAMP算法迭代终止条件不局限于单一的终止系数,还考虑了支撑集中是否引入虚假原子,并通过此次迭代余量与上一次迭代余量的相对大小进行约束。因此随着迭代终止系数的减小,改进后的SAMP算法修复误差保持稳定,即使终止系数选取过小,该算法也能自适应的精确修复,避免了终止系数选取不当对修复精度的影响。对仿真信号加入不同强度的噪声,探讨了噪声强度对支撑集原子的影响,结果如图6所示。随着信噪比减小,噪声能量逐渐高于信号能量,加噪信号包含更多不确定成分,导致数据修复搜索到的支撑集原子数也随之增加。 将本文方法与SAMP,OMP,ROMP算法进行了对比,重构结果如图7所示。本文分别从重构精度和运算时间两方面分析了改进后的SAMP与传统SAMP算法性能。从表1可知,对于修复同等长度的信号,改进的SAMP算法重构误差及运算时间均优于传统SAMP算法,这是由于改进的SAMP算法可以自适应的精确接近真实支撑集,避免σ选取不当的问题,提高重构精度和运算效率。OMP及ROMP算法修复误差如表2所示。从表2可知,改进后的SAMP算法在修复精度上高于上述两种方法,且省去了多次重复实验预估稀疏度的过程,减少了人为因素。 表2 不同重构算法修复误差 图5 迭代终止系数对修复性能影响Fig.5 Recovery error of different termination coefficient 图6 噪声对支撑集长度影响Fig.6 The length of support set under different noise intensity 图7 不同重构算法修复的仿真信号Fig.7 Recovery simulation signal with different algorithms 为验证方法有效性,在图8转子实验台上,开展了轴承振动信号采集。实验中存在轴承内圈故障及转子不对中故障,在轴承座竖直方向安装压电式加速度传感器,采集振动信号。主轴转速1 300 r/min,采样频率100 kHz,计算得该轴承内圈故障特征频率145.45 Hz。 图8 转子实验台Fig.8 Rotor experimental rig 图9为1 300 r/min内圈故障轴承振动信号经过归一化处理后的时域图及包络频谱图,从频谱中可以有效提取出轴承内圈故障频率及转频的二倍频,验证了轴承内圈故障及转子不对中故障。图10(a)为丢失部分数据后的有损信号。对有损信号进行包络解调及频谱分析,如图10(b)所示。难以有效提取轴承故障特征频率及转频的二倍频。如果不对有损数据进行修复,直接对其进行分析,将导致故障状态无法识别。 采用改进的SAMP算法修复有损信号,修复结果如图11(a)所示。同样对修复后信号进行包络谱分析,可以有效提取出轴承内圈故障频率及转频的二倍频,及初步判定轴承内圈故障及转子不对中故障,如图11(b)所示。分别采用传统SAMP,OMP,ROMP算法修复受损信号,三种方法重构结果如图12所示。本文从重构精度和运算时间两方面分析传统SAMP及本文改进后SAMP重构算法性能,结果如表3所示。从表3中可以看出,改进的SAMP算法重构误差及运算效率较传统算法均有所提升,更适于振动信号修复。OMP及ROMP方法修复精度如表4所示。可得出与仿真信号同样结论。 表3 SAMP及改进算法性能对比 表4 不同重构算法修复误差 图9 完整轴承信号Fig.9 Complete bearing signal 图10 受损轴承信号Fig.10 Damaged bearing signal 图11 改进SAMP算法修复的轴承信号Fig.11 Recovery bearing signal with modified SAMP algorithm 图12 不同重构算法修复的轴承信号Fig.12 Recovery bearing signal with different algorithms 为解决信号采集中受损数据的修复问题,提出了基于终止准则改进的稀疏度自适应数据修复方法。 (1)将SAMP算法终止准则进行优化改进,可以有效克服原方法终止条件选取的盲目性,提高了重构精度及运算效率。 (2)首先以单位矩阵为基础,构造与数据缺失模型相对应的观测矩阵。其次根据修复信号特点,选择合适的字典矩阵作为稀疏矩阵。最后利用改进的SAMP算法自适应地重构出完整信号,实现受损数据的修复。 (3)改进后SAMP算法在重构精度及运算效率上均优于传统算法,可以更好地实现未知稀疏度信号的修复。相比于OMP及ROMP算法,该方法无需多次实验估算稀疏度,自适应性强,且修复信号更有利于后续故障诊断。2 基于改进的稀疏度自适应振动数据修复
2.1 SAMP算法
2.2 基于终止准则改进的SAMP算法
2.3 数据修复模型建立
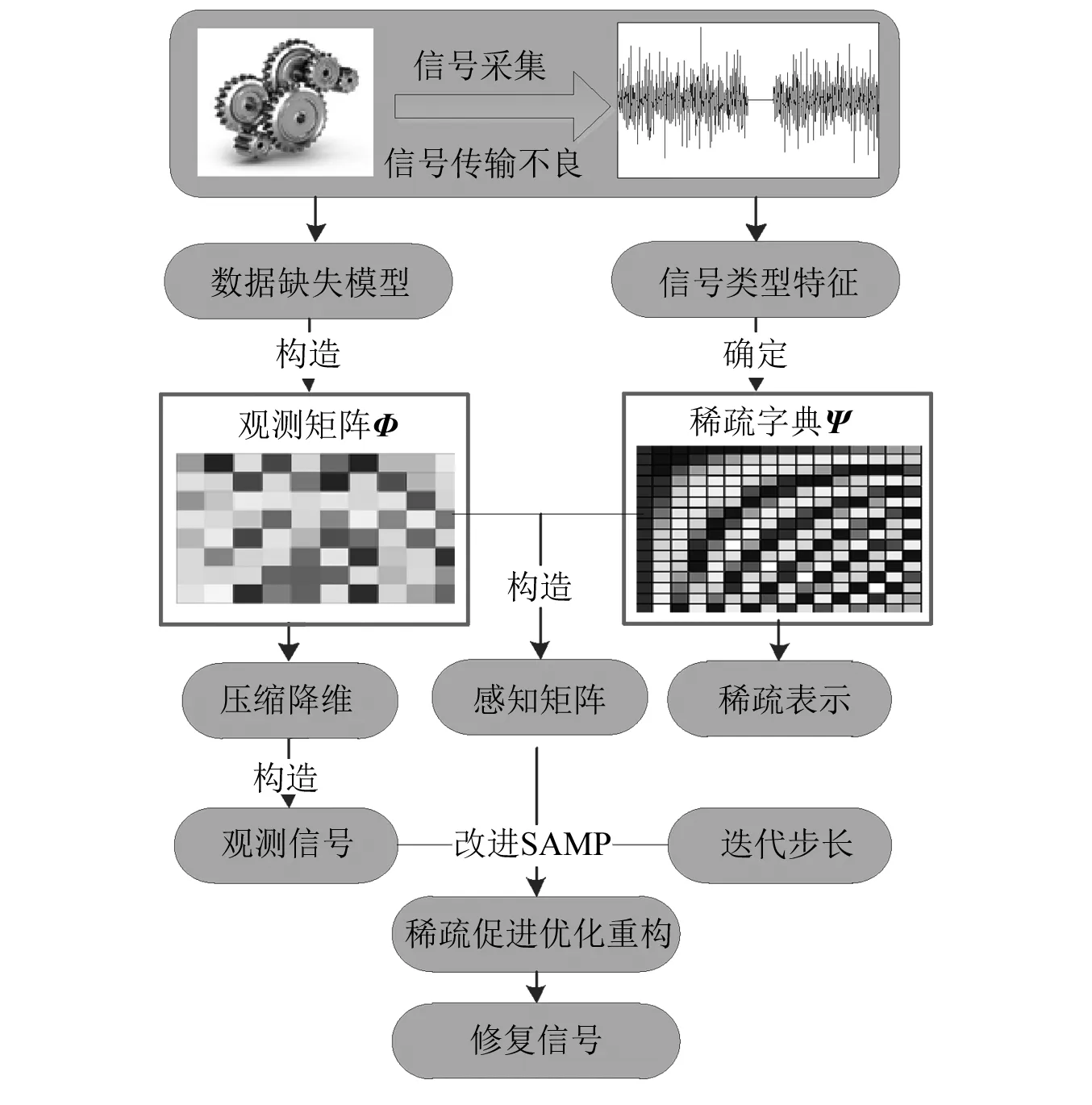
3 仿真信号验证
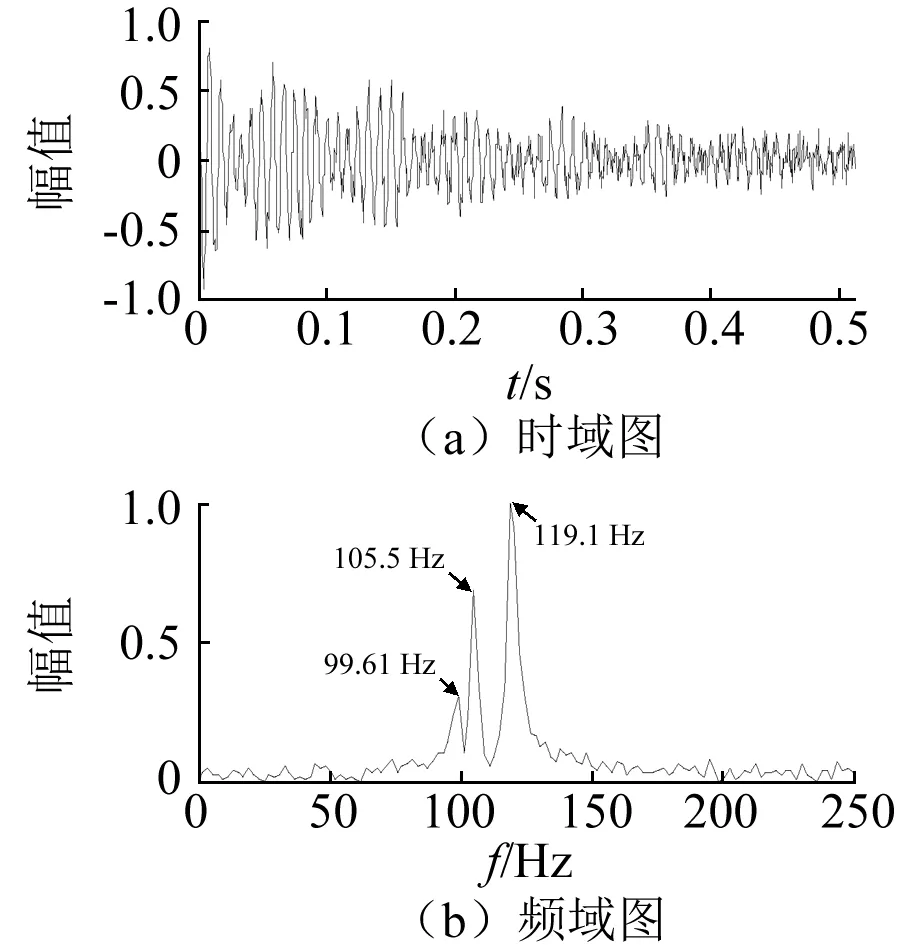

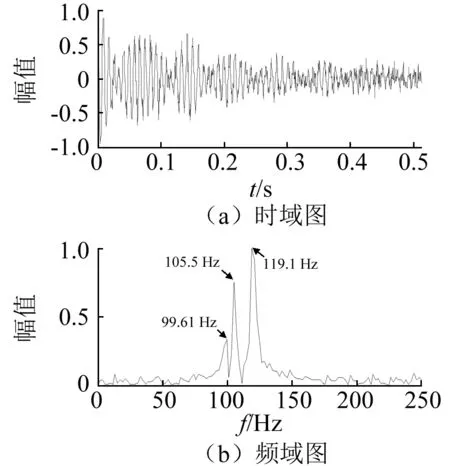




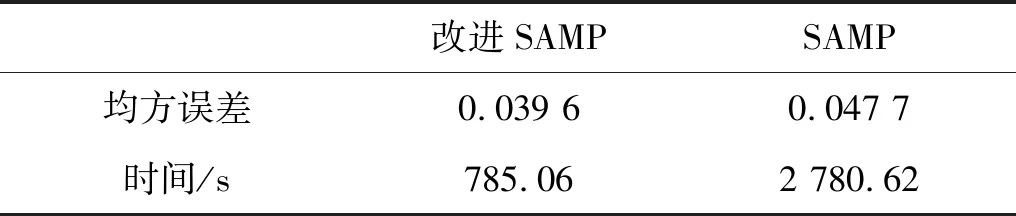
4 实验验证
4.1 实验条件

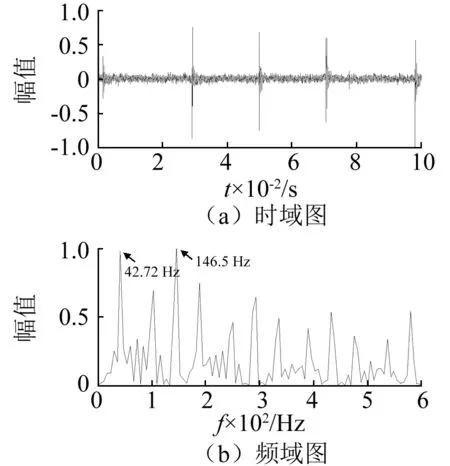
4.2 实验结果




5 结 论
