考虑主子结构动力相互作用的变电站抗震性能分析

2019-08-31牛荻涛

振动与冲击 2019年16期

文波，张路，牛荻涛，苏丽

(1.西安建筑科技大学西部绿色建筑国家重点实验室，西安 710055；2.西安建筑科技大学土木工程学院，西安 710055)

变电站作为供电系统的主要组成部分，一旦遭到破坏不但导致供电系统无法正常工作，而且使整个电力系统的运行中断，从而影响人民的正常生活，给国民经济带来重大的影响。其中，地震灾害不仅使变电站主厂房结构损坏，而且导致电气设备发生故障，使整个电力系统瘫痪。如2008年汶川大地震，在陕西、甘肃、四川三省，258座110 kV变电站发生了破坏[1-2]；2013年芦山县大地震造成了24座变电站结构不同程度的破坏[3]。

随着社会的发展，电力系统结构形式趋于多样化。然而我国对变电站结构抗震性能的理论研究还比较滞后。变电站结构设计时将电气设备作为结构层的堆聚荷载，但由于电气设备质量大、形式复杂和布局多样，现行设计方法导致目前变电站结构设计的可靠度较低且安全性较差。

目前模拟地震作用的振动台试验技术趋于成熟，国内外进行了大量的关于结构和设备的振动台试验[4-7]。谢强等[8-9]进行220 kVA/10 kV电力变压器的振动台试验，初步研究变压器的位移、加速度和应变等，得出在地震作用下变压器试验数据和分析结果。Wen等[10-12]基于IEEE693标准进行振动台试验研究，得出高压设备的最大抗震承载力。但是复杂体型和大质量的电气设备与结构之间存在复杂的相互作用，因此分别研究两者的动力特性的试验结果可靠度较低。李杰等[13]进行了存在简单设备的工业建筑振动台试验，由于力学模型过于简单抽象，不能适用于具有复杂动力特性的工业建筑。因而本文基于主-子结构动力相互作用机理建立三维有限元模型，然后根据振动台模拟地震作用试验，通过对比试验结果和数值模拟分析结果得出考虑主子结构动力相互作用的结构体系的整体抗震性能。本文成果对类似生命线工程和带有复杂设备的工业建筑抗震设计具有指导作用并完善相关的抗震设计规范。

1 主-子结构动力相互作用机理

地震作用下变电站结构体系动力反应方程为

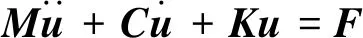
(1)

变电站结构体系包括电气设备、连接部件和主厂房结构三部分(下标表示为s，c，j)。将动力反应方程展开则为

(2)

利用Newton’s method求解上式近似解。

FN(uM)=0

(3)

(4)

(5)

2 振动台试验研究

2.1 变电站原型结构

试验原型为比较典型的一种户内式变电站结构，主厂房为三层五跨的现浇钢筋混凝土框架结构。结构平面尺寸为30 m×12 m，柱间距为6 m，框架柱截面尺寸边柱为600 mm×600 mm，中柱为500 mm×500 mm；主梁截面尺寸300 mm×700 mm，300 mm×1 000 mm，300 mm×900 mm；次梁截面尺寸250 mm×600 mm。楼层楼面板厚为160 mm，结构平面见图1。结构选用C30混凝土，纵筋和箍筋为HRB400钢筋。

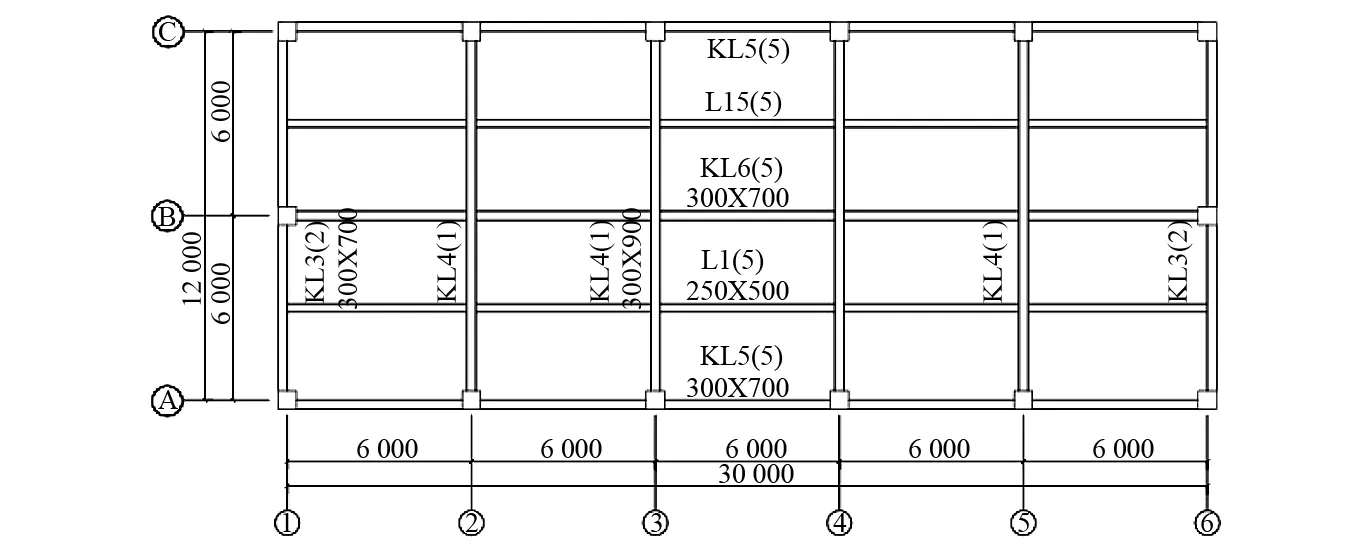
图1 原型结构平面图Fig.1 Plane of the prototype structure

电气设备采用110 kV GIS设备，尺寸为6.0 m×2.0 m×3.5 m，共7组(2组套管进出线间隔设备、5组标准间隔设备)，位于结构三层。套管进出线间隔设备立面图和标准间隔设备立面图，如图2所示。

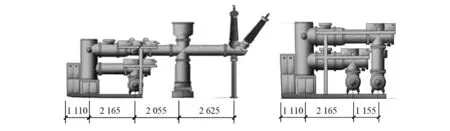
图2 设备立面图Fig.2 Elevation of the equipment

2.2 变电站模型结构

2.2.1 试验模型制作

试验模型为三层五跨的现浇钢筋混凝土框架结构，尺寸是原型变电站结构的1/8。结构模型平面尺寸为3 750 mm×1 500 mm，柱间距为750 mm，框架柱截面尺寸边柱为75 mm×75 mm，中柱为63 mm×63 mm；主梁截面尺寸38 mm×88 mm，38 mm×125 mm，38 mm×113 mm；次梁截面尺寸31 mm×75 mm。底层楼板、二层楼板及屋面层楼板厚为20 mm；一层层高310 mm，二层层高630 mm，三层层高820 mm，模型结构总高度1 760 mm。

电气设备模型包括套管进出线间隔设备和标准间隔设备，均放置于主厂房结构的三层，平面布置如图3所示。其中套管进出线间隔设备位于两端其余为标准间隔设备。

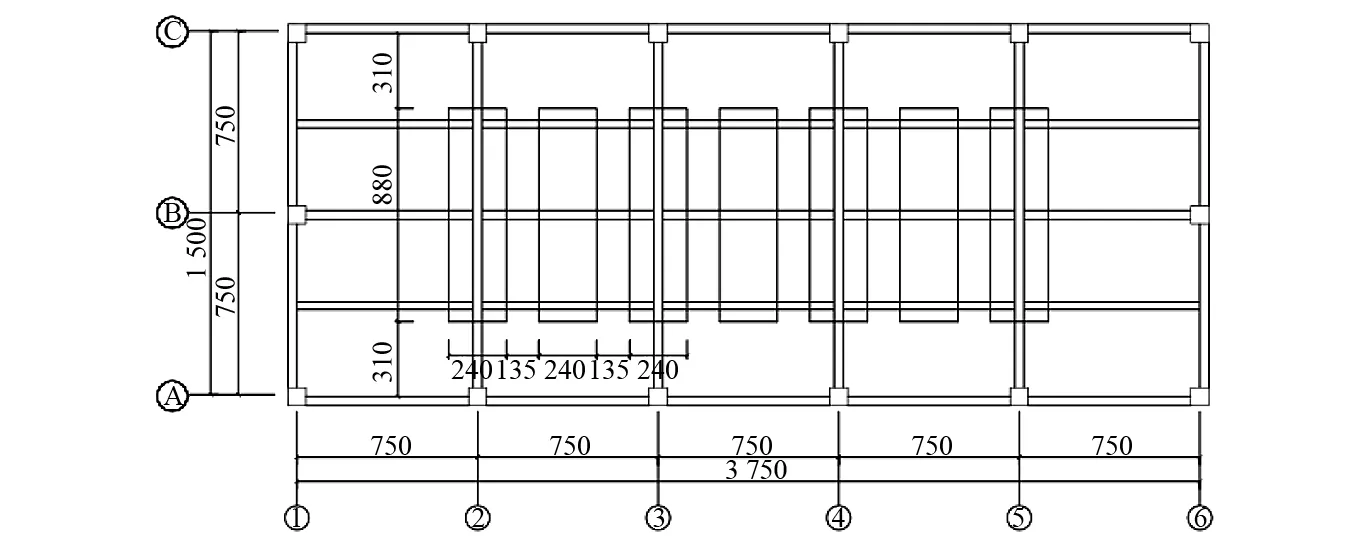
图3 模型平面布置图Fig.3 Plane of the model

2.2.2 模型相似比关系设计

试验采用三维六自由度地震模拟振动台实验系统，主要性能参数如下。台面尺寸大小为4 m×4 m，满负荷下的最大载重质量为20 t，试件最大偏心距≥0.6 m，试验频率为0.1～50 Hz。振动台最大位移：水平X向±15 cm、水平Y向±25 cm、竖向±10 cm；最大速度：水平X向±100 cm/s、水平Y向±125 cm/s、竖向±80 cm/s；载荷20 t时最大加速度：水平X向±1.5g、水平Y向和竖向±1.0g。最大倾覆弯矩80 t·m，最大偏心弯矩30 t·m。振动台试验在满足结构动力基本方程时，根据量纲协调原理，密度、弹性模量、长度和加速度相似系数满足式(6)。

Sp=SE/SLSq

(6)

综合考虑振动台性能参数和施工条件等因素，首先确定模型结构几何相似常数Sl=1/8；由试验室可以实现的混凝土强度关系确定了应力相似常数，然后根据微粒混凝土强度和弹性模量实测值、镀锌铁丝强度和弹性模量实测值再对相似关系进行调整，即应力相似常数取Sσ=SE=0.89；考虑到振动台噪声、台面承载力和振动台性能参数等因素，确定了结构和设备加速度相似系数均取Sa=2.5；由式(6)求得Sρ=2.83，模型主要相似系数见表1。

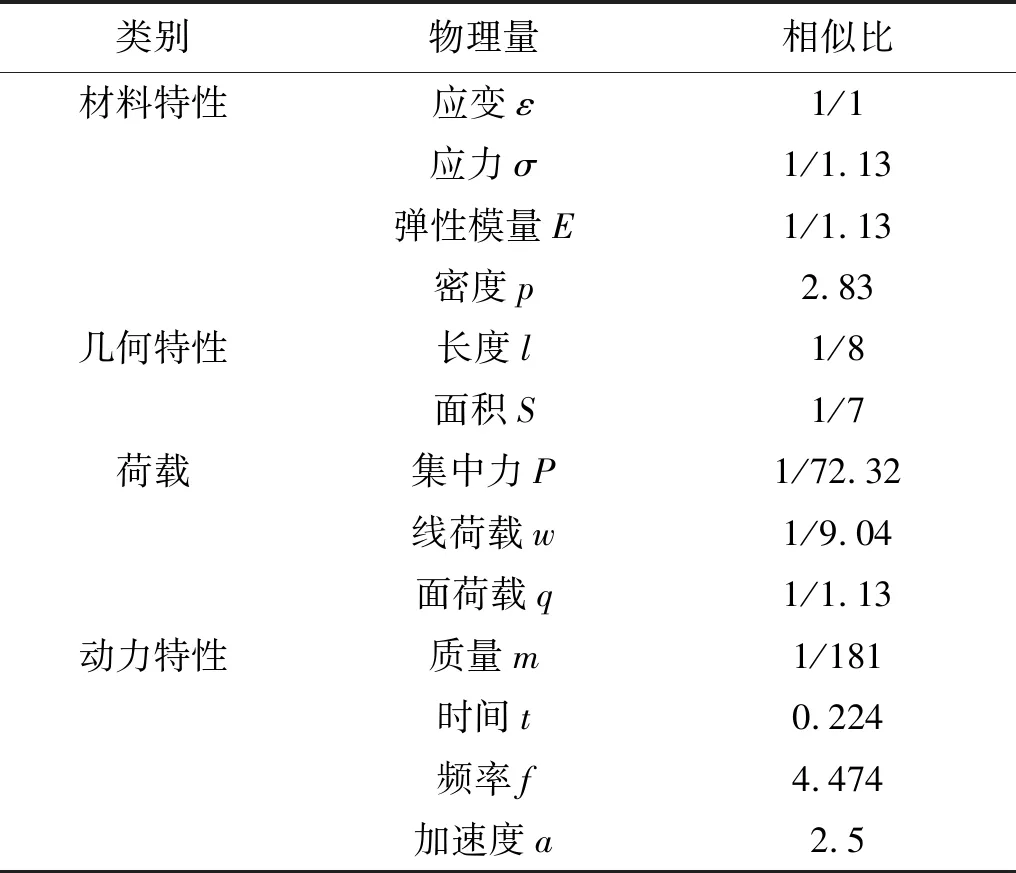
表1 试验模型的相似关系

2.2.3 模型施工

根据模型相似关系，选用微粒混凝土模拟原型结构的混凝土，铁丝模拟结构的钢筋；钢管模拟隔离开关、断路器和互感器，有机玻璃管模拟电气设备套管；将设备与楼板的连接是采用多个螺栓固定连接在三层楼板的预埋件上。浇筑每层模型结构混凝土时制作棱柱体试块并对同条件养护的试块进行材料性能试验，以调整模型结构的相似关系。

模型主体结构总质量为1.88 t，模型设备总质量为0.4 t。已知模型几何相似比Sl=1/8，质量相似比Sm=1/181，模型的构件质量为969/512=1.893 t，模型理论上质量是1 520/181=8.4 t，因此模型的配质量约为6.5 t。因而对配重按比例进行调整，模型配置如表2所示。模型施工图见图4和图5。

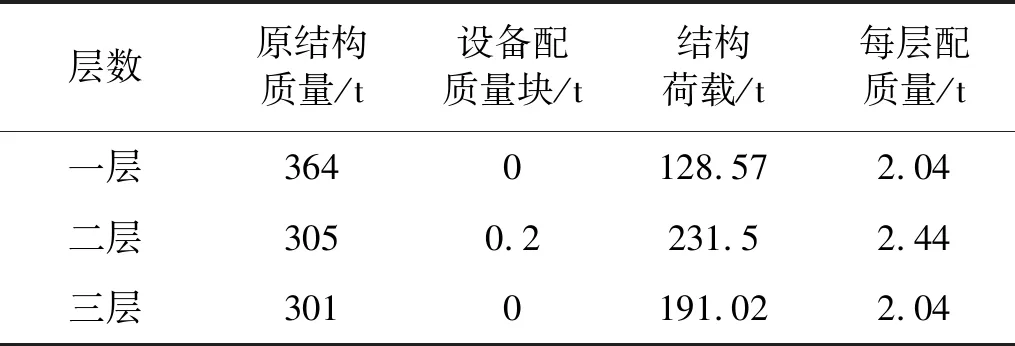
表2 模型配质量分布

图4 结构施工图Fig.4 Model construction

图5 电气设备施工图Fig.5 Equipment construction

2.3 模型试验加载制度

根据试验模型初步模拟分析和测定主子结构相互作用的抗震性能试验目的，试验加载工况按7度(0.035g)多遇(Y向、X向、XY向)、8度(0.07g)多遇(Y向、X向、XY向)、9度(0.14g)多遇(Y向、X向、XY向)、7度(0.22g)罕遇(Y向、X向、XY向)、8度(0.4g)罕遇(Y向、X向、XY向)、9度(0.62g)罕遇(Y向、X向、XY向)顺序模拟地震作用。在地震波输入前后对结构进行白噪声扫频操作，测试结构自振频率及阻尼比等动力特性参数。综合考虑结构的场地类别、自振周期和规范反应谱等要求，输入地震波选用美国加州El-Centro波、2008年汶川地震中的广元波和江油波。在同一地震幅值下由台面依次输入EL-Centro波、广元波及江油波。根据地震波的相似关系，加速度相似比取为2.5，时间相似比为 0.224。地震动加速度时程曲线如图6所示。

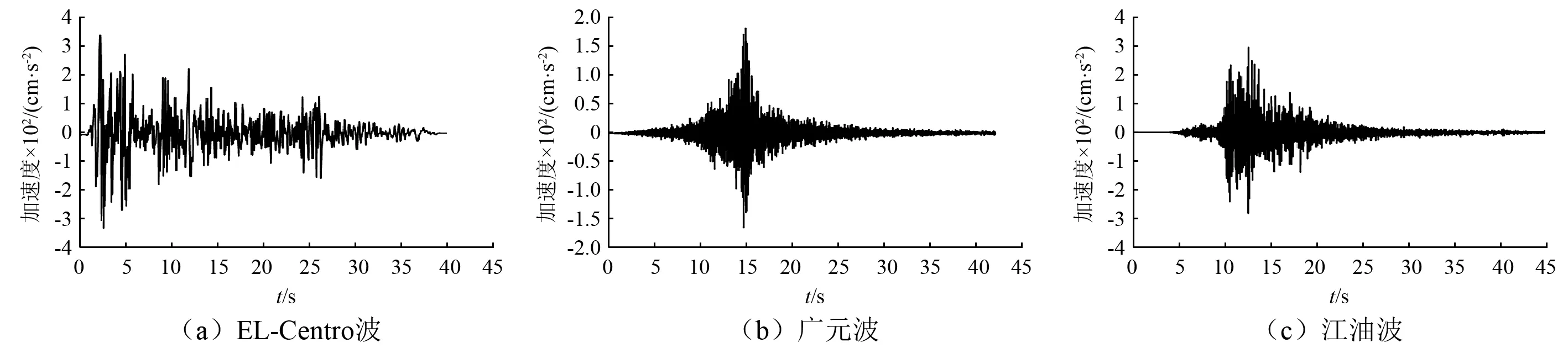
图6 输入地震动曲线Fig.6 Acceleration time history curve of input motions

2.4 试验结果

2.4.1 结构损伤分析

在7度和8度多遇地震作用下，结构的地震响应不明显，试验模型的晃动很难观察到；当振动台模型加载到9度多遇地震动时，观测到试验模型轻微的振动，且二层和顶层角柱的柱底均产生了细小的水平裂缝，中柱裂缝现象不明显，二层横向边跨梁产生了细小的竖向裂缝，其他框架梁震损现象不明显；7度罕遇地震动作用下，模型的晃动幅度增大，框架梁柱的裂缝长度和宽度有所增大；8度罕遇地震动工况下，前述工况阶段产生的裂缝均有所发展，并产生大量新的裂缝。结构二层及顶层角柱均产生明显的裂缝，但顶层比二层裂缝发展现象更为明显，顶层边柱柱底和部分中柱柱底分别产生了少量的贯通的水平裂缝，部分横向边跨梁也出现少量贯通的竖向裂缝；9度罕遇地震动工况下，结构晃动幅度增大，顶层振动相对更加剧烈，并且伴随着响声。前面工况产生的裂缝形成贯通裂缝，顶层的角柱柱顶内侧出现了混凝土的剥落，露出了钢筋，部分纵向边梁出现了贯通的斜裂缝。

由振动台试验过程分析得出，考虑结构和设备相互作用的振动台试验中电气设备所在层的框架柱在梁柱节点处首先发生了破坏，其产生的裂缝多于与其相交的梁端产生的裂缝，这是由于设备所在层的框架梁刚度较大，而设计的框架柱的刚度相对较小。同时电气设备在整个加载过程中未出现明显的破坏。

2.4.2 加速度分析

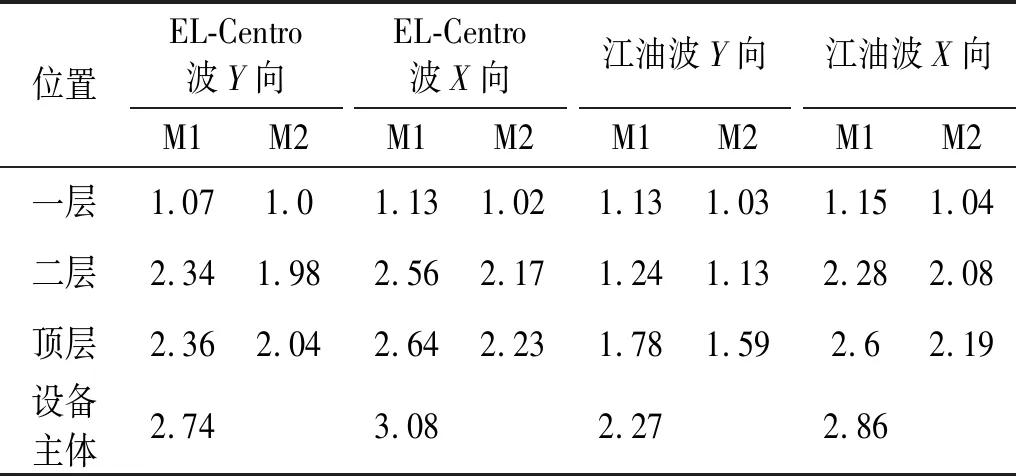
鉴于篇幅有限，本文在分析模型加速度变化情况时以8度地震作用为例，7度和9度地震作用规律类似，因此不再赘述。模型结构在8度地震作用下的加速度放大系数值见表3和表4。罕遇地震作用下三层底板中点位置加速度时程曲线见图7。其中，加速度放大系数为模型各层和设备主体与振动台台面加速度的比值。

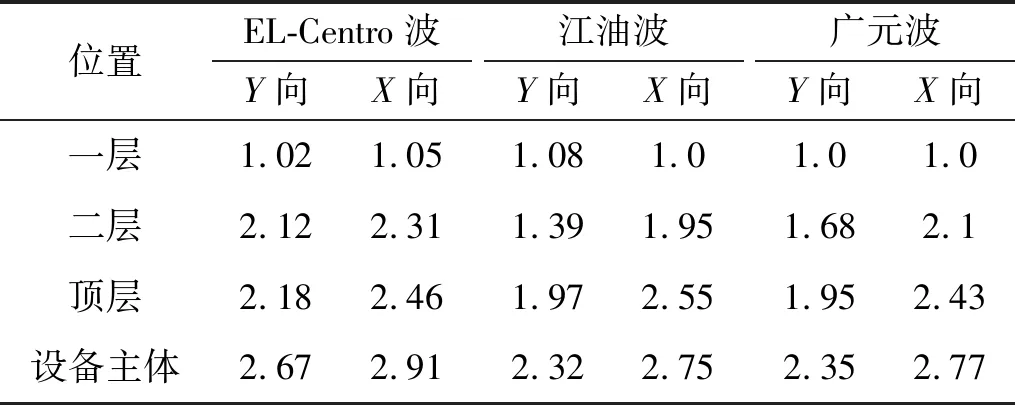
表3 多遇地震作用下结构加速度放大系数值

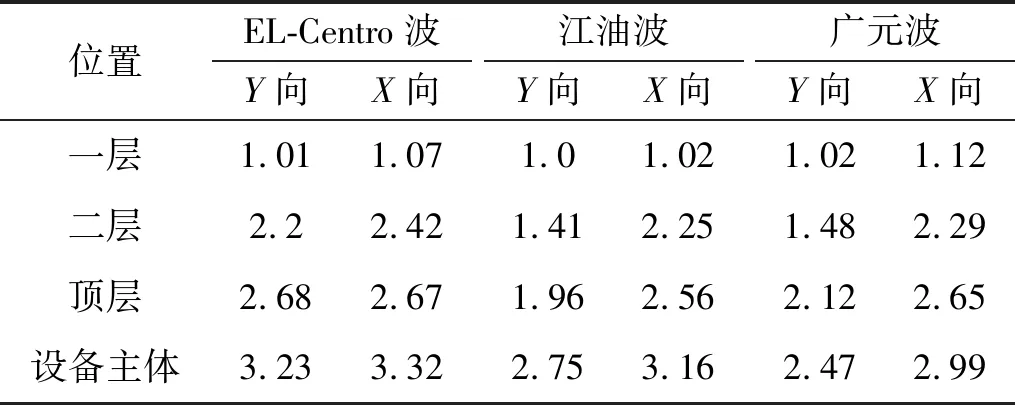
表4 罕遇地震作用下结构加速度放大系数值

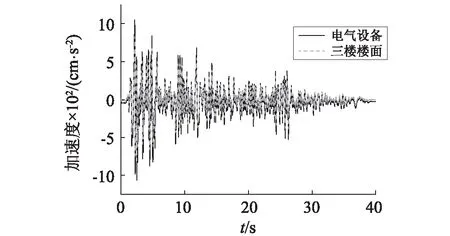
图7 EL-Centro波Y向罕遇地震时三层楼板加速度时程曲线Fig.7 Acceleration time history curve under EL-Centro

由表3～表4可知，结构各层加速度放大系数随楼层高度的增加而增大，且设备主体的加速度放大系数大于所在楼层的加速度系数。电气设备主体动力放大系数最大值为3.32(EL-Centro波X向)，大于《电力设施抗震设计规范》[14]规定—电气设备放置在楼层时动力放大系数取为2.0。

由图7可知，8度罕遇地震作用下，电气设备的加速度放大系数值均大于所在楼层的加速度放大值，比值在1.2～1.4，地震反应较所在楼层的地震反应强烈，说明在罕遇地震作用下变电站主体结构和电气设备的加速度运动不同步，且电气设备的动力放大效应明显。

2.4.3 位移分析

表5和表6给出了结构在8度地震作用下楼层相对位移的试验结果。其中楼层相对位移为绝对位移值相对于底座的位移。

表5 多遇地震作用下结构位移值

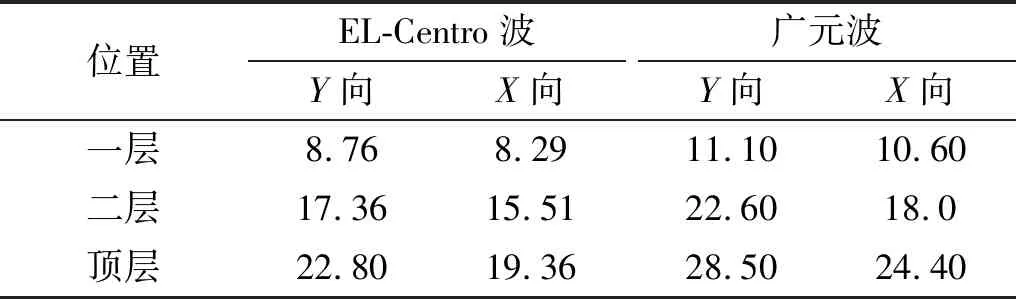
Tab.5 Displacement value under the action of earthquake mm

表6 罕遇地震作用下结构位移值

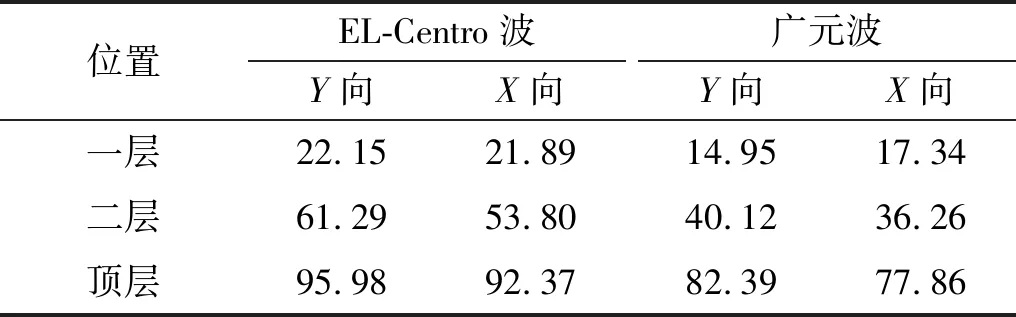
Tab.6 Displacement under the action of severe earthquake mm

由表5和表6可知，8度地震作用下，楼层的最大水平位移值随着楼层层高的增大而增大；结构顶层位移值比其他层数值大，且结构的层间位移角大于《建筑抗震设计规范》[15]1/50的要求。结构的顶层为楼层的薄弱层，结构设计时应加强构造措施。水平Y向位移值大于水平X向位移值，说明变电站主厂房结构水平Y向抗侧移刚度小于水平X向抗侧移刚度，该主厂房结构的抗震设计由水平Y向地震作用控制。

3 有限元模拟分析

3.1 有限元模型的建立

参照户内式变电站原型结构，在ABAQUS软件中通过编写命令流和实体界面操作建立考虑主-子结构动力相互作用的变电站模型。结构的混凝土本构采用损伤塑性模型；钢筋的本构模型是考虑包辛格效应的双线性动力强化模型。混凝土采用C3D8单元模拟，钢筋采用T3D2单元模拟，电气设备套管采用线性梁单元模拟，互感器、断路器、开关和开关柜采用线性壳单元模拟。实际结构中设备底部与结构楼板通过内嵌于楼板的槽钢条用螺栓连接固定，在数值模拟时设置绑定约束模拟设备和结构的连接。建立了考虑结构-设备相互作用且电气设备位于结构三层的变电站主厂房有限元模型M1和不考虑结构-设备相互作用的变电站主厂房有限元模型M2(即设备按等效均布荷载计算)，三维有限元模型如图8所示。其中，振动台试验模型为有限元模型M1的缩尺模型。模型采用tie约束方式耦合作用施加荷载；分析方法设置中使用完全Newton迭代法的动力时程分析，并定义时长和步数。

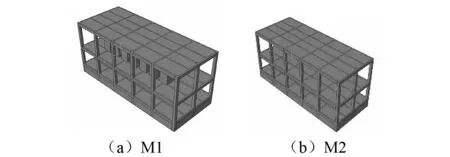
图8 结构模型图Fig.8 Model diagram of the structure

3.2 模态分析

结构的模态形式反映出结构的基本动力特性，为工程设计提供必要保障。对地震前后的白噪声扫描，得到了结构的动力特性。根据频率相似比将模型结构频率转化为原结构频率值，数值模拟和振动台试验的前五阶振型所对应频率对比值见表7。

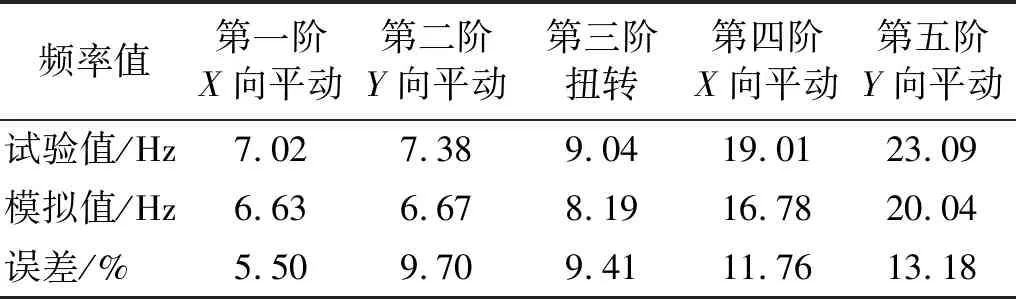
表7 频率对比值

由表7可得，地震作用下试验结果和有限元模拟结果的数值较接近，相对误差较小，最大误差在15%以内。误差来源于试验结果的偶然因素影响和两种模型实现结构和设备连接方式的差异。因此，不同地震作用下试验模拟和有限元模拟结果误差较小，从而证明数值模拟模型的正确性。

3.3 结构损伤分析

在7度和8度多遇地震作用下，模型M1中结构仅在二层和顶层的梁柱节点处出现了较小的受压和受拉损伤值。8度多遇地震作用下结构模型的整体损伤值如图9所示。9度罕遇地震动作用下，有限元模型中框架梁柱的受拉、受压损伤值均较大，结构构件震损模型见图10。

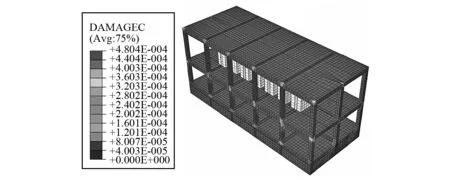
图9 8度罕遇地震作用下结构整体损伤图Fig.9 The damage of structure under 8 degree rare earthquake wave

图10 9度罕遇地震作用下构件损伤图Fig.10 The damage of elements under 9 degree earthquake wave

3.4 加速度分析

对比M1和M2在8度地震作用下水平加速度值，定量评估考虑主-子结构动力相互作用时设备对主厂房结构的动力放大效应。本文对模型M1和M2得到的结构各层加速度和设备加速度数值结果进行对比，结构在8度地震作用下的加速度放大系数值见表8和表9，设备所在楼层底板中点位置8度罕遇地震作用下加速度时程曲线如图11所示。

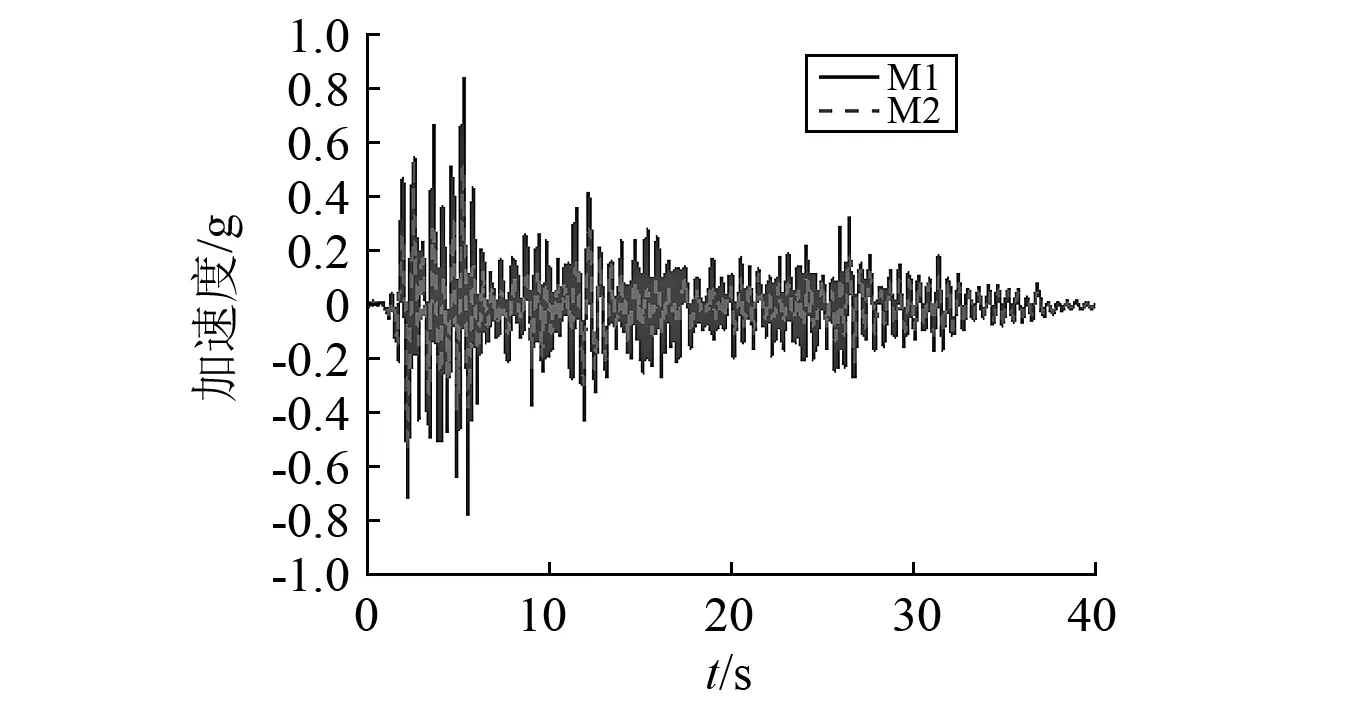
图11 EL-Centro波Y向地震三层底板加速度时程曲线Fig.11 Acceleration time history curve under EL-Centro

位置EL-Centro波Y向M1M2EL-Centro波X向M1M2江油波Y向M1M2江油波X向M1M2一层1.071.01.131.021.131.031.151.04二层2.341.982.562.171.241.132.282.08顶层2.362.042.642.231.781.592.62.19设备主体2.743.082.272.86

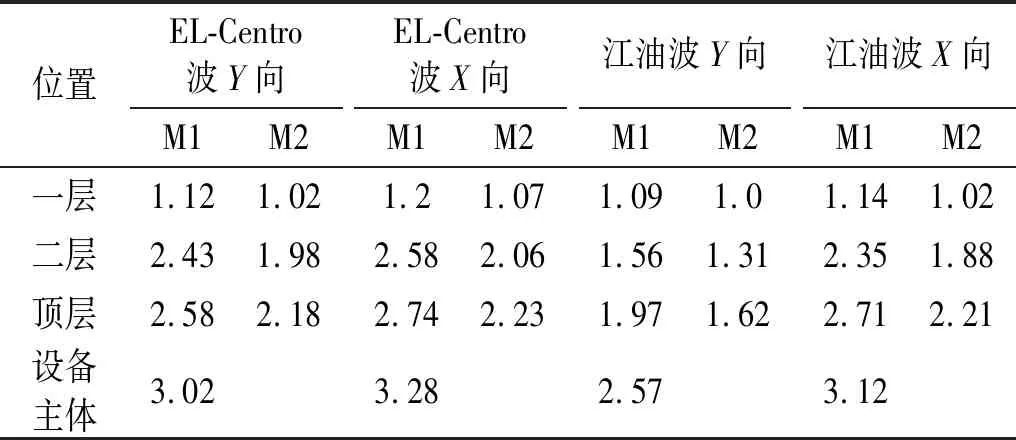
表9 罕遇地震作用下模型加速度放大系数值

由图11可知，8度罕遇地震作用下，模型M1中设备所在楼层的峰值加速度为0.89g，模型M2对应的峰值加速度为0.70g，考虑电气设备的存在时，主厂房体系楼层峰值加速度增大了1.27倍。对比M1和振动台试验模型得出的地震作用下结构加速度放大系数值(见表3和表4)，两者相对误差较小。由表8和表9得出，电气设备(中部位置)的加速度放大系数值均大于所在楼层的对应值，比值在1.2～1.4，地震反应较所在楼层的地震反应强烈。对比M1和M2在8度地震作用下水平加速度值，考虑设备的存在时，主厂房楼层的加速度放大系数值均增大。多遇地震作用下考虑设备作用的结构加速度放大系数值是不考虑主-子结构动力相互作用数值的1.15倍；罕遇地震作用下，其比值为1.25。因此，在地震作用下电气设备的动力放大效应明显，且考虑设备作用的结构加速度放大系数值增大。

3.5 内力分析

对比分析M1，M2在地震作用下的内力值，定量评估考虑主-子结构动力相互作用时设备对结构的内力影响值。以8度基本地震作用下，EL-Centro波X、Y向计算所得各层柱底剪力值为例(其他内力规律类似，不再赘述)，结果如表10所示。

由表10可知，8度罕遇地震作用下，模型M1的柱底剪力值均大于M2的柱底剪力，比值约为1.2倍，且电气设备所在的轴线2～轴线5区间的柱剪力比值较其他位置数值大。因此在大震作用下设备和结构相互作用明显，在抗震设计计算剪力时，应采用非相互作用模型的1.2倍；即对此类变电站进行剪力计算时，依据抗震设计规范中剪力计算值的1.2倍取用。

3.6 位移分析

对比M1和M2在8度罕遇地震作用下层间位移值，定量评估考虑主-子结构动力相互作用时设备对主厂房结构的位移影响值。本文对模型M1和M2得到的结构各层位移值结果进行对比，结构在8度地震作用下的层间位移值见表11和表12，设备所在楼层中点位置8度罕遇地震作用下位移时程曲线，如图12所示。

表10 结构模型柱底剪力值

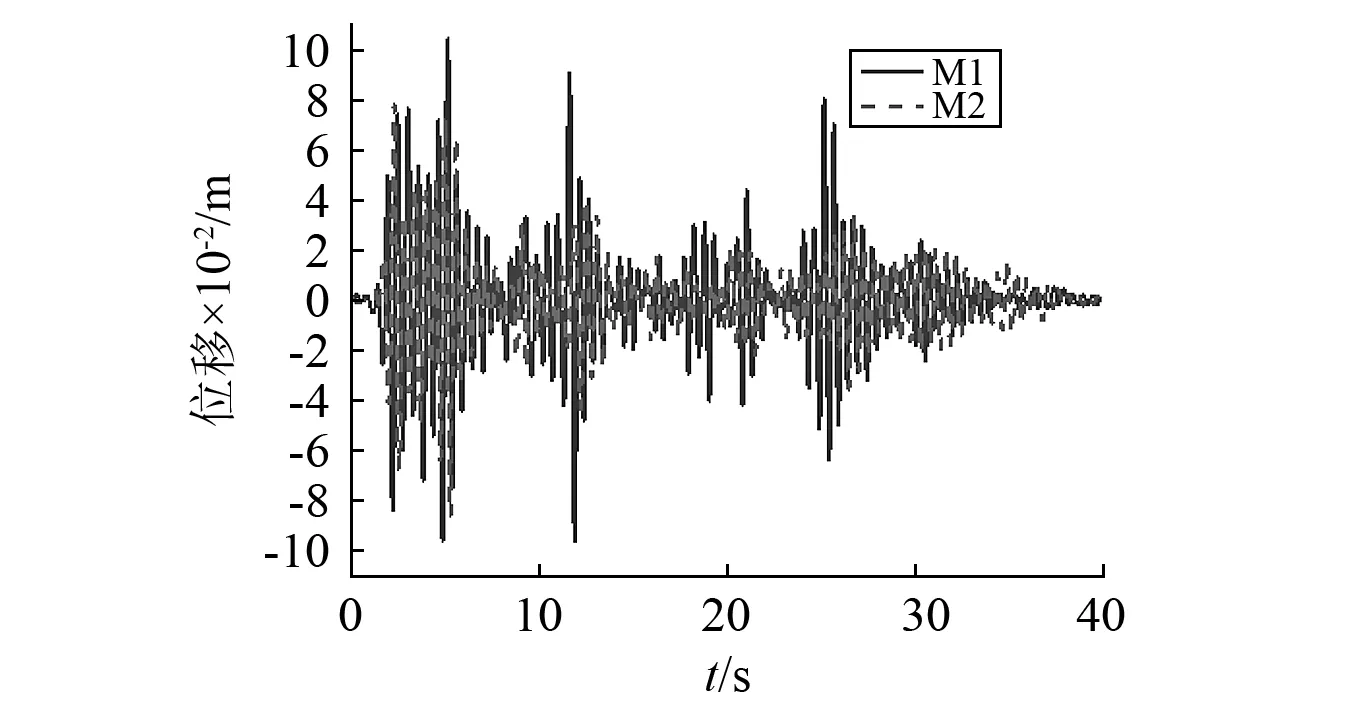
图12 EL-Centro波Y向地震三层底板位移时程曲线Fig.12 Displacement time history curve under EL-Centro

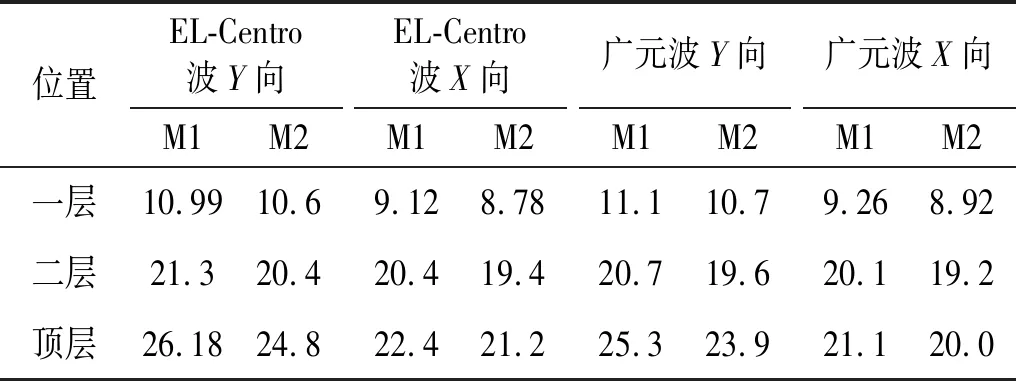
Tab.11 Displacement value under the action of earthquakemm

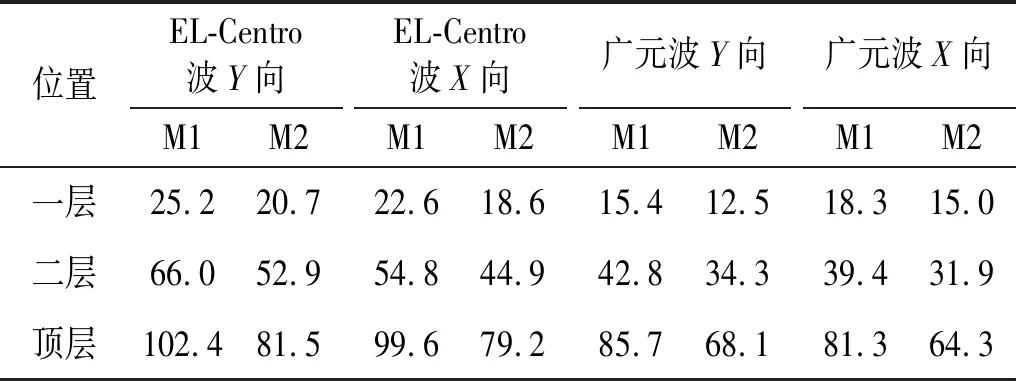
表12 罕遇地震作用下结构层间位移值

由图12可知，8度罕遇地震作用下，模型M1中设备所在楼层的位移值均大于模型M2所在楼层的对应值。由表11～表12得出，对比M1和M2在8度地震作用下层间位移值，考虑设备的存在时，主厂房楼层的位移值均增大。多遇地震作用下考虑设备作用的结构层间位移值是不考虑主-子结构动力相互作用数值的1.05倍；罕遇地震作用下，其比值为1.25。

在地震作用下，楼层的最大水平位移值随着楼层层高的增大而增大，结构顶层位移值比其他层数值大，顶层为结构的薄弱层。设备所在层位移差值比其它层位移差值大，由于电气设备位于结构三层，在同样的地震烈度下电气设备对结构楼层产生较大的惯性力，从而导致结构楼层位移增大，其中三层是惯性力直接作用的楼层，故三层的层间位移值最大。