基于EVMD-LNMF的复合故障信号分离方法

2019-08-31王梦阳王华庆任帮月宋浏阳

振动与冲击 2019年16期

王梦阳，王华庆，董方，任帮月，宋浏阳

(北京化工大学机电工程学院，北京 100029)

在旋转机械中，由于零部件产生故障的位置与程度各有不同，经常导致多种故障特征相互耦合在一起，相比单一故障形式，复合故障发生时给机械设备带来的危害更严重，诊断难度也更大，所以，对复合故障进行诊断具有重大意义。

盲源分离方法能够在缺少一定的先验条件下，仅通过传感器获取到的观测信号，便可以分离出未知源信号，是解决复合故障信号分离的有效方法之一[1]。其中，独立分量分析(Independent Component Analysis, ICA)，稀疏分量分析(Sparse Component Analysis, SCA)，非负矩阵分解(Non-negative Matrix Factorization, NMF)由于具有强大的理论优势和广泛的应用前景，已成为盲源分离的主流方法。然而，各种方法也都存在自身的不足，如当传感器采集到的观测源信号数目小于故障源数目时，即欠定盲分离问题，ICA和NMF算法无法直接应用；SCA算法虽然可以解决欠定盲分离问题，但要求源信号必须充分稀疏，对于实际信号很难有效提取稀疏源[2]。为了解决欠定盲分离问题，传统的方法采用经验模态分解 (Empirical Mode Decomposition,EMD)，集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)，变分模态分解(Variational Mode Decomposition, VMD)等算法将源信号扩充为多个虚拟的通道，再根据相关信息选取合适的分量进行盲源分离。如陈晓朦[3]将EMD与NMF算法结合实现了语音信号的盲分离；Wang等[4]运用EEMD以及ICA算法成功分离了轴承与齿轮箱复合故障信号；Tang等[5]采用VMD并结合ICA算法实现了轴承复合信号的盲分离。同时，Mirzaei等[6]提出基于贝叶斯非负矩阵分解实现了混响音频的盲分离；Abdali等[7]利用正则化非负矩阵分解实现声音信号的分离；文献[8]通过频域聚类的非负矩阵分解算法实现了心肺信号的分离提取。但各种算法也存在一定的局限性，如EMD方法出现的模态混叠、边界效应[9]；EEMD方法复杂度较大，计算时间较长；VMD方法虽然能有效避免模态混叠问题，但对于实际信号，很难在缺少先验知识的情况下，自适应地设定VMD中的模态个数，从而导致信号分解不彻底或出现过分解的现象。

针对VMD算法中模态分量个数选取方法存在的不足，且NMF算法由于缺少相关约束，对故障源相互耦合，特征信息较微弱分解效果并不理想，提出了基于能量收敛因子为判断准则的能量变分模态分解(Energy Variational Mode Decomposition, EVMD)与局部非负矩阵分解(Local Non-negative Matrix Factorization, LNMF)相结合的复合故障信号分离方法。EVMD算法能够自适应确定VMD算法中模态分量个数；LNMF算法可以有效地突出分解后的局部特征信息，将两者结合并应用在轴承复合故障诊断中，可以准确表达源信号所包含的故障成分，增强耦合故障特征信息，分离提取出更为清晰的故障特征。

1 基本原理

1.1 变分模态分解原理

VMD的实质是基于Wiener滤波、Hilbert变换和混频的变分问题求解过程，通过搜寻约束变分模型最优解来实现信号自适应分解[10-11]。相应的步骤可概括如下：

步骤1对于每一个模态分量um(t)，通过Hilbert变换，计算得到相关的解析信号

(1)

步骤2对每个解析信号，加入指数项调整各自预估的中心频率ωm，把每个解析信号的频谱调制到相应的基带上

(2)

步骤3中心频率ωm的带宽由以上解调信号的H1高斯平滑度来估算，这样就可以得到一个受约束的变分问题

(3)

步骤4在此基础上，引入二次惩罚因子和拉格朗日乘子，使其转换成无约束变分问题。其表达式为

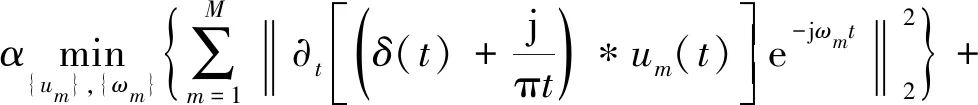
(4)

式中：α为惩罚因子；λ(t)为拉格朗日乘子。

这样变分问题就可以利用交替方向乘子算法来求解，通过交替更新中心频率和带宽，求取式(4)的鞍点，即得到多个模态分量，实现信号的自适应分解。

1.2 局部非负矩阵分解原理

NMF的基本思想可以简单描述为：对任意给定的一个非负矩阵A，NMF算法能够寻找到一个非负矩阵W和一个非负矩阵H，使其满足

An×m=Wn×rHr×m

(5)

从而将一个非负的矩阵分解为左右两个非负矩阵的乘积[12]。式中：n为矩阵的维数；m为样本个数；r为矩阵的秩。一般要求：nm>r(n+m)，即实现了数据的降维。LNMF方法是在传统非NMF基础上提出的，最初是应用在图像处理领域。LNMF算法是基于KL散度模型，对目标函数施加基的正交性约束，从而减少基向量之间的冗余。

LNMF算法的目标函数如式(6)所示

(6)

式中： [uij]=U=WTW； [aij]=A=HHT；α,β为正常数。

LNMF算法主要对目标函数施加三个约束条件[13]：

(3) 计算maxaii，使基向量有最大的代表性。

Wij与Hji的迭代公式为

(7)

(8)

(9)

2 基于EVMD-LNMF的复合故障分离方法

2.1 基于能量收敛因子VMD算法(EVMD)

根据VMD算法原理可知，利用该方法进行信号处理时，必须预先设定分解模态分量个数。然而，由于实际信号受现场复杂环境的影响，模态分量个数通常很难设定，这对算法的自适应性产生严重影响。现有大部分都采取观察中心频率的方法来确定模态分量个数，当相邻模态的中心频率过于相近时，即出现了过分解。但这种过于相近的情况并没有量化，均是根据经验判断。

针对模态分量个数选取方法存在的不足，提出了基于能量收敛因子为判据的EVMD，构造了能量收敛因子，并以其为判断准则来确定算法中模态分量个数，即原始信号经VMD算法分解后，计算分解之后模态的总能量，将所得能量的余量与原始信号的能量作比值，并定义相邻比值的差值为能量收敛因子Δ，如式(10)

(10)

式中：S为原始信号。

当Δ值小于一定阈值时，则认为能量收敛，此时信号分解相对完全。具体实现步骤如下：

步骤1初始化模态分量个数值M=2；

步骤2利用VMD算法对原始信号进行分解，得到多个模态分量um；

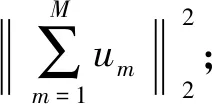
步骤4由式(10)，得能量收敛因子Δ，并更新模态分量个数M=M+1；

步骤5重复步骤步骤2～步骤4，直至满足迭代终止条件：能量收敛因子Δ<ε，结束循环，即可自适应得到最佳模态分量个数。根据经验及多组实验信号验证，文中取ε=0.02。(参考刘尚坤等的研究)

2.2 LNMF最优分解维数的获取

对于LNMF来说，数据降维后的维数是算法中的重要参数，直接影响到特征提取的效果。如果维数值选择过大，则会损失部分信息量，达不到准确降维的效果；维数值选择过小，则会降低分解精度，增大信息的冗余。本文采用邻近特征值占优法来确定维数值，即通过EVMD算法处理后，得到多个模态分量，加入原始信号组成多维信号模态矩阵Xm(t)，如式(11)

Xm(t)=[s,x1,x2,…,xm-1,xm]

(11)

然后，计算其协方差矩阵Rm(t)，并对协方差矩阵进行奇异值分解如式(12)

(12)

再对所有特征值采用降序排列，求取相邻特征值的比值，如式(13)

Λi,j={λi/λj},i=1,2,…,n-1;
j=i+1

(13)

特征值占优法根据相邻特征值之间的最大下降比速，即找出式(13)中的最大值，通过确定最大值来获取最优分解维数。

2.3 基于EVMD-LNMF的复合故障分离方法

针对轴承的复合故障，本文提出了基于EVMD-LNMF的故障分离方法，具体实现步骤如下，流程图如图1所示。

步骤1利用EVMD算法将信号自适应地分解为多个模态分量；

步骤2对多个模态分量采用邻近特征值占优法确定最优分解维数；

步骤3将分解后的多个模态分量重构，使其满足LNMF算法的输入矩阵A；

步骤4利用LNMF算法对矩阵A进行最优维数分解，得到基矩阵W和系数矩阵H；

步骤5对每个基矩阵W进行包络频谱分析，提取轴承的故障特征。

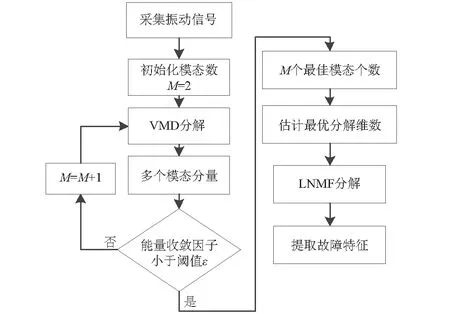
图1 轴承复合故障分离流程图Fig.1 Flow chart of bearing compound fault separation

3 仿真信号分析

为验证所提算法的有效性，使用两个不同的源信号通过随机矩阵混合为单通道的观测信号，具体表达式如式(14)和式(15)所示

(14)

S(t)=A[s1(t),s2(t)]T

(15)

式中：a1=0.4；f1=200 Hz；a2=1；fn=3 000 Hz为固有频率；g=0.1为阻尼系数；T=1/95 s为重复周期，即特征频率为95 Hz，采样频率fs=25 600 Hz，并取0.4 s时间片段，A=[0.814 7，0.905 8]，为一个随机产生的混合矩阵，通过式(15)混合得到复合信号S(t)，混合信号归一化后的时域波形图和频谱图，如图2所示。

根据所提出的方法，首先利用EVMD算法对原始信号进行处理，即根据“2.1”节中的步骤计算出不同模态数下能量余量的比值Ei(i=2,3,…)，结果见表1。进而得到能量收敛因子Δ12=0.928 1，Δ23=0.013 2。因为Δ23=0.013 2<ε，所以最佳分解模态个数为2。同时，因为模态个数为2，也可直接确定最优分解维数值为2。

表1 不同模态数下所得能量余量的比值

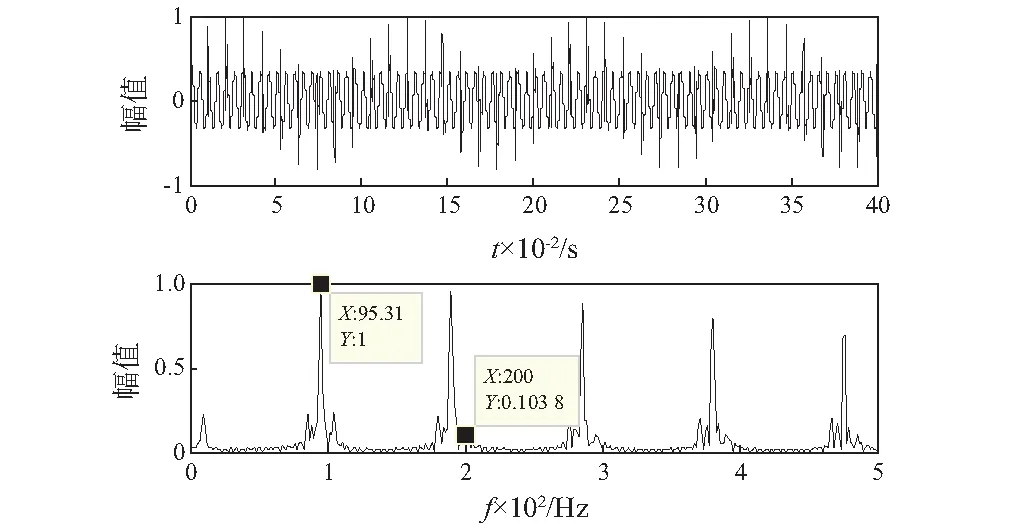
图2 仿真信号时域图及频谱图Fig.2 Waveform and spectrum of simulated signals

然后，对模态分量重构并作其局部非负矩阵分解，得到分离结果的时域图和频谱图，归一化处理后如图3和图4所示。

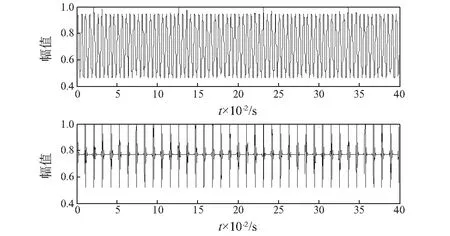
图3 分离信号时域图Fig.3 Waveform of separated signals

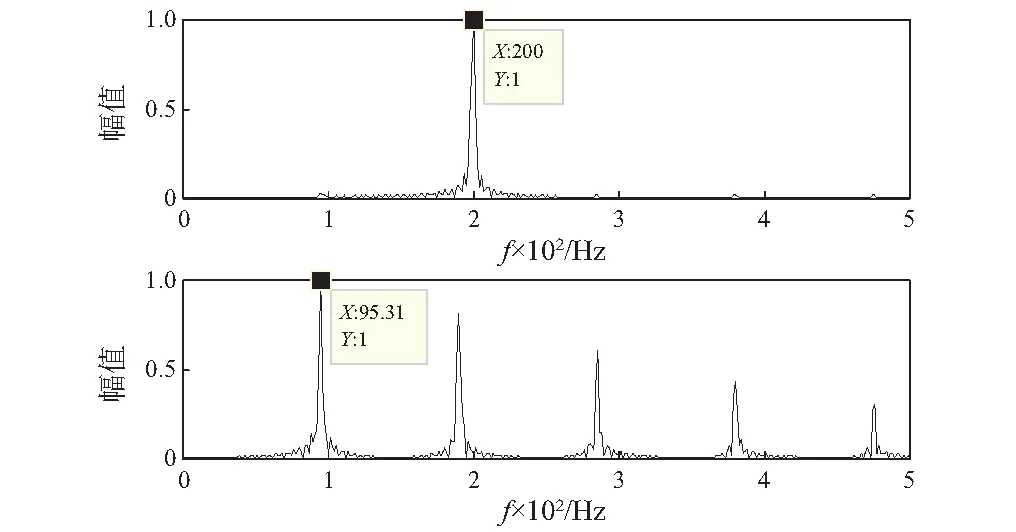
图4 分离信号频谱图Fig.4 Spectrum of separated signals

从图4可以看出，经EVMD-LNMF方法处理后可以分离得到两种信号成分，分别为200 Hz信号和95 Hz信号，这与所假定源信号特征成分相同。因此从仿真信号的分析中可以得出结论，本文所提出的方法可以有效地从混合信号中分离得到源信号，在频谱中也可以提取源信号特征频率，验证了该方法在复合信号分离的有效性。

4 实验验证

4.1 信号采集

为了进一步验证所提方法的有效性，采用实测的轴承信号为研究对象。采用NTN N204型号的圆柱滚子轴承，用线切割的方法分别在轴承的外圈和滚动体上加工宽度为0.5 mm、深度为0.15 mm的缺陷。将电机转速设为1 300 r/min和900 r/min，采样频率为100 kHz，采样时间为10 s。由式(16)和式(17)及轴承参数(见表2)可以计算得到滚动轴承各部件的理论特征频率，如表3所示。

表2 轴承NTN N204参数

表3 各部件的理论特征频率

外圈缺陷特征频率(fo)

(16)

滚子缺陷特征频率(fb)

(17)

式中：z为滚子数目；d为滚珠的直径；D为外节圆直径；α为滚子与保持架间的接触角；fr为电机转频。

4.2 结果分析

通过实验台采集得到1 300 r/min外圈与滚子复合故障信号，截取0.1 s数据片段归一化后的时域波形如图5所示。其归一化后的包络频谱图如图6所示。

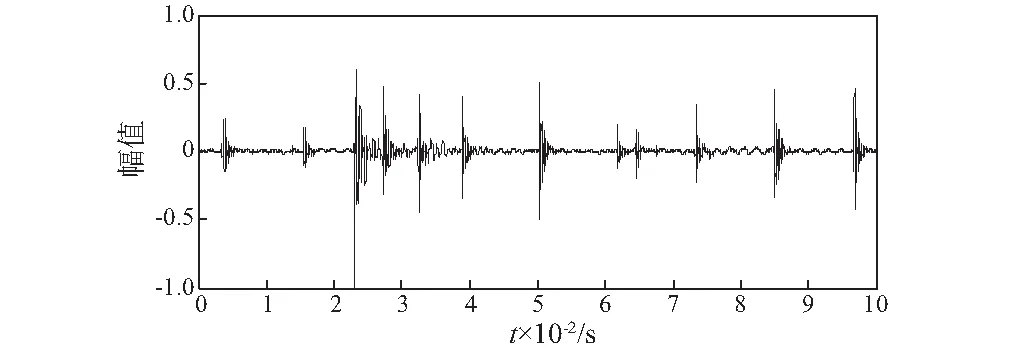
图5 原始信号时域图Fig.5 Waveform of signal

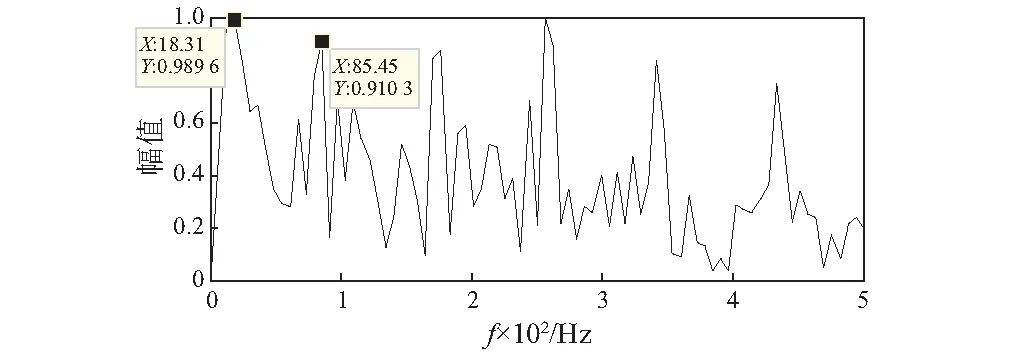
图6 原始信号包络频谱图Fig.6 Envelope spectrum of signal

由时域波形图可以明显地看出冲击性，表明该轴承已发生故障。在包络频谱图中，外圈缺陷特征可以明显识别出来，但是滚子缺陷特征被噪声成分淹没，难以识别。在频谱图中18 Hz左右处出现的峰值，该频率值与保持架的转动频率即轴承滚动体公转频率的二次谐波相近，因此该峰值可能是由滚动体运动冲击造成的。

根据论文提出的方法，首先利用EVMD算法对原始信号进行处理，即根据“2.1”节中的步骤计算出不同模态数下所得能量余量的比值Ei(i=2,3,…)，结果见表4，进而得到能量收敛因子Δij(i=1,2,…,M;j=i+1)，如表5所示。

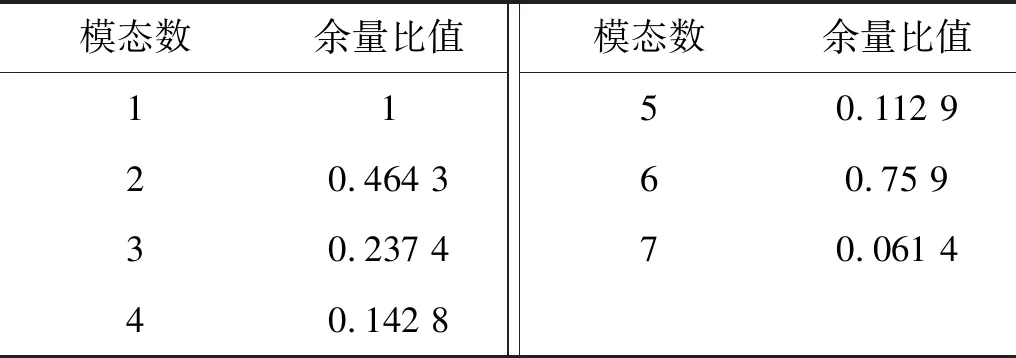
表4 不同模态数下所得能量余量的比值

表5 能量收敛因子

从表5可知，Δ67=0.014 5<ε，即可以认为信号分解完全，所以最佳分解模态数为6。

此时，将最佳的6个模态分量与原始信号组成模态矩阵，并对其进行协方差计算及奇异值分解，得到相应的特征值，如表6所示。

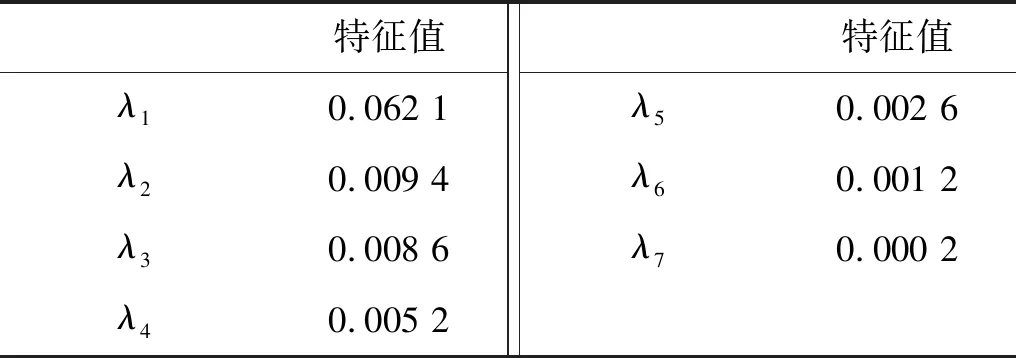
表6 模态矩阵特征值

根据表6，作相邻特征值的比值可得知， maxΛi,j=λ1/λ2=6.61，即LNMF中最优分解维数为2，也说明原始信号中存在两种故障源成分，通过LNMF分离并作归一化处理，得到的包络频谱图，如图7所示。

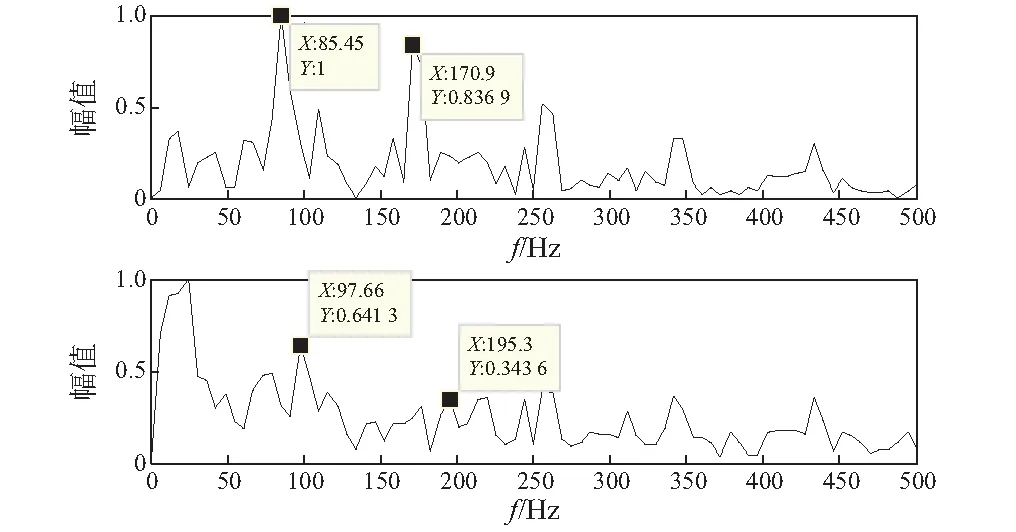
图7 EVMD-LNMF信号分离频谱图Fig.7 Spectrum of separated signals

由图7可知，经EVMD-LNMF方法处理后可以分离得到两种源信号成分，分别对应外圈故障特征频率和滚动体故障特征频率，这与理论计算出的特征成分相吻合，并且各自的高次谐波也被明显地提取出来。因此，从实验结果可以得出结论，本文所提出的方法可以有效地从单通道混合信号中分离出故障源信号，在包络频谱中也可以提取出故障特征频率，验证了该方法在轴承复合故障诊断中的有效性。

进一步验证所提方法的有效性，选用900 r/min外圈与滚子复合故障信号，截取0.1 s数据片段归一化后的时域图及包络频谱，如图8和图9所示。

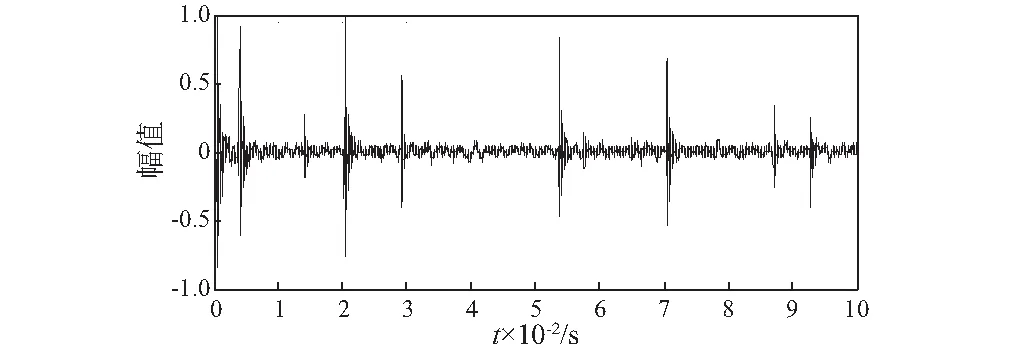
图8 原始信号时域图Fig.8 Waveform of signal

图9 原始信号包络频谱图Fig.9 Envelope spectrum of signal

通过所提出方法进行分离，并作分离后的包络频谱图，归一化后如图10所示。

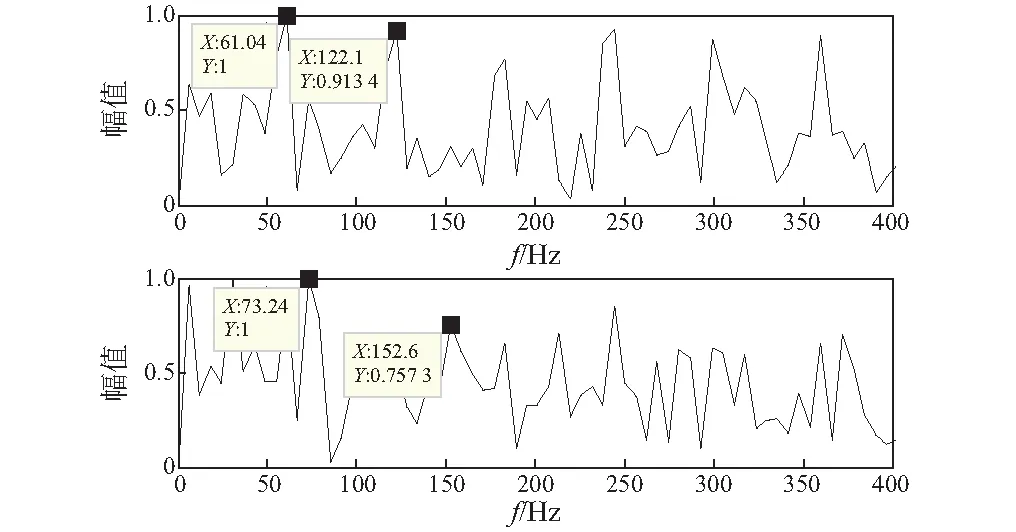
图10 EVMD-LNMF信号分离频谱图Fig.10 Spectrum of separated signals

从图10可知，经EVMD-LNMF方法处理后得到与理论值相吻合的外圈故障和滚动体故障特征频率，并且各自的高次谐波也被明显地提取出来。验证了该方法在轴承复合故障诊断中的有效性。

4.3 与VMD-LNMF算法对比分析

为了验证本文所提出基于能量收敛因子确定VMD算法中模态分量个数方法的优势，与未改进的VMD算法进行对比。这里选用1 300 r/min的实验数据，将未改进VMD算法中模态分量个数设为7，并对原始信号进行分解，得到7个模态分量，将模态分量重构使其满足LNMF算法的输入矩阵。然后对重构的模态矩阵采用LNMF算法分离，得到两个源信号，归一化后作其包络频谱图，如图11所示。

图11 VMD-LNMF信号分离频谱图Fig.11 Spectrum of separated signals

从图11可知，存在于原始信号中的两种故障源成分，经过未改进的VMD与LNMF算法处理后，并未得到有效分离，仅可以识别出外圈故障特征频率成分，而滚动体故障成分被淹没。说明当VMD算法中模态分量个数未达到最优值时，信号不能得到有效分离。

4.4 与EVMD-NMF算法对比分析

为了验证LNMF算法在轴承复合故障诊断的优势，分离阶段采用传统的NMF算法进行对比。首先将VMD算法中模态分量个数设定为最优值6，并对原始信号进行分解，得到6个模态分量，将其重构满足其作为NMF算法的输入矩阵，然后采用传统的NMF算法对重构的模态矩阵分离，得到两个源信号，归一化后作其包络频谱图如图12所示。

图12 EVMD-NMF信号分离频谱图Fig.12 Spectrum of separated signals

从图12可知，经过EVMD与传统NMF算法处理后，并未对原始复合故障信号实现有效分离，仅外圈故障特征频率成分比较明显，滚动体故障成分被淹没。而通过LNMF算法可以有效地分离出外圈和滚动体故障成分，对比图12和图7可知，由于LNMF增强了基向量之间的独立性，因而可以分离出源信号。图12中由于传统NMF算法缺少相关约束，导致基向量之间存在冗余，无法准确描述两个故障源信号。从而验证了LNMF在轴承复合故障诊断中的独特优势。