基于正负刚度并联永磁隔振器的隔振性能分析及实验验证

李 强， 徐登峰， 李 林， 魏绍炎

(1. 武昌理工学院 信息工程学院，武汉 430223； 2. 清华大学 机械工程系，北京 100084)

在超精密测量、IC(Intergraded Circuit)制造、光学、医学、高端物理和化学实验中，需要高性能的隔振器抑制外界干扰带来的影响[1-5]。尽管空气隔振器具有良好的隔振性能，但使用条件受限，需要研发满足新需求的隔振器。近年来，随着稀土永磁材料的迅速发展，钕铁硼永磁材料具有较强的剩磁、矫顽力和磁能积，许多学者利用永磁材料的这些特性进行永磁隔振器的研究，成为隔振器研究的新方法[6-8]。从现有的文献可查永磁隔振器的固有频率大约在5～8 Hz，隔振性能略差于现有的被动双腔室空气隔振器。然而，为了提高隔振器的隔振性能，在隔振器的研究中，诸多学者基于Platus的负刚度原理，采用正负刚度并联方式是提高被动隔振器隔振性能有效的方法[9-14]。因此，本文基于Platus负刚度原理，提出一种正负刚度并联永磁隔振器的新构型，永磁弹簧提供正刚度，橡胶带提供负刚度，负刚度部分地抵消正刚度，降低永磁弹簧的刚度，提高该永磁弹簧的隔振性能。为了进一步研究该永磁隔振器的隔振性能，建立了橡胶带拉力和刚度的解析模型，通过动力学方程对其隔振性能计算和分析，搭建了永磁弹簧和正负刚度并联隔振器的实验台，分别将实验结果与理论计算进行对比分析，获得该正负刚度永磁隔振器的隔振性能及特点。

1 正负刚度并联永磁隔振器的新构型及工作原理

采用一对环形永磁体与橡胶带组合，提出一种新构型的隔振器，每个单元的内环形永磁体轴向磁化，外环形永磁体径向磁化(内外环形永磁体等高，磁化方向用粗箭头表示)，轴上呈现斥力，可支撑负载。在该隔振单元中，上下各三根橡胶带，橡胶带的两端分别与永磁弹簧的内外磁环固接，如图1所示。由该四个隔振单元(见图1)组合使用，构成了一个正负刚度并联的永磁隔振器，如图2所示。

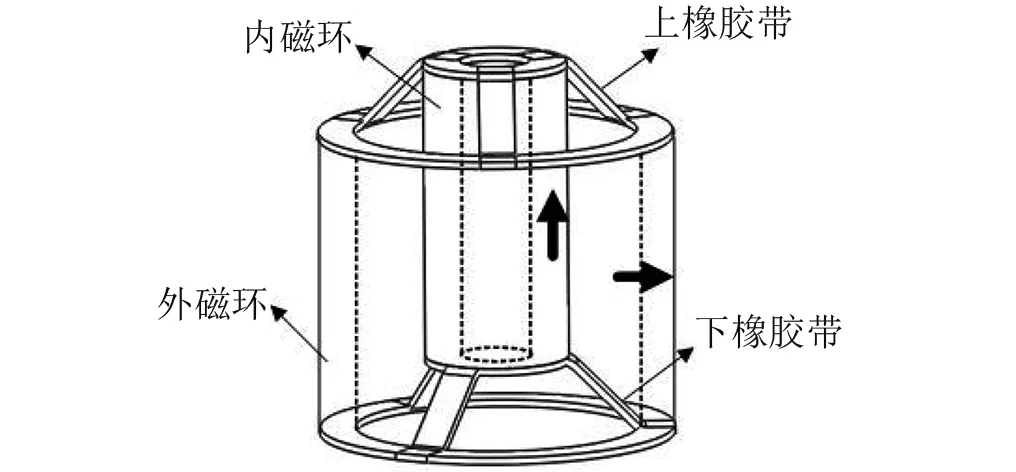
图1 正负刚度并联永磁隔振单元的结构Fig.1 The configuration of an MLVI unit

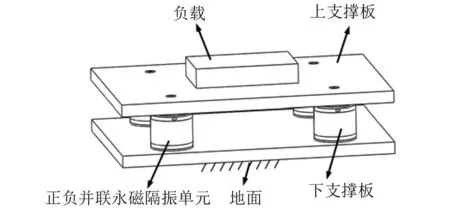
图2 正负刚度并联永磁隔振器Fig.2 The configuration of an MLVI

图3为永磁环与橡胶带的位置关系。图4为其工作原理图。二者的结构参数及相应的物理含义如表1所示。

图3 一个隔振单元橡胶带与永磁弹簧位置关系的四分之一剖面图(粗箭头代表磁环磁化方向)Fig.3 A quarter cross-section view of the relative position between the permanent magnet spring and the rubber ligaments of an MLVI unit (The arrow represents the magnetization of the permanent magnets)

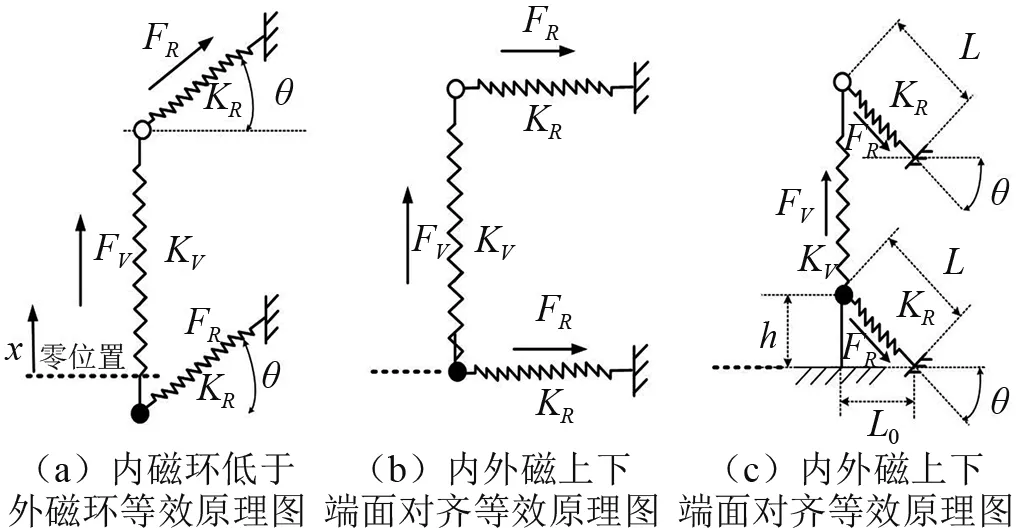
图4 一个隔振器单元橡胶带与永磁弹簧的工作原理图Fig.4 The schematic diagram of an MLVI uint

参数物理含义FR橡胶带拉力FV磁弹簧轴向磁力KR橡胶带刚度KV磁弹簧轴向刚度Ktotal一个正负刚度并联隔振单元轴向总刚度L0橡胶带初始长度θ橡胶带与水平位置夹角L橡胶带被拉伸后的长度

假设Ktotal为一个隔振单元的轴向(x方向)总刚度，KV为永磁弹簧轴向(x方向)刚度，KR为橡胶带的刚度。由图3(a)和图4(a)可知，当内磁环的位置低于外磁环时，该隔振单元的轴向总刚度Ktotal可表示为

Ktotal=KV+KRsinθ

(1)

当内外磁环的上下端面对齐时，由图3(b)和图4(b)可得该隔振单元轴向总刚度Ktotal可表示为

Ktotal=KV

(2)

当内磁环位置高于外磁环时，由图3(c)和图4(c)可得该隔振单元的轴向总刚度Ktotal可表示为

Ktotal=KV-KRsinθ

(3)

式(1)为当内磁环位置低于外磁环时，永磁弹簧与橡胶带的刚度方向相同，橡胶带有增强永磁弹簧的轴向刚度作用；式(2)为当内外磁环上下端面对齐时，橡胶带没有被拉伸，轴向刚度为零，橡胶对永磁弹簧的轴向刚度没有影响，隔振单元轴向刚度为永磁弹簧的刚度；式(3)为当内磁环的位置高于外磁环的高度时，橡胶带在永磁弹簧斥力的作用下被拉伸，橡胶带产生与永磁弹簧相反的刚度，能够部分抵消永磁弹簧的轴向刚度，构成了正负刚度并联的永磁隔振单元，降低了永磁弹簧的刚度，提高永磁弹簧的隔振性能。因此，以图1和图3(c)所示的结构及图4(c)的工作原理图展开该正负刚度并联永磁隔振器的隔振性能研究。

2 橡胶带垂直拉力和刚度的数学模型

2.1 橡胶材料Mooney-Rivlin模型本构关系

图5为一个正负刚度并联永磁隔振单元工作时橡胶带拉伸的局部剖面图，假设橡胶带的初始长度为Lo，橡胶带在磁力的作用下，被单向拉伸后的长度为L。假设橡胶是各项同性的，且不可压缩的(I3=0)，Mooney-Rivlin给出了橡胶应变能函数

图5 一个正负刚度并联永磁隔振单元工作时橡胶带拉伸的局部剖面图Fig.5 A part sectioned view of a stretched rubber ligaments of the MLVI unit

(4)

其中,

(5)

I2=(λ1λ2)2+(λ2λ3)2+(λ3λ1)2

(6)

(7)

λ1=1+εi

(8)

式中：I1,I2,I3称为变形张量不变量；λ1,λ2,λ3是三个方向的拉伸比。

由于橡胶材料的不可压缩性， 式(4)中的I3=0，橡胶材料应变能的函数为

(9)

式中：W(I1,I2)为应变能函数；Cij为Rivlin系数。对于橡胶在小范围的变形， 常用式(9)中关于I1和I2的线性应变能函数为[15-16]

W(I1,I2)=C10(I1-3)+C01(I2-3)

(10)

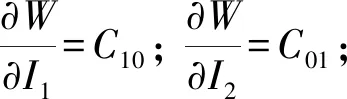
(11)

σ1=-p+2(C10λ2-C01λ-2)

(12)

σ2=σ3=-p+2(C10λ1-C01λ-1)=0

(13)

式中：p为静水压力，解出式(13)中的p，并代入式(12)可得橡胶在个拉伸比状态下及对应的应力为

σ1=2(λ2-λ-1)(C10+C01λ-1)

(14)

式中：C10和C01为橡胶材料系数；λ为受拉方向的拉伸比。

2.2 橡胶材料系数的确定

为了确定式(14)中的系数C10和C01，将式(14)变形可得

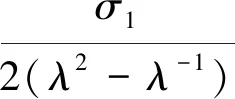
(15)

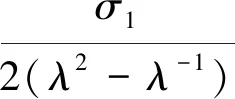
(16)

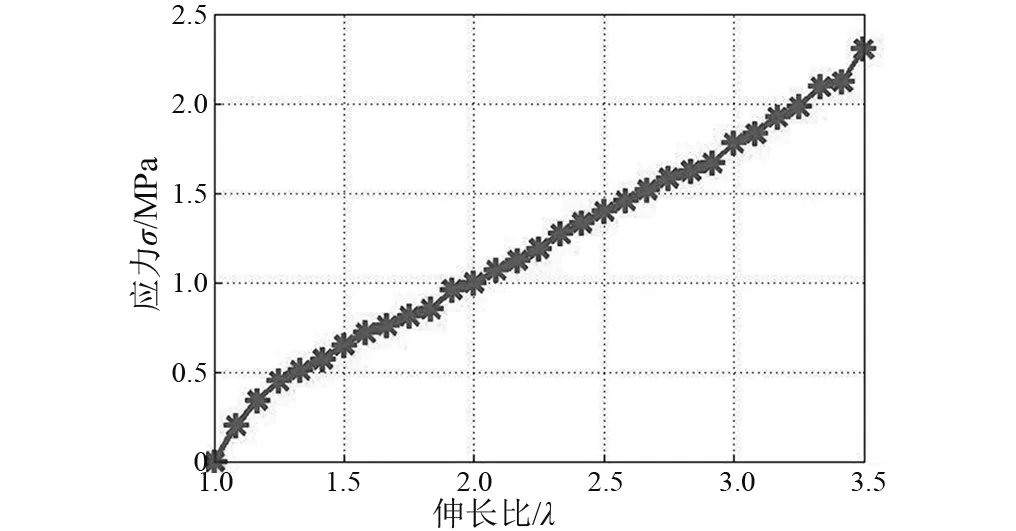
图6 橡胶带的应力-伸长比曲线Fig.6 The curve of the stress-stretched ratio of the rubber ligament

图7为式(16)的实验和拟合曲线，从图7可知，实验数据和拟合曲线较吻合。因此，可采用式(14)估算橡胶带在不同拉伸比时，橡胶带横截面上的应力，即

σ1=2(λ2-λ-1)(0.329 1λ-1-0.010 4)

(17)

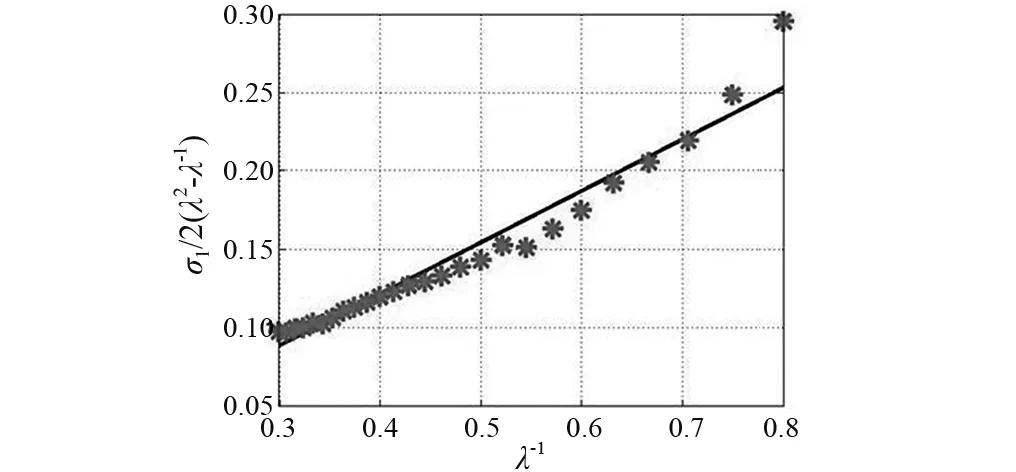
图与的实验与拟合曲线Fig.7 The fitted curve of the rubber ligament

2.3 橡胶带拉力和刚度的数学模型

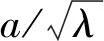
(18)

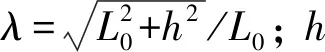
图8 橡胶带拉伸图Fig.8 The diagram of an arbitrary stretched rubber ligament

为了验证橡胶带拉力解析表达式的有效性，采用机床和传感器对一个隔振单元橡胶带的轴向拉力进行测试，测试装置设计如图10。该隔振器所用的单根橡胶带的尺寸为110 mm×7 mm×1.5 mm，一个隔振单元橡胶带拉力的测试如图11。当机床主轴轴向每移动0.25 mm，记录一次数据，进行5次实验，求得其平均值，实验曲线如图9所示。

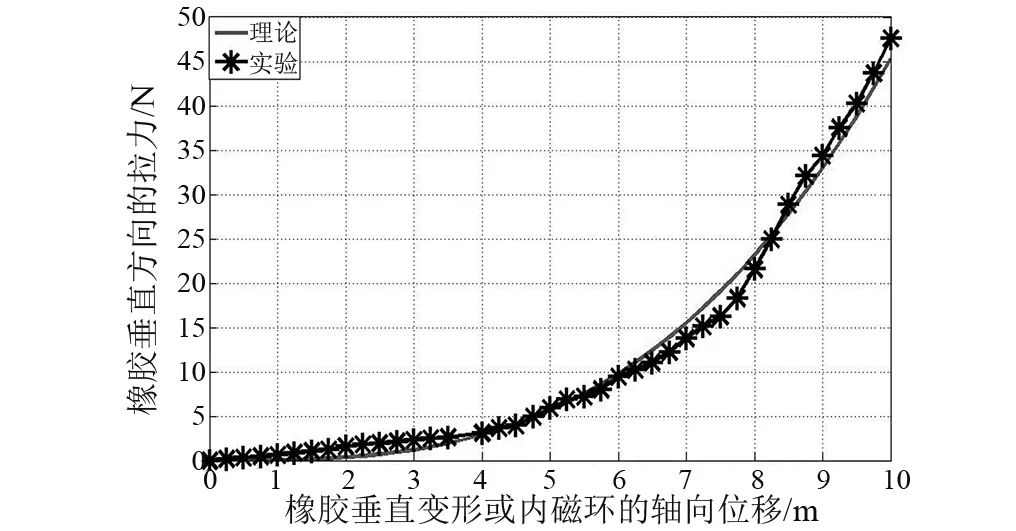
图9 一个隔振单元橡胶带轴向拉力计算与实验曲线Fig.9 The comparison curves of calculation and experiment of the stretched force for an MLVI unit in vertical direction

图10 橡胶带拉力测试原理图Fig.10 The schematic diagram of the experimental device of the vertical stretched force of an MLVI unit for the rubber ligament

图11 橡胶拉力测试图Fig.11 The test of the stretched force of an MLVI unit

从图9可知一个隔振单元橡胶带垂直方向拉力的计算值和实验值之间有一定的误差，误差主要由以下几个方面造成的：①Mooney-Rivlin公式中的常数C10和C01是通过橡胶拉应力实验数据拟合得到的，可能存在一定的误差；②一个正负刚度并联隔振器单元橡胶带拉力测试过程中，附加装置的几何主轴线和机床的主轴线没有绝对重合，在实验的过程中会产生一定的偏心，可能6根橡胶带拉伸长度不一致，也会产生一定的误差；③由于橡胶材料的不均匀性也可引起实验值和理论值的误差。因此，对于橡胶这种超弹性材料，可以用式(18)来估算该正负刚度并联隔振单元单根橡胶带的轴向拉力。

基于力与位移的关系，对式(18)轴向位移h微分可得单根橡胶带垂直方向刚度的解析表达式

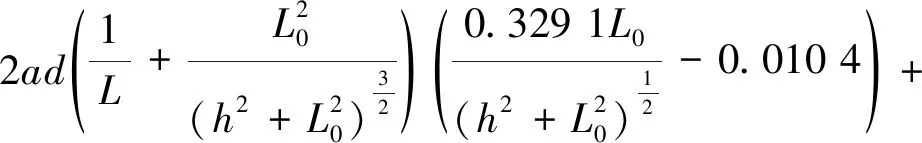
(19)

式(19)和式(18)中的参数具有相同的物理含义。图12为一个正负刚度并联永磁隔振单元橡胶带的轴向刚度曲线。从图12可知，橡胶垂直方向的刚度也是非线性的，橡胶带垂直方向的拉力和刚度有相同的变化趋势，均随着内磁环轴向位移增加而增大。

图12 一个正负刚度并联隔振单元橡胶带轴向刚度曲线Fig.12 The vertical stiffness of the rubber ligament of an MLVI

3 永磁弹簧轴向磁力和刚度的数学模型

对于环形永磁体的轴向磁力模型，Yonnet[17]给出了基本表达式，李强等进行了进一步研究，并给出了一对环形永磁体轴向磁力的解析表达式F(h)

(20)

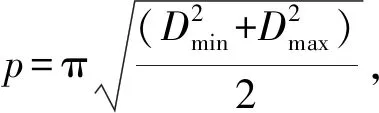
表2 永磁弹簧的结构参数

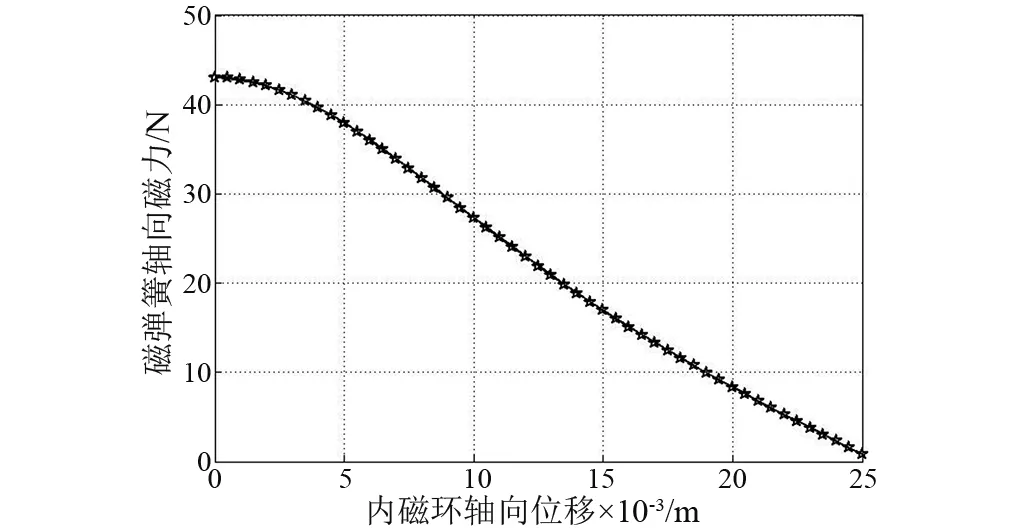
图13 永磁弹簧的轴向磁力Fig.13 The vertical magnetic force of a PMS

式(20)表明磁力F(h)是h的显示函数，以h为变量，对F(h)进行微分可得其轴向刚度的解析表达K(h)

(21)

式(21)和式(20)中的参数有相同的物理含义，结构和性能参数如表3，图13为一对环形永磁体的刚度曲线。从图13和图14可知，当内磁环的轴向位移趋近于零时，轴向磁力最大，刚度具有最小值，随着内磁环轴向位移的增加，轴向磁力减小，但刚度是增加的。因此，本文以该永磁弹簧为基体，选取该永磁弹簧的承载能力最大，轴向刚度较小区域(0～5 mm)为工作范围，研究其隔振性能。

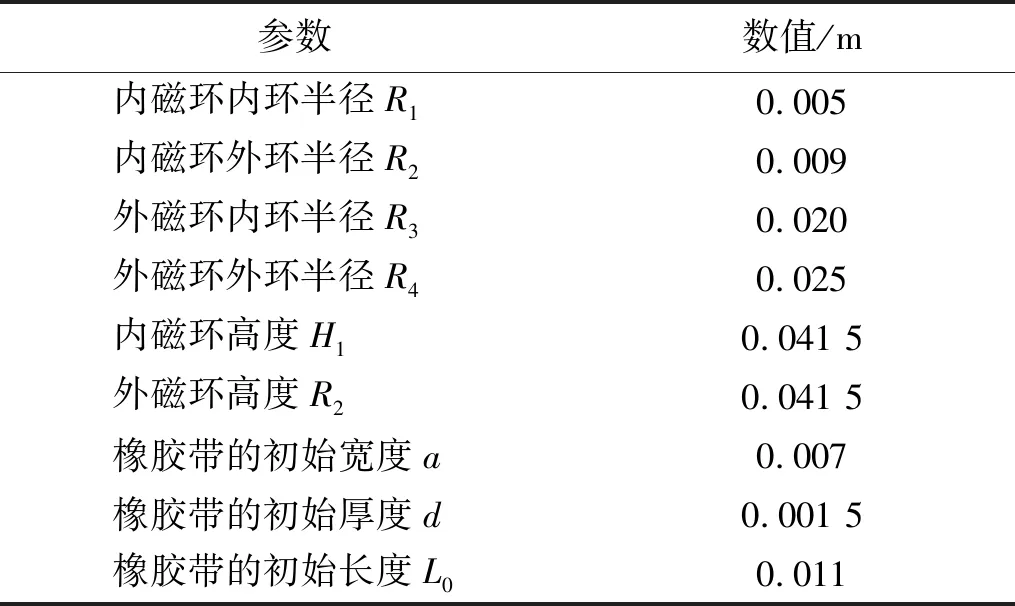
表3 永磁弹簧和橡胶带的结构参数

图14 永磁弹簧的轴向刚度Fig.14 The vertical stiffness of a PMS

4 永磁弹簧和正负刚度并联永磁隔振器的动力学计算与实验

4.1 动力学计算与分析

该隔振器由四个正负刚度并联永磁隔振单元和两块铝板组成，永磁弹簧的外磁环固定在下支撑板上，内磁环通过附属装置固定在上支撑板上，负载在磁斥力的作用下被悬浮，在橡胶带的作用下处于平衡位置。以地面的信号为输入信号，上支撑板及负载振动为输出信号，当地面的振动传递到隔振器上支撑板时，永磁弹簧和正负刚度并联永磁隔振器均可等效为一个单自由度的永磁弹簧阻尼系统，动力学方程可表示为

(22)

式中：M为隔振器的承载能力；C为隔振器的阻尼系数；K为隔振器的刚度；y为隔振器的输入信号(地面的振动)；x为隔振器输出信号。

对式(22)拉式变换可得隔振器传递率函数为

(23)

若要计算该隔振器的传递率，则需计算阻尼系数C，承载能力M和刚度K。然而，该隔振器是一个弱阻尼系统，阻尼项包括橡胶阻尼、永磁体的涡流以及上支撑板和负载与空气之间的摩擦，很难从理论上计算阻尼系数C，可采用半功率点来估算。

该隔振器承载能力可通过式(18)和式(20)计算

(24)

式中：m为一个正负刚度并联隔振单元的承载能力；F(h)为永磁弹簧的磁力；F(h)RV为橡胶垂直方向拉力的分力； 与磁力方向相反，承载能力与内磁环的轴向位移的关系，如图15所示。

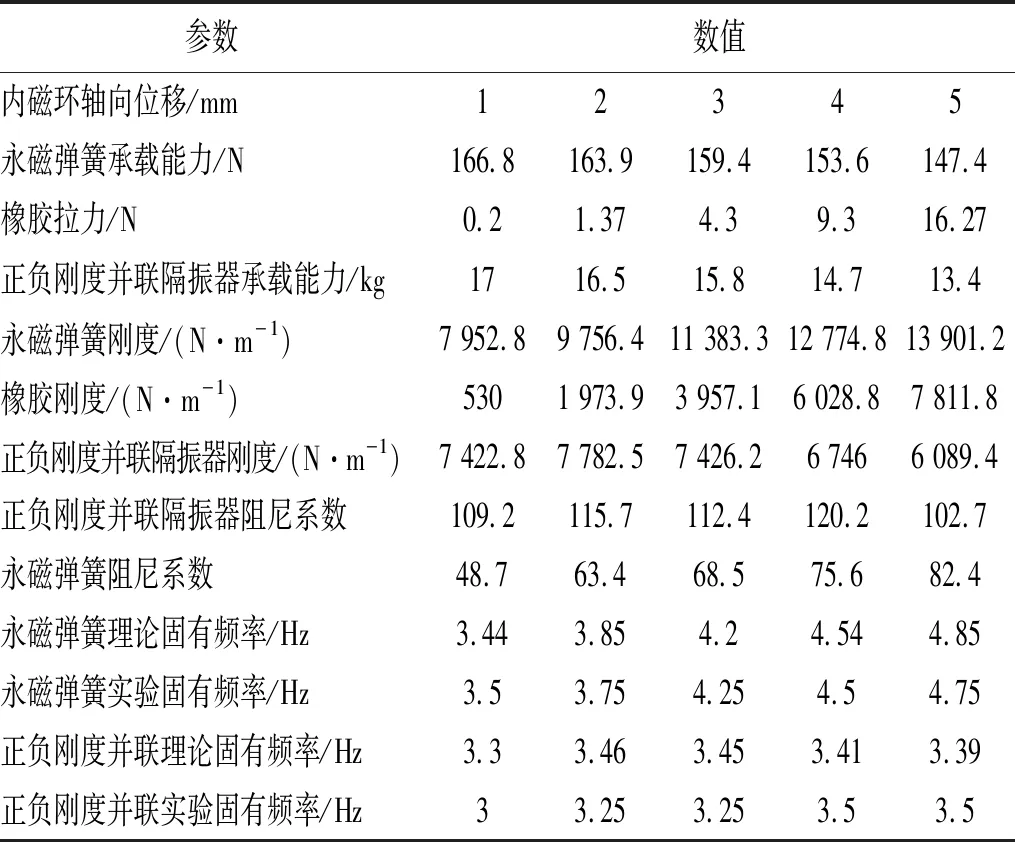
表4 永磁弹簧和正负刚度并联永磁隔振器的性能参数及实验数据

图15 一个正负刚度并联永磁隔振单元的承载能力Fig.15 The vertical load capacity of an MLVI unit

同理，可运用式(19)和式(21)可得一个正负刚度并联隔振单元的轴向刚度

K=K(h)-K(h)RV

(25)

式中：K为一个正负刚度并联隔振单元刚度；K(h)为永磁弹簧轴向刚度；K(h)RV为橡胶刚度的垂直分量，其刚度曲线如图16。从图15和图16可知，尽管橡胶部分抵消了永磁弹簧的轴向磁力和刚度，但在内磁环轴向位移为零时，该正负刚度并联永磁隔振器的承载能力最大，刚度最小。

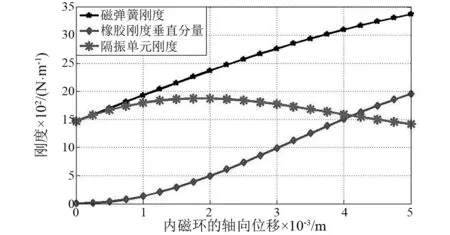
图16 一个正负刚度并联永磁隔振单元的刚度Fig.16 The vertical stiffness of an MLVI unit

4.2 实验验证

当地面的微幅振动被传递到隔振器的负载和上支撑板时，负载和上支撑板也作微幅振动。该隔振器的承载能力和刚度可以在其平衡位置进行线性化，作为一个研究事例，选取一对环形永磁体和橡胶带的结构参数，如表3所示。通过式(24)和式(25)进行计算，如表4所示。同理，可用式(20)和式(21)计算永磁弹簧的承载力和刚度。由于永磁弹簧和正负刚度并联的永磁隔振器均是弱阻尼系统，半功率点估算的阻尼系数，如表4所示。

为了验证正负刚度并联永磁隔振器的隔振性能，进行对比实验，根据“4.1”节理论计算的结构参数，分别搭建永磁弹簧和正负刚度并联永磁隔振器实验台，如图17所示。同时，为了克服永磁体的不稳定性，在永磁弹簧隔振实验中，在垂直方向采用空气轴承作为导向装置，将负载稳定在平衡位置，使其沿空气轴承轴向运动，如图17(a)所示。图17(b)为正负刚度并联永磁隔振器的实验装置，分别用HANDYSAM低频隔振仪进行隔振性能测试。

4.3 实验结果分析

从正负刚度并联永磁隔振器的理论计算和实验可以得到一下几点结论：首先，从图18可知该正负刚度并联永磁隔振器的理论计算传递率和实验测试的结果存在一定的误差。一方面是由于橡胶材料的超弹性，不能精确的将内磁环控制在精确的理论计算位置；另一方面橡胶拉力和刚度模型中的Mooney-Rivlin参数C10和C01是拟合得到的，橡胶材料的不均匀性均可引起误差的存在。其次，从图18和图19对比分析可得这种正负刚度并联的方法对该隔振器的研究是有效的。橡胶带提供与永磁弹簧方向相反的刚度，可部分抵消磁弹簧的刚度，降低了整个隔振器的刚度，提高了单一永磁弹簧的隔振性能。再次，采用该种永磁弹簧与橡胶带进行隔振器的研究，该隔振器的优点在于承载能力最大时，刚度最小，固有频率最低，对应的隔振性能最好。此外，采用该种方法进行永磁隔振器的研究，橡胶的拉力会影响永磁弹簧的承载能力，但削弱刚度，提高隔振性能是主要的，需要选择二者合适的结构尺寸，获得最佳隔振性能。而橡胶的历史变形，工作温度，使用时间、材料的差异和不均匀性均也可影响该隔振器的隔振性能，这将是下一步的研究。

图17 隔振器隔振性能测试实验Fig.17 The photograph of the vibration isolator table

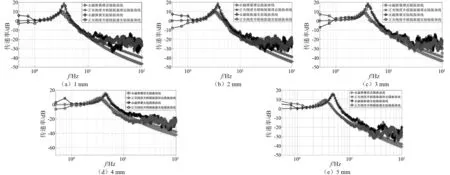
图18 永磁弹簧和正负刚度并联永磁隔振器内环形永磁体分别在1～5 mm处理论与实验传递率Fig.18 The comparison of the calculated and experimental transmissibilty of the PMS and MLVI with the inner ring in the range of 1 to 5 mm

图19 内环形永磁体在1～5 mm内永磁弹簧和正负刚度并联隔振器的实验固有频率Fig.19 Compared the natrural frequency of the PMS to that of the MLVI with the inner ring in the range of 0 to 5 mm

5 结 论

(1) 针对小负载使用隔振器的新需求，基于负刚度原理，提出了一种由橡胶带和永磁弹簧构成的正负刚度并联永磁隔振器的新构型。在Mooney-Rivlin的提出的橡胶本构关系模型的基础上，建立了橡胶拉力和刚度的数学模型，对该隔振器的隔振性能进行理论分析计算，并通过实验验证了采用该种方法进行隔振器的研究是有效的。

(2) 本文提出的正负刚度并联永磁隔振器的优点在于承载能力最大时，刚度最小，固有频率最低，隔振性能最好。此外，此项技术的深入研究的成果还可拓展应用到航空、航天和军事领域。

(A-1)

(A-2)

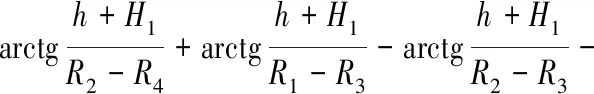
(A-3)

(A-4)

(A-5)

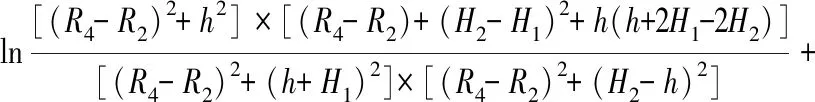
(A-6)

(A-7)

(A-8)