Watts-Strogatz型小世界发电机网络混沌振荡的有限时间混合控制
2019-08-31刘利花韦笃取
刘利花, 韦笃取, 张 波
(1. 广西师范大学 电子工程学院,广西 桂林 541004;2. 华南理工大学 电力学院,广州 510610)
随着工业化的快速发展,能源危机、环境污染问题越发突出。近年来,为减少化石燃料的污染和防止资源枯竭,各国政府大力发展风力发电[1-2]。风力发电的原理是通过叶片将风能转换为机械能,经过传动系统之后通过发电机将机械能转换为电能。目前主流变速风力发电机组主要有双馈感应发电机(Doubly Fed Induction Generator,DFIG)和直驱永磁同步发电机(Direct-Driven Permanent Magnet Synchronous Generator,D-PMSG)。D-PMSG因省去增速齿轮箱,减少了机械噪声,提高了可靠性,且有着制造成本低、速度快、高惯性力矩比、功率密度大、运行效率高等优点,被广泛应用于风力发电[3-5]。然而PMSG是一种多变量、强非线性系统,在某些参数及工作条件下会产生混沌振荡现象,主要表现为转矩、转速的间歇振荡、控制性能的不稳定、系统不规则的电磁噪声等[6-7]。混沌的存在使PMSG的输出功率产生大的振荡和波动进而影响电网的正常工作[8]。要使电网稳定运行则必须抑制PMSG的混沌振荡。
迄今为止学者们提出了大量的混沌控制方法并在各个不同领域得以运用。对于永磁同步发电机混沌控制,Hu等[9]提出了一种自适应非线性反馈控制器,抑制了含不确定参数PMSG系统的混沌现象;文献[10]利用执行依赖启发式动态规划原理抑制PMSG混沌行为并稳定地追踪最大功率值;Aguilar-Mejía等[11]用B样条神经网络方案控制PMSG系统混沌,并调节发电机的转子速率;文献[12]提出一种新型的非线性预测控制器能有效抑制PMSG的混沌振荡。上述控制方法主要针对单台PMSG,然而在实际发电系统中为了增大输出功率,会将多台发电机互联。由数量众多的PMSG连接成发电机网络,将使系统变得越来越复杂,进而对电网的稳定性和可靠性的要求也越来越高。因此,研究多发电机复杂网络的混沌行为,并且有针对性地提出相应的混沌控制策略,在保障电网的安全稳定运行方面具有重要的理论探索价值和实际应用参考价值。本文结合反馈控制和有限时间稳定性理论设计混合控制器,对WS(Watts-Strogatz)型小世界PMSG发电机网络进行混沌控制,使发电机网络在有限的时间内达到稳定状态,并通过有限时间稳定理论分析得到抑制发电机网络混沌的充分条件。在此条件下可以通过改变控制器参数,进而调节混沌控制的收敛时间。最后利用数值仿真验证理论分析结果的正确性和有效性。
1 WS型小世界D-PMSG网络模型
单台永磁同步发电机在d-q同步旋转坐标系下的状态方程为[13-14]
(1)
式中:id,iq和ω分别为d轴定子电流、q轴定子电流和转子角速度;Ld和Lq为d轴和q轴的电感;R为定子电阻;np为发电机转子的极对数;κ为永磁体的磁链;ud和uq分别为d轴和q轴定子电压;J为发电机组等效转动惯量;bm为转动黏滞系数;Te为电磁转矩;Tw为风力机的机械转矩。 其中电磁转矩Te为
Te=np(κiq+(Ld-Lq)idiq)
(2)
风力机的机械转矩Tw为
(3)
式中:pw为风力机吸收的机械功率;ρ为空气密度;R为风轮半径;Cp(λ,β)为风能利用系数;υ为输入风速;β为桨距角; ϑ为叶尖速比。
考虑均匀气隙永磁同步发电机即Ld=Lq=L, 经过无量纲变换后式(1)可变为
(4)
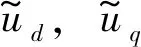
以式(4)为节点,构建N个节点的WS型小世界D-PMSG网络, 则第i个节点的状态方程为[15]
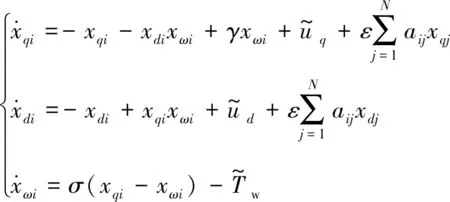
(5)
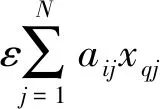
(6)
本文的WS型小世界发电机网络拓扑[16]构造过程如下:首先开始于一个含有N=100个节点的最近邻耦合环状网络,每个节点与左右相邻的各两个节点相连,然后以概率p随机重连网络中的每条边, 当p=0时是最邻近规则网络,p=1时是一个完全随机网络, 选取的p不同则对应的网络也不同。 图2描述的是p=0.6,ε=1.7时发电机网络任意一个节点的混沌现象。

图1 单台永磁同步发电机混沌吸引子Fig.1 Chaotic attractor of isolate PMSG
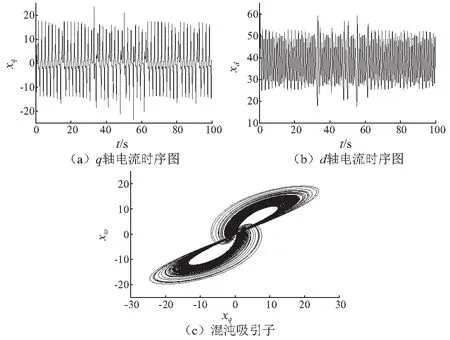
图2 发电机网络任意一个节点混沌现象Fig.2 Chaotic behavior of an arbitrarily node in motor network
当复杂发电机网络处于混沌时,发电机出现无规则的振荡,转速忽高忽低,这将增加滑环与电刷磨损程度,引起零部件或焊缝的疲劳、形成并扩大裂缝甚至断裂,甚至会引起发电系统的崩溃,因此必须研究WS型小世界发电机网络混沌振荡的控制方法。
2 复杂网络有限时间控制的预备知识
考虑一个由N个相同节点构成的线性耦合复杂网络,其一般形式为[17-19]
(7)

(8)
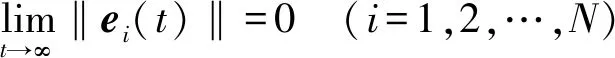
(9)
假设1[20]: 假设f(xi(t))满足单边Lipshitz条件,即对于任意的两个常数值y1,y2∈Rn, 存在一个大于0的常数αi和正定矩阵Γ使得式(10)成立
(y1-y2)T(fi(y1)-fi(y2))≤(y1-y2)TαiΓ(y1-y2)
i=1,2,…,N
(10)
定义1[21-22]: 如果存在一个常数T>0使得式(11)成立
(11)
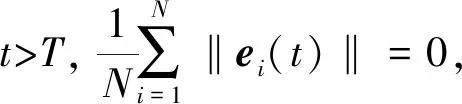
引理1[23-24]: 假设存在一个连续正定函数V(t)满足以下不等式
(12)
式中:σ>0,0<ρ<1, 那么对于任何初始时间t0,V(t)满足
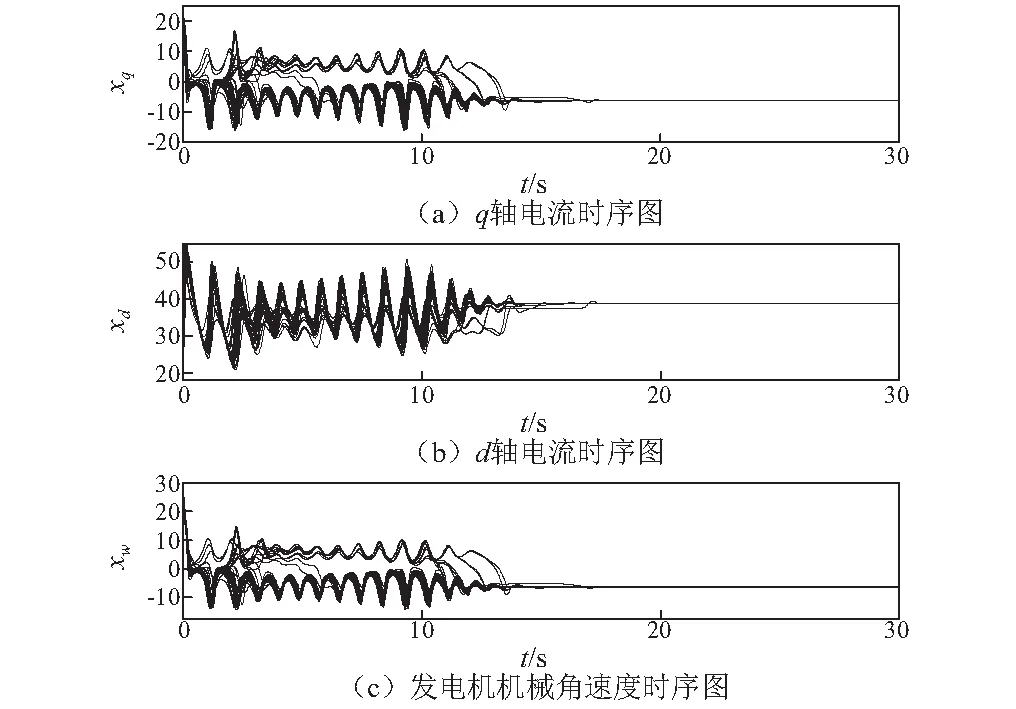
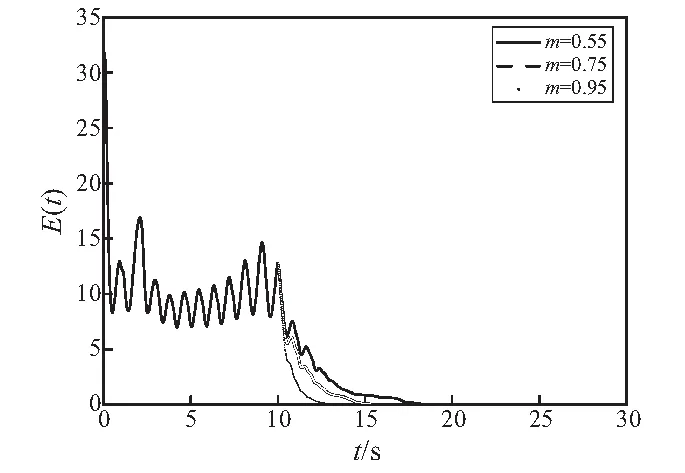
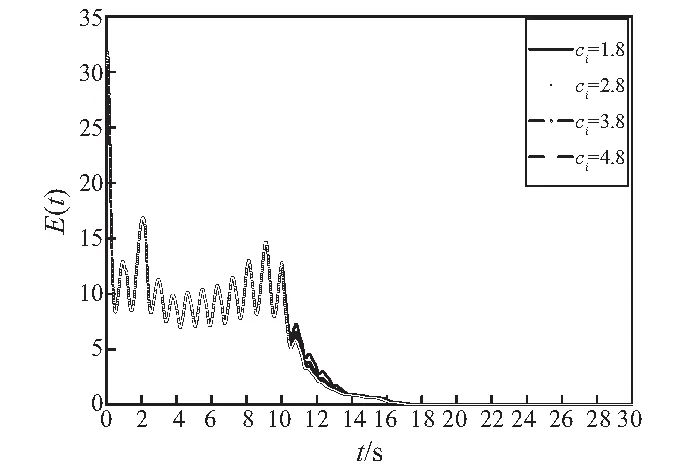
V1-ρ(t)≤V1-ρ(t0)-σ(1-ρ)(t-t0) (13) 和 V(t)≡0 ∀t≥t1 (14) 其中, (15) 引理2[25]: 对于任意实数li,i=1,2,…,n和实数p, 0 (16) 为了使WS型小世界发电机网络有限时间全局稳定。本文提出的控制器如下所示:对于‖ei‖≠0 (17) 而对于 ‖ei‖=0时ui=0 (18) 定义李雅普诺夫函数为 (19) (20) 根据假设1则式(20)可写为 (21) 则 (22) 所以由引理1可知发电机网络式(5)可在控制器式(17)的作用下,达到有限时间稳定,且控制时间t1的表达式为 (23) 由式(21)、式(23)可知,混沌控制时间与加入控制器时的状态变量xqi(t0),xdi(t0),xωi(t0)和控制器参数gi,ci及m有关,调节这些参数可改变抑制混沌的时间,其中gi越大网络混沌现象越快被抑制, 而ci只要满足上述条件便与收敛时间无关, 当gi,ci一定,V(t0)较大时则随m增大抑制混沌的时间收敛越快,V(t0)较小时m越大却收敛越慢。 图3 D-PMSG网络在第10 s加入控制器被控制到目标平衡点Fig.3 Control chaotic oscillations in D-PMSG network to goal equilibrium point while t0=10 s 为更好描述混沌D-PMSG网络控制情况,本文引入全局误差变量E(t)其表达式为 (24) 当E(t)=0说明D-PMSG网络全部节点都被控制到了目标平衡点。为了研究各个参数对D-PMSG网络混沌控制时间的影响,采用控制变量法逐个探究它们与混沌控制时间收敛的快慢关系,图4为保持gi=1.6,ci=1.8不变, 当m取0.55,0.75,0.95时全局误差变量时序图,由于本文选取加入控制器的时刻的状态变量与目标平衡点的误差较大,则V(t0)也会比较大, 所以该图显示m越大D-PMSG网络混沌越快被控制。 图5为保持ci=1.8,m=0.6不变, 当gi取1.6,2.6,3.6,4.6时全局误差轨迹图,由图5可知,gi越大,混沌控制时间越快收敛。图6为保持gi=1.6,m=0.6不变, 当ci取1.8,2.8,3.8,4.8时E(t)曲线图,由图6可知,随ci增大,控制D-PMSG网络混沌的时间几乎没有变化。这些结果进一步验证了之前理论的正确性。 图4 全局误差曲线图(gi=1.6,ci=1.8,m=0.55,0.75,0.95)Fig.4 Trajectories of global error with gi=1.6,ci=1.8,m=0.55,0.75,0.95 图5 全局误差曲线图(ci=1.8,m=0.6,gi=1.6,2.6,3.6,4.6)Fig.5 Trajectories of global error with ci=1.8,m=0.6,gi=1.6,2.6,3.6,4.6 图6 全局误差曲线图(gi=1.6,m=0.6,ci=1.8,2.8,3.8,4.8)Fig.6 Trajectories of global error with gi=1.6,m=0.6,ci=1.8,2.8,3.8,4.8 研究了以D-PMSG为节点的WS型小世界发电机网络混沌控制问题。 (1) 结合反馈控制和有限时间稳定性理论设计了混合控制器,不仅能使整个混沌D-PMSG网络控制到目标平衡点,还能使全部节点在有限的时间内达到稳定状态。 (2) 利用有限时间稳定性理论得到了D-PMSG网络混沌控制的充分条件,通过改变该控制器的参数,调节混沌控制时间的收敛速度,避免了D-PMSG网络混沌控制时间过长的难题。 (3) 利用数值仿真验证了该控制策略的正确性和有效性。 研究结果对保证复杂发电网络的稳定运行可望提供有价值的参考和新见解。
t0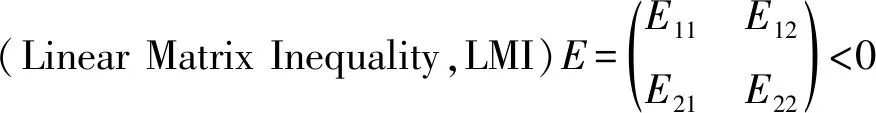

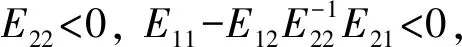
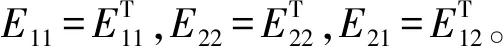
3 有限时间PMSG混沌控制器设计

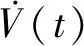
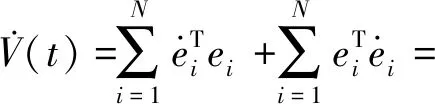
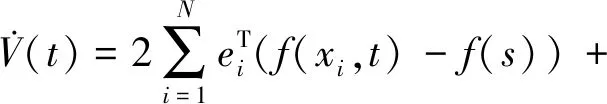
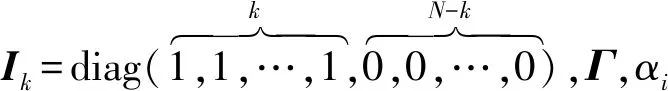
4 数值仿真与分析
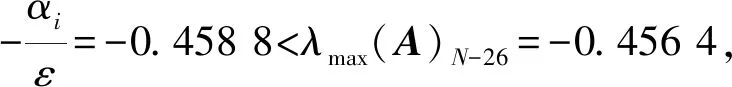

5 结 论
