EWT和ICA联合降噪在轴承故障诊断中的应用
2019-08-31吕跃刚何洋洋
吕跃刚, 何洋洋
(华北电力大学 控制与计算机工程学院,北京 102206)
旋转机械早期故障信号能量小、信噪比低,特征信息往往湮没在嘈杂的背景噪声中,导致低频段故障频率及倍频极其微弱,严重影响诊断效果。要实现强噪声背景下旋转设备状态特征的准确提取,需对振动信号进行降噪处理。
传统滤波方法通常使用滤波器设置不同的通带,本质上是利用滤波器的幅值响应函数对于不同频率的信号具有不同程度的幅值传递响应。仅适用于信号和噪声处于不同频带的情况。而实际变工况条件下的振动信号,和干扰噪声在频带上经常发生混叠,使得传统滤波方法效果不佳。
独立分量分析(Independent Component Analysis,ICA)是基于高阶统计分析理论的冗余取消方法,其通过观测到的多个混合信号重构独立源信号,不受强干扰噪声的影响,适用于潜在及早期微弱信号提取。但ICA提取方法要求观测信号数目大于或者等于信号源数目,不适用于工程中常见的单通道欠定情况。
解决欠定盲源分离的方法是将信号分解后引入虚拟噪声通道,将一维观测延伸为多维观测。文献[1]将经验模态分解法(Empirical Mode Decomposition, EMD)与ICA相结合,将观测信号EMD分解后利用ICA方法提取源信号。由于EMD方法存在的模态混叠和端点效应等问题,未能达到理想降噪效果。文献[2]与文献[3]分别引入了集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)与局部均值分解(Local Mean Decomposition, LMD)代替EMD产生单通道的虚拟噪声通道,改善了由于模态混叠导致的去噪不完全现象。但由于EEMD和LMD采用递归的分解方式,受采样频率影响,分解误差较大,降噪效率低。文献[4]提出基于变分模态分解(Variational Mode Decomposition, VMD)和ICA联合降噪的方法。VMD非递归、变分模态的分解方式有效避免了EMD固有的模态混叠缺陷,提高了降噪效果,但其效果依赖于模态数K、二次惩罚因子α及双重上升的时间步长τ的设定,不能实现自适应滤波降噪。
本文提出经验小波变换(Empirical Wavelet Transform,EWT)和ICA联合降噪的方法(EWT-ICA),获得了更好的稳定性和信噪分离效果。本文讨论该方法的基本原理和实现步骤,研究其在实际轴承振动信号降噪和故障诊断中的应用。
1 EWT-ICA联合降噪基本原理
1.1 经验小波变换基本原理
EWT是在EMD的基础上,结合小波分析的概念,提出的多分量信号分解方法。具有理论充分、自适应性好、计算量小的优点,且不存在模态混叠。其实质是对信号频谱进行自适应分割,建立合适的小波滤波器组,加小波窗后提取紧支撑傅里叶频谱的调幅-调频(Amplitude Modulation-Frequency Modulation, AM-FM)成分 ,即固有模态函数(Intrinsic Mode Function,IMF)
(1)
首先,对傅里叶谱进行自适应划分。信号的傅里叶支撑[0,π]被分割成N个带宽不等的频带Λn,各频带边界ωn取为信号傅里叶谱相邻极大值的中点,可表示为
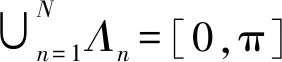
(2)
以各ωn为中心,定义一个宽度Tn=2τn的过渡段,如图1所示阴影区。
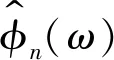

图1 傅里叶轴分割图Fig.1 Partitioning of the Fourier axis
(3)
(4)
其中,τn与β(x)可表示为
(5)
(6)
(7)
最后,可得原信号重构为
(8)
式中:*为卷积运算。EWT分解所得固有模态函数fi定义为
(9)
(10)
1.2 独立分量分析基本原理
ICA为基于高阶统计信息的特征提取方法,具有很强的盲辨识能力和特征提取能力。设M维观测向量X=[x1,x2,…,xM]T,可表示为N维独立源向量s=[s1,s2,…,sN]T的线性组合形式
x=As
(11)

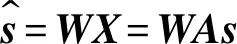
(12)
将ICA方法应用在机械故障诊断中,信噪分离时既不受频带混叠的影响,又能实现复杂工况的强噪声消噪,相比传统自适应滤波,稳定性与滤波效果更好。但传统ICA方法要求观测向量数目大于等于源向量的数目,不适用于工程中常见的单通道盲源分离,须引入虚拟噪声通道,将一维观测延伸为多维。
1.3 峭度及相关系数准则
峭度K反映振动信号中的冲击成分的比重,适用于表面损伤类故障,尤其是早期故障的诊断。峭度值越大,说明其含有的故障冲击成分越多,故障越严重。
(13)

相关系数反映变量x,y之间的相关关系密切程度。各IMF相关系数rxy的绝对值越大,其与原始信号的相关程度越高,可降低振动信号中非相关量的干扰。
(14)
考虑旋转机械振动信号的特殊性,取峭度和相关系数具有相同权值,综合峭度对故障冲击的敏感度和相关系数对干扰噪声的敏感度,剔除峭度和相关系数联合最优的前几个IMF分量,再将其余分量重构,引入虚拟噪声通道。
1.4 EWT-ICA联合降噪方法研究
EWT虽避免了模态混叠,且计算量小、鲁棒性强,具有较好的模态分解和特征提取能力,但仅使用EWT算法,盲目取舍模态函数,可能导致故障特征信息提取不完全。经典的ICA算法虽不易受强噪声干扰,但是只能应用于超定盲源分离问题。而机械振动信号往往是单通道的一维加噪观测,不满足ICA适用条件。
为了发挥EWT与ICA信号处理的优势,弥补各自不足,本文提出了EWT与ICA联合降噪方法。通过EWT引入噪声信号,包含了轴承振动信号的先验信息,避免了因引入噪声不当而造成的信噪分离效果差的问题。同时,观测信号与虚拟噪声通道信号共同作为ICA的输入矩阵,有效解决了ICA欠定盲源分离的问题。算法流程图,如图2所示。

图2 EWT-ICA联合降噪流程图Fig.2 The flowchart of the EWT-ICA noise reduction method
EWT-ICA具体实现步骤如下
步骤1通过EWT对轴承振动信号进行分解,得到若干固有模态函数IMF;
步骤2计算各IMF的峭度值和相关系数,剔除与原始信号相关程度较高、冲击成分比重较大的模态函数,构建虚拟噪声通道信号;
步骤3利用FastICA算法,同时对观测信号和虚拟噪声信号进行解混,得到源信号的最佳估计信号;
步骤4对步骤3得到的信号进行Hilbert包络解调,提取轴承故障频率,进行故障诊断。
2 诊断实例分析
本文选用Case Western Reserve University公开的滚动轴承故障模拟平台数据,风扇端采用 SKF6205型深沟球轴承,其关键参数如表1所示。
采用电火花加工技术,在轴承内圈布置直径为0.177 8 mm,深度为0.279 4 mm的单点损伤,电机负载0.735 kW,转速n为1 772 r/min,采样频率12 000 Hz。根据经验式(15)、式(16)可得转频fr为29.53 r/s,内圈故障特征频率fic为159.93 Hz。
(15)

(16)
当轴承内圈发生表面损伤类故障时,滚动体经过损伤点,会产生突变的冲击脉冲力,产生低频振动成分的同时,诱发轴承的高频固有振动成分。如图3所示,故障信号的时域图中存在明显的周期性冲击,采用传统的频谱分析方法,故障频率及其倍频淹没在噪声中难以辨识,需降噪处理。本文采用EWT-ICA方法,从信号分解和信号去噪两方面,对比EMD-ICA与EEMD-ICA方法,验证其有效性与优越性。

图3 早期故障信号时域、频域波形Fig.3 Time-domain and frequency-domain waveforms for early fault signals
2.1 信号分解对比
2.1.1 EMD分解效果
EMD在分解过程中,由于脉冲干扰和噪声带来的信号极值点的异常分布,终止条件设置不合理,导致上、下包络的时间尺度不一致,具有模态混叠和虚假模态现象。EMD分解故障信号共获得13个IMF,篇幅所限,本文仅列出前五阶分解结果。IMF1几乎覆盖了整个频率范围,且IMF3与IMF4之间的模态混叠明显,如图5所示[5-7]。

图4 EMD前五阶模态分量Fig.4 The first five modal components with EMD
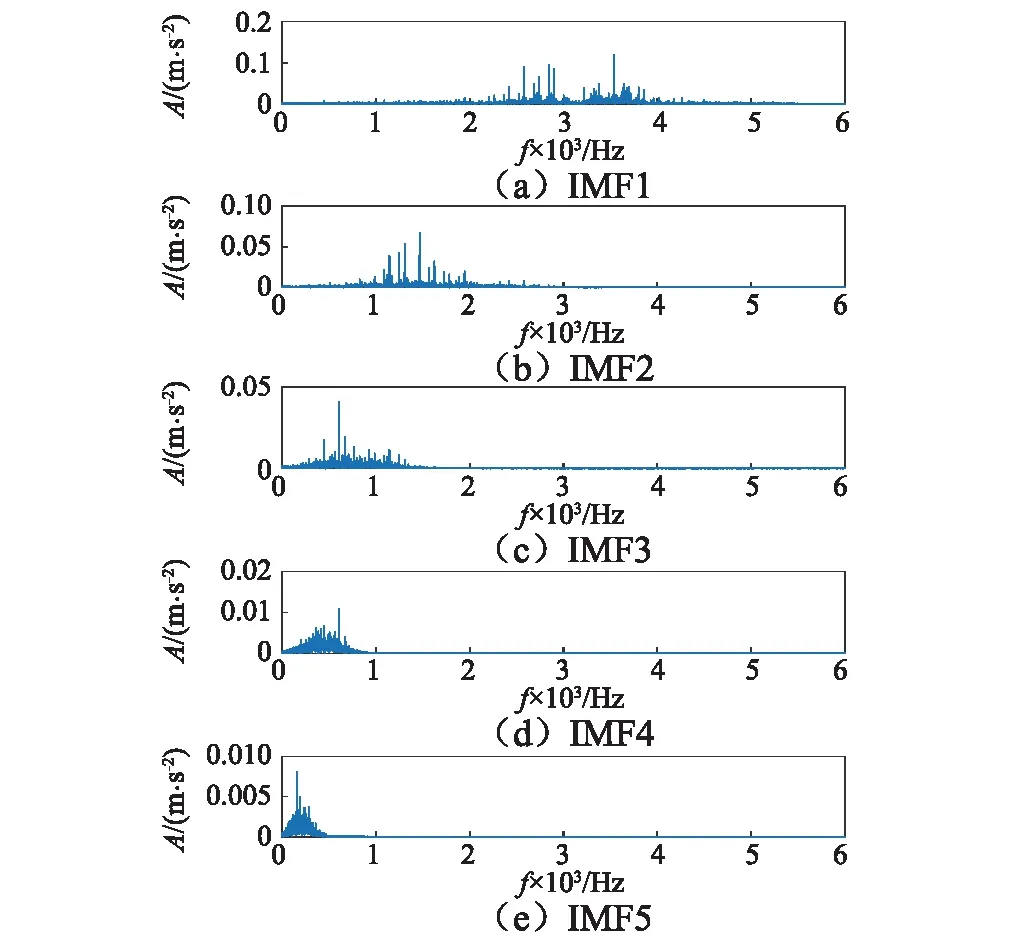
图5 EMD分解前五阶模态分量频谱Fig.5 Spectrum of the first five modes with EMD
2.1.2 EEMD分解效果
参考文献[8]中EEMD参数设定方法,取总体平均次数为100,白噪声幅值标准差比值系数为0.15(0.5倍信号标准偏差),获得与EMD相同数目的IMF。EEMD前五阶的分解时域及频域波形,如图6、图7所示。
由频谱分解结果,EEMD因加入随机高斯白噪声序列平滑脉冲干扰,改善了EMD固有的模态混叠现象,但低频段的分离效果仍不明显。且由于进行多次平均运算抵消白噪声,分解效率较低。
2.1.3 EWT分解效果
经验小波变换的实质是利用信号在频域的稀疏性,在傅里叶频谱[0,π]范围内对信号划分,建立5个合适的小波滤波器。信号频谱及各滤波器检测到的支撑边界,如图8所示。傅里叶支撑的连续边界划分,取信号傅里叶谱中相邻极大值的角频率Ωn,Ωn+1的中点,为各连续部分频带边界角频率ωn,各带通滤波器的上、下截止频率分别为ωn+1与ωn。其中,ω0=0,ωN=π。确定其在傅里叶轴的分割区间,如图9所示。加小波窗后进行模态分解,结果如图10、图11所示。

图6 EEMD前五阶模态分量Fig.6 The first five modal components with EEMD

图7 EEMD前五阶模态分量频谱Fig.7 Spectrum of the first five modes with EEMD
对比EMD与EEMD的分解结果,有以下结论:
(1)EWT分解模态数明显少于EMD与EEMD,这与EWT在频域内寻找函数最大值,以此自适应划分各IMF支撑边界有关。该方法具有完备小波理论支撑,避免了EMD与EEMD存在的虚假模态问题,提高了信号分离的可靠性。

图8 故障信号频谱及支撑边界Fig.8 Spectrum of the fault signal and supporting boundaries

图9 故障信号傅里叶轴分割Fig.9 Fourier axis segmentation of fault signals
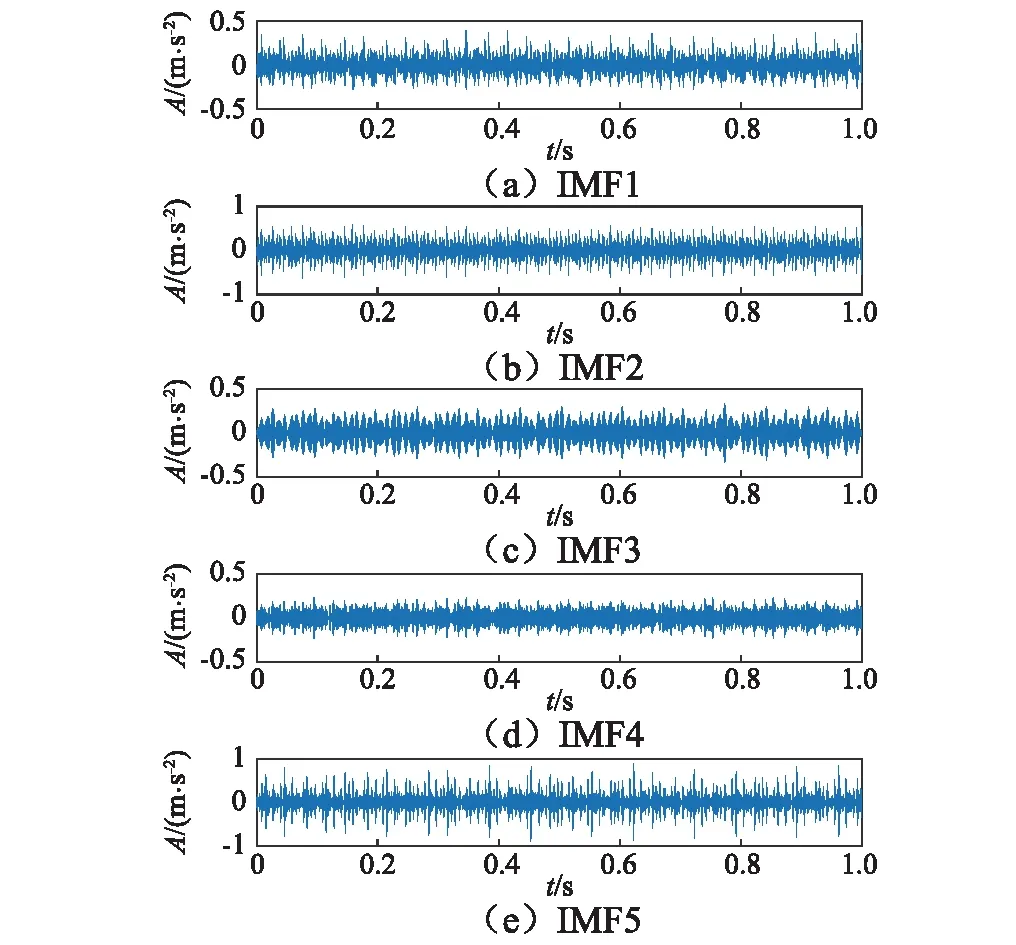
图10 EWT分解各IMF分量Fig.10 Each IMF components resulting with EWT
(2)EWT模态函数在各个频段的分离效果明显,消除了模态混叠和端点效应,避免信号中的间断、干扰和噪声等异常部分的引入,具有较强的鲁棒性。
(3)相比EEMD牺牲运算时间,频繁加入白噪声进行总体平均运算,EWT利用了时域信号的频域稀疏性,在具有良好分解效果的同时,运算量远小于EEMD。

图11 EWT分解各IMF分量频谱Fig.11 Spectrum of each IMF with EWT
2.2 信号去噪效果对比
2.2.1 构造虚拟噪声通道
EWT分解后各IMF分量的峭度及相关系数如表2所示。采用峭度及相关系数准则,一方面,使用峭度衡量故障特征信息的比重,表征轴承故障的严重程度;另一方面,考虑相关系数,用于剔除模式分解中的高频噪声和低频虚假分量,提高分解结果的可靠性。由表2可知,IMF2与IMF5的峭度和相关系数最大,保留了最多真实的故障信息,故将其余分量求和,构建虚拟噪声通道。

表2 EWT分解效果对比
同理,结合表3与表4,综合峭度和相关系数指标,分别构建EMD与EEMD的虚拟噪声通道,作为ICA算法的输入矩阵。

表3 EMD分解效果对比

表4 EEMD分解效果对比
2.2.2 降噪结果分析
将原始信号加入虚拟噪声通道,作为ICA的输入矩阵,解混后得到估计的有用信号和噪声信号。然后对有用信号进行短时傅里叶变换(Short-Time Fourier Transform,STFT),采用时频分析的方法,同时从时域和频域观察信号的能量密度,能量时频图纵坐标标度“倍频X”为轴承故障频率fic。
图12和图13所示的时域图与时频图定性地反映了三种方法的降噪效果,结合表5,从定量角度进行对比,有以下结论:

表5 各方法降噪效果对比
(1) ICA方法可有效的从混合信号中分离出有用信号,但由于其没有任何源信号的先验知识,所分离信号的排列顺序具有不确定性,需根据时域波形及信噪比等评价指标确定;所分离信号的幅值具有不确定性,但并不影响对故障信号的特征识别。
(2)对比EMD-ICA和EEMD-ICA所分离源信号时域图,两者局部波形较为振荡,受模态混叠影响,抑制脉冲干扰能力不足;而EWT-ICA降噪后的时域波形更平滑,冲击脉冲的规律性更明显,受噪声干扰较小。

图12 各方法降噪时域波形图Fig.12 Time domain waveforms of noise reduction results using each method

图13 各方法降噪能量时频图Fig.13 Time-frequency spectrogram of noise reduction results using each method
(3)由表5可知,EWT-ICA方法降噪后信号的峭度值最高,说明该方法保留了较为完整的障特征信息;相关系数最大,表明该信号与原始信号的相似程度高,异常噪声影响小;信噪比最高,显示了良好的去噪能力,同时该方法还兼具良好的去噪效率。
(4)EMD-ICA因分解了过多虚假模态,所分离源信号的频率分布比较凌乱,噪声干扰明显;EEMD-ICA源信号在四倍故障频率(4X)以上,干扰噪声的幅值增加,与各倍频发生混叠。而EWT-ICA所分离源信号在各倍频处的能量相对集中,层次清晰地突出了带有故障特征信息的周期性冲击。
2.3 故障信号诊断
对EWT-ICA方法所得源信号进行包络解调,如图14所示。从图14可知,轴承内圈故障特征频率fic(160 Hz)及其倍频,且幅值明显。同时59 Hz处幅值突出,对应了二倍转频2fr。由此可判断轴承的内圈故障,证明了本文方法的可靠性[9-12]。

图14 源信号包络频谱图Fig.14 Envelope spectrum of source signal
3 结 论
针对强噪声中微弱故障特征提取的问题,本文提出EWT和ICA联合降噪方法,并将其应用于轴承故障诊断中。通过对仿真和实测振动信号的分析,验证了本文方法的有效性和优越性,结论如下:
(1)EWT通过自适应傅里叶频谱分割,具有完备小波理论支撑,不仅提高了分解速率,还克服了EMD和EEMD存在的模态混叠和端点效应导致的噪声残留、特征信息丢失等问题。
(2)仅使用EWT降噪方法,盲目取舍模态函数,可能导致重构信号中部分故障特征丢失。结合ICA算法,使其既不受信噪分离时频带混叠的影响,又能避免噪声幅值大于振动信号幅值的影响。
(3)依据峭度和相关系数准则选择模态函数,兼具稳定性和对故障的敏感性;同时引入虚拟信号通道,有效解决了ICA算法欠定盲源分离问题,避免了因盲目引入噪声分量导致降噪效果不佳的影响。
(4)EWT-ICA联合降噪方法,对于工况复杂的强背景噪声分离效果明显,理论上适用于各种类型信号,对于弱信号的检测和提取具有重要意义。
