6 520 TEU集装箱船船体温度变形
2019-08-31杜金纬
纪 玮, 陈 震, 杜金纬
(上海交通大学 海洋工程国家重点实验室, 上海 200240)
0 引 言
在船舶建造过程中,船体质量、焊缝收缩、温差等因素通常会使船体产生变形。过大的船体变形会导致轴系校中不准,产生振动噪声,影响推进效率[1-2]。绘制船舶水线时须考虑变形引起的船舶基线变化,否则可能导致水尺勘划不准确,影响船舶排水量、稳性等静水力性能[3-4]。过大的船体变形甚至还会造成船体构件因受力过大而发生屈服破坏。因此,在船舶设计和建造过程中,准确预估船体变形大小并采取有效的控制措施是保障船舶建造质量和安全的重要方面。
温度是引起船体变形的重要因素,当船舶处于有温差的环境中时,船体剖面内非线性的温度分布会使船体梁发生温度弯曲变形。日照温度变化使船体结构的不同部分迅速产生不均匀的温度分布,在很短时间内形成相当大的温差,从而产生很大的温度变形[5]。在估算船体变形时,日照温度变化是一项不能忽视的重要因素。
以某6 520 TEU集装箱船为例,基于二维稳态热传导和薄壁梁理论,计算船体剖面内的温度分布和船体梁变形,讨论中国不同区域和季节的船体温度变形大小和特点,并分析日照因素对船体变形的影响。
1 研究方法
船体温度变形可采用三维有限元方法进行求解[6],建立船体结构有限元模型,根据环境温度条件和热源输入,计算船体结构的温度分布和应力变形。三维有限元法的求解精确度高,但由于建模过程繁琐、所需参数较多等,难以实现快速预估船体变形大小,因此并不适用于船舶设计初期。
本文提出船体温度变形快速预报方法[7],将船体简化为一根变剖面的薄壁梁,通过二维热传导理论计算船体剖面的温度分布,根据受约束平板温度应力原理和梁弯曲有限元法求解船体变形,精度可满足船舶初期设计的需要。
1.1 船体梁的离散
将船体离散为一根变剖面的阶梯形薄壁梁,沿船长方向划分若干个单元,每个单元剖面取该段船体中部的剖面形式。假设每个船体梁单元的温度分布沿船长方向保持不变,此时可将温度分布简化为二维稳态热传导问题。针对每一个船体梁单元,将剖面离散成若干个温度构件,构件相交处为温度节点,采用热传导理论可求解船体梁单元剖面的温度分布。在此基础上,仅考虑因温度变化引起的弯曲,认为船体上无其他外力作用,温度变化将产生船体梁单元等效节点力和力矩,船体梁在此载荷作用下产生弯曲和收缩变形。船体温度变形快速预报方法的计算流程如图1所示。
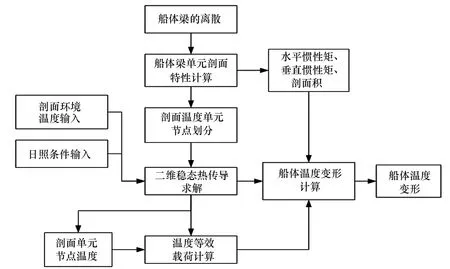
图1 计算流程
1.2 船体结构温度求解
将每个船体梁单元的剖面结构离散为若干个温度单元,忽略船体纵骨、扶强材等支持构件,只保留纵向贯穿的船体板构件,由温度单元表示船体板构件,在船体构件相交或板厚变化处设置节点。典型船体剖面温度单元划分如图2所示。
采用热传导理论求解船体剖面的结构温度。假设温度沿板厚方向保持不变,对于图3所示温度微元,热流平衡条件为
dQ1+dQ2+dQ3-dQ4=0
(1)
式中:dQ1和dQ2分别为左侧和右侧导热层的导热量;dQ3和dQ4分别为温度单元内部流入和流出微元的导热量。
考虑微元表面对流换热、环境热量流入流出和微元热流平衡,最终可得温度微元热传导微分方程为

(2)


图2 船体剖面温度单元划分

图3 热传导微元
对于与多个单元相连的节点,在该节点处流入所有这些单元的热流量总和应为0,可列出该节点的热流平衡方程,通过联立求解方程组得到船体剖面的温度分布。
1.3 船体温度变形计算
根据受约束平板温度应力原理,将船体剖面温度载荷转化为船体梁弯曲等效节点力和力矩,等效节点力仅由温度分布不均匀产生,大小为阻止船体产生变形所需要施加的附加力和力矩,即船体梁单元载荷列阵为
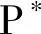
(3)

得到刚度矩阵和载荷列阵后进行约束处理,即可求出船体梁的位移。
根据以上原理编写MATLAB程序,求解不同环境条件下船体结构温度分布和船体梁水平弯曲、垂直弯曲及轴向收缩变形。
2 计算模型
2.1 计算对象
选取6 520 TEU集装箱船为研究对象,该船的主尺度参数如表1所示。将船体沿船长方向等间距划分成10段船体梁单元(端面划分如图4所示),以各船体梁单元中部位置的剖面形式表示该单元剖面,组成阶梯形薄壁船体梁模型。

表1 船舶主尺度参数
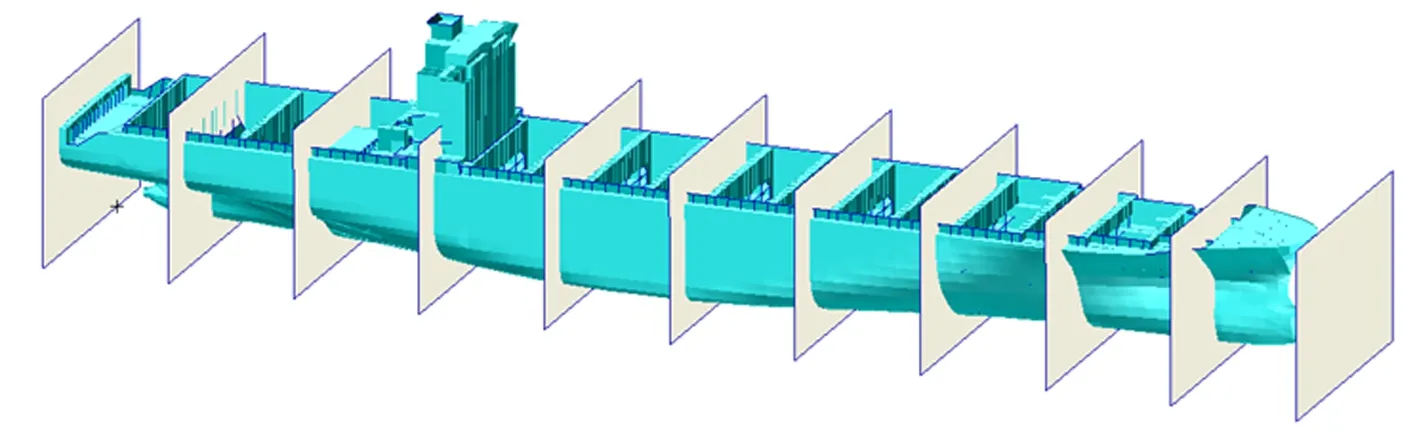
图4 6 520 TEU集装箱船模型
2.2 计算工况
针对6 520 TEU集装箱船在大连、上海、广州等3个地区的夏季和冬季的船体温度变形进行分析。3个地区气温、水温值如表2所示,其中气温数据来源于国家气象数据共享服务平台中国地面气温日值0.5°×0.5°格点数据集,选取该地区夏季7月份最高气温和冬季1月份最低气温。由于水的比热容较大,水温相较气温而言变化较小,因此水表面温度值近似选取当月气温的月平均值。

表2 3个地区气温和水温数值 ℃
根据文献[8]的渤海、黄海、南海近岸等3个断面横切海水温度,并结合船舶吃水深浅,分析得出夏季水面与船底处的水温温差约3~5 ℃,冬季水温在船舶吃水范围内均匀分布[9]。3个地区夏季、冬季环境温度如图5所示,上海地区船中剖面温度单元、节点、环境温度情况如图6所示。初始环境温度取20 ℃。
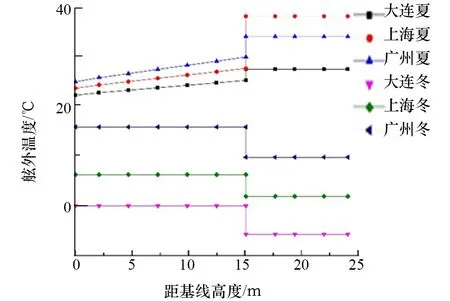
图5 3个地区夏季冬季环境温度

图6 船中剖面温度计算模型
3 温差变形分析
3.1 同一区域不同季节船体变形比较
图7和图8分别为大连、上海和广东等3个地区夏冬两个季节的船体垂向温度变形。由图7和图8可见,在同一个地区,夏季和冬季船体温度变形相反,夏季船体中部向上拱起,艏艉两端向下,呈中拱状态,而冬季船体温度变形呈中垂状态。这是由于水的比热容比空气大,夏季水温低于气温,冬季水温高于气温,使两个季节的温度变形呈相反的状态。
夏冬两个季节由温差引起的船体变形大小差异很大。在夏季,上海地区由温差引起的变形最大,达到60.7 mm,广州地区最大变形仅为上海的一半,大连地区变形最小;冬季3个地区船体温度变形相差较小,最大相差6.8 mm。从同一地区不同季节来看,上海地区夏季变形量约为冬季变形量的3倍,大连和广州地区的变形量相当。3个地区船体温度变形最大值如表3所示。

图7 3个地区夏季船体温度变形
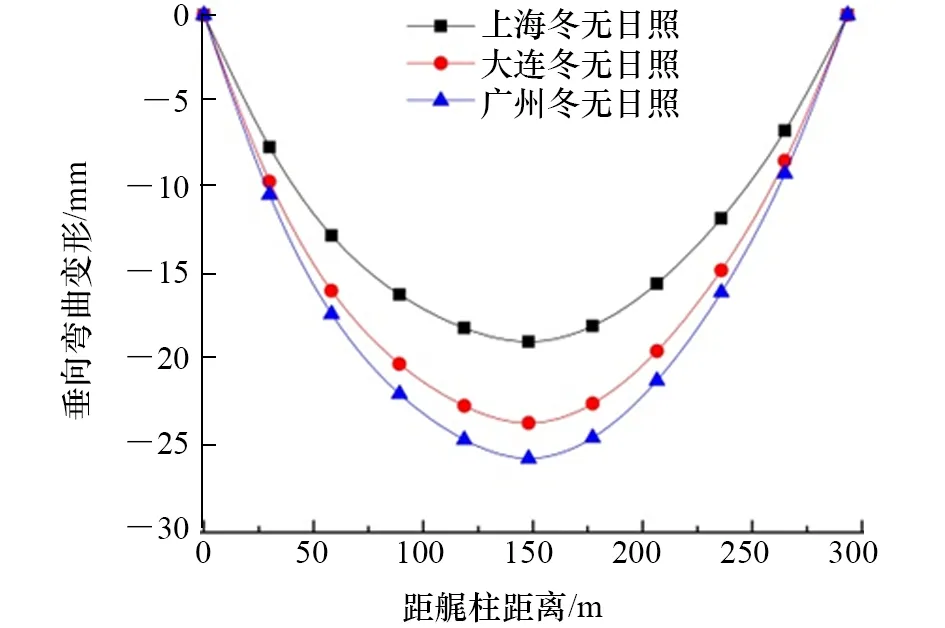
图8 3个地区冬季船体温度变形

表3 3个地区夏冬两季船体变形挠度最大值 mm
3.2 日照对船体弯曲变形的影响
日照条件是影响船体变形的重要因素,日照辐射使船舶表面局部快速升温,由此产生较大的温度应力和变形。在计算受日照时的船体结构温度时,在相应的温度单元外侧施加日照辐射热流密度,并根据热传导理论计算船体结构单元温度[10]。
本文算例6 520 TEU集装箱船的设计结构吃水为14.0 m,受日照的部位为舷侧水线以上部分。图9为3个地区夏季受日照时的船体温度变形,由图可见,日照条件对船体变形影响很大,上海地区受日照的船体变形达121.9 mm,约为无日照时船体变形的2.0倍,广州、大连地区受日照时的船体变形分别为无日照时船体变形的2.9倍和3.7倍。这是由于在夏季日照辐射可使船体表面升温达20~30 ℃,水线上下船体结构的温差增大,相应增加了船体剖面温度梯度所致。

图9 夏季无日照和双侧日照挠度变形
3.3 不均匀日照对船体弯曲变形的影响
由于日照角度的变化,船体表面可能只有一侧受到日光照射,此时船体除了发生垂向弯曲变形外,还将发生水平弯曲变形。图10为大连、上海、广州等3个地区夏季船舶受到单侧日照时垂向弯曲变形和水平弯曲变形。单侧受日照时船体垂向弯曲变形为91.3 mm,约为双侧受日照时变形量的75%,水平弯曲变形为23.2 mm。广州、大连单侧受日照时的水平弯曲变形值分别为22.4 mm和18.5 mm,垂向弯曲变形值也较双侧受日照时有所减小。不均匀日照产生的船体水平弯曲变形量虽不大,但与垂向弯曲变形耦合叠加,则使船体变形状态更为复杂。

图10 3个地区夏季单侧日照挠度变形
3.4 船体纵向变形
温度变化还将引起船体的纵向收缩和伸长变形,表4为大连、上海和广州等3个地区夏冬两季的船体纵向变形值。上海夏季无日照时船体纵向伸长量为40.4 mm,双侧日照时为53.1 mm,冬季收缩量为-52.9 mm;广州夏季船体伸长量和冬季收缩量均小于上海,大连夏季伸长量最小,但冬季收缩量最大,达-75.8 mm。船体纵向收缩和伸长变形规律与初始环境温度大小有关,本文计算的初始环境温度为20 ℃:大连冬季气温为-5.7 ℃,与初始环境温度温差最大,因此船体纵向收缩量也最大;大连夏季气温为27.5 ℃,与初始环境温度相差最小,因此船体纵向收缩量也最小。

表4 大连、上海、广州等3个地区船体纵向变形 mm
4 结 论
基于稳态热传导和薄壁梁理论,分析6 520 TEU集装箱船的船体温度变形,针对大连、上海、广州等3个地区在夏季和冬季时的环境条件,计算比较船体因温差引起的弯曲变形和纵向变形,主要得到以下结论:
(1) 船体温度变形在夏季和冬季呈相反趋势,夏季船体呈中拱变形,冬季船体呈中垂变形。
(2) 日照辐射会使船舶表面升温,增加船体剖面温度梯度,上海地区考虑日照因素时的船体温度变形达121.9 mm,约为无日照时的2倍,其他地区日照引起的船体变形也显著增加。
(3)初始环境温度为20 ℃时,上海夏冬两季节的温差引起船体纵向变形分别为40.4 mm和-52.9 mm,大连地区冬季船体纵向收缩量最大,为-75.8 mm。
