一种液体火箭发动机试验台螺纹拧紧力矩量化控制方法
2019-08-31马军强李志刚宋振龙
马军强 李志刚 宋振龙 蒋 宇
(北京航天试验技术研究所,北京100074)
1 引言
在液体火箭发动机地面试验安装工艺中,球头-锥面螺纹连接形式的装配数量最多,如图1所示。球头-锥面螺纹连接件的密封性对整个试验的成功与否起着至关重要的作用。
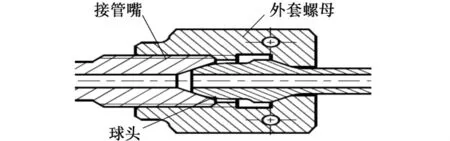
图1 球头-锥面螺纹连接件剖面图Fig.1 Cross-sectional view of ball-cone threaded
在安装工艺中,操作员施加的拧紧力矩转化为夹紧球面和锥面的贴合力,该贴合力促使球头面和锥面相互压紧,形成密封面[1]。传统的液体火箭发动机试验台螺纹安装工艺对拧紧程度没有量化控制要求[2],拧紧度的保证靠经验拧紧和气密检查,具体流程为:
(1)操作员凭经验拧紧所有的螺纹连接件;
(2)对可密封管路静态增压0.5MPa的氦气,借助氦质谱检漏仪或肥皂泡对连接部位进行气密检查。
上述拧紧度保证方式存在“未拧紧”或“过拧紧”的可能。如果螺纹连接处“未拧紧”,在发动机恶劣的试验工况下可能会导致个别部位连接失效,如螺纹松弛或者密封腔泄漏。如果螺纹连接处“过拧紧”,可能会对发动机或者试验台螺纹对接口造成压痕[3],影响发动机产品质量或者螺纹连接件寿命。
鉴于上述装配可靠性提升的需求,本文通过统计学理论和试验验证方法探索了试验台上装配数量最多的三种规格的球头锥面螺纹连接件(M12×1.25、M14×1.5和 M16×1.5,材质 1Cr18Ni9Ti)力矩量化控制的数值范围和方法,确定了适用于液体火箭发动机试验台的螺纹拧紧力矩量化控制工艺方法,该方法对提高液体火箭发动机试验的可靠性具有重要作用,也可推广应用于其他工程领域螺纹拧紧力矩量化控制中。
2 力矩量化范围的确定与分析
2.1 力矩值统计
2.1.1 在非发动机试验环境下,对同一规格,同一材质的球头-锥面螺纹连接件进行多人次、重复性的力矩测量,记录力矩值。采用这种方法的原因一是克服不同人员操作带来的力矩测量值统计偏差;二是在非发动机试验环境下,可克服试验工艺装配时的空间局限,保证力矩测量值的客观准确性。
2.1.2 在实际发动机试验环境下,对同一规格、同一材质的球头-锥面螺纹连接件进行单人、多次、非重复性的力矩测量。采用这种方法,一是因为实际的发动机试验具有一定风险性,工艺规程要求定编定岗,在试验系统上进行的力矩量化操作不具有多人次、重复性测量的条件;二是在试验系统上施加的力矩值经过了试验的考核,力矩值的准确性会更客观。
2.2 基于1σ准则的力矩值分析
无论是在哪种统计环境下,操作者所获得的力矩样本都会受到各种物理因素的影响,致使样本数据中混有离群值。如果离群值参与统计分析计算,会影响施加的力矩值的客观可靠度。因此,采取某种方法剔除离群值会大大减小人为测量误差,使统计结果更符合客观事实。1σ准则是进行数据统计分析的有效方法。
设对被测量X作n次独立测量,得到的测量样本为x1,x2,……,xn,则其平均值为
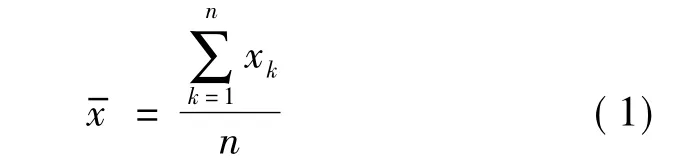
测量样本的残差vk和实验标准差s(xk)则可表示为
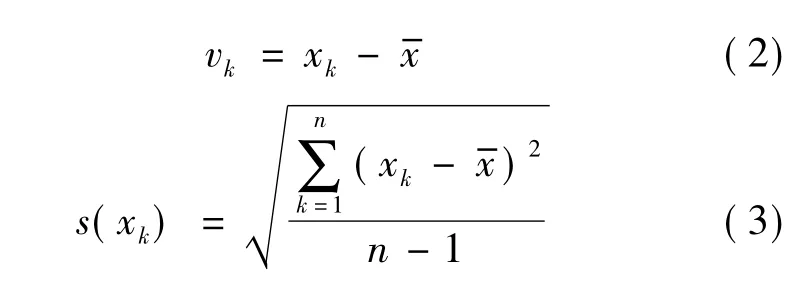
在正态分布下,随机误差的绝对值超过1倍实验标准差的概率很小,可以认为是极小概率事件,故当时可认为该测量子样属于离群值应予剔除。按1σ准则对某型液体火箭发动机试验装配中M12×1.25、M14×1.5和 M16×1.5,材质为 1Cr18Ni9Ti的球头-锥面螺纹连接件进行力矩值统计与分析,得出两种环境下的力矩值变化如图2所示。
由图2可知,按1σ准则剔除力矩测量子样中的离群值后,在非试验和试验环境下,操作者施加的力矩值分布比较均匀,分析结果如表1所示。
2.3 拧紧力矩强度理论计算
为验证统计力矩区间的准确性,对球头-锥面螺纹连接件进行拧紧力矩理论计算,确定造成连接件不可逆损伤的拧紧力矩上限值[4,5]。以 M12 ×1.25,材质为1Cr18Ni9Ti的螺纹连接件为例,计算过程如下:

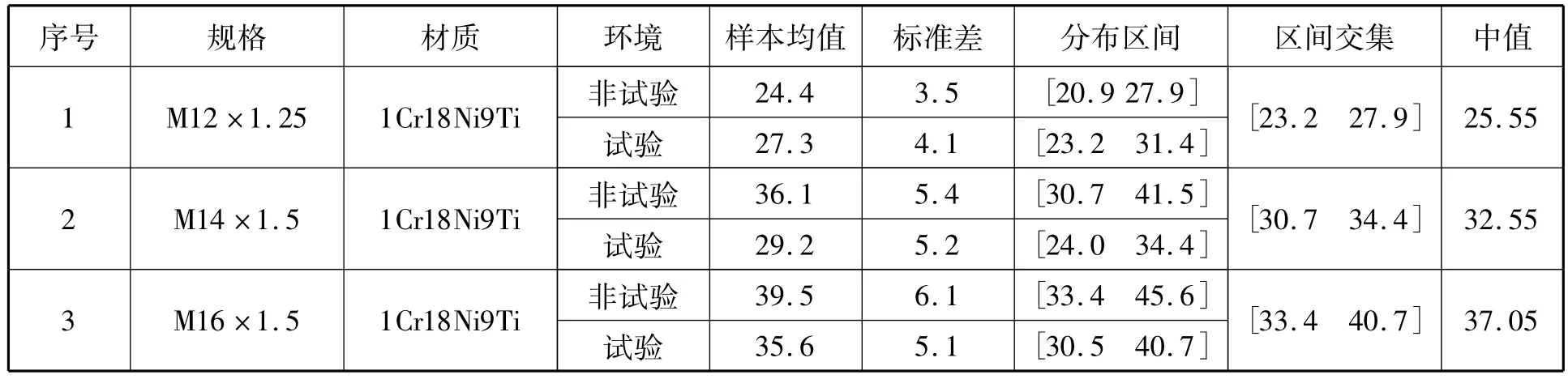
表1 力矩样本分析Tab.1 Analysis of torque samples (N·m)
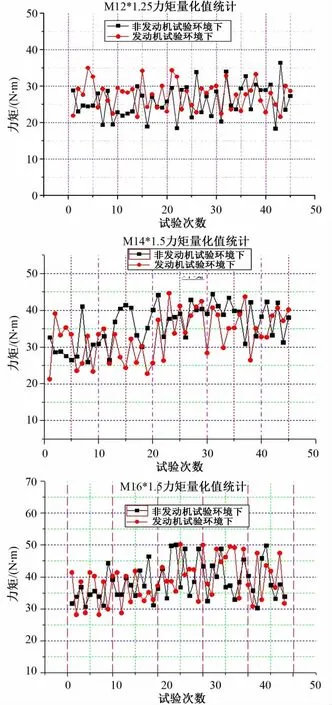
图2 试验/非试验环境力矩值变化曲线ig.2 Torque value curve of test and non-test environment
2.3.1 最大轴向载荷力求解
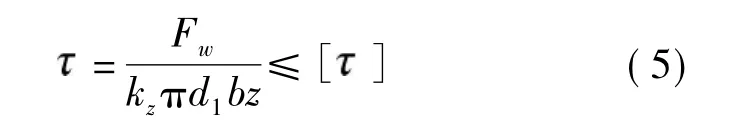
式中:——螺纹切向力;Fw——最大轴向载荷力;kz——载荷不均匀系数;d1——外螺纹小径;b——螺纹牙根部宽度,普通螺纹的螺纹牙根部宽度为0.87P(螺距);z——螺纹牙的个数 (取z=8);[ ]——螺纹许用切向力。
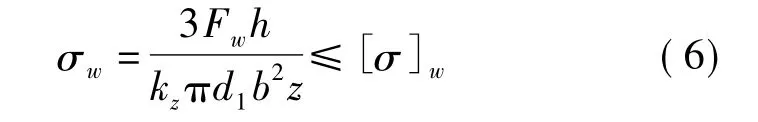
式中:σw——材料的屈服强度;h——螺牙高度,h=0.5413P;[σ]w——材料的屈服极限。当d/P<9时,kz=5P/d,当d/P>9时,kz=0.56。
针对M12×1.25的细牙螺纹d1=10.647mm,P=1.25mm;则h=0.5413P=0.677;
d/P=12/1.25=9.6>9,故取kz=0.56。
b=0.87P=1.0875mm

取σs=340MPa(σs为最大屈服极限,屈服点按4.8 级计算),nτ=1.25,则
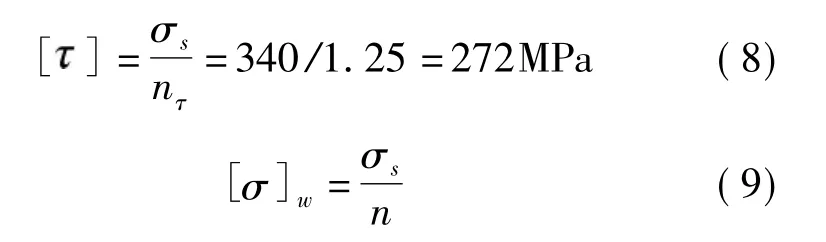
取n=1.5,则
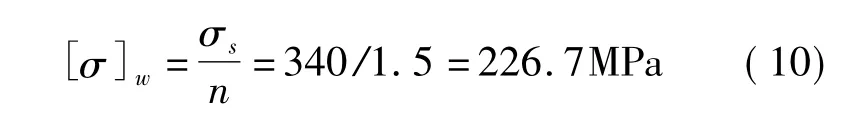
将上述计算结果代入式(5)可得Fw满足
将上述计算结果代入式(6)可得Fw满足
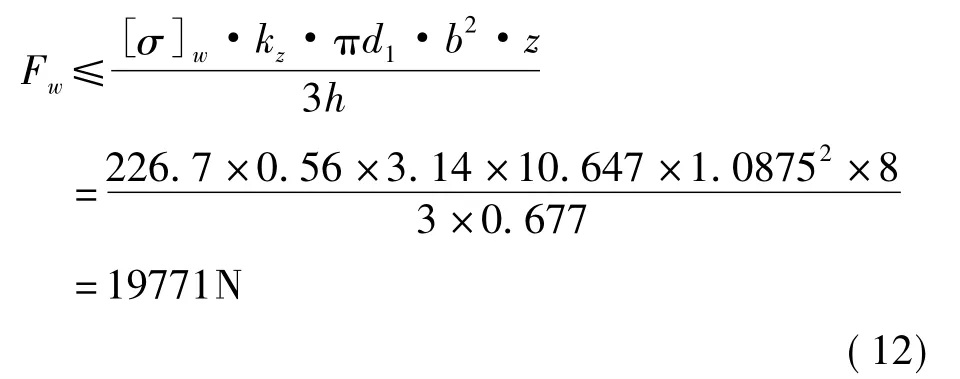
联立式(11)、(12)得,对于规格为M12×1.25、材质为1Cr18Ni9Ti,强度为4.8级的球头-锥面型螺纹连接件,最大轴向载荷力为19771N。
2.3.2 极限拧紧力矩求解

式中:T——拧紧力矩,N·m;K——拧紧力矩系数(一般加工表面K=0.2);Fo——螺纹受到的轴向力;d——螺纹公称直径(d=12mm)。取Fo=Fw,则极限拧紧力矩为
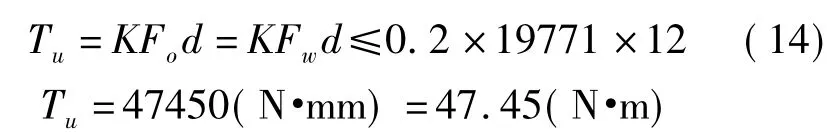
同理,M14×1.5,4.8级的球头-锥面螺纹连接件的极限拧紧力矩为77.3N·m;M16×1.5,4.8级的螺纹连接件的极限拧紧力矩为102.3N·m。结合表1可知,实际统计分析的力矩值均未超过对应规格的极限力矩,故操作者通常施加的拧紧力矩不会对连接件造成不可逆损伤,表1中所分析的力矩值可作为工艺装配的参考实施力矩。
3 力矩量化控制方法和流程
根据某型液体火箭发动机试验台现场情况,某些装配点的空间位置适合力矩扳手直接量化,而某些装配点的安装空间非常狭小,为直接实施力矩量化带来了困难[6],如图3所示。根据试验台装配点的空间位置属性确定了三种力矩量化的方法,如表2所示。

图3 试验现场空间特点Fig.3 Test-site space

表2 装配点属性Tab.2 Attributes of assembly points
3.1 直接法
(1)将装配点球头垂直对正锥面接管嘴;
(2)使用数显力矩扳手施加预紧力矩,预紧力矩值5N·m;
(3)参照表1区间中值设置数显力矩扳手力矩报警值;
(4)使用力矩扳手直接施加力矩,直至出现报警,停止操作。
3.2 间接法
(1)结合装配点空间位置,设计、制作和选用特定异型力矩扳手转接件。
(2)转换拧紧力矩值
根据施加的力矩值和转接件的有效长度,换算数显力矩扳手表牌显示值,换算方式为
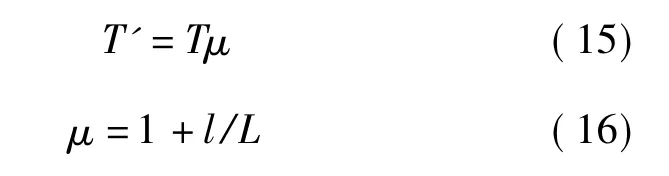
式中:T'——数显力矩扳手显示值,N·m;μ——换算系数,无量纲;l——转接件有效长度,mm;L——数显力矩扳手有效长度,mm。
(3)将装配点球头垂直对正锥面接管嘴;
(4)根据装配点的螺纹规格、预紧力矩值(5 N·m)和转接系数,设置数显力矩扳手预紧力矩报警值,并施加预紧力矩;
(5)设置力矩扳手的力矩报警值;
(6)使用力矩扳手+转接件施加力矩,直至出现报警,停止操作。
3.3 转角法
3.3.1 拧紧力矩与螺母转角关系的理论分析
在螺母最佳装配状态下,对螺母施加拧紧力矩,轴向载荷力与螺母的转角关系[7]为
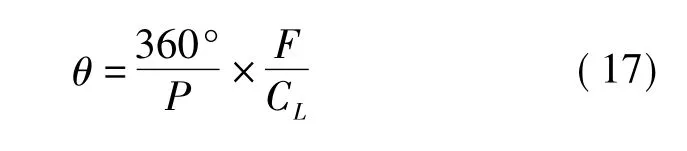
式中:θ——螺母转动角度,(°);F——轴向载荷力,(N);P——螺距,(mm);CL——螺纹的刚度,(N/mm)。
实际拧紧一个螺母时,对同一个球头-锥面螺纹螺母连接件来讲,螺距和螺母刚度都为常量。当螺母与被连接件紧贴时,轴向载荷力与转角约呈线性关系[5],如图4中BC段所示。由式(13)可知,螺纹连接件拧紧力矩与轴向载荷力呈线性关系,因此拧紧力矩与螺母转角也应呈线性关系。
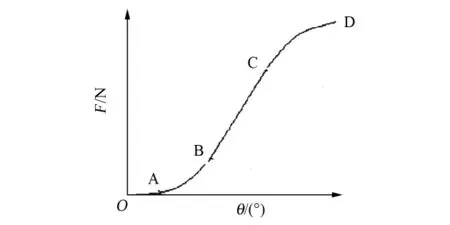
图4 轴向载荷力与螺母转角的关系Fig.4 Relationship of axial-force and corner
3.3.2 拧紧力矩与螺母转角关系试验
在非发动机试验环境下,对M12×1.25、M14×1.5和M16×1.5三种规格的球头-锥面螺纹螺母连接件分别进行拧紧力矩与螺母转角关系的试验。每种规格选取4件进行测试,共进行4次试验,取统计平均值得到拧紧力矩与螺母转角的对应关系如图5所示。
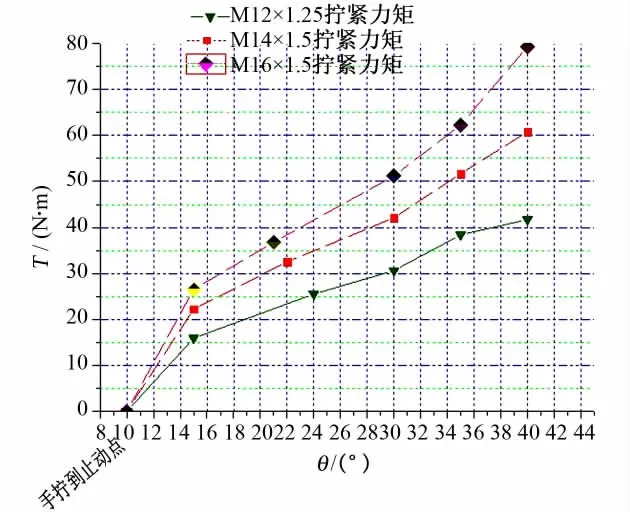
图5 拧紧力矩与螺母转角关系Fig.5 Relationship of torque and corner
由图5可知,在考虑各种物理因素的影响下,拧紧力矩和螺母转角近似呈线性关系。结合表1得M12×1.25的螺母在转角24°时,拧紧力矩约为25.3N·m;M14 ×1.5的螺母在转角22°时,拧紧力矩约为32.7N·m;M16 ×1.5的螺母在转角21°时,拧紧力矩约为37.2N·m,均在各规格球头-锥面螺纹连接件拧紧力矩区间交集之内,并且靠近区间中值。由此可以认为,对于三种规格的C类测点,采用对应角度的转角法可实现力矩量化的精确控制。
3.3.3 转角法力矩量化控制操作方法
(1)将装配点的球头垂直对正发动机锥面接管嘴;
(2)将螺帽手动拧到止动点,使用记号笔在螺帽上沿轴向作一记号,作为角度测量的起始点;
(3)对每种规格的球头-锥面连接件使用角度仪测量出起始记号线沿顺时针方向的相应角度,并用记号笔在接管嘴和螺帽上标注停止线。
(4)使用铜质扳手固定发动机接管嘴,使用另一铜质扳手沿拧紧方向转动螺帽至接管嘴标注停止线,停止拧紧,取下工具。
4 实施效果
将本文提出的力矩量化控制方法和各规格参考中值力矩在多次某型氢氧发动机试验测点装配中进行了应用和试验考核。应用结果表明:所有球头-锥面螺纹连接处漏率均满足试验要求。部分测点气密性检查数据及试验后状态检查情况如表3所示,验证了该方法的有效性。

表3 ××530D-1/××-2D次试车部分测点气密性及状态检查结果Tab.3 Air-tightness and status results for partial points in ××530D-1/××-2D test
5 结束语
通过对液体火箭发动机试验台球头-锥面螺纹连接件的装配过程进行力矩量化控制研究,确定了液体火箭发动机试验台螺纹拧紧力矩值区间;通过拧紧力矩强度理论计算,验证了力矩值区间的合理性;结合试验台螺纹空间位置的具体特点,总结出了试验系统不同部位装配点的力矩量化控制方法和工艺流程。本文所述的力矩量化值和工艺方法在某型氢氧发动机试验中的得到了实际应用,改进了以往螺纹装配靠操作者经验保证的不足,提高了工艺装配的可靠性和有效性,实现了试验系统上螺纹装配的全面量化操作。
