基于风致振动机理的压电发电机实验及仿真研究
2019-08-31陆油松张大有赵悄然
陆油松 张大有 赵悄然 隋 丽
(1.北京理工大学,北京100081;2.北京航天计量测试技术研究所,北京100076)
1 引言
随着低功耗微机电系统的发展,涌现出许多微型发电装置为低功耗设备供电,其中压电发电机就是典型的代表。压电材料和压电俘能器具有广泛的应用前景和巨大的开发潜力,但是基于现有技术的局限性,压电发电机仅适用于耗电量较小的小功率设备。为研究影响压电发电机发电性能的参数,提高压电发电机的能量输出特性,研究人员对压电发电机的俘能机理、结构优化等方面进行了理论、仿真和实验等方面的研究。
Chen,Wang 和 Chien(2006)[2]推导了双压电晶片在正弦激励下的发电性能,同时设计实验验证了理论研究的正确性,其理论推导得到的最大电压值与实验得到的最大电压值较为接近。单小彪,袁江波,谢涛等(2010)[1]和王浩金,邬丹燕,肖金等(2011)[3]等对单晶压电梁进行了数学建模和仿真。Kundu和 Nemade(2016)[4]对双晶压电梁进行了数学建模和仿真。阚君武,唐可洪,王淑云等(2008)[5]分别对单晶压电梁和双晶压电梁进行了数学建模和仿真。Stanton,Erturk,Mann等(2010)[6,7]研究了压电材料非线性对压电俘能器动态力学的影响。Doar,Eacute 和 Michelin(2011)[8]研究了风致振动压电俘能器的线性稳定问题和转换效率。Zhao,Liu,Wang 等(2017)[9]研究了低频扰动条件下压电俘能器的能量收集性能。Yee,Radeef,Chao等(2017)[10]研究了俘能器结构动力学对其俘能效果的影响。Abdelmoula和 Abdelkefi(2016)[11]研究了阻抗对基于驰振的能量收集系统俘能效果的影响。Hong,Sui,Zhang 等(2018)[12]对复合压电悬臂梁中性面对其俘能效果的影响进行了研究。
针对微机电系统及微型压电发电机的发展现状,本文对一种基于风致振动机理的柔性压电悬臂梁进行了实验及仿真研究。致力于探究柔性悬臂梁的颤振机理及其在不同流速环境中的电压输出特性,同时研究在二阶颤振条件下单个压电悬臂梁给电容充电的充电性能,为建立风致压电发电机模型提供仿真依据。
2 压电柔性悬臂梁颤振机理仿真
压电柔性悬臂梁是压电发电机的能量转换元件,其在风场中的振动是一个复杂的受力过程。为提高压电发电机的输出性能,需对压电柔性梁与流场的流固耦合模型进行研究,悬臂梁与安装夹具的流固耦合示意图如图1所示。
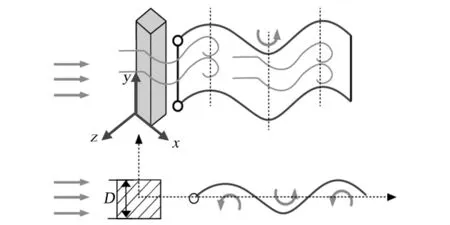
图1 柔性梁在风场中的振动示意图Fig.1 Vibration diagram of flexible beam in wind field
2.1 柔性梁在风场中的颤振分析
为探究压电柔性悬臂梁在流场中的颤振机理,本文采用COMSOL软件对压电悬臂梁进行流固耦合仿真。压电悬臂梁模型由一层压电材料(PVDF)和一层304不锈钢基底材料构成,其几何尺寸和材料参数如表1所示,有限元模型如图2所示,图中方块为模拟压电悬臂梁的夹具,后方的黑色直线是压电悬臂梁的侧视效果。
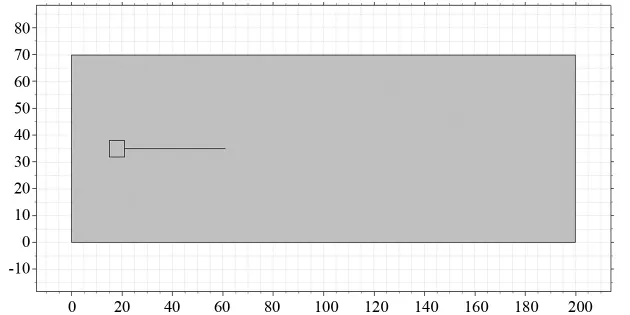
图2 流固耦合仿真模型Fig.2 Fluid-Structure-Interaction simulation model
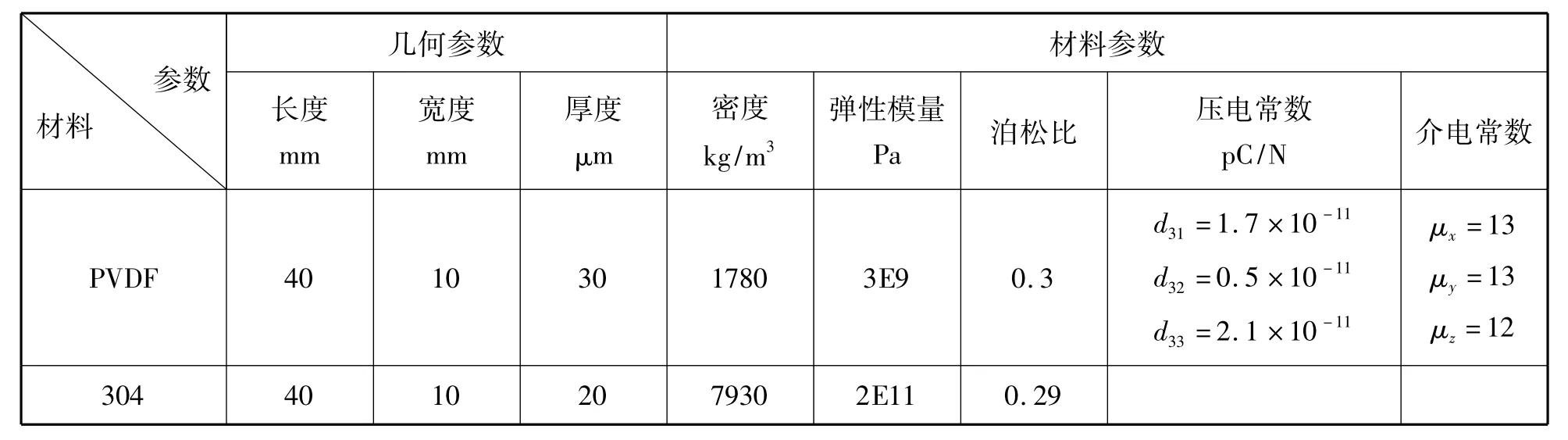
表1 压电悬臂梁的模型参数Tab.1 Model parameters of piezoelectric cantilever
由于有限元算法的要求,风场加载是一个带有一定斜率的阶跃加载过程,即将目标风速乘一个阶跃函数,函数在不同时间所对应的的值为与目标风速相乘的系数。阶跃函数曲线如图3所示,调节阶跃函数的斜率可以改变加载时间,这样避免了直接加载目标风速造成的不收敛。
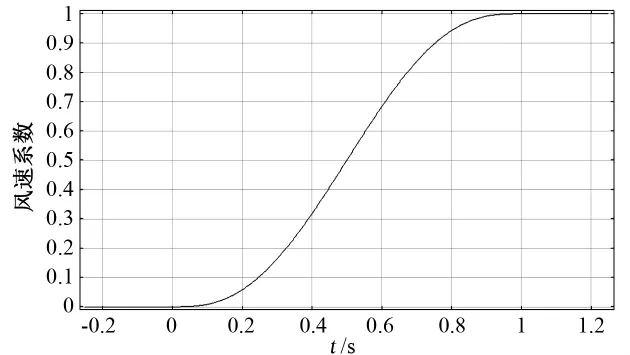
图3 阶跃函数曲线Fig.3 Step function curve
柔性悬臂梁在风场中的状态由静止到规律振动的风速叫做临界风速,临界风速是压电悬臂梁振动系统的重要参数。当风速大于临界风速时,柔性梁的自激振荡可以维持;风速低于临界风速时,振动则慢慢衰减,逐渐趋于静止。在设计过程中,应根据实际风速环境设计压电悬臂梁的结构参数。图4是表1所列压电悬臂梁在风速为20m/s的风场中的自由端位移特性曲线。从图中可以看出,当风速较低时,柔性梁做低频振动,振幅较小;当风速高于临界风速后,柔性梁做大幅值周期振动。由图4可知,当时间t>0.6s后,压电悬臂梁发生颤振,对应于阶跃函数曲线可知压电柔性悬臂梁的颤振临界速度约为15m/s。
2.2 柔性梁在风场中发生颤振时的力学环境
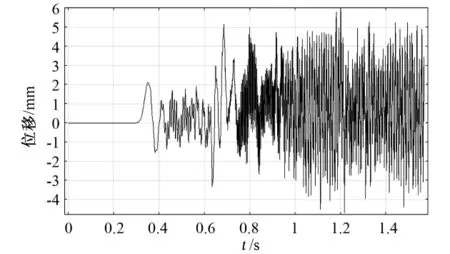
图4 压电悬臂梁振动时自由端位移特性曲线Fig.4 Displacement distributions of trailing edge when flutter occurs
压电柔性悬臂梁在风场中的振动是一个复杂的受力过程,从图5中可以看出,由钝体阻挡产生的涡街沿着柔性梁长度方向交替分布,导致柔性梁上压强较大的点不是单一的,造成柔性梁多个受力点同时作用,这些交变力使压电悬臂梁往复振动。
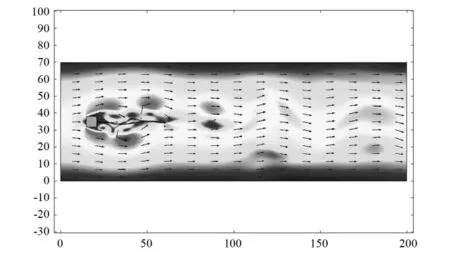
图5 柔性梁周围的涡街分布Fig.5 Vortex distribution around pizoelectric beam
3 压电发电机输出性能实验
通过对压电悬臂梁的流固耦合分析,对其在风场中的振动特性有了初步了解。为验证压电发电机在不同风速环境下的发电性能,本文将对单层压电悬臂梁的输出特性及充电性能进行测试。悬臂梁的尺寸为:长50mm,宽10mm,PVDF厚度0.03mm,基底厚度0.02mm。
3.1 实验设计
为检测压电发电机在风场中的发电性能,按照如图6所示的实验方案搭建了测试平台,用于模拟柔性梁和流场的流固耦合模型。本文采用鼓风机进行风速加载,整个测试平台由鼓风机、风速仪、直流稳压电源、示波器等组成。

图6 总体实验方案Fig.6 Schematic of experimental scheme
测试平台实物图如图7所示。鼓风机的型号为“HAOBANG HB9026”、额定电压为220V、风速范围为(0~50)m/s,可以手动控制风速大小,也可以将风速固定在某一恒定值。风场范围可通过改变套在鼓风机口的套筒直径进行调节,套筒直径越小能够达到的风速则越高。稳压源的作用是给风速仪提供稳定的直流电压,型号为“XD1722”、电压范围为(0~30)V。

图7 鼓风机加载实验系统Fig.7 Diagram of Experimental setup
风速由型号为“KIMO CP 200”的风速仪测量,它由皮托管和变送器两部分组成。法国KIMO公司的TPL-03-300型皮托管外径为3mm,总压孔直径仅为1mm,适合应用于微小型器件内的流体速度测量。变送器使用法国KIMO公司的CP-202型号,风速测量范围为(3~100)m/s;分辨率为0.1m/s。实验时,将风速仪的风速输入口放在鼓风机吹风口处,当风速大于悬臂梁的临界风速时,悬臂梁发生大振幅的颤振,压电材料将振动能转换为电能,通过引出电极连接到示波器,来观测压电悬臂梁的输出电压及波形。
3.2 压电发电机开路电压实验结果
压电悬臂梁在低风速下的振动情况及输出电压信号如图8所示。由高速摄影机拍摄到的图像可知,在达到临界风速前,压电悬臂梁在风场中只有很小幅度的颤动,整体处于稳定状态,输出电压几乎为零。
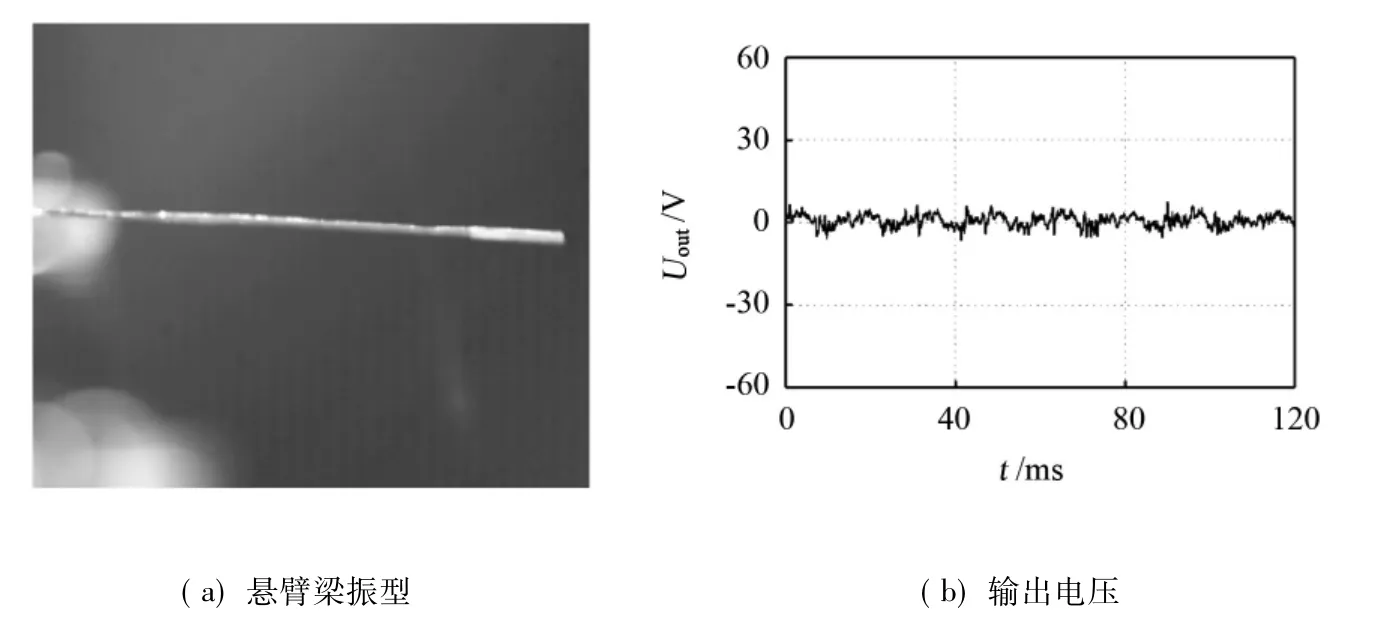
图8 低于临界风速时压电悬臂梁的振动及输出电压Fig.8 Vibration mode(a)and output voltage(b)of piezoelectric cantilever under the conditions of subcritical flutter velocity
当风速持续增加并超过一定值时,压电悬臂梁开始大幅值振动,振型及输出电压如图9所示,对比悬臂梁振动阵型可知,悬臂梁的振动姿态属于二阶振动。悬臂梁起振时的风速即为颤振风速或临界风速。压电悬臂梁的输出波形是规律的近似正弦波的交流信号,且峰值较高,图中所示为20V。
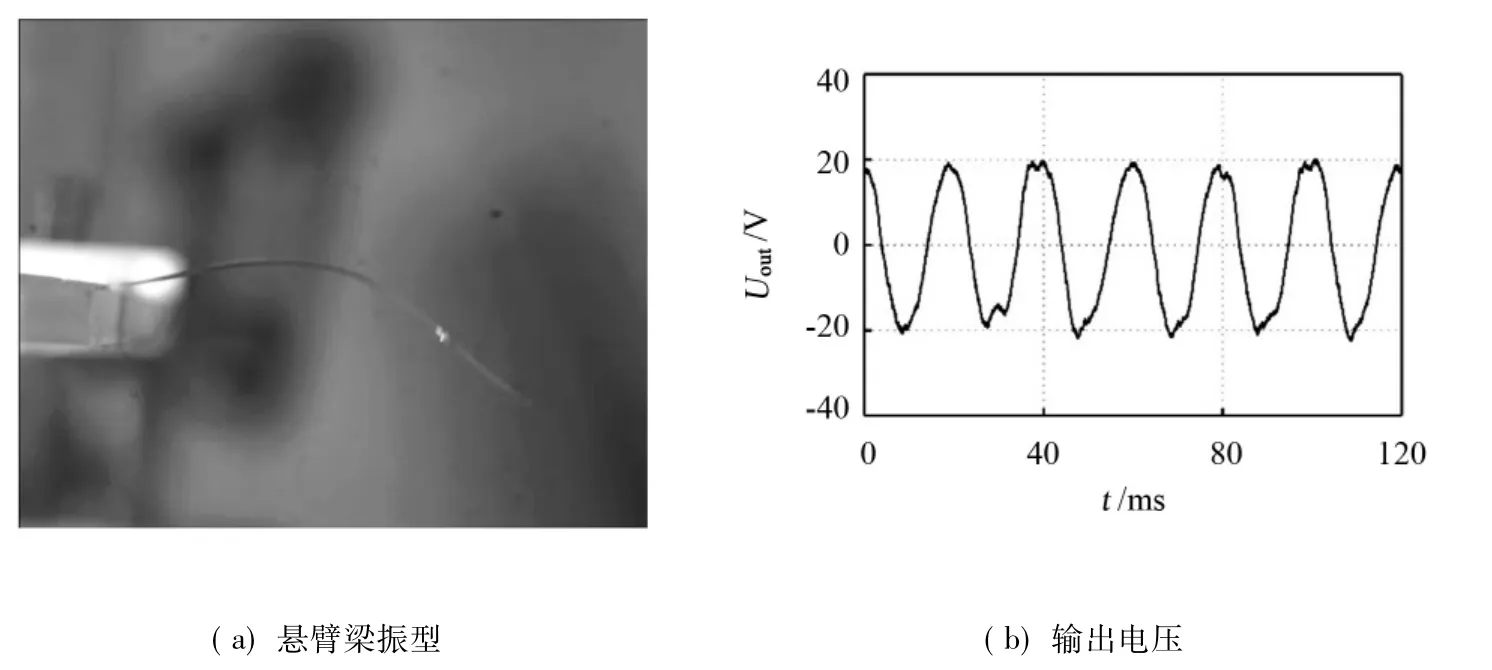
图9 达到临界风速后压电悬臂梁的振动及输出电压Fig.9 Vibration mode(a)and output voltage(b)of piezoelectric cantilever under the conditions of supercritical flutter velocity
令风速从低到高增长,记录压电悬臂梁在不同风速下的输出电压值,绘制风速-电压曲线如图10所示。由图可知,当风速由0增加到15.2m/s(临界风速)的过程中压电悬臂梁的输出几乎为零,当风速超过15.2m/s时输出电压突然增加,呈阶跃变化。这是因为在此风速下,系统的净阻尼变为负值,系统由稳定变为非稳定状态,产生大幅自激振动。随着风速继续增大,振动系统能够从外界汲取更多的能量用于维持自身振动,压电悬臂梁仍保持着较高的电压输出且保持上升的趋势。当风速增加到一定程度时,柔性梁的规律振动将被破坏,振型随之变得混乱,同时输出电压的波形变为锯齿状。虽然此时输出电压的幅值依然较大,甚至在某些位置出现很大的峰值,但是这种振动情况要避免。一方面因为这种振动模态下压电悬臂梁受到的力不规律,易造成柔性梁损坏;另一方面是因为过于混乱的波形会给后续的电源管理电路的器件选择和最终电能存储造成困难。
3.3 压电发电机为电容充电实验结果
通过上述实验可知,压电悬臂梁在一定的风速范围内能够有规律地振动,且输出高幅值的交流电压。如图9(b)所示,压电悬臂梁由于振动所产生的电压是交流信号,不能直接给引信电路供电,需要将信号进行整流变换为直流电。另一方面,尽管压电悬臂梁的输出电压相对较高,但电流极小,能量微弱,因此在使用时,需将压电悬臂梁输出的电能转化为直流信号后存储于储能电容中,再在控制信号的激发下完成供电,流程如图11所示。
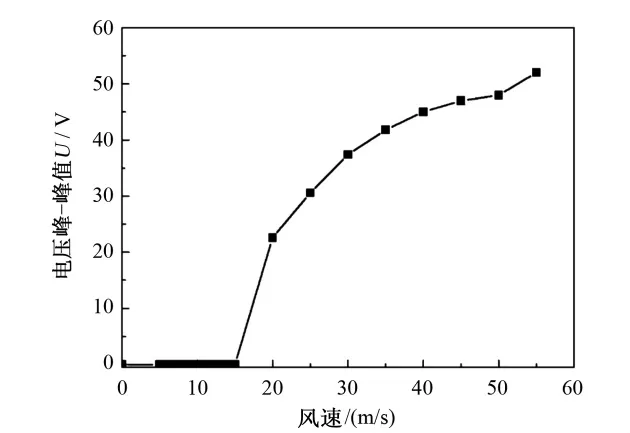
图10 电压-风速曲线Fig.10 Voltage-Velocity curve
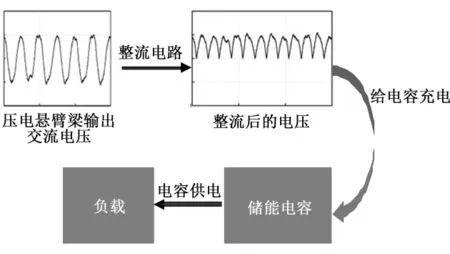
图11 储能流程图Fig.11 Energy storage diagram
上述流程由电源管理电路来完成,本文选择结构最简单的标准电源管理电路,如图12所示。
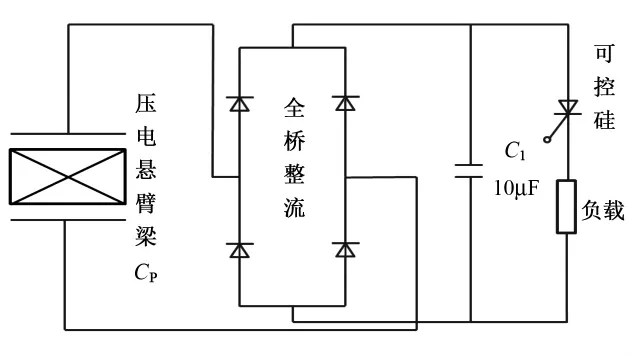
图12 标准电源管理电路原理图Fig.12 A standard energy harvesting circuit
在图12所示的电路中,压电悬臂梁的输出被视作电压源,由于其内阻很大,可将它等效为一个电容CP。压电悬臂梁产生的交流电压经过全桥整流,输出脉动直流电压,直流电压再向能量存储电容C1不断充电。当可控硅的控制极为低电平时,负载开路,压电悬臂梁产生的电荷被完全储存在电容中,不会产生泄露,充电电路的时间常数相当于充电电容C1乘上压电悬臂梁的输出阻抗。
电容的充电曲线如图13所示。与理想的充电曲线相似,充电曲线能够反映出压电发电机的输出功率稳定,从另一个侧面反映出悬臂梁的振动平稳。5s后,电容充电为8V,10s后,电容充电为22V。
由电容能量公式:Pt=1/2CV2,计算电容的充电功率,可以知道5s时充电功率为0.64mW,10s时充电功率为2.42mW,电容充电的功率能够满足低功耗设备的供电要求。
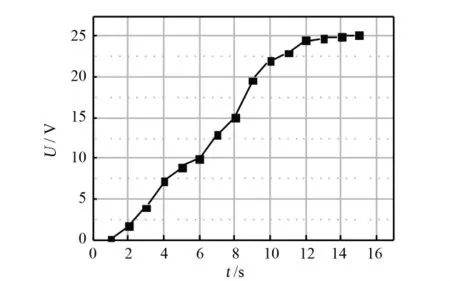
图13 单压电层悬臂梁给电容的充电曲线Fig.13 Charging curve with one singlepiezoelectric cantilever
4 结束语
本文通过对压电柔性悬臂梁的流固耦合仿真以及发电性能的实验探究,得出:
(1)柔性悬臂梁在流场中振动的原因是由悬臂上下面的交替压强差引起的。当流速高于某一速度值时,柔性体会发生大幅度的振动,即颤振,该速度即为颤振临界速度。
(2)当流速低于颤振临界速度时,压电悬臂梁的输出几乎为零。当流速达到颤振临界速度时,压电悬臂梁输出电压为类正弦曲线交流电,且峰-峰值较高。当风速增加到一定程度时,悬臂梁的规律振动将被破坏,振型随之变得混乱,同时输出电压的波形变为锯齿状。
(3)单个压电悬臂梁为10μF电容充电5s可达8V,充电功率为0.64mW,充电10s可达22V,充电功率为2.42mW。微型压电发电机为低功耗微机电系统设备供电成为可能。
