铸件中显微孔洞特征及其对疲劳寿命影响的研究进展
2019-08-30姜文姚卫星王英玉
姜文,姚卫星,2,王英玉
(1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016)(2.南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
0 引 言
以镍基高温合金和高质量铸造铝合金为代表的高端铸造合金是航空发动机、燃气轮机以及汽车发动机制造的基础,在航空航天、汽车等领域应用广泛[1-2],但是在服役过程中往往承受交变载荷和高温作用,产生循环塑性变形累积而导致疲劳失效[3]。疲劳失效裂纹往往萌生于孔洞处,并在孔洞处有较大的裂纹扩展速率[4],使得孔洞缺陷成为制约其疲劳寿命的关键因素之一。随着铸造技术的提高,宏观孔洞已经能够基本消除,但是依旧无法避免枝晶间显微孔洞的产生[5-6]。这些显微孔洞尺寸范围通常在几微米至几百微米之间,形状较为复杂,它们的存在破坏了基体的连续性,在变形过程中造成应力集中,成为疲劳失效的裂纹源头,严重降低了结构疲劳寿命[7]。
近年来,国内外也有一些关于铸件中显微孔洞方面的综述。例如,侯延辉等[8]综述了铸造气孔物理模型的研究进展;张杰等[9]综述了铸件中孔洞缺陷对裂纹萌生和裂纹扩展的影响;康茂东等[10]综述了铸件中显微疏松缺陷的表征方法及其对疲劳性能的影响;P.D.Lee等[11]综述了铸造铝合金中显微孔洞物理模型;A.R.Adamane等[12]综述了合金液注入参数对显微孔洞形成及铸件拉伸性能的影响。目前相关综述主要集中在显微孔洞形成模型和试验表征,关于微孔洞对疲劳性能影响的综述较少,尤其缺乏不同显微孔洞特征参数(例如孔洞尺寸、孔洞外貌、空间分布、体积分数等)对疲劳寿命定量影响的综述。
本文主要以镍基高温合金和铸造铝合金为例综述铸件中显微孔洞的类型及特征,显微孔洞特征参数的分布规律,显微孔洞最大尺寸预测方法,以及考虑不同显微孔洞特征的铸件疲劳寿命预测方法,并对显微孔洞特征对疲劳寿命影响的研究进行展望。
1 显微孔洞的类型及特征
显微孔洞类型如图1所示,显微孔洞按照其形成时间的先后可以归结于三种:合金凝固过程中产生的铸态微孔;固溶热处理过程中产生的固溶微孔;以及服役过程中产生的蠕变微孔[13-15]。
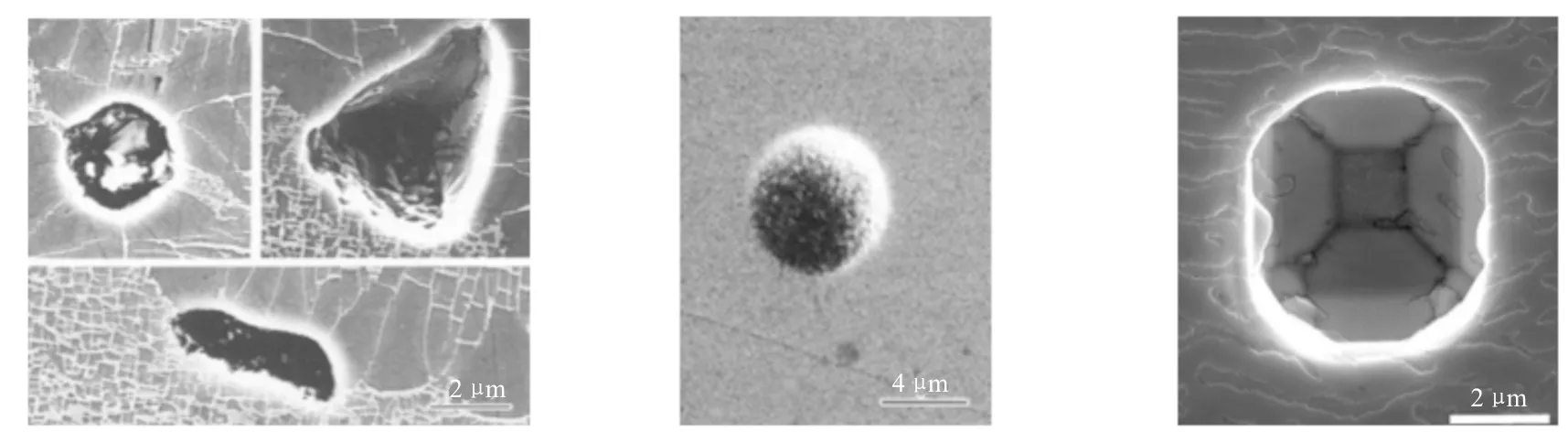
(a)铸态微孔 (b)固溶微孔 (c)蠕变微孔
图1 显微孔洞类型
Fig.1 Types of microporosities
1.1 铸态微孔
铸态微孔按照形成机理的不同可以分为缩松、缩孔和气孔三类[16-18]。缩松的形成原因是元素偏析造成合金液局部凝固成密闭空间,空间内合金液收缩后得不到补充。缩孔的形成原因是一次枝晶的生长阻碍了合金液向枝晶间流动,枝晶间合金液凝固后得不到补充。气孔又可以分为析出性气孔、倾入性气孔和反应性气孔,形成的原因分别是合金液中溶解的气体析出,型膜高温下产生气体倾入到合金液中,合金液中析氢等反应产生气体。
铸态微孔的平均直径在3 μm左右,75%的铸态微孔的尺寸小于4 μm,只有个别铸态微孔直径超过10 μm[14]。不同类型的铸态微孔外貌和空间分布差异较大,缩松一般产生于沿重力方向的枝晶间,以长条状疏松通道出现;缩孔主要产生于枝晶间两相共晶组织附近,主要呈现不规则的长条形和三角形[17];析出性气孔在气体含量较低时为多角形状,在气体含量较高时为近球形,倾入性气孔外形一般为梨形,梨尖指向气体倾入方向[16,18]。铸态微孔的内壁粗糙不平,数量约占所有显微孔洞的80%,由于铸造工艺的提高,合金中气体含量控制的很低,铸态微孔绝大多数是缩松和缩孔缺陷[19]。
1.2 固溶微孔
为了使铸材内部组织均匀,获得良好的力学性能,必须对铸材进行固溶热处理,这一过程中会形成固溶微孔。固溶微孔的形成原因目前主要认为是基于Kirkendall效应不平衡扩散产生的空穴聚集[14]。固溶微孔的直径主要在5~30 μm之间,平均直径在8 μm左右,外貌多为球形或者近球形,内壁相对平整光滑[13-14]。空间分布上远离自由表面固溶微孔的体积分数降低,固溶微孔的数量约占所有显微孔洞的10%[5]。
1.3 蠕变微孔
蠕变微孔的形成原因是材料在服役过程中承受蠕变载荷产生大应变,蠕变应力、蠕变时间以及蠕变温度均会影响蠕变微孔的尺寸和数量[20]。蠕变微孔的直径主要在2.5~30 μm之间,平均直径在10 μm左右。在蠕变时间较短时蠕变微孔的外貌为近球形,随着蠕变时间增加蠕变微孔的外貌逐渐向立方体转化,蠕变微孔的数量约占显微孔洞数量的10%[13]。
2 显微孔洞特征参数分布规律
很多学者通过小尺寸试验件,采用定量金相法[22]、X射线断层扫描[23-26]以及同步辐射光源[15-17,27]研究了铸件中显微孔洞的特征,本节通过文献中的试验数据,总结出铸造合金中显微孔洞特征参数的分布规律。
2.1 尺寸特征分布规律
显微孔洞的尺寸d指与孔洞面积相等圆或体积相等球的直径,目前普遍认为铸造合金中显微孔洞尺寸服从对数正态分布[28-31],对文献[13]中四种标准热处理后镍基单晶高温合金显微孔洞尺寸分布试验数据进行对数正态分布拟合,如图2所示,其中p为概率密度,μ为均值,σ为标准差,R2为拟合相关系数。
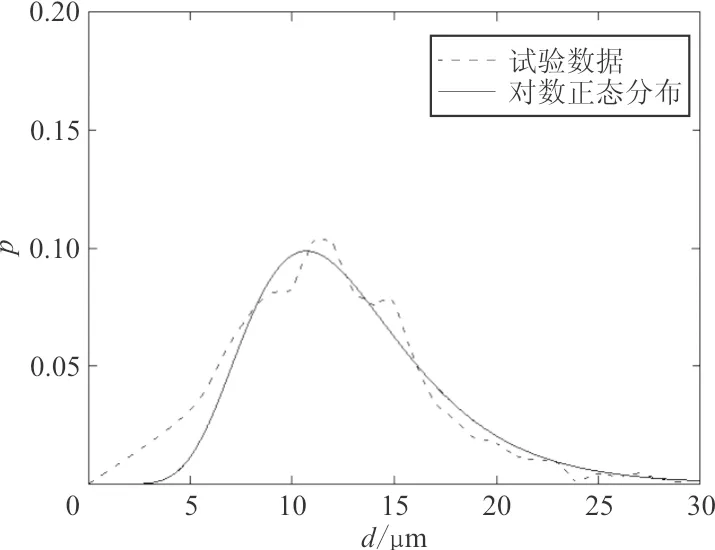
(a)CMSX-10合金(μ=2.489 5,σ=0.352 6,R2=0.97)
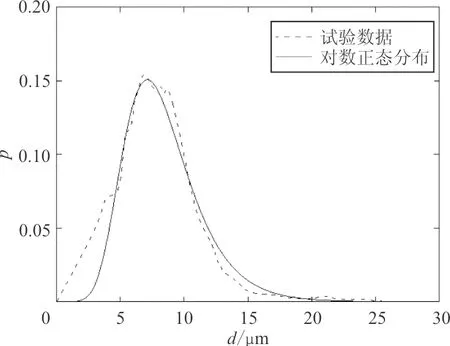
(b)CMSX-4合金(μ=2.071 1,σ=0.344 9,R2=0.98)
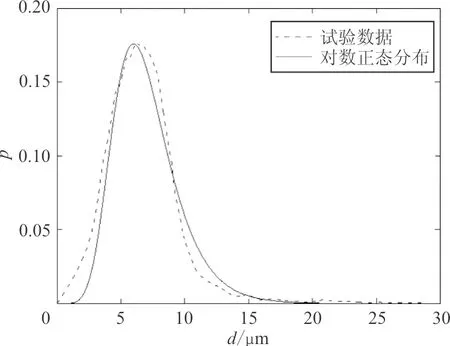
(c)CMSX-6合金(μ=1.896 7,σ=0.347 9,R2=0.98)
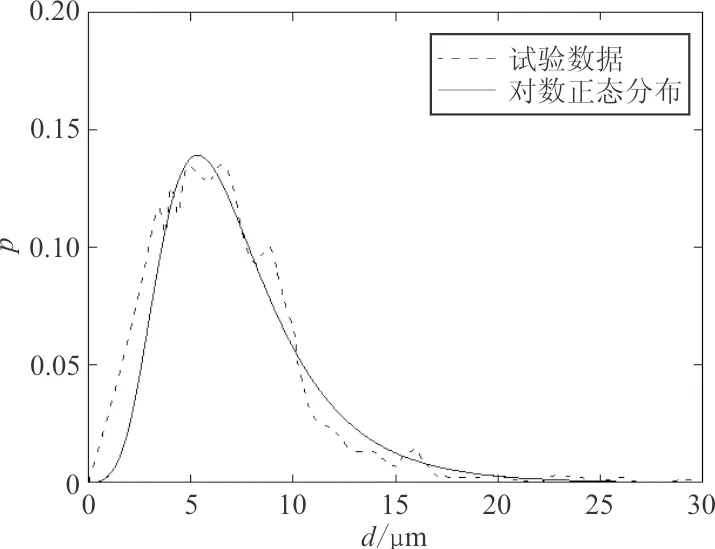
(d)SRR99合金(μ=1.881 9,σ=0.476 4,R2=0.97)图2 显微孔洞尺寸对数正态分布拟合结果Fig.2 The lognormal distribution fitting results of microporosity size
从图2可以看出:拟合曲线相关系数均较高,并且试验曲线在孔洞尺寸较大时与对数正态分布拟合曲线重合度更高,因此对数正态分布可以很好地描述显微孔洞尺寸的分布规律。
2.2 形状特征分布规律
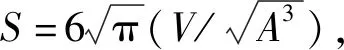

(a)CMSX-10合金对数正态分布拟合结果(μ=0.070 4,σ=0.047 0,R2=0.94)
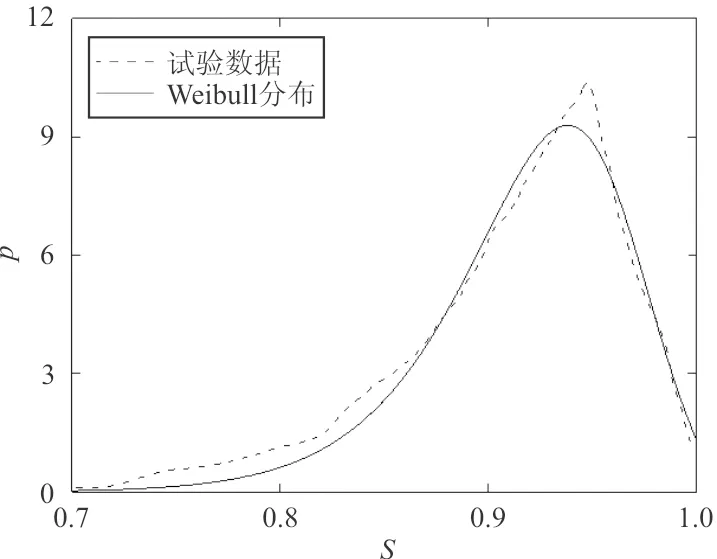
(b)CMSX-10合金Weibull分布拟合结果(λ=4.384,k=23.95,R2=0.99)
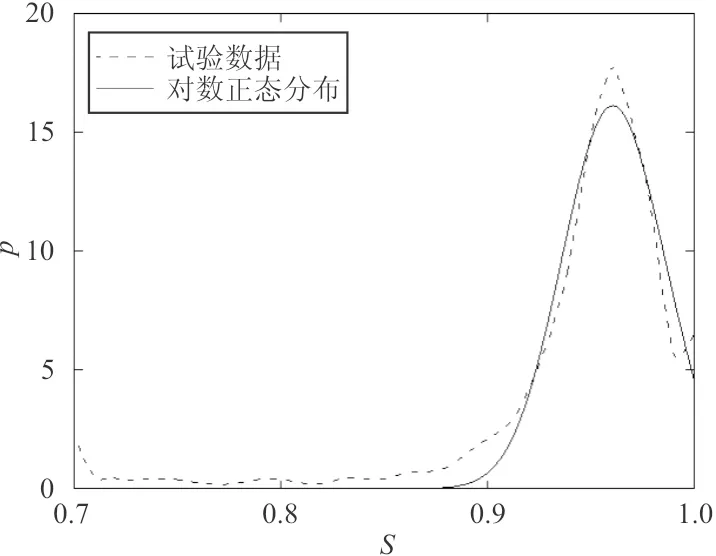
(c)CMSX-4合金对数正态分布拟合结果(μ=0.039 7,σ=0.025 1,R2=0.97)
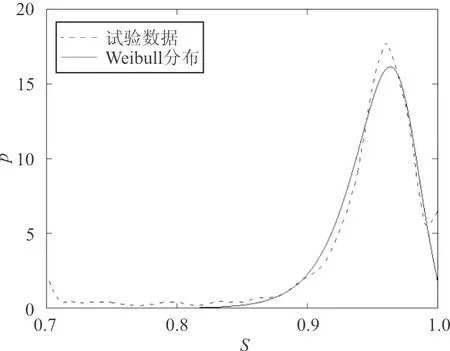
(d)CMSX-4合金Weibull分布拟合结果(λ=4.814,k=43.77,R2=0.97)图3 显微孔洞形状分布拟合结果Fig.3 The fitting results of microporosity shape distribution
2.3 空间特征分布规律
显微孔洞的空间分布可以分为试验件凝固方向分布和厚度方向分布,为方便比较不同尺寸试件中空间分布规律,将孔洞与自由表面的距离除以所在方向上最大试件尺寸得到相对距离。冯广召等[32]研究了不同抽拉速率下DZ125合金凝固方向孔洞面积分数分布规律,如图4所示,结果表明远离浇口的部分孔洞分布相对均匀,但靠近浇口的部分孔洞面积分数明显升高,万谦[26]在铸造铝合金中也发现了同样的规律。喻程等[16]研究了铝合金厚度方向孔洞数量分布规律,如图5所示,发现孔洞数量在试件表面分布有一定波动,远离自由表面孔洞数量缓慢增多,但在靠近试验件中心后孔洞数量迅速降低,作者认为显微孔洞空间特征可以用多项式函数拟合。
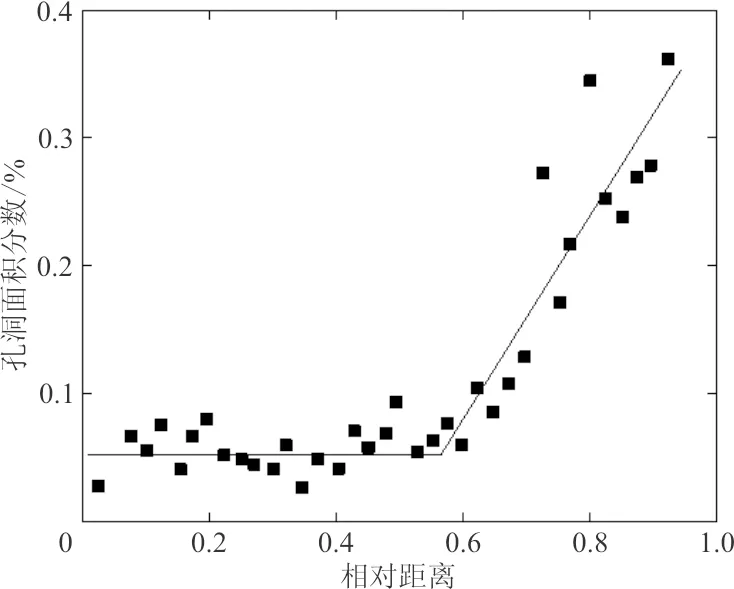
图4 凝固方向孔洞面积分数分布Fig.4 Area fraction distribution of microporosity in the solidification direction

图5 厚度方向孔洞数量分布Fig.5 Quantity distribution of microporosity in the thickness direction
2.4 大尺寸显微孔洞特征参数间的联系
铸件表面或者近表面尺寸较大的孔洞往往对疲劳失效影响很大[33-35],这些尺寸较大的显微孔洞,其尺寸、形状和空间分布之间存在一定的联系。为了比较不同材料、不同尺寸试件中较大尺寸显微孔洞特征参数间的联系,需将孔洞尺寸除以试件中最大孔洞尺寸得到相对尺寸。文献[16,23,36]中相对尺寸大于0.5的显微孔洞圆整度分布数据如图6所示,结果表明试件中尺寸越大的显微孔洞圆整度也较低,大尺寸显微孔洞的尺寸和圆整度近似线性关系。文献[16,17,36]中相对尺寸大于0.5的显微孔洞厚度方向空间分布数据如图7所示,结果表明尺寸较大的显微孔洞倾向于出现在距离自由表面较近的地方,并且最大孔洞往往在距离自由表面相对距离为0.1的地方聚集。因此尺寸特征尤其最大尺寸可以作为显微孔洞的典型特征来评估铸件的疲劳寿命。
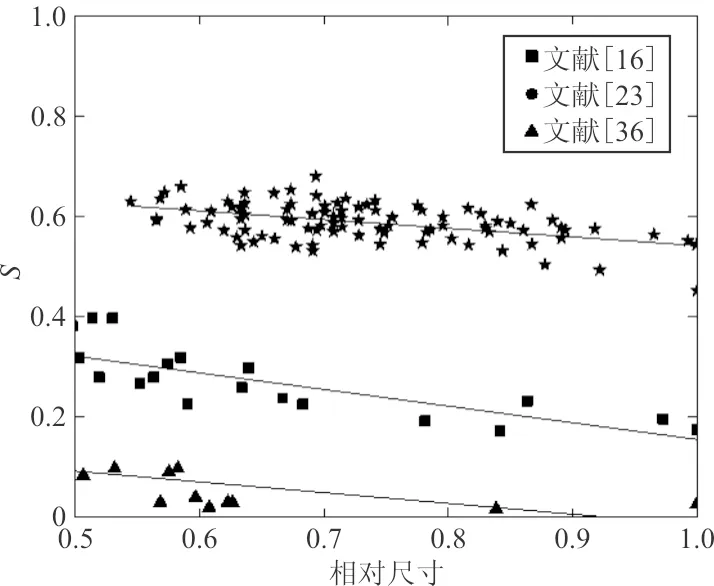
图6 大尺寸孔洞尺寸与形状的分布规律Fig.6 Distribution pattern of large-size microprosity between size and shape
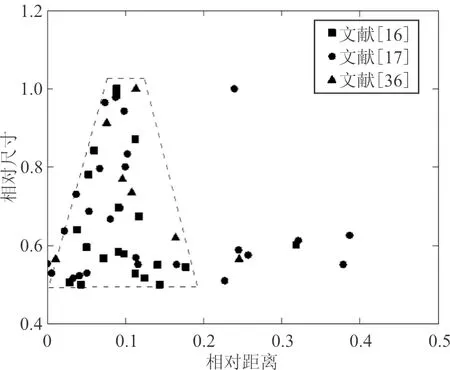
图7 大尺寸孔洞尺寸与空间的分布规律Fig.7 Distribution pattern of large-size microprosity between size and location
3 显微孔洞最大尺寸预测方法
对于大尺寸铸件,采用试验方法观测显微孔洞最大尺寸很难实现,因此常常在大尺寸铸件表面随机选择N个面积很小的区域S0,收集相关统计量,采用统计方法预测大尺寸铸件中显微孔洞的最大尺寸。常用的预测方法有三种:对数正态分布外推法[37],极大值分布法[38-40]和广义Pareto分布法[41-42]。
3.1 对数正态分布外推法
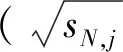
xV=exp{μ+σφ-1(1-(NVV)-1)}
(1)
(a)j=1,…,6 (b)j=1,…,5 (c)j=1,…,7
图8 对数正态分布外推法统计量
Fig.8 Statistics of log-norm distribution extrapolation method
从式(1)可以看出:随着铸件体积的增大,预测值及置信区间均增大,与实际不相符。此外对数正态分布外推法需要统计大量显微孔洞尺寸的信息来获得拟合度较好的对数正态分布函数,这在实际操作中有两大难度[43]:一是尺寸很小的显微孔洞受仪器的限制无法被观测到;二是数量较少的大尺寸显微孔洞对分布函数影响较大,结果稳定性不高。
3.2 极大值分布法
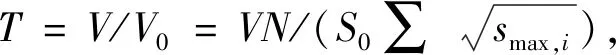
xV=-αln{-ln[(T-1)/T]}+λ
(2)
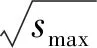
(3)
再将y=-ln{-ln[(T-1)/T]}代入式(3)即可得到xV的估计。
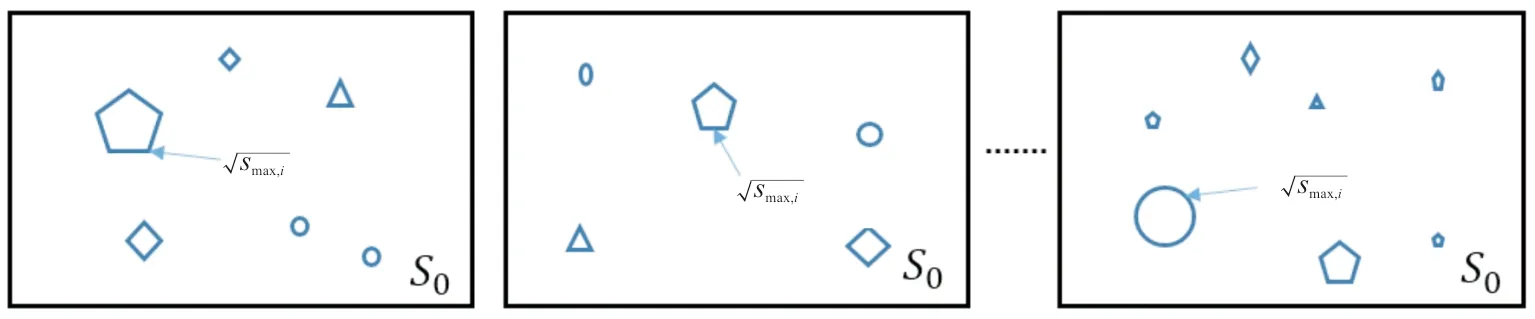
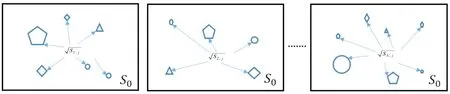
(a)i=1 (b)i=2 (c)i=N
图9 极大值分布法统计量
Fig.9 Statistics of maximum distribution method
从式(2)~式(3)可以看出:随着铸件体积的增大,极大值分布法得到的显微孔洞尺寸极大值预测值及置信区间线性增大,与实际不符。但是极大值分布法只需要统计每一个区域中的尺寸最大值,避免了尺寸较小观察不到的情况,减少了样本统计工作量。
3.3 广义Pareto分布法
广义Pareto分布法假设显微孔洞尺寸服从特定分布,其中大于一定门槛值的显微孔洞尺寸x服从广义Pareto分布,该分布有三个参数,尺寸门槛值μ,尺度参数σ和形状参数ξ,如图10所示。

(a)j=1,…,3 (b)j=1,…,4 (c)j=1,2
图10 广义Pareto法统计量
Fig.10 Statistics of generalized Pareto distribution method
该方法需要统计每一区域中尺寸大于μ的显微孔洞尺寸信息,工程上常采用作图法确定参数,选择不同的门槛值μk,求出超过μk的所有尺寸的平均值xk,做μk-xk散点图如图11所示,找出线性较好的一段进行拟合,线性段开始的值即门槛值μ,对于光学显微镜该值一般为3 μm[41],再由拟合直线的斜率ξ/(1-ξ)和截距σ/(1-ξ)求得参数σ和ξ的估计值。精确度要求较高时可以采用最大似然估计法求解三个参数的估计值,但是计算量较大。
假设体积V的铸件中最大微孔洞尺寸为xV,NV(μ)表示体积V中尺寸超过门槛值μ的微孔洞数量,则可以得到显微孔洞最大尺寸预测值。
(4)
形状参数ξ对广义Pareto分布法的参数估计,尺寸预测值及其置信区间宽度影响很大[42],如果形状参数ξ<0,则最大尺寸预测值存在上限xV=-μ-σ/ξ,更符合实际情况。一般情况下广义Pareto法的预测结果比极大值分布法小,但置信区间比极大值分布法宽。当ξ≈0,广义Pareto分布法和极大值分布法的估计值相近,其他情况下广义Pareto分布法的估计结果优于极大值分布法[45]。但是该方法在确定门槛值时比较麻烦,需要统计的数据也比极大值分布法多,在实际操作中要比极大值分布法复杂。

图11 广义Pareto法参数图解法Fig.11 Graphic method of generalized Pareto distribution parameters
4 含显微孔洞铸件疲劳寿命预测方法
铸件中显微孔洞缺陷对疲劳寿命影响较大,研究发现疲劳失效裂纹优先在表面或者近表面微孔洞处萌生,在内部微孔洞萌生裂纹时往往孔洞尺寸较大。同时孔洞的形状和位置会影响裂纹的扩展方向和扩展速度,在载荷循环初期内部和表面孔洞的裂纹扩展速度相差不大,但随着循环进行,差异越来越大,最终表现为由表面或者近表面孔洞引起疲劳失效。很多学者研究了显微孔洞特征参数与疲劳寿命之间的关系,本节按照显微孔洞特征进行分类,介绍了考虑不同特征的铸件疲劳寿命预测方法。
4.1 考虑尺寸特征的铸件疲劳寿命预测方法
显微孔洞尺寸特征尤其最大尺寸可以作为典型特征来评估铸件的疲劳寿命,但是只有尺寸大于一定临界值的显微孔洞,才会对疲劳寿命产生影响。宋哲等[17]认为7020铝合金中临界尺寸为30 μm,Buffiere等[23]认为Al-Si7-Mg0.3铸造铝合金中临界尺寸为50 μm。
Y.Murakami[44]最早将孔洞在垂直于载荷方向上最大投影面积的开方等效成孔洞的尺寸,较为方便地构建了孔洞尺寸特征与疲劳寿命的关系。Yi J Z等[46]将孔洞尺寸当成初始裂纹长度a0,通过Paris公式预测了含孔洞A356-T6铝合金的疲劳寿命。随后Yi J Z等[29]认为Paris公式针对长裂纹提出,不适合显微孔洞这样的小裂纹,应该采用基于微观组织结构的位错模型计算裂纹萌生寿命Ni,采用小裂纹扩展公式计算裂纹扩展寿命Np,则疲劳寿命Nf=Ni+Np,预测结果与试验结果吻合较好。Ni与Np的计算公式如式(5)~式(6)所示,其中,C0,α,β和k0为材料参数;kσ与微孔洞等效尺寸有关;λ2为二次枝晶臂宽度;σa为应力幅值;σY为材料屈服应力;C,s和t为经验参数。
(5)
(6)
M.Murat[37]利用图12中A356-T6铝合金试验数据,假设孔洞尺寸服从对数正态分布,建立了失效裂纹萌生处孔洞尺寸与疲劳寿命的统计模型,如式(7)所示,该模型计算值与试验值的吻合度高于对数正态分布和Weibull分布的结果。其中,λ和δ为孔洞尺寸对数正态分布参数;B,Ni和m为拟合参数。
P(Nf)
(7)
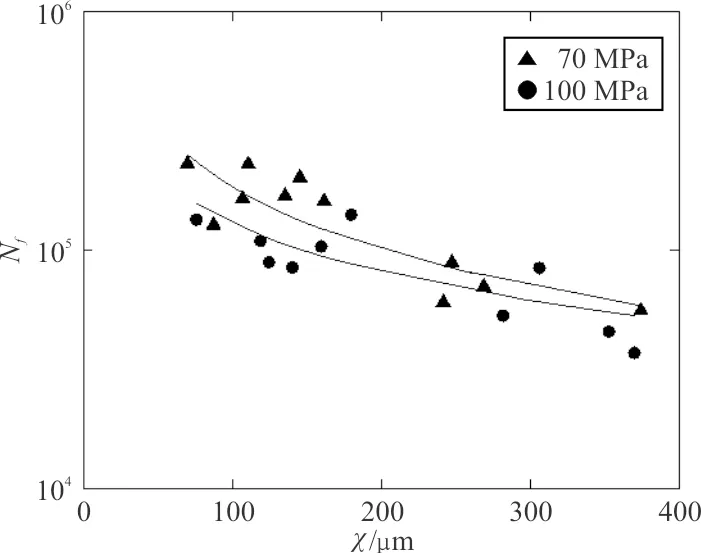
图12 不同应力幅值下最大孔洞尺寸与疲劳寿命关系Fig.12 The relation between the maximum porosity size and fatigue life under different stress amplitudes
4.2 考虑形状特征的铸件疲劳寿命预测方法
张心响[47]通过有限元分析法研究了扁椭球型孔洞椭圆度(长轴与短轴之比)对铸造铝合金疲劳寿命的影响,结果如图13所示,表明孔洞椭圆度与疲劳寿命服从指数分布,椭圆度越大疲劳寿命越低。
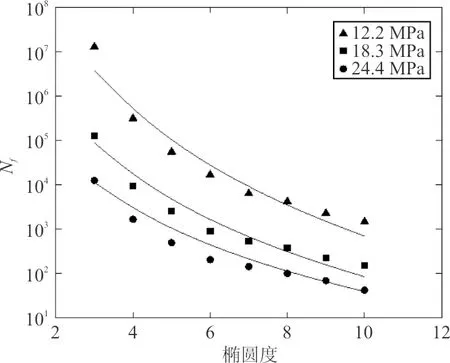
图13 不同应力幅值下孔洞形状与疲劳寿命关系Fig.13 The relation between the maximum porosity shape and fatigue life under different stress amplitudes
K.M.Beckermann等[48]提出了一种考虑显微疏松形状的8630铸钢疲劳寿命计算公式,如式(8)所示,其中,A和n为材料常数;a,a0和af分别为裂纹长度,显微疏松尺寸和裂纹断裂长度;σmax和F分别为最大应力和孔洞圆整度。但该方法不适用于含有较大尺寸复杂形貌的显微疏松缺陷铸件疲劳寿命的预测。
(8)
4.3 考虑空间特征的铸件疲劳寿命预测方法
Vanderesse等[36]通过试验研究了铸造铝合金中失效裂纹萌生处显微孔洞位置与疲劳寿命之间的关系,结果如图14所示,表明失效孔洞距离自由表面越远,疲劳寿命越长。很多学者提出在孔洞尺寸前乘以一个形状因子表明孔洞位置对疲劳寿命的影响,Murakami[49]建议表面孔洞形状因子取0.65,近表面孔洞形状因子取0.5。
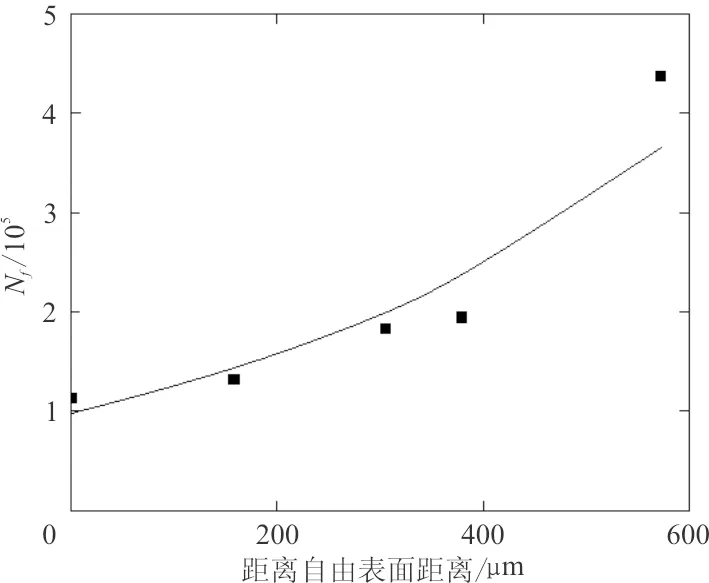
图14 失效裂纹萌生处孔洞位置与疲劳寿命关系(应力比R=-1)Fig.14 The relation between the failure porosity location and fatigue life(stress ratio R=-1)
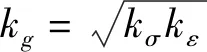
(9)
5 结束语
为数众多的显微孔洞为显微缩松和缩孔,它们具有不规则的三维形貌,内壁粗糙不平整,会引起较大的应力集中,对疲劳寿命的影响更为显著。未来应该进一步明确缩松和缩孔形成的机制,制定相关工艺标准控制其数量和质量,指导铸件的工艺设计。
显微孔洞尺寸特征的分布规律较好地服从对数正态分布,形状特征的分布规律服从Weibull分布,空间特征的分布规律较为复杂。后续研究应该收集显微孔洞尺寸特征、形状特征和空间特征的试验数据,构建孔洞特征参数的多维分布模型,综合评定显微孔洞不同特征参数分布对疲劳寿命的影响。
显微孔洞尺寸特征尤其最大尺寸可以作为典型特征来评估铸件的疲劳寿命,显微孔洞最大尺寸的预测方法中广义Pareto分布的预测结果优于极大值分布法。未来应该进一步研究含孔洞材料疲劳寿命预测模型,明确不同材料显微孔洞临界尺寸,使得最大尺寸的预测结果有明确比较对象,指导铸件的结构设计。
含显微孔洞铸件的疲劳寿命预测模型还不成熟,目前研究主要集中在实验定性和宏观唯象模型,已有的定量预测模型主要关注的是简单载荷下显微孔洞的尺寸特征,复杂载荷下考虑形状和空间特征、以及孔洞间相互影响的疲劳寿命预测方法研究较少。后续应该研究显微孔洞在多轴和高温等复杂载荷下考虑不同显微孔洞特征参数、以及不同孔洞间相互影响的疲劳寿命定量预测模型。
孔洞导致疲劳失效相关机理的研究主要集中在简单载荷下孔洞处裂纹萌生和扩展,一般认为疲劳失效裂纹优先在表面或者近表面孔洞处萌生,孔洞的形状和位置会影响裂纹的扩展方向和扩展速度。复杂载荷下孔洞导致疲劳失效的机理研究还较少,比如镍基单晶高温合金的疲劳失效机理强烈依赖温度,取向偏离、加载频率等,此时微孔洞的疲劳失效机理有待进一步研究。未来可以依靠先进光源展开原位疲劳实验或者分子动力学仿真来研究复杂载荷下孔洞疲劳失效的微观机理。
