基于机器学习的整体穿刺加压参数预测方法

杨景朝， 蒋秀明,2， 董九志,2， 陈云军， 梅宝龙

(1. 天津工业大学 机械工程学院， 天津 300387； 2. 天津工业大学 天津市现代机电装备技术重点实验室，天津 300387； 3. 天津工业大学 电气工程与自动化学院， 天津 300387)

整体穿刺是制造立体织物的一种技术，最早由美国AVCO公司研究成功[1]。立体织物的密度对复合材料的性能有重要影响[2]，整体穿刺加压密实过程中碳布平均层高要控制在合理工艺要求范围内。国内朱建勋团队最早在2003年研制成功了液压驱动整体穿刺机[3]；为提高设备自动化程度及控制精度，2013年南京玻璃纤维研究院与江苏机械研究设计院合作使用可编程逻辑控制器(PLC)和触摸屏对整体穿刺机进行了技术改造[4]。使用油缸驱动整体穿刺机精度易受油温影响，且适用范围受到一定限制，2015年天津工业大学团队研制由电动机驱动整体穿刺样机[5]，具有较高的重复定位精度，实现了对正交叠层机织碳布进行整体穿刺与加压密实功能。以上研究中使用PLC闭环控制、自适应PID 控制算法等提高了加压过程的控制执行精度，但未考虑穿刺模板离开后织物存在反弹情况。

平均层高波动范围较大可导致产品一致性较差，立体织物纤维密度的变化也会影响产品的热力学性能[6]。周钰博等[7]采用4种丝束轨迹特性函数和 2种丝束截面建立了8种穿刺织物结构的三维数字模型。立体织物的不同的工艺参数(如碳布类型、加压间隔、当前层数等)组合时，需要通过加压和时间组合实现控制目标，参数之间的建模涉及纤维材料学、弹性力学、控制工程、理论力学等多个学科，尚无一套成熟的理论模型可较好地表征这个过程。

机器学习理论在金融、生物、医疗、健康、营销等研究领域的应用已取得了巨大的成功[8]。智能制造系统可通过机器学习技术发现大量基础数据背后的规律，机器学习的模型是整个学习过程取得成功的关键[9]。线性模型简单、快捷，可根据高等数学、概率论等充分解释预测模型是如何影响输出结果的[10]；然而现实环境中的很多问题是很复杂的，各因素之间同时存在着线性和非线性关系[11]。研究中仅使用线性模型进行回归分析有很大的局限性，对比线性和非线性不同模型的预测性能，本文提出基于机器学习理论对整体穿刺加压参数进行实时预测的方法,通过训练并优化出1个能有助于降低产品平均层高波动范围的预测模型，部署到生产实验环境中后可根据累积数据不断自学习，持续动态优化对加压参数的预测性能。

1 整体穿刺加压参数预测建模

1.1 整体穿刺工艺流程

正交叠层机织碳布的整体穿刺过程包含Z向钢针布放、整体穿刺、加压密实、钢针置换等环节[12]。碳布置于Z向钢针矩阵上端，在穿刺模板推动下，与Z向钢针矩阵整体穿刺，并沿钢针下移、加压密实。重复以上过程至设定高度后，再由碳纤维逐一替代Z向钢针，制成整体穿刺预成型体[13]。整体穿刺立体织物工艺流程如图1所示。

天津工业大学研制的数字化整体穿刺样机采用电动机驱动曲轴，带动穿刺孔板沿定位光轴上下往复运动[5]，在整体穿刺过程中需要对碳布加压保持一段时间，以确保整体穿刺的立体织物平均层高满足工艺要求。加压密实结构如图2所示。

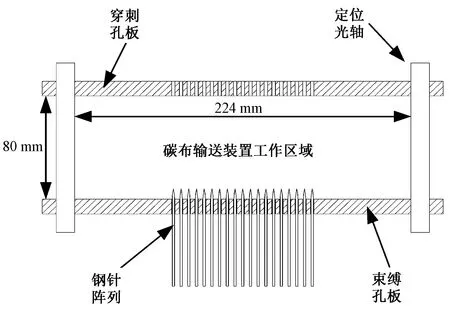
图2 整体穿刺加压示意图Fig.2 Schematic diagram of pressurized compaction and integrated piercing

1.2 基于机器学习的参数之间关系建模

整体穿刺过程中积累了大量的生产数据，产品生产过程中参数列表为：产品编号、碳布类型、助剂类型、加压循环、加压间隔、当前层数、压力增加、压力设定、时间增加、时间设定、当前高度值、平均层高。其中“压力设定”“时间设定”为整体穿刺的加压控制参数，其他为工艺参数。为方便研究将参数列表按顺序定义，如表1所示。

预测压力值时将参数“压力设定”定义为输出特征y，其他参数为输入特征x；预测保压时间时将参数“保压时间”定义为输出特征y,其他参数为输入特征x。引入机器学习中的有监督的学习方式，通过对现有数据集的学习，试图学得一个函数关系f:X→Y,确保f(x)可以很好地预测对应的y,即

表1 机器学习建模变量定义Tab.1 Definition of modeling variables for machine learning

注：m为样本数量。

y=f(x)

式中：x为输入特征；y为输出特征；f为映射函数。样本的输出特征变量是连续的，可以将此问题转化为机器学习中监督学习的回归问题。监督式机器学习流程如图3所示。

图3 监督学习流程示意图Fig.3 Schematic diagram of supervised learning process

使用训练好的机器模型进行预测时，参数“平均层高”的取值为工艺控制目标值k，其他输入参数从可编程逻辑控制器中实时采集获得。

1.3 学习算法的评估指标和方法

为研究整体穿刺过程中机织碳布的压缩性能，选用八枚三飞经面缎纹碳布进行正交叠层整体穿刺加压实验，并将加压参数和碳布层高数据实时保存到数据库中，机织碳布整体穿刺成预制体后在数据库中形成一个完整的数据样本。每个预制体整体穿刺过程的数据样本可在Python中转换为一个训练样本，从中选择50个样本作为训练样本，20个样本作为试验样样本。

欧洲化妆品及其他商品有效性评估专家机构（EEMCO）关于皮肤颜色评估指导指出，计算 ITA°似乎是安全预测用于确定MED的紫外线剂量范围的最准确方法。数字颜色比语言更精确地表达颜色，目前的仪器方法已被证明既敏感又可靠。而目前ITA°与MED的相关性数据但在世界范围内已经引起重视，但在中国人群特别是南方人群中目前文献还比较少，数据来源于外国，我们将具有非常大的局限性，极大地限制了该方法在我国SPF值检测工作中的实际应用。因此，十分有必要进行中国人群皮肤肤色与最小红斑量的相关性的研究，并建立相关的数据库，将有助于更快速、更经济、更准确地进行防晒化妆品防晒指数SPF值的检测。

从50个训练样本中随机抽取1个样本，使用线性回归、5阶多项式线性回归、30阶多项式线性回归3个模型对压力和层高的特征关系进行拟合训练，层数与压力的拟合关系如图4所示。可以看出，线性模型未能很好地拟合训练样本，预测新样本时必然无法准确预测数据，会出现欠拟合；30阶多项式回归模型训练过度拟合了训练数据，包含了部分样本的个性特征或随机噪音，在预测新样本时会导致过拟合。

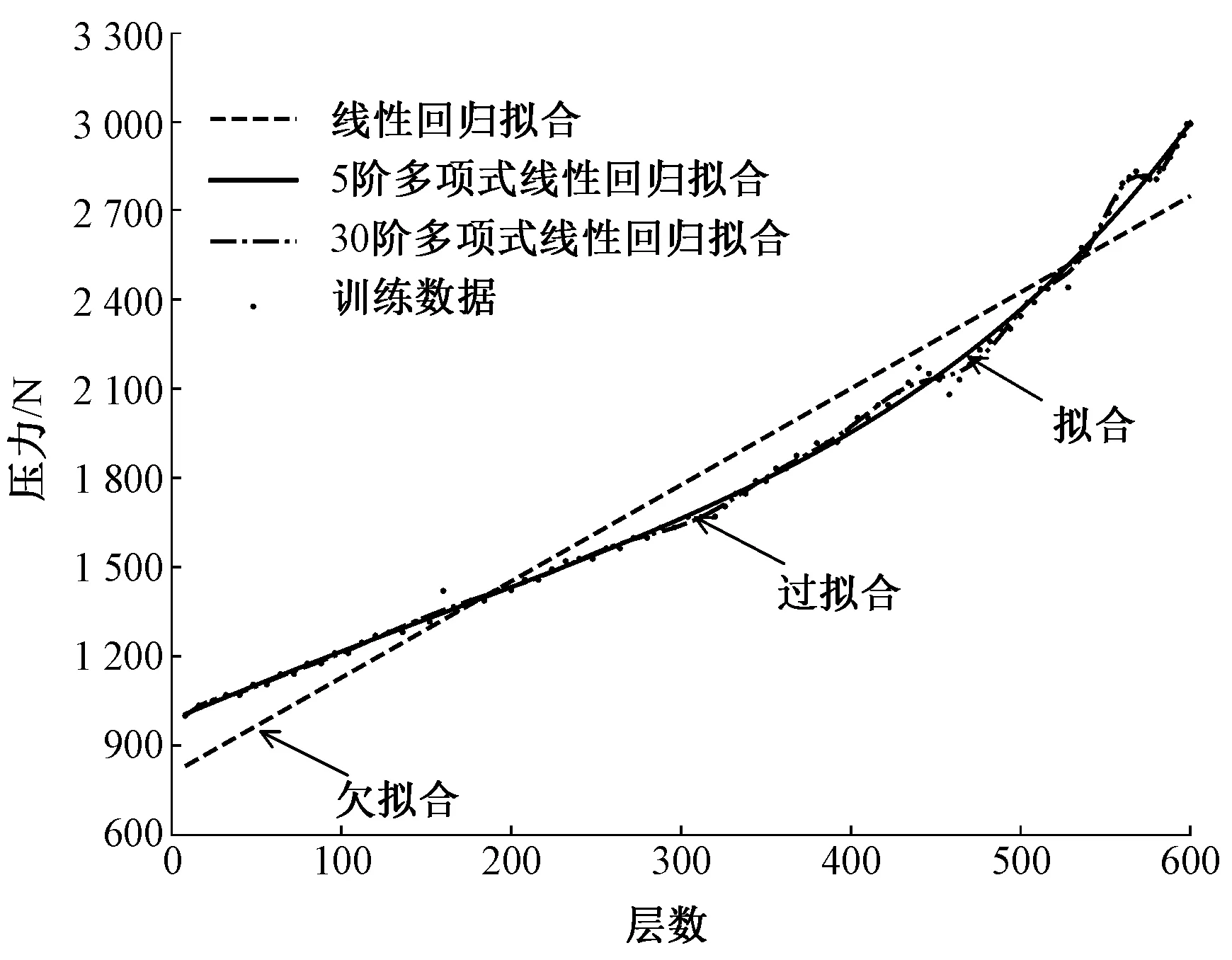
图4 过拟合和拟合对比图Fig.4 Comparison diagram of under fitting and over fitting

针对50个训练样本使用3种回归模型对全部特征数据进行训练，层数与压力2个特征拟合关系如图5所示。

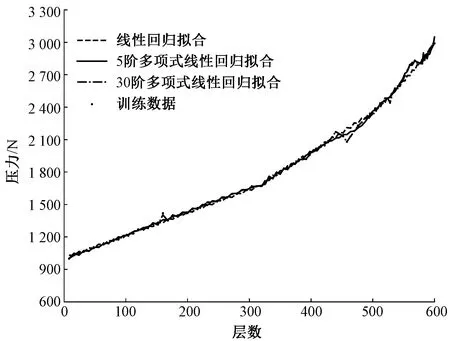
图5 全特征的多模型拟合图Fig.5 Multi models fitting diagram with full features

回归训练中仍存在过拟合和欠拟合的情况，拟合训练中加入了多个特征，对层高与压力的拟合关系产生了影响。图5中的曲线波动幅度与图4相比明显减弱，但二维图对多维度回归关系的展示存在不足，不能直接得出回归拟合效果有本质提升的结论。为解决二维图对包含多特征的拟合关系判断效果不佳的问题，对全特征的多样本模型训练效果引入性能度量。在回归分析中常通过对比新的样本在模型上的预测值和真实值之间的误差，来计算模型性能度量：

式中：f为模型预测函数；y(i)为样本的真实值；f(x(i))为样本的预测值；i为样本序号；m为样本数。50个样本训练后性能度量得分如表2所示。

表2 多样本在3种模型下的均方误差得分表Tab.2 MSE score table of multiple samples based on three models

通过对比图4和表2说明，3种模型在单特征、单样本情况下和全特征、多样本情况下的拟合效果基本一致。

2 整体穿刺加压参数预测模型训练

2.1 基于机器学习的加压参数预测流程

机器学习是致力于研究如何通过计算的手段，利用经验来改善系统自身的性能。计算机系统中“经验”通常以“数据”形式存在，机器学习研究的是计算机从数据中产生“模型”，通过将经验数据提供给学习算法产生模型，在新的数据到来时就可以进行预测或判断[15]。机器学习流程如图6所示。加压参数预测问题可转化为机器学习中的监督学习，从数据集中学习出一个目标函数，当新的数据到来时可根据这个函数预测结果。

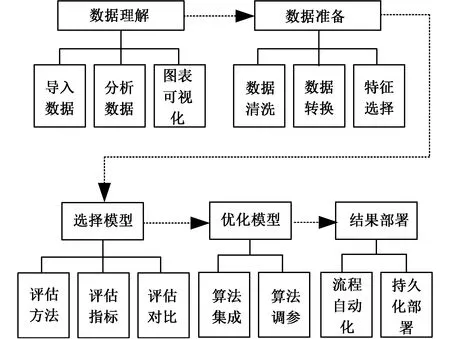
图6 机器学习流程示意图Fig.6 Schematic diagram of machine learning process

2.2 数据特征处理

2.2.1 数据特征转换

通过特征提取得到的未经处理特征存在2个问题：一是定性特征不能直接使用；二是多个特征值不属于同一量纲。按照算法模型分别转换数据有助于提高算法模型的准确度。

表3 数据特征的标签编码Tab.3 Label encoding of data features

使用独热编码将离散特征的取值扩展到欧式空间，离散特征的某个取值就对应欧式空间的某个点。编码后的特征每一维度都可看作是连续的特征，可对其进行归一化处理。对于线性模型来说，独热编码处理可达到非线性的效果。数据特征独热编码后处理的结果如表4所示。

表4 数据特征的独热编码Tab.4 One-Hot encoding of data features

2.2.2 数据特征选择

特征处理时需考虑2个方面：一是特征是否发散，不发散则对样本的区分无意义；二是特征与目标的相关性，相关性高的特征应优先选择。

本文对碳布类型、助剂类型、加压间隔3个特征进行独热编码，特征值只有0和1。计算特征方差后，对于85%以上实取值都是1或0的特征进行移除。用低方差移除特征的处理结果如表5所示。

单变量特征选择是分别单独计算每个变量的某个指标，根据该指标来判断指标重要性，删除次要指标。F回归对矩阵X的第3个列向量X[:,i]和y进行计算，其值越大相关性越强。F回归公式为

表5 移除低方差的数据特征Tab.5 Removing data features with low variance

式中，len(y)为计算列向量y的元素个数。ρi使用如下公式进行计算：

式中：mean(X[:,i])和mean[y]分别为x和y的平均值；std(X[:,i])和std(y)分别为x和y的数据的标准差。

用皮尔逊系数进行特征选择的标准如表6所示。

表6 皮尔逊系数相关程度分类表Tab.6 Correlation degree classification table of Pearson coefficient

综合考虑皮尔逊系数和F回归2种标准作为单变量特征选择的标准，处理结果如表7所示。

表7 单变量特征选择处理结果Tab.7 Processing results of univariate feature selection

2.3 模型选择

模型选择是从成熟算法中选取适合当前项目需求的算法并建立模型，一般通过性能度量对模型的泛化性进行评估。在scikit-learn中，不使用成本函数来表达模型性能，而使用分数来表达，分数值在[0,1]之间，数值越大说明模型准确性越好。本文研究中评估模型用到均方误差(MSE)、平均绝对误差(MAE)、R2这3种评价标准，MAE和MSE越小，R2越大，则说明预测模型描述实验数据具有更好精确度。对4种线性回归算法线性回归、岭回归、套索回归、弹性网络回归和2种非线性算法K近邻和支持向量机进行评估，结果如表8所示。

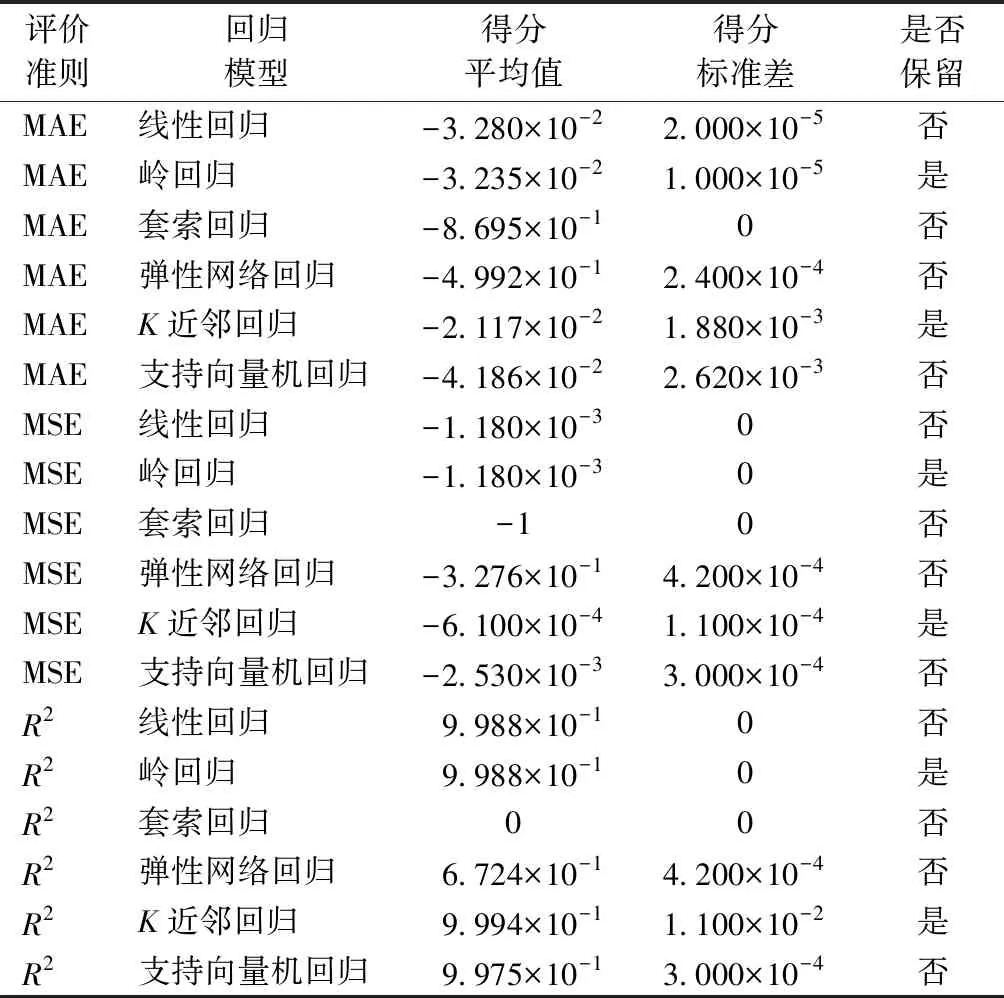
表8 6种模型在3种准则下的评估矩阵Tab.8 Evaluation matrices of six models under three kinds of criteria

根据预测性能得分，保留线性算法的岭回归和非线性算法的K近邻回归，为观察得分的分布情况，对 2种保留模型预测得分做箱线图，结果如图7所示。可知，K近邻回归的偏差小于岭回归，K近邻回归的方差大于岭回归。说明K近邻回归整体表现优于岭回归，选择K近邻回归为基学习器。

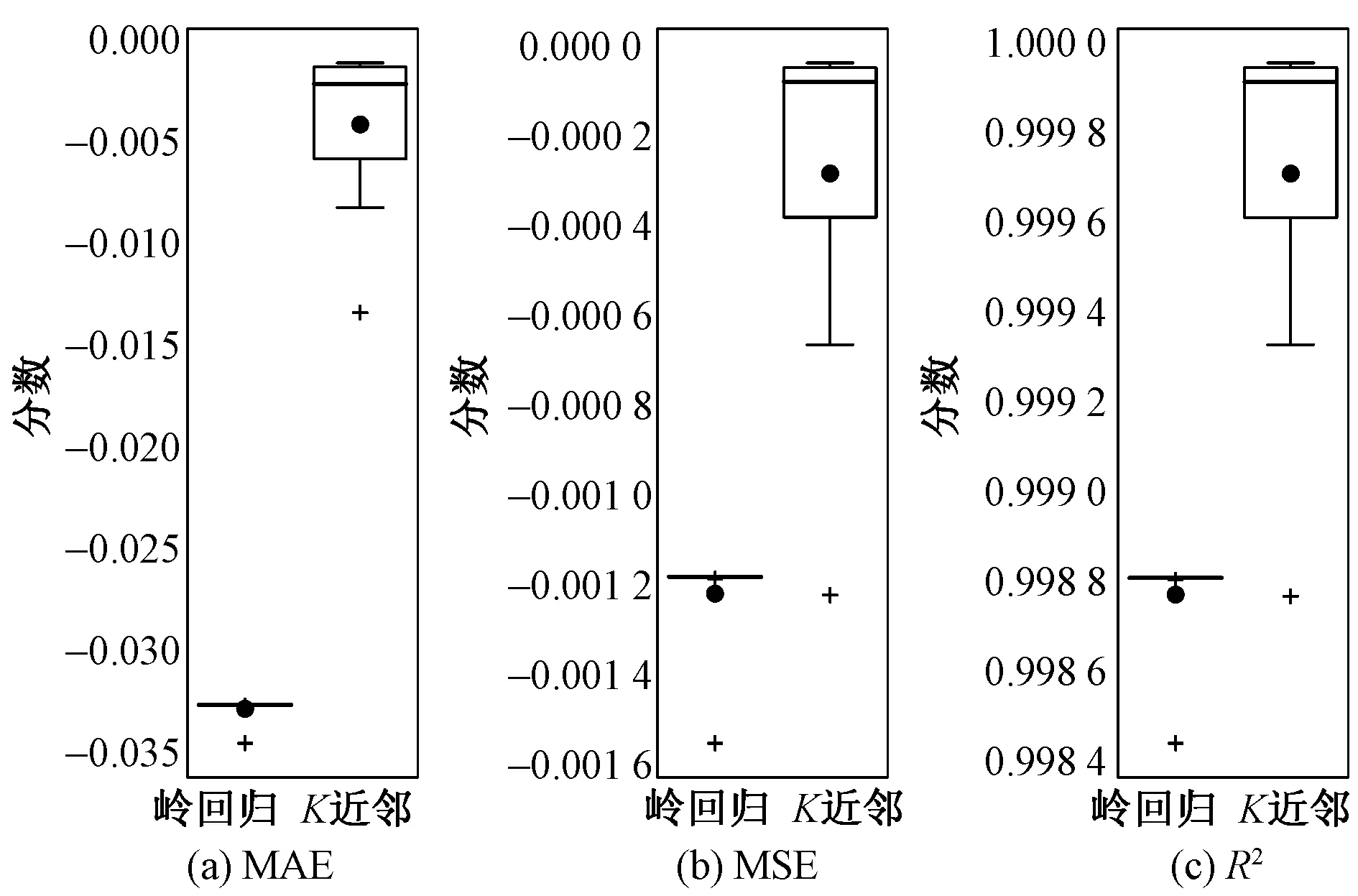
图7 2种模型在3种评估准则下的箱线图Fig.7 Box Line chart of two models under three kinds of criteria

2.4 优化模型

机器学习中可通过装袋、提升等集成算法提高模型的性能[15]。集成算法通过构建多个学习器来完成学习任务，一般结构是先产生1组个体学习器，再用某种策略把他们组合起来。装袋(Bagging)算法适用于强模型，方差较大偏差较小的情况。Bagging算法采样出T个含m个训练样本的采样集，对每个采样集训练出1个基学习器，回归预测中采用平均T个基学习器预测结果的方法。使用集成算法训练后预测性能评价得分如表9所示。

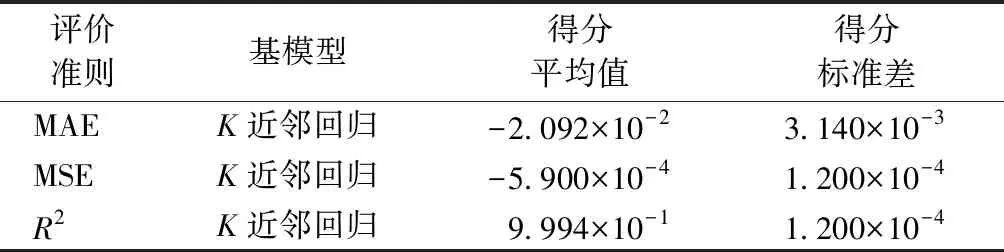
表9 集成算法提升模型预测性能的结果Tab.9 Improved results of model prediction performance using integrated algorithms

3 参数预测模型的实验验证

机器学习模型序列化部署到Web API(网络应用程序)服务器上，通过实验可验证预测模型的准确性和泛化性能，机器学习模型可为整体穿刺过程提供加压参数的实时预测服务。模型部署过程中序列化和反序列化模型时，需要使用相同的Python、SciPy、scikit-learn类库版本；如需在scikit-learn中或其他平台重现这个模型，则需要手动序列化算法参数。

3.1 控制参数预测的实验参数与设备

机器学习预测模型为整体穿刺提供加压参数实时预测服务，机器学习预测方法在经典PID闭环控制的基础上考虑了碳布反弹动态影响因素。工艺要求加压循环过程中压力值和保压时间依次交替增加，在奇数加压周期保压时间不变，压力值可增加；在偶数加压周期压力值不变，保压时间可增加，平均层高设定目标为2.5 mm。实验工艺参数如表10所示。

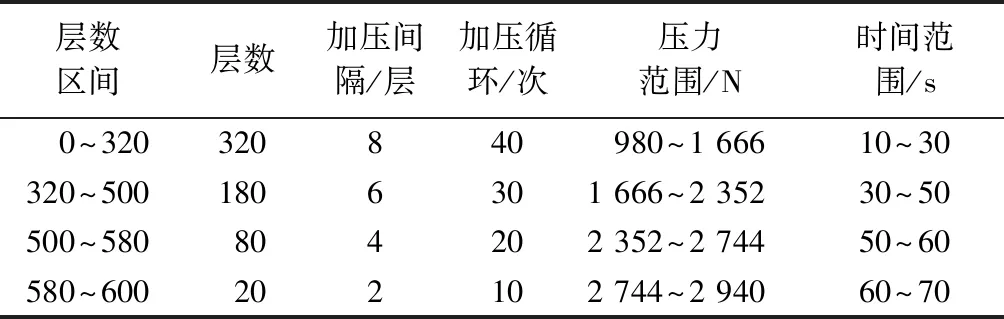
表10 整体穿刺加压预测的工艺参数Tab.10 Process parameters of integrated piercing pressure prediction

整体穿刺机加压参数预测系统及硬件如图8所示。

图8 整体穿刺加压参数预测系统Fig.8 Parameter prediction system of integral piercing pressure. (a) System architecture;(b) Machine

PLC控制伺服电动机并实时获取传感器数据，上位机采用ModBus_TCP协议与PLC通信，上位机调用Web API接口，Web API反序列化预测模型并加载上位机提供的实时工艺参数，得到预测结果反馈给上位机软件，上位机软件按工艺控制规则处理后下发PLC执行，数据自动保存到MySql数据库。

3.2 实验结果分析与讨论

选取经典控制方法50个样本数据和机器学习方法20个样本的加压过程平均层高数据。基于matplotlib绘制了使用机器学习前后加压循环平均层高多样本均值变化趋势，如图9所示。

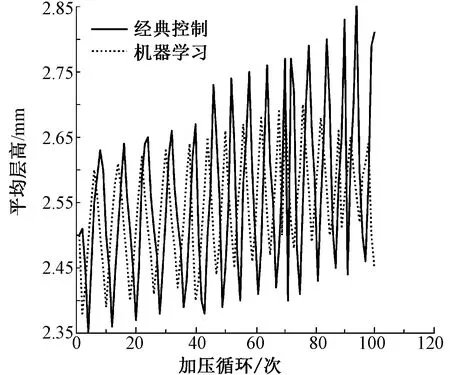
图9 机器学习预测模型前后的平均层高Fig.9 Comparison of average layer height before and after machine learning prediction model

分析加压参数对整体穿刺过程中产品密度一致性的影响，由图9可知，平均层高在工艺目标2.5 mm上下波动且随层数增加逐渐增大，其波动范围反映了使用机器学习方法前后控制精度方面的差别。从曲线可看出，使用预测模型控制先于经典控制方法对生产参数变化趋势做出反应，使得最终产品的平均层高均值明显低于经典控制方法。

使用Seaborn的displot绘制，并利用机器学习前后的立体织物平均层高分布规律直方图和kde核函数估计图，结果如图10所示。

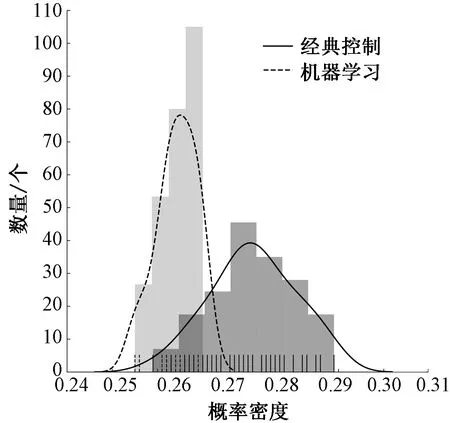
图10 机器学习预测模型前后产品平均层高Fig.10 Comparison of average layer height before and after machine learning prediction model

分析机器学习方法对控制平均层高稳定性的效果，由图10可知，立体织物平均层高的数据分布基本满足正态分布，使用机器学习预测加压参数方法后，样本平均层高的均值公差从12.0%降低到了6.8%，标准差(σ)由0.008 3降低到了0.006 6；分布曲线在均值(μ±σ)附近有拐点。使用该预测加压参数方法后提高了产品平均层高控制的稳定性和产品一致性。

4 结束语

本文基于scikit-learn机器学习类库训练了1个可对整体穿刺过程加压参数进行实时预测的模型，并部署到生产环境为PLC提供加压参数实时预测服务。实验结果表明，机器学习方法应用到整体穿刺控制中，提升了平均层高的控制精度和产品一致性。机器学习理论与传统纺织设备的结合对于推进智能制造具有重要意义，兼具学术研究和产业应用价值，但基于监督式的学习方式对于训练样本的数据质量要求较高，预测模型迁移和扩展时受到一定限制。

FZXB