45钢冷滚打成形Johnson-Cook本构模型参数标定及修正方法

2019-08-29杨明顺李嘉伟崔莅沐

西安理工大学学报 2019年2期

黄赓,李言,李龙,杨明顺，李嘉伟，陈鑫,崔莅沐

(西安理工大学机械与精密仪器工程学院，陕西西安710048)

冷滚打是利用金属在冷态下具有一定的塑性变形能力，使用具有一定形状的滚打轮使工件局部累积变形形成最终所需功能表面的一种近净成形方法[1]。目前主要用于传动零件的外齿成形[2]，有别于传统模锻、模压等[3]静态加载成形，冷滚打成形过程的特点是局部冲击加载，增量渐进成形，成形区材料应变速率大，冲击硬化明显，描述材料本构关系时要考虑应变速率效应和硬化效应。

目前对塑性成形的研究方法主要有理论分析、有限元仿真和实验。其中，有限元仿真方法可以直观地获得相关数据，因此得到广泛应用[4-6]。在进行有限元仿真时需要表述金属变形行为的本构模型，常用的模型有Copwer-Symonds (C-S)模型、Zerilli-Amstrong (Z-A)模型、Steinberg-Guinan模型等基于物理本构模型，以及Johnson-Cook (J-C)模型，Cmap-Beel模型，Bonder-Parton (B-P)模型等经验本构模型。其中，J-C本构模型模型结构简单，使用方便，能够较好的描述金属材料的加工硬化效应、应变率效应，相比于其他模型更适用于冷滚打成形过程仿真。张璐[7]利用ABAQUS软件建立了板料、齿条以及齿形的冷滚打有限元模型，并通过ABAQUS软件分析得到了冷滚打成形力并进行了修正；梁小明[8]基于有限元分析理论，对齿条冷滚打成形过程中的回弹问题进行了探究，并分析了残余应力的分布与回弹产生的原因。袁启龙[9]利用ABAQUS软件分析了材料、滚打方式以及滚打公转速度对滚打力的影响。这些研究中所采用的本构模型参数多引用其它加工方法的研究文献或直接通过分离式Hopkinson压杆实验法获取[10]，均针对冷滚打成形过程特点对模型参数进行修正，这直接影响了仿真结果的准确性和可靠性，因此获得针对于冷滚打成形过程材料变形特点的J-C本构模型参数是十分必要的。

针对J-C模型参数的修正方法有反演法和有限元法。董菲[11]基于剪切试验和有限元模拟确定马氏体不锈钢410的J-C本构方程的系数；叶玉刚[12]通过与切削试验作对比，修正了钛合金TC4的J-C本构方程系数；Short[13]基于Levenberg-Marquardt算法修正J-C模型系数A、B、n来求得HY100钢的J-C本构方程系数。目前，涉及冷滚打成形过程中J-C本构模型参数的标定与修正研究尚未见报道。

综上所述，本文以45钢为例，针对冷滚打成形技术的加工特点，通过对静态和动态压缩力学实验，初步拟合出材料J-C本构模型参数[14-15]。以此为基础建立了冷滚打成形的简化有限元仿真模型，利用冷滚打加工实验和有限元仿真结果，采用下山单纯法修正材料J-C本构模型系数，获得修正后的45钢J-C本构模型参数，并将修正前后不同工艺参数下45钢冷滚打的数值模拟结果与实验结果进行对比论证，为建立更为精确可靠的冷滚打成形有限元模型提供了材料参数的确定和修正方法。

1 冷滚打的成形原理及J-C本构模型参数的修正方法

1.1 冷滚打的成形原理

冷滚打成形基本原理见图1，滚打轮通过中心轴安装在支撑轴上，并可绕自身的轴线转动。当支撑轴在中心主轴的带动下高速旋转时，该运动实现滚打轮的公转，主轴每转一转，滚打轮对工件击打一次，击打工件时，在摩擦力的作用下滚打轮挤压并磙碾工件表面，工件不断进给的过程中使每次击打造成的塑性变形量逐步积累，最终在工件表面形成所需廓形。

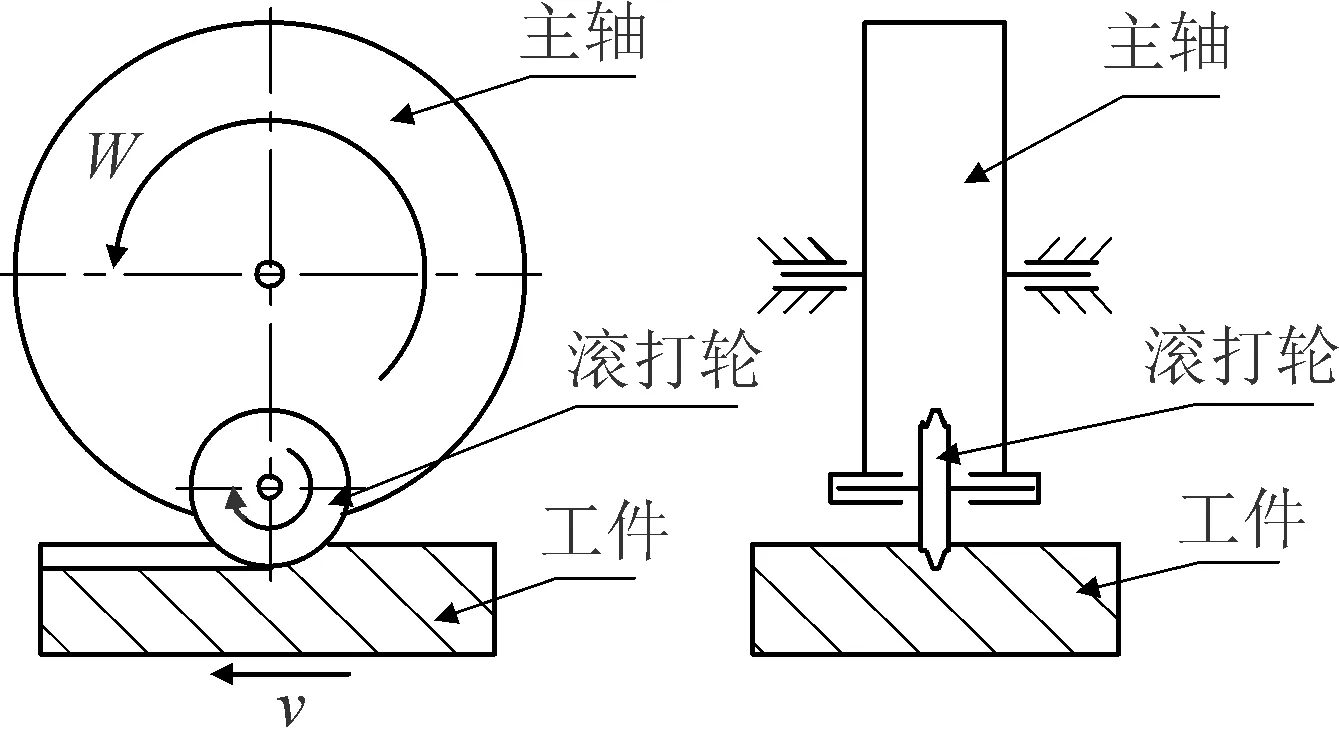
图1 冷滚打成形原理示意图Fig.1 Schematic of cold roll-beating

由冷滚打成形原理可知，冷滚打成形过程材料的变形特点是局部冲击加载，多次加工硬化。考虑到材料在成形时变形主要为挤压变形，因此现有研究中采用的J-C本构模型参数多直接通过分离式Hopkinson压杆实验法获取，但冷滚打成形过程中工件材料的实际受力情况复杂，不仅有压应力，齿壁两侧还受有拉应力作用，变形区和待变形区还存在切应力，因此直接通过分离式Hopkinson压杆实验法获取J-C模型参数，必须进一步的修正才能保证仿真结果的准确性。

标准J-C模型如下：

(1)

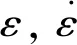
由冷滚打成形原理可知，滚打轮与工件间歇接触，且接触时间很短，摩擦方式又主要为滚动摩擦，因此单次成形区域小，变形和摩擦所产生热量少且很快传到于工件未变形区。因此成形过程引起的温度效应可以忽略，取参数m为常数1，得到简化后的J-C模型形式为：

(2)

1.2 J-C本构模型参数的修正方法

本文采用多元函数的下山单纯形法对J-C本构模型参数进行修正。该方法由Nelder和Mead提出，是一种适用于优化多维无约束问题的数值方法。其优点是稳定性好，适用范围广，搜索阶段效率高[16]。采用此算法优化J-C本构模型参数的流程图见图2。

图2 J-C本构方程参数修正流程图Fig. 2 Flow chart of parameter correction of J-C constitutive equation

以J-C本构模型中的4个参数A、B、C、n为自变量，分别对应向量x中的(a1，a2，a3，a4)，定义目标函数为：

(3)

选定5个顶点作为初始单纯形点；首先以通过分离式Hopkinson压杆实验所获得的参数作为初始顶点，然后初始顶点向量中的每个分量分别乘以一个系数r来得到剩余4个顶点。

计算目标函数f(x)在这5个顶点上的值；fi=f(x(i)),i=0,…4：

(4)

式中：x(L)是最好的点，x(H)是最坏的点，x(G)是次坏点。

新的一个单纯形中应保留初始单纯形点中的最好点x(L)，并通过引入的一个新点x(N)去代替最坏的点x(H)来构造新的单纯形或收缩初始单纯形中除最好点x(L)外的其余4点来构造新的单纯形。

下面是新单纯形构造的具体方法，首先应引入新点x(N)，由式(5)求得除去初始单纯形中最坏点x(H)以后的4个点的重心点x(C)，再根据式(6)求x(H)关于x(C)的反射点x(R)。

(5)

x(R)=(1+a)x(C)-ax(H)

(6)

式中a为给定的反射系数，a>0。

计算fR=f(x(R))并与fL进行比较，根据两者大小分两种情况分别处理。

1) 若fR≤fL，表明反射成功，先按式(7)进行扩展，求得x(E)。

x(E)=γx(R)+(1-γ)x(C)

(7)

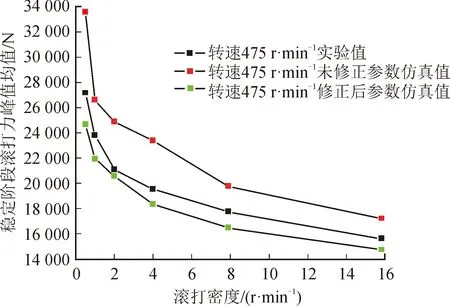
式中γ为给定的扩展系数且γ>1。此时若fE

2)若fR>fL，此时如果fR

x(N)=βx(R)+(1-β)x(C)

(8)

式中β为收缩系数，0<β<1。

此时我们对新点x(N)进行有效性判断，若fN

(9)

将生成后的最好点的参数，带入仿真软件ABAQUS中计算。当实验所测滚打力和仿真计算滚打力的误差小于10%时停止迭代，此时所得参数即为最终修正参数。

2 冷滚打仿真模型建立和实验

2.1 J-C本构模型参数初始值确定

45钢为优质碳素结构用钢，广泛应用于各种传动零件。因此本文以45钢为例，进行了J-C本构模型参数的修正。本文中45钢经过调制处理。

首先对材料本构模型参数进行初始标定。通过静态压缩实验和分离式Hopkinson压杆实验可获得材料J-C本构模型的各个参数[17]。所用设备为电脑式伺服控制材料试验机(MTS机)和分离式Hopkinson压杆，分别见图3和图4。

图3 电脑式伺服控制材料试验机Fig.3 Computer servo control material testing machine

图4 分离式Hopkinson压杆Fig.4 Split Hopkinson pressure bar

通过静态试验和分离式Hopkinson压杆实验得到45钢的静态应力-应变曲线和动态压缩试验应力-应变曲线，见图5和图6。

图5 45钢静态压缩试验应力-应变曲线Fig.5 Stress-strain curve of 45 steel under static compression test

图6 45钢动态压缩试验应力-应变曲线Fig.6 Stress-strain curve of 45 steel under dynamic compression test

由静态和动态应力-应变曲线可得简化后J-C本构模型为：

(10)

2.2 冷滚打仿真模型的建立

在ABAQUS中构建了如下简化的冷滚打数值计算物理模型，见图7。

图7 数值计算物理模型Fig.7 Physical modelfor numerical calculation

为提高仿真效率，该模型将实验中的单滚打轮增加为4个并均匀分布在主轴周围。在实际成形过程中滚打轮的强度远大于工件，所以在数值计算物理模型中设滚打轮为解析刚体，滚打轮半径为25 mm，公转半径为74 mm。计算模型工件的长宽高分别为40 mm×14 mm×10 mm，在工件侧壁施加限制滚打轮轴向自由度的边界条件，底部施加限制滚打轮径向自由度边界，采用C3D8R单元进行结构化网格划分，单元边长为0.2 mm。

2.3 冷滚打实验

通过对卧式铣床进行改造以实现冷滚打成形实验。图8即为改造后的冷滚打成形实验设备，其中滚打轮采用20CrMnTi，通过调制渗碳处理,半径和公转半径分别为25 mm和74 mm，冷滚打过程中的滚打力通过三向力传感器(PCB261A03)测量出。图9为冷滚打成形后的工件。

图8 冷滚打实验平台Fig.8 Experimental platform for cold roll-beating

为了得到能够更加稳定可靠进行冷滚打成形仿真的材料本构模型参数，需进行大量实验结果作参考和对比，因此，选取了如表1所示加工参数进行实验，以此为修正45钢J-C本构模型参数提供对比值。取稳定滚打阶段滚打力峰值的均值为实验滚打力。表1给出了不同冷滚打实验工艺参数下的滚打力实验结果(其中滚打密度为转速与进给的比值，表述了单位长度下击打的次数)。

图9 冷滚打成品Fig.9 Cold roll-beating finished product

表1 冷滚打45钢的实验参数

3 J-C本构模型参数修正及结果

3.1 有限元迭代计算

采用未修正的本构模型参数，对表1所列工艺参数的冷滚打成形过程进行有限元计算，图10给出了成形力实验值与仿真值的相对误差。

选取第5、6、12、13、14、15、16、17组这8组误差较大的加工参数下的仿真模型，采用多元函数的下山单纯形法对J-C本构模型的4个参数进行优化后再进行有限元计算，如此迭代计算直到滚打力的有限元计算值和实验值在所规定的容差范围之内，将迭代计算后8组参数下所得J-C本构模型的各个参数分别进行平均即可得到最终J-C本构模型参数。8组成形参数分别迭代计算后所得J-C本构模型参数和最终J-C本构模型参数见表2和式(11)。

图10 未修正仿真滚打力与实验滚打力相对误差Fig.10 Relative error between the simulated roll-beating force and the experimental roll-beating force

实验序号ABnC5503.88544.820.443 70.021 26 465.82546.440.467 40.021 612514.75544.310.435 30.020 213522.00562.060.411 20.021 214551.00524.740.413 70.021 915580.00541.580.416 10.021 316551.00524.740.413 70.021 917514.75544.310.435 30.020 2平均值525.40541.6250.429 60.021 2

(11)

3.2 结果分析

采用迭代修正后的J-C本构模型参数再次对表1中18个工艺参数条件下的冷滚打成形过程进行模拟仿真得到成形过程的成形力，图11，图12，图13分别为转速475 r·min-1，950 r·min-1，1 500 r·min-1，不同滚打密度下实验值与修正前和修正后的本构模型参数的成形力仿真值。

图11 转速475 r·min-1实验值与未修正和修正后仿真值Fig.11 Experimental values of speed 475 r·min-1 and uncorrected and corrected simulation values

从图11～12中可以看出，滚打密度较低时，未修正J-C本构模型参数所计算的仿真力与实验值的相对误差会偏大且未修正J-C本构模型参数所计算的仿真力总体上大于实验所测滚打力。

从图13中可以看出，未修正J-C本构模型参数所计算的仿真力与实验值的相对误差整体偏大且未修正J-C本构模型参数所计算的仿真力全部小于实验所测滚打力。综上可知，未修正J-C本构模型参数在计算低转速，低进给滚打力仿真时优于高转速，高进给加工条件，计算准确性不稳定。

图12 转速950 r·min-1实验值与未修正和修正后仿真值Fig.12 Experimental values of speed 950 r·min-1 and uncorrected and corrected simulation values

图13 转速1 500 r·min-1实验值与未修正和修正后仿真值Fig.13 Experimental values of speed 1 500 r·min-1 and uncorrected and corrected simulation values

图14为修正前与修正后本构模型参数仿真滚打力与实验滚打力的相对误差对比。

图14 修正前、后仿真滚打力与实验的相对误差Fig.14 Relative error between simulated roll-beating force and experimental roll-beating force before and after correction

从图14可看出，采用未修正的J-C本构模型参数，最大相对误差为23%，采用下山单纯形法修正后的J-C本构模型，最大相对误差下降到9.8%。通过计算修正前与修正后参数仿真滚打力的平均相对误差可知，未修正前的平均相对误差值为12.7%，修正后的平均相对误差值为6.64%。为了确定两组参数的稳定性，计算修正前与修正后参数仿真滚打力相对误差值的方差，可得修正前仿真滚打力相对误差值方差为6.44%，修正后仿真滚打力相对误差值方差为1.9%。综上可知修正后的本构模型参数在仿真中更加稳定与准确，大大提高了仿真的精度。