双级矩阵变换器高抗扰性预测电流控制

宋卫章，杜晓斌，贺 瑾，李 希，张 皓，王有云，钟彦儒

(1. 西安理工大学自动化与信息工程学院，陕西西安710048；2. 大型电气传动系统与装备技术国家重点实验室，甘肃天水741020)

根据拓扑结构不同，矩阵变换器可分为两种，即传统矩阵变换器(conventional matrix converter，CMC)与双级矩阵变换器(two-stage matrix converter，TSMC)[1]，相对CMC，TSMC具有控制、换流策略更加简单的优点，是一种比CMC更具有发展潜力的新型变换器[2-4]。

对于传统的交—直—交变换器，为了获得相对稳定的直流侧电压，直流侧一般存在储能电容，虽然储能环节一定程度降低了拓扑整流与逆变两级耦合影响，但这无疑也增大了该拓扑体积，降低了其使用寿命。相比于传统的交—直—交变换器，一体化的TSMC拓扑致使系统前后两级相互耦合影响。此外，在实际工程中，系统往往要求能抵御一定特殊工况影响，如网侧电压突升突降与不平衡、三相负载不对称等等，这类特殊工况对中间无储能环节的TSMC影响尤为突出，而传统空间矢量调制策略实现复杂且前后级之间必须协调控制，该策略并不能提升TSMC对此特殊工况的抗干扰能力。因此，如何在不增加硬件的前提下，有效提高TSMC抗干扰性能，成为目前国内外学者研究的热点之一。

预测控制通过循环矫正开关状态，使期望目标时刻跟踪其参考值，并依据系统预测矢量直接对开关器件进行控制，具有很强的抗干扰性能和很高的动态响应速度[5-7]。文献[5]将包含导通模式检测的预测控制应用于三相功率因数校正(PFC)系统；文献[6]实现了对三相逆变器电压的预测控制，指出预测控制相比于传统调制策略在快速性和抗扰性方面更具优势；文献[7]提出将预测控制用于传统矩阵变换器(CMC)，但CMC与TSMC在电路拓扑构成上不同，故本文与该文献模型预测控制中的开关矩阵模型不同，两者的预测值的计算方式也将不同。文献[8]中，通过对TSMC的电压矢量扇区进行细分，缩短了开关状态的遍历时间，但是由于该方案所选出的开关状态并非全局最优，因此会对系统的输入输出性能产生一定影响。文献[9]针对电网电压不对称等扰动影响，采用双空间矢量预测控制方案对三相调制波进行预测，并取得了较好的效果。该方案虽然省略了PI控制器，但是仍旧保留着传统的调制环节，相比传统的空间矢量(SVPWM)调制其算法复杂程度增加。文献[10]首次提出将预测控制应用于双级矩阵变换器中，在保证输出电流良好跟随性能的同时，使得输入无功功率最小，但是文中只是描述了预测控制用于TSMC的实现方式，并没有对预测控制下的抗扰性能进行研究和验证，也未涉及电网非正常工况时预测控制抗扰性的研究。文献[11]研究了矩阵变换器驱动的永磁同步电机S型滑模观测器无速度传感器矢量控制系统；文献[12]研究了模型预测控制下的间接矩阵变换器驱动感应电机系统，该矩阵变换器以电机为负载，预测控制以输出转矩和磁通作为控制目标，本文与该文献预测控制算法的负载模型和目标函数均不同，同时本文研究工作侧重解决TSMC的耦合影响和弱抗扰性问题，两者研究对象和解决问题均不同。

本文将探索一种适用于TSMC的预测电流控制策略，以离散化数学模型为基础，利用当前时刻的采样值对下一时刻的输入输出电流量做出预测计算，以网侧无功功率最小和输出电流误差作为系统主要控制目标，循环优化开关状态，使其在不同工况下均能确保良好的输入输出性能，提高系统的抗干扰性能。

1 TSMC预测控制

TSMC拓扑结构如图1所示，TSMC由输入LC滤波电路、矩阵整流级、逆变级和负载四部分组成。其中，Sap、Sbp、Scp分别表示矩阵整流级上桥臂开关，San、Sbn、Scn分别表示矩阵整流级下桥臂开关，Sup、Svp、Swp分别表示逆变级上桥臂开关，Sun、Svn、Swn分别表示逆变级下桥臂开关。udc、idc分别为中间虚拟直流侧电压与电流，Lf为线路寄生电感与滤波电感之和，Cf为线路寄生电容与滤波电容之和，Rf为线路和滤波器上等效电阻值之和，Ll为负载电感，Rl为负载电阻。

1.1 原理

TSMC预测控制框图如图2所示。通过检测网侧电压usk、电流isk和输入滤波电容上电压uek，结合k时刻的开关状态Sk获得开关输入电流值iek，再依据TSMC输入滤波器离散数学模型计算网侧电流预测值isk+1，并将此预测值用于计算k+1拍网侧无功功率qink+1大小。通过检测输出电流iok，利用k时刻的开关状态Sk获得输出电压值uok，利用负载离散数学模型计算输出电流预测值iok+1，获得输出电流参考值io(k+1)*与输出电流预测值iok+1的误差，最终与输入无功参考值qin(k+1)*和输入无功预测值qink+1的误差联合成一个品质函数，用于寻求对应的最佳开关状态Sk+1，实现TSMC主功率开关控制。

图2 预测控制框图Fig.2 Block diagram of predictive control

为保证TSMC具有良好的输入输出性能，将系统循环优化的条件设定为[4]：

1) 输入侧无功功率接近于零；

2) 输出电流与参考值的误差接近于零。

1.2 数学模型

为便于构建TSMC数学模型，将三相abc坐标系下的电压电流量转化至两相αβ坐标系下。例如，输出电压uo在abc坐标系下为uou、uov、uow，在αβ坐标系下则可表示为：

uo=uoα+juoβ

(1)

(2)

abc/αβ坐标系下TSMC电压电流表示符号如表1所示，TSMC数学模型可以被分为整流级和逆变级。

表1 abc/αβ坐标系下TSMC电压电流表示符号

Tab.1 Voltage and current signs of TSMC in the

abc/αβ reference frame

1) 建立TSMC的开关模型：

(3)

根据输入输出关系，结合开关状态，TSMC的输入输出电压关系式为：

(4)

其中，T为TSMC的总开关矩阵，T的值由TSMC的开关状态决定。

同理，亦可建立输出电流与输入电流的关系式：

(5)

2) 利用基尔霍夫定律，建立输入滤波器模型：

(6)

(7)

将式(6)、(7)用状态空间方程表示：

(8)

同上，负载的数学模型为：

(9)

1.3 开关状态表

TSMC整流级如表2所示，共有9种开关状态；逆变级如表3所示，共存在8种可能的开关状态。对前后级可能的开关状态进行排列组合，共存在72种可能的开关状态组合。为了保证TSMC整流级输出电压最大化，剔除存在的3个零矢量，此零矢量作用下逆变级输出电压瞬时值为零，故TSMC模型预测控制中仅剩余48种有效的开关状态组合可供选用。

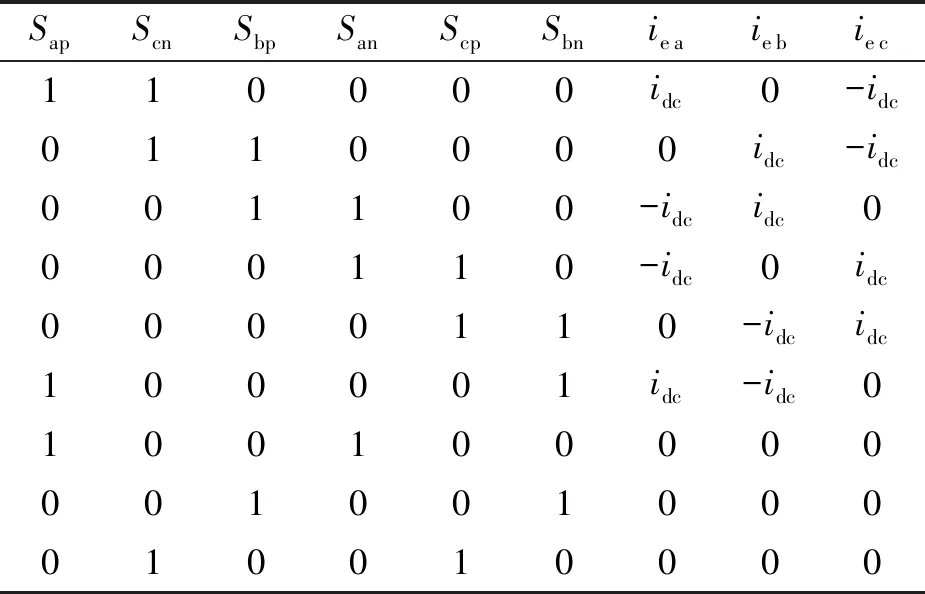
表2 整流级开关状态

表3 逆变级开关状态

注：uuv、uvw、uwu为三相线电压。

1.4 计算预测值

将输入滤波器与负载的数学模型分别离散化。

对式(8)引入前向欧拉方程进行离散化，可分别推导出网侧电流预测值和输入滤波器电容电压预测值：

(10)

C=eATs

(11)

(12)

式中：τ为时间常数；Ts为采样周期。

利用前向欧拉插值法，可得输出电流的导数近似值为：

(13)

将式(13)代入式(10)可得到离散化的负载数学模型：

(14)

由式(14)知，TSMC预测控制算法与负载参数有关，但离散后的负载模型表达式中含有Ts，Ts为小时间常数，故Ts/L1和(R1Ts)/L1在离散负载模型中所占份量较小，于是负载参数变化时预测电流值并未受太大影响，算法对负载变化引起的扰动具有一定自抑制作用，故在负载参数发生变化而又提前未知的情况下，TSMC模型预测控制算法的准确性和可靠性仍较高。

1.5 品质函数

品质函数是对控制目标的直接反映，也是系统循环优化的条件。

将三相输出电流转换到两相静止坐标系中，与参考值作差，获得误差绝对值表达式为：

(15)

式中：ioαk+1、ioβk+1是αβ坐标系中输出电流在k+1时刻的预测值；ioα*、ioβ*分别是其所对应的参考值。

根据瞬时功率理论，将网侧电压电流转换至αβ坐标系下，可知网侧无功功率的预测值为：

(16)

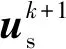
(17)

将输入无功功率参考值设为0，构建无功的误差表达式：

(18)

最后，式(15)、(18)组合成一个品质函数：

(19)

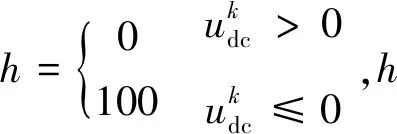
在每个采样周期，将每种开关状态组合代入数学模型，计算出对应的品质函数，最终，选出品质函数最小的开关状态，以此驱动对应开关器件导通。

1.6 权重因子

品质函数中λ是权重因子，在含有多个约束项的品质函数中，λ相当于次要项的加权系数。本文λ决定开关状态的选择对输出电流和输入最小无功功率的重视程度。

当品质函数中有多个不同控制目标时，可以以控制目标为约束对权重因子进行缩小范围选取。本文以输入无功功率与电流参考误差最小为控制目标，通过以下两步来确定权重因子λ的取值范围。

首先，以输出电流控制误差为约束，即以输出电流波形质量为衡量标准，将输出电流总谐波畸变率THD≤5%作为判断条件，用二分法对权重因子的范围进行初选[13]。如图3所示，λ先取0或1，依据仿真，λ=1时输出电流THD=14.5%，THD>5%不满足要求，于是λ取中间值0.5，依靠仿真可知，输出电流THD=10.3%>5%不满足要求，然后确定下次λ的范围为[0,0.5]，以此类推，直到输出电流THD≤5%，最终得到λ的初选范围为0≤λ≤0.016。

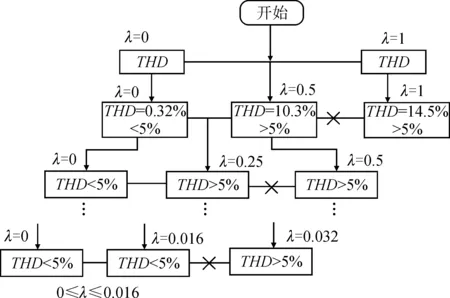
图3 权重因子λ的初选范围Fig.3 Primary range of weighting factor λ

其次，在上一步确定的初选范围[0，0.016]基础上，同时考虑网侧无功功率与输出电流THD，以这两个因素为约束对权重因子细选。将λ从0增至0.016，记录每个λ所对应的输出电流THD与无功功率，将这些数据点绘在一起，可得到如图4所示的曲线，两线相交处即为同时满足输出电流THD与无功功率最小的λ值，由图可知，权重因子λ=0.004 5时可同时满足上述要求。

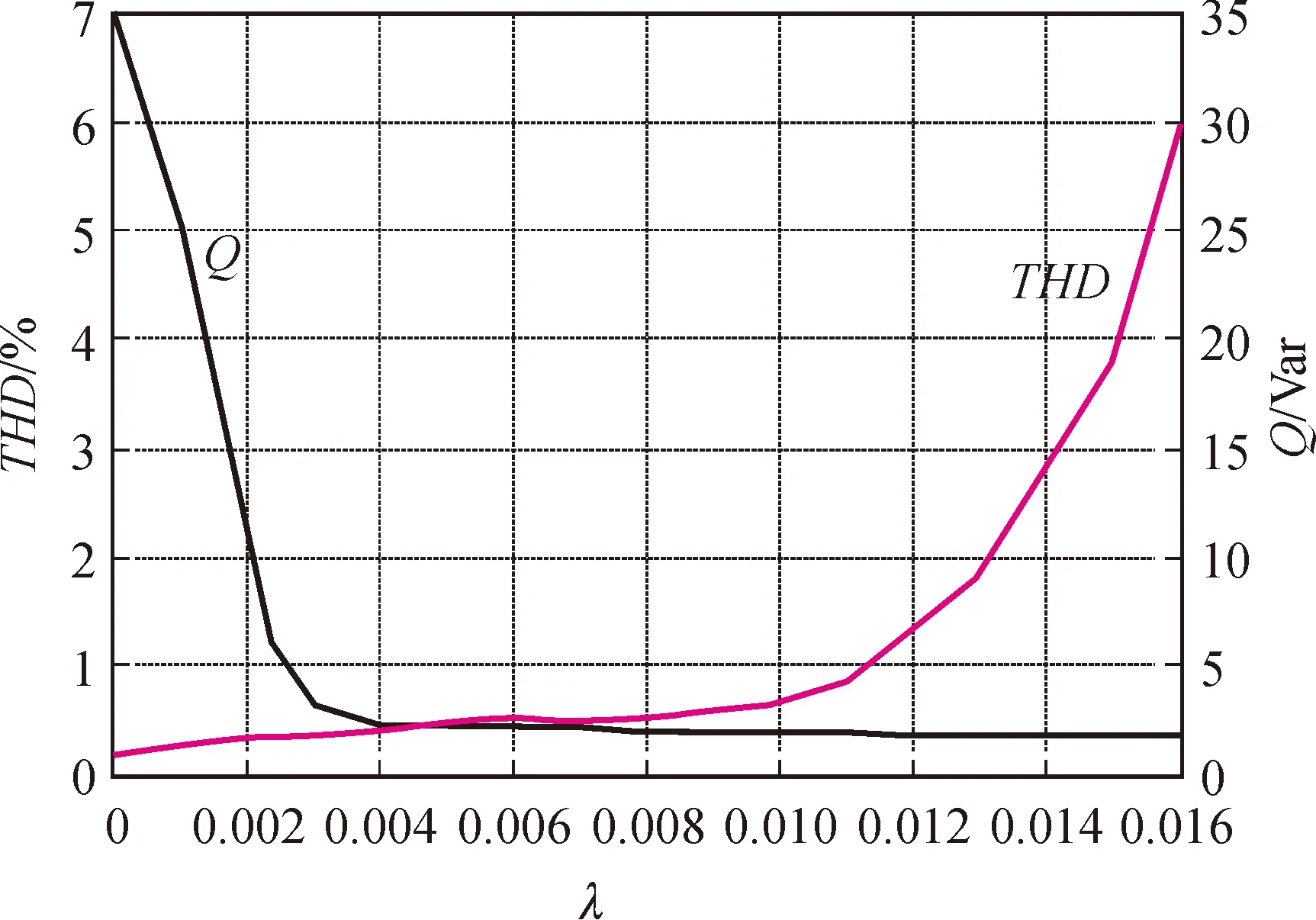
图4 输入无功Q和输出电流THD与权重因子λ的关系曲线Fig.4 Relationship between reactive power Q and THD of output current and weighting factor λ

2 实验验证

为了验证上述方案的正确性和有效性，搭建以数字信号处理器+现场可编程门阵列(DSP+FPGA)为核心控制器，功率450 W的实验样机，其中硬件系统实现框图如图5所示，实验样机如图6所示。表4为实验参数，图7为控制流程图。分别对不同工况下系统所采用的预测控制方案进行实验验证。

图5 TSMC硬件系统实现框图Fig.5 Diagram of hardware system for TSMC

图6 实验样机Fig.6 Experimental prototype

参数名称参数值输入电压100 V/50 Hz输入滤波器Rf=0.5 Ω; Lf=1.2 mH; Cf=2 μF负载Rl=10 Ω; Ll=10 mH权重因子0.004 5采样频率20 kHz死区时间3 μs

图7 预测控制流程图Fig.7 Flow chart of predictive control

2.1 正常工况下预测电流控制验证

将输入无功功率最小与输出电流误差共同加入品质函数进行实验验证，仿真与实验波形如图8所示，其中uuv表示输出线电压。图8(a)、(b)为网侧相电压与相电流的仿真与实验波形，由波形可知，网侧相电流与相电压时刻保持同相位，网侧功率因数接近于1，从而验证了预测控制下TSMC良好的网侧性能。图8(c)、(d)分别为预测控制下TSMC的输出三相电流与输出线电压稳态波形，从波形可看出，三相电流频率为100 Hz，输出纹波较低，稳态性能良好。图9为输出电流频率由6 A、100 Hz阶跃变化至5 A、200 Hz后又恢复至6 A、100 Hz的动态变化仿真与实验波形，由图可看出，输出电流阶跃变化响应快，波形正弦度良好，证明TSMC具有优良的动态性能。

图8 预测电流控制稳态性能验证Fig.8 Predictive control steady state performance verification

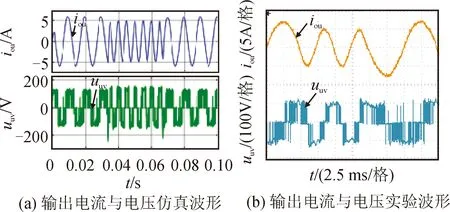
图9 预测电流控制动态性能验证Fig.9 Predictive control dynamic performance verification

2.2 非正常工况下不同策略时TSMC性能对比

在实际工程中，系统往往要求能一定程度抵御非正常工况的影响，为验证TSMC预测控制的高抗扰特性，分别从电网电压不平衡与突升突降、三相负载不对称三方面对TSMC在传统闭环控制与预测控制下的系统抗扰性进行了测试。

考虑到实验的可操作性，三相电网电压分别设置为usa=50V、usb=60V、usc=80V，图10和图11分别为传统控制与预测控制方案下电网不平衡时TSMC波形，其中图10(a)、(b)与图11(a)、(b)分别为传统控制与预测控制方案下的网侧相电压、相电流仿真与实验波形；图10(c)、(d)与图11(c)、(d)分别为传统控制与预测控制方案下的三相输出电流波形。经波形对比可知，三相电网不平衡工况时，传统控制方案对电网不平衡的影响抑制能力有限，需额外增设补偿模块才能消除不平衡的影响。相比于传统控制方案，预测控制始终以输入无功及输出电流跟踪误差为零为控制目标，于是预测控制方案下TSMC仍具有单位功率因数，输出电流跟踪参考，三相输出电流基本平衡，从而验证了预测控制对TSMC网侧电压不平衡的影响具有一定程度的抑制作用，提高了TSMC的抗扰性。

图10 传统控制下电网不平衡时波形Fig.10 Waveforms of traditional control in input imbalance

图11 预测控制下电网不平衡时波形Fig.11 Waveforms of predictive control in input imbalance

图12和图13分别为电网电压由100V跌落至90V时传统控制与预测控制方案下的仿真与实验波形，其中图12(a)和(b)分别为传统控制策略下网侧电压与输出电流波形，由波形知，在电网电压跌落时，传统闭环控制方案虽一定程度抑制了输出电流幅值变化，但却使输出电流波形严重畸变。图13(a)、(b)分别为预测控制下电压跌落时网侧电压的仿真与实验波形；图13(c)和(d)分别为预测控制下电压跌落时输出三相电流、输出线电压的仿真与实验波形。由波形知，预测控制以输出电流误差最小为控制目标之一，即使网侧电压跌落，但输出电流仍能够跟踪参考，仍能使三相输出电流平衡并具有较好的正弦度。由此，相比于传统的PID控制方案，预测控制能更有效地抑制网侧电压跌落对系统的影响，从而使系统具有更强的抗扰性。

图12 传统控制下电压跌落时波形Fig.12 Waveforms of traditional control at voltage drop

图14和图15分别为三相负载RL1=10 Ω、RL2=7 Ω、RL3=6 Ω不对称时的仿真和实验波形，其中图14(a)、(b)和图15(a)、(b)分别为传统控制和预测控制下的网侧相电压、相电流波形；图14(c)、(d)和图15(c)、(d)分别为传统控制和预测控制下的输出三相电流和线电压波形。由波形知，即使在负载不平衡条件下，预测控制下TSMC仍能实现控制目标，相较于传统调制策略，其输出的三相电流幅值更平衡且具有更好的正弦度，使系统具有更强的抵御负载不平衡扰动影响的能力。

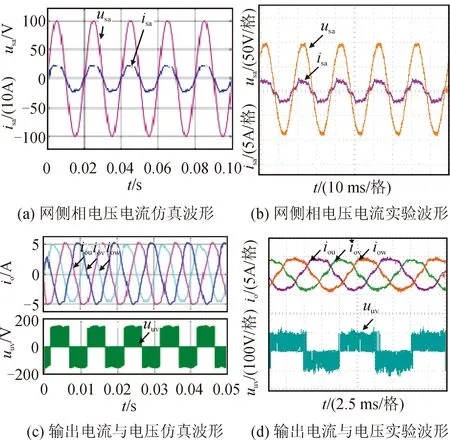
图14 传统控制下负载不对称时波形Fig.14 Results of traditional control under unbalanced load

图15 预测控制下负载不对称时波形Fig.15 Results of predictive control under unbalanced load

3 结 语

本文研究了一种适用于TSMC的预测电流控制，以TSMC离散化数学模型为基础，利用当前时刻的采样值对下一时刻的输入输出电流量做出预测计算，将网侧无功功率最小和输出电流误差作为控制目标，循环优化开关状态，使其在正常和非正常工况下输出电流均能时刻跟随参考给定，提高了系统鲁棒性，降低了前后级耦合影响，并实现了“绿色”网侧性能。此研究对于解决矩阵变换器耦合和弱抗扰性问题具有重要借鉴意义。