基于等效体积单元方法的空心坝工作特性有限元分析

俞昊捷 沈振中 徐力群 张宏伟

(1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学 水利水电学院，南京

210098)

浆砌石坝是砌石块通过砌浆材料黏结砌筑而成的挡水建筑物，在建坝时能够就地取材，建成后则方便溢流，在石料丰富的山区内建坝常选择建造浆砌石坝.红旗渠空心坝是坝腹内设置双孔过水涵洞的浆砌石坝，因其坝腹空心而得名.空心坝坝身可调节河道内来水，坝腹涵洞可运输渠道内来水，该结构顺利解决了红旗渠当地河道与渠道立交的问题.红旗渠空心坝结构特殊，在结合浆砌石坝和涵洞两种水工建筑物特点的同时，也拥有自己独有的结构特点，目前对空心坝工作特性的研究分析较少，这严重制约了空心坝的利用和推广.本文采用均质化理论对红旗渠空心坝的工作特性进行三维仿真模拟计算，为运行多年的红旗渠空心坝的安全评定打下基础，同时也为将来设计、改进和应用新型空心坝提供一定参考.

由于浆砌石坝是由砌石块和水泥砂浆共同砌筑而成，如果采用最原始的离散模型方法建模，势必会导致模型过于复杂、网格剖分工作量大、计算时间过长，甚至可能导致最终的计算结果不收敛.因此，基于均质理论的RVE方法就成为了计算空心坝工作特性的首选计算方法.

1 RVE模拟方法

等效体积单元(Representative Volume Element，RVE)有限元模拟最初被用来预测复合材料的宏观弹性模量，而后在众多砌体结构的计算分析中发挥了重要的作用.基于RVE开展的均质化理论方法不同于离散模型理论方法，均质化理论方法无需根据实际材料的组成创建与真实结构完全一致的模型，也无需在模型中设置所有材料属性，这就使得模型更加简化、剖分网格更加方便，也减少了有限元计算的工作量与时间，但是在计算中依然能够等效地考虑砌体结构所有组成相的材料特性，保证计算分析的准确性[1-10].

RVE的选取一般需要满足以下要求：1)考虑砌体各组分的物理参数；2)考虑砌体内部结构的周期性关系；3)同时满足以上两点的最小结构单元[11].对RVE进行模拟时，在RVE的表面施加均匀应力场或位移场.根据有限元模拟结果整合应力-应变曲线时，曲线中的应力值和应变值均采用平均应力值和平均应变值，平均应力值和平均应变值根据式(1)计算：

其中，V是RVE的体积，σij和εij分别是应力和应变的各个分量[12].

2 RVE有限元模拟

2.1 材料参数

红旗渠空心坝采用杂色人工砌石作为筑坝材料，其主要成分为肉红色石英砂岩和灰白色白云质灰岩，同时夹杂少量的太古界片麻岩，各砌石之间以砂浆填充护砌.在空心坝长期运行过程中，其材料的物理属性将直接影响坝体结构的稳定和安全.文中砌石块与砂浆的材料参数取值见表1[13-14].

表1 材料参数

2.2 RVE的选取

建造空心坝所采用的砌石尺寸要大于普通砖块尺寸，相应地，砌石结构的RVE尺寸也较普通砖砌结构的RVE尺寸更大.空心坝采用的砌筑方式与普通砖砌结构的砌筑方式相似，可以近似地看作“顺砖砌筑”.针对不同砌筑方式，RVE的选取方式存在不同，不同的RVE选取会进一步导致模拟得到的力学参数的差异，但是这些差异在工程范围内是可以接受的[15]，本文选取RVE的结构形式与尺寸大小如图1所示.

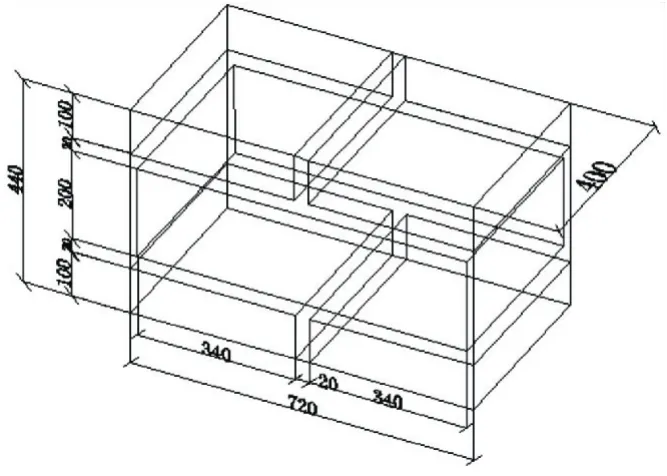
图1 本文RVE的选取方式及尺寸(mm)

由图可见，单块砌石的尺寸取为700 mm×200 mm×400 mm，RVE的整体尺寸取为720 mm×440 mm×400 mm.完成有限元网格剖分后的RVE及各材料组分如图2～4所示.本次剖分RVE采用的网格类型为线性缩减积分网格C3D8R，根据该网格类型能得到精准的位移结果和较为精准的应力结果.RVE有限元网格剖分共2 600个，其中砂浆部分网格920个，砌石部分网格1 680个.

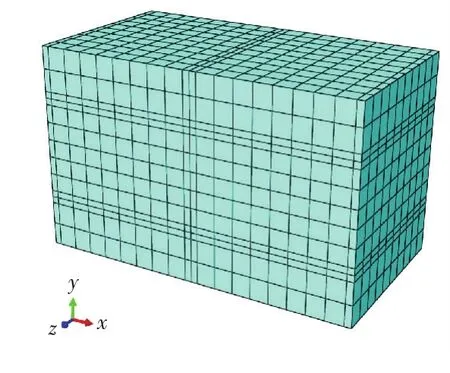
图2 RVE网格剖分

图3 砌石部分网格剖分

图4 砂浆部分网格剖分

2.3 单轴抗压有限元模拟

采用有限元软件ABAQUS模拟RVE单轴抗压试验，在RVE模型的上侧表面施加作用方向为砌体表面指向砌体内部的法向位移荷载，所施加法向位移荷载为-1 m；同时对RVE模型的下侧表面施加相应约束，所施加约束为X、Y、Z三向约束.得到RVE单轴抗压应力-应变云图，并计算得到相应的应力-应变曲线，应力-应变曲线如图5所示，可见RVE在Y方向上的极限抗压强度为5.08 MPa，相应峰值应变为3.11×10-4.

图5 RVE单轴抗压应力-应变曲线

2.4 单轴抗拉有限元模拟

在RVE模型的上侧表面施加作用方向为砌体内部指向砌体表面的法向位移荷载，所施加法向位移荷载为0.001 m；同时对RVE模型的下侧表面施加相应的约束，所施加约束同单轴抗压模拟约束.得到RVE单轴抗拉应力-应变云图，并计算得到相应的应力-应变曲线，应力-应变曲线如图6所示，可见RVE在Y方向上的极限抗拉强度为170 k Pa，相应峰值应变为4.58×10-6.同时可以发现，当应变达到3×10-6附近时，应力-应变曲线的斜率发生了明显的改变，RVE模型在Y方向上的抗拉弹性模量变大.

2.5 纯剪有限元模拟

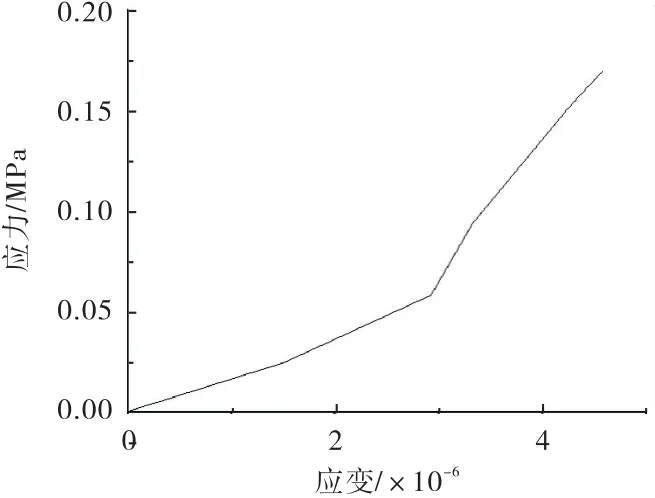
图6 RVE单轴抗拉应力-应变曲线

本文采用沿着砂浆缝的受剪性能来模拟RVE纯剪试验.在RVE模型的左侧上部砌石表面、左侧下部砌石表面和右侧中间砌石表面分别施加作用方向为砌体表面指向砌体内部的法向位移荷载，所施加法向位移荷载为0.01 m.得到RVE在YZ平面上的纯剪应力-应变云图，并计算得到相应的应力-应变曲线，应力-应变曲线如图7所示，可见RVE在YZ平面上纯剪的极限强度为1.96 MPa，相应峰值应变为1.90×10-4.

图7 RVE在YZ平面上纯剪应力-应变曲线

3 空心坝工作性态分析

3.1 工程概况

红旗渠空心坝坝长166 m，底宽20.3 m，顶宽7 m，坝高6 m，坝基埋深1～2 m，坝体整体呈弓形.坝腹双孔涵洞各宽3 m，高4.5 m，洞底纵坡坡率1/1 818.红旗渠空心坝下游侧设有103 m×20 m×1 m的消力池，再下游为干砌大块、片石护坦.空心坝左右岸各设高4.4 m的导水墙，用于引导洪水走向.红旗渠空心坝竣工时的完成砌石方量为16 296 m3，砌石总投工约13万个.

红旗渠空心坝位于山谷地形中，其基础所在地层自上而下划分为3个岩土工程地质单元，分别为淤积填土单元、杂色卵石单元和太古界片麻岩单元.其中，空心坝上游、中部基础均位于卵石层中.本文考虑各地层材料采用弹塑性本构模型，在弹性范围内考虑胡克定律，在弹塑性范围内考虑普遍存在的摩尔-库伦理论，即

其中，c是黏聚力，σ和tanθ分别是法向应力和内摩擦角的正切值.红旗渠空心坝所在各地层力学参数见表2.

表2 各地层力学参数

3.2 有限元模型

红旗渠空心坝三维模型和三维有限元网格剖分如图8～9所示.由图可知，空心坝三维建模中，取沿坝上游指向下游方向为X正方向，空心坝左岸至右岸延伸方向为Y正方向，沿地基竖直向上方向为Z正方向.模型取地基深度15 m，同时取右岸地基延伸范围60 m，左岸地基延伸范围15 m，上游地基延伸范围40 m，下游地基延伸范围30 m.模型包括空心坝坝体、导水墙和下游消力设施，同时包括坝体两侧部分渠道以及相邻山体.有限元计算采用商业软件ABAQUS，本次建模设置网格总数168 732个，采用网格类型为C3D3.

图8 三维模型

图9 三维有限元网格

3.3 计算工况与典型截面

本文针对红旗渠空心坝实际运行情况分析计算3种工况，具体如下：工况1为空心坝正常运行工况，由于空心坝上游侧常年无水，因此该工况下空心坝主要承受的荷载包括结构自重、上游淤积压力、涵洞水压力；工况2为校核工况，该工况下空心坝承受的荷载主要为结构自重、上游淤积压力、涵洞水压力、校核洪水荷载和底部扬压力；工况3为地震工况，该工况下空心坝主要承受的荷载有结构自重、上游淤积土压力、涵洞内水压力和地震荷载[14，16-17].

根据初步计算得到的应力分布情况，选取空心坝典型截面Ⅰ和典型截面Ⅱ如图10中阴影部分所示.

图10 典型截面

3.4 工作特性分析

空心坝在正常运行工况下的计算结果云图如图11所示.

图11 工况1计算云图

由图可知，典型截面Ⅰ的第一主应力最大值出现在上游侧涵洞底部，最大值为45.26 k Pa.典型截面Ⅰ的第三主应力最小值出现在坝基上游侧，最小值为-270.20 k Pa.典型截面Ⅰ最大变形值出现在上游侧涵洞顶部，最大变形值为0.030 mm.同时，典型截面Ⅱ的第一主应力最大值出现在下游侧涵洞底部，最大值为85.94 k Pa.典型截面Ⅱ的第三主应力最小值出现在两个涵洞之间的坝体段，最小值为-600.90 kPa.典型截面Ⅱ最大变形值出现在导水墙斜坡顶部，最大变形值为0.099 mm.

校核工况计算结果云图如图12所示.由图可知，典型截面Ⅰ的第一主应力最大值出现在下游侧涵洞底部，最大值为44.80 k Pa.典型截面Ⅰ的第三主应力最小值出现在坝基上游侧，最小值为-271.00 k Pa.典型截面Ⅰ最大变形值出现在导水墙斜坡顶部，最大变形值为0.045 mm.同时，典型截面Ⅱ的第一主应力最大值出现在下游侧涵洞底部，最大值为85.95 k Pa.典型截面Ⅱ的第三主应力最小值出现在两个涵洞之间的坝体段，最小值为-603.90 k Pa.典型截面Ⅱ最大变形值出现在导水墙斜坡顶部，最大变形值为0.105 mm.

图12 工况2计算云图

计算地震工况采用拟静力法，计算结果云图如图13所示.

图13 工况3计算云图

由图可知，典型截面Ⅰ的第一主应力最大值出现在下游侧涵洞底部，最大值为49.48 kPa.典型截面Ⅰ的第三主应力最小值出现在坝基上游侧，最小值为-287.80 k Pa.典型截面Ⅰ最大变形值出现在导水墙顶部，最大变形值为0.197 mm.同时，典型截面Ⅱ的第一主应力最大值出现在下游侧涵洞底部，最大值为95.21 k Pa.典型截面Ⅱ的第三主应力最小值出现在两个涵洞之间的坝体段，最小值为-582.80 k Pa.典型截面Ⅱ最大变形值出现在导水墙斜坡顶部，最大变形值为0.325 mm.该工况下，结构所产生的变形主要由地震荷载引起.

根据计算结果发现，典型截面Ⅱ的应力值和变形值近似为典型截面Ⅰ的2倍，因此，空心坝在各种工况下运行时，靠近河道岸边的坝段承受更大的应力，同时会产生更大的变形.将3种工况下的计算结果进行对比，可见地震工况为空心坝最危险工况，校核工况其次，正常运行工况最安全.地震工况下坝体应力值与其他两种工况下的坝体应力值差别较小，但变形值近似为其他两种工况变形值的3倍.

4 结 论

本文应用ABAQUS模拟了砌石等效体积单元的基本特性，并对红旗渠空心坝在正常运行工况、校核工况和地震工况下的工作特性进行了三维有限元模拟分析.具体结论如下：

1)浆砌石等效体积单元在Y方向上的极限抗压强度为5.08 MPa，相应峰值应变为3.11×10-4；在Y方向上的极限抗压强度为170 k Pa，相应峰值应变为4.58×10-6；在YZ平面上纯剪的极限强度为1.96 MPa，相应峰值应变为1.90×10-4.

2)在各个工况下，红旗渠空心坝典型截面Ⅰ处第一主应力最大值为49.48 k Pa，第三主应力最小值为-287.80 kPa，最大变形值为0.197 mm；典型截面Ⅱ处第一主应力最大值为95.21 k Pa，最大变形值为0.325 mm，第三主应力最小值为-603.90 kPa.

3)红旗渠空心坝在运行时，其靠近河道左右岸的坝段承受更大的应力，同时会产生更大的变形，因此空心坝的左右岸坝段应视为空心坝主要安全监控坝段.

4)地震荷载主要对坝体变形产生影响.