微通道折叠扁管承压能力仿真分析及优化设计
2019-08-2833
33
(1 上海交通大学制冷与低温工程研究所 上海200240; 2 格朗吉斯铝业(上海)有限公司 上海201800; 3 上海高效冷却系统工程技术研究中心 上海200240)
空调冷凝器的发展经历了管片式冷凝器、管带式冷凝器、平行流式冷凝器三个阶段。平行流式冷凝器采用环保制冷剂,使用的扁管尺寸很小,扁管厚度由管带式冷凝器的毫米级减薄到亚毫米级,属于微通道冷凝器,扁管各流道之间有加强筋,迎风面积相比管片式圆管更小,因此空气侧阻力小,同时扁管管壁厚度更薄。随着汽车空调制冷剂的不断发展,冷凝器也从管带式向平行流式过渡[1]。
微通道管是新一代平行流式微通道空调热交换器的关键零部件,在汽车空调等领域均采用微通道热交换器[2]。微通道产品目前主要有挤压管和折叠管两种形式[3]。挤压管由于技术含量高、生产难度极大,我国铝扁管正向挤压技术发展比较缓慢[4-5]。微通道折叠管由于自身的优异性在空调系统中得到了广泛应用,有着良好的潜力作为挤压管的替代品[6]。
极限承压能力作为评判微通道管性能的重要指标,当时用环保型R134a时,工作载荷达到4.1 MPa,极限承压能力要求达到15 MPa,当使用新型R744时,工作载荷达到15.8 MPa,对微通道管的极限承压能力提出了更高的要求[7]。
H. Miller[8]对钎焊前、后及不同温度下挤压折叠管进行了爆破实验,发现钎焊后挤压微通道扁管极限承压能力下降达17%,随着温度的上升,爆破压力值近似线性下降。方文利等[9]利用K参数法评估挤压扁管焊合质量,进而定性评估挤压扁管的承压性能。唐鼎等[10]利用数值模拟结果,对焊合质量进行评估,并在热模拟实验机上模拟了挤压成形中相应的接触压力和温度下的焊合过程。周宁等[11]基于ABAQUS有限元软件建立了折叠微通道铝扁管压爆实验的有限元分析模型,分析和预测了折叠扁管的承压能力。
目前学者在挤压管方面建立了三维挤压有限元模型,对挤压管的挤压工作原理、耐压性能等方面进行大量研究[12-16],而基于微通道折叠管的性能的研究较少。本文通过对一款折叠管建立ANSYS仿真模型,用实验对比验证结果可靠性。在此仿真模型基础上对折叠管进行优化,提出一种新型内插翅片双片折叠管,并分析不同参数对折叠管极限承压值的影响,得出一款性能优良的微通道折叠管。
1 单片式折叠管的耐压仿真及实验验证
1.1 材料性能
图1所示为微通道折叠管的结构,由多层复合材料经过多道次辊弯成形。多层复合铝合金材料由外侧钎焊层和内侧芯材组成,生产过程中,在材料辊压弯折处于喷涂钎料,可使微通道折叠管一体化成形。

图1 微通道折叠管的结构Fig.1 The structure of microchannel folding pipe
钎焊过程中,钎料层在毛细作用下向钎焊角处流动,冷却后形成钎焊角,芯层也同样经历整个钎焊的热循环过程[11]。钎焊成形图如图2所示。

图2 钎焊成形图Fig.2 The picture of brazing forming
根据单拉实验结果,测得所用铝材的各项性能参数如表1所示。

表1 扁管材料综合材料性能Tab.1 Properties of flat tubular composite materials
图3所示为单拉实验时应力随应变的变化。
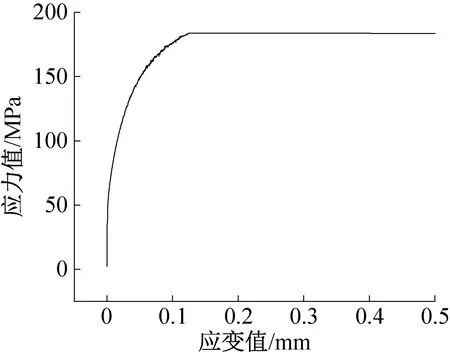
图3 单拉实验时应力随应变的变化Fig.3 The change of stress with strain in single tension test
由图3中实验应力应变曲线标定仿真模型屈服点和失效点,保证仿真材料模型的可靠性。
如果材料中有效塑性应变超过最大等效塑性应变,就会发生故障,即材料发生断裂失效,此时对扁管的外加载荷即其极限承压值。
1.2 模型建立
本文采用ANSYS Explicit dynamics有限元仿真分析软件,可处理模拟短、大变形、大应变、断裂或完全材料故障问题。
显式瞬态动力学分析的运动平衡方程为:

(1)
式中:m为质量矩阵;c为阻尼矩阵;k为刚度矩阵;F(t)为负载向量。
在任何给定时间t,该方程可认为是一组考虑惯性力和阻尼力的静平衡方程。基于一系列线性接近,每个时间步都有多平衡迭代。
从加速度到拉应变动量平衡的偏微分方程:
(2)
(3)
(4)
能量守恒方程:
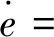
(5)
式中:bx、by、bz分别为x、y、z轴质量体加速度,m/s2;ρ为密度,kg/m3。
为了保证求解的稳定和精确,显式时间积分通过CFL条件加以限制。每个时间步被限制在一个扰动(压力波动)中,不能传递放入比网格最小特征单元尺寸长的时间步。
因此求解稳定的时间步标准为:
(6)
式中:f为稳定时间步因子,1;h为网格特征尺寸,m;c为材料声速,m/s。
建立模型具体尺寸如图4所示,横截面上高度为1.8 mm,宽度为16 mm,所用铝板厚度为0.24 mm,折叠扁管长度为10 mm。

图4 微通道折叠管截面Fig.4 The section size of microchannel folding pipe
根据生产工艺的实际情况,减薄量可以控制在20%以下,此处均采用19.17%的辊弯减薄量。
1.3 仿真实验对比验证
失效分为内泄漏和外泄漏两种。在逐渐增压的情况下,微通道出现应力集中处即辊弯减薄处断裂失效,发生内泄漏,随着压力不断增加,外部管壁断裂出现外泄漏。
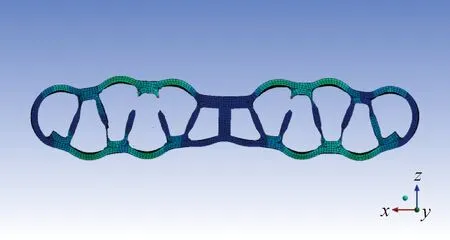
图5 仿真失效图Fig.5 Simulation failure diagram

图6 实验爆破图Fig.6 Experimental blasting drawing
由图5~图6可知,在失效模式上,仿真结果与实验结果拟合较好,辊弯减薄处首先发生断裂失效,随着压力增加,失效进一步发展到外壁面。
表2所示为扁管实验爆破值,经过20组爆破实验可知,该款折叠管的极限承压值平均值为21.9 MPa,与仿真值21.8 MPa十分接近。
考虑实验过程各种非理想状态,如金属成型缺陷导致的极限承压能力下降,爆破实验测量精度影响,可以认为仿真结果反映了真实理论结果,可作为后续仿真的依据。

表2 扁管实验爆破值Tab.2 Experimental blasting value of flat tube
2 内插翅片双片折叠管的仿真模型
从前文仿真分析可知,当承受外加载荷时,失效一般发生在内部肋片辊弯减薄处,而在肋片主体部分外载荷平衡,对外部加压受力不明显。断裂失效的主要原因在于外部管壁受到压力载荷作用弯曲变形对辊弯减薄处产生拉力,因而极限承压能力对外壁壁厚的变化更敏感。
故本文提出一种新型内插翅片式折叠管结构,相同装配尺寸下,当极限承压值不变时,可节省材料,降低生产成本;当使用材料不变时,可极大提高极限承压能力。当制冷剂流通面积相同时,扁管体积更小,使换热器更紧凑。当壁厚减薄时,有利于加强换热。相比于普通微通道扁管,该扁管内片可以实现连续加工,提高生产效率。
2.1 内插翅片式模型建立
在原有折叠板的基础上,本文提出内插翅片式折叠管模型,模型横截面如图7所示。

图7 模型横截面Fig.7 Cross section of the model
该扁管由内外两片复合铝板分别卷制焊接形成,减薄量根据实际情况及前期仿真统一使用减薄19.17%。经过理论分析,外片对极限承压值的影响更大,故外部壁厚大于内部壁厚。
折叠管具体尺寸为:外片壁厚0.2 mm、内片壁厚0.2 mm、横截面长度12 mm、高度为1.4 mm、铝管的长度为10 mm、孔数为19,减薄量为19.17%。
图8所示为在不同压力下,仿真未失效和失效状态。图8(a)中为未失效状态,外片受力较为明显;图8(b)所示为失效状态,此时内插翅片已经失效断裂。

图8 仿真未失效和失效图Fig.8 Simulation non-invalidated and failure diagram
根据理论分析,扁管失效发生在辊弯减薄处,且因为外部壁厚相对较厚,故变形程度较小,经过与理论对比,验证了仿真模型的可靠性。
2.2 仿真分析对比
为了节约成本,提高极限承压能力,加强换热,需了解内片壁厚、外片壁厚、孔数参数的影响权值,故利用仿真模型从这三个角度对折叠扁管的极限承压能力进行分析。
2.2.1 内片壁厚对极限承压值的影响
图9所示为内片壁厚对极限承压值的影响。由图9可知,随着内部壁厚从0.10 mm减至0.08 mm,极限承压能力从30 MPa接近线性减至28 MPa。通过对折叠管参数计算,体积由73 mm3增至79 mm3,相比于初始折叠扁管110 mm3,新型折叠扁管体积减少了28.1%~33.6%,极限承压值增加了21.7%~30.43%。

图9 内片壁厚对极限承压值的影响Fig.9 The influence of inner wall thickness on ultimate bearing value
折叠管的失效集中在辊弯减薄处的断裂失效。随着内片厚度的增加,模型的抗拉强度随之增加,但内片壁厚在增加过程中,增加的壁厚部分被减薄消减,不能完全增加承压值。由图9可知,极限承压值变化较小,对于内片壁厚的变化不敏感。
2.2.2 外片壁厚对极限承压值的影响
图10所示为外片壁厚对极限承压值的影响。由图10可知,随着外片壁厚从0.20 mm减至0.18 mm,极限承压能力从28 MPa接近线性减至23 MPa。通过计算,体积由73 mm3降至68 mm3,相比于初始折叠扁管136 mm3,新型折叠扁管体积减少33.6%~38.1%,极限承压值增加4.3%~30.43%。
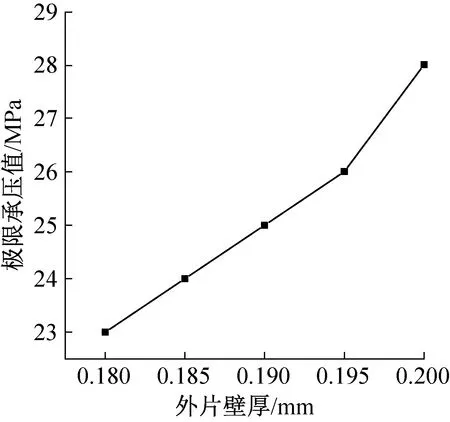
图10 外片壁厚对极限承压值的影响Fig.10 The influence of wall thickness on theultimate bearing value
当载荷不断增加,随着外片壁厚厚度降低,抗变形能力降低,在外片逐渐变形的过程中,对于辊弯减薄处的拉力增大,加快材料的断裂失效,极限承压值也随之降低。因此相比于内片壁厚的变化,极限承压值对外片壁厚的变化较为敏感。
2.2.3 孔数对极限承压值的影响
图11所示为孔数对极限承压值的影响。由图11可知,随着孔数从19增至21,极限承压能力从23 MPa增至33 MPa。

图11 孔数对极限承压值的影响Fig.11 Effect of hole number on ultimateultimate bearing value
随着孔数增加,体积由68 mm3增至71 mm3,使用材料增加,生产工艺成本也增加。当装配尺寸不变时,孔数增加导致内部肋片倾斜度改变,造成焊接焊料形状的改变。综上所述,孔数增加极大提高了折叠扁管的极限承压能力。
2.2.4 最优模型参数选取
选取4款典型参数模型,具体参数如表3所示。通过爆破值来看,模型1、3、4均有优异的性能。模型4极限承压值已经达到33 MPa,但是孔数增加一方面增加耗材,另一方面生产工艺复杂,导致生产效率降低。模型1相比于模型3体积大,耗材多,但是极限承压能力增加不明显。因此模型3的参数最优。

表3 模型参数及极限承压值Tab.3 Model parameters and ultimate pressure values
3 结论
本文通过仿真与实验的对比分析,在原有微通道折叠管基础上对结构进行优化,分析了各参数对极限承压值的影响,得出如下结论:
1)提出该种仿真模型可以较好的模拟折叠管在实际承压时的应力应变情况,可以较好预测新型折叠管的极限承压值,提高设计效率,缩短设计周期。
2)通过仿真不同爆破值结果可知,该内插翅片式折叠管孔数对极限承压值影响最大,其次是外片壁厚,内片壁厚影响最小。
3)优化后内插翅片式折叠管极限承压能力最高可以达到30 MPa以上。相同装配尺寸下,保持极限承压值不变的情况下,可以节省材料,降低生产成本;保持使用材料不变的情况下,可以极大提高极限承压能力。在相同的制冷剂流通面积情况下,扁管体积可以更小,使换热器更加紧凑。
4)基于爆破值-体积参数分析结果可知,孔数、外片壁厚、内片壁厚参数分别为19孔、0.20 mm和0.08 mm时表现优异的极限承压性能。
