基于功能依赖网络分析方法的舰艇战时抢修决策
2019-08-28杨翠蓉周小舟王明哲
窦 帆,杨翠蓉,周小舟,王明哲
(1.华中科技大学 自动化学院,湖北 武汉 430074;2.中国舰船研究设计中心,湖北 武汉 430074)
作为海上作战的重要平台,舰艇能执行防空、反潜、反舰、对地攻击等作战任务,也面临着各种威胁。为保证舰艇能长时间保持有效输出的状态,本文提出受损舰艇的战时抢修[1]。考虑到不同使命任务的舰艇抢修对象不同,时间也是一个重要的约束[2]。功能依赖网络分析(FDNA)是一种能依据系统内部各层级节点之间的功能依赖关系和底层供给节点的效能求得顶层系统效能的方法[3]。
1 抢修后装备性能随时间变化关系
本文研究的主要内容为抢修方案对舰艇效能的影响,目的是找到最优的舰艇战时抢修方案。而抢修方案对舰艇效能的影响需落实到抢修方案对各个受损装备性能的影响。本文中的抢修方案仅考虑时间约束,因此,对于受损装备而言,抢修后的性能是关于时间的函数。采用时间函数f(t)来模拟受损装备性能随抢修时间变化的趋势。f(t)的建立考虑以下几个方面:①受损装备性能的初始值即为装备遭到攻击后的剩余性能;②抢修中,受损装备性能随时间的增长率会受到性能的初始值和结构复杂度的影响:受损装备的剩余性能越大,性能随时间提升越快,结构越复杂,性能随时间提升越慢;③抢修中,受损装备性能的初始值过低,即装备遭到攻击后的剩余性能过低,受损装备无法抢修,仅能维持剩余性能不变,直至遭到下次攻击;④受损装备性能随时间的变化会存在时滞现象,必须经过一定时间的抢修后,性能才能有所提升,而不同装备的时滞时间又存在差异,结构越复杂的时滞时间越长。
基于以上的考虑,本文给出如下描述抢修后受损装备性能随时间变化关系的函数f(t):
f(t)=100(1-μ1e-μ2δ(t-t0)),
(1)
其中:
μ1∈(0,1);
δ∈(0,0.1);
C∈(0,1)。
式中:t为抢修时间,t=0时,f(0)=100(1-μ1),为装备受损后的剩余性能,装备完好时的性能为100 util(util为效能单位);t0为受损装备的必要抢修时间,当抢修时间t≤t0时,受损装备的性能维持剩余性能,没有提升;μ1为装备受损后效能下降百分比;μ2为装备受损程度,μ2=1-μ1,μ2越大,f(t)增长越快;C为装备受损后尚可抢修的临界性能百分比,不同的作战情况下,C值可能会存在差异;当f(0)小于某特定值C时,表示受损装备已经无法抢修,此时f(t)为一条直线,受损装备将维持剩余性能不变,直到下次被击中,f(0)大于等于某特定C值时,抢修能提高受损装备的性能;δ为装备结构复杂度。
2 基于FDNA的效能计算
舰艇的效能与舰艇装备的效能、装备构成的子系统的效能和舰艇、子系统、装备之间的依赖关系相关。本文选择FDNA方法计算舰艇效能。
2.1 FDNA
FDNA是一种可将系统内各个要素之间的依赖关系进行建模和度量的方法,定义了效能接收节点与供给节点之间的依赖强度(SOD)和依赖关键度(COD),给出效能定量化分析计算公式,将其应用于舰艇,得到对应的FDNA模型。
现以单供给、接收节点对的FDNA模型为例,如图1所示。设供给节点的效能为Pi,αij、βij表示供给节点Ni和接收节点Nj之间依赖关系的SOD和COD参数,接收节点Nj的效能Pj为:
Pj=min(SODPj,CODPj),
(2)
其中:
SODPj=αijPi+100(1-αij);
CODPj=Pi+βij;
0≤Pj,Pi≤100;
0≤αij≤1;
0≤βij≤100。
式中:SODPj表示供给节点Ni和接收节点Nj之间依赖关系的SOD,CODPj表示供给节点Ni和接收节点Nj之间依赖关系的COD,接收节点Nj的效能是由SODPj、CODPj之间较小的量决定。
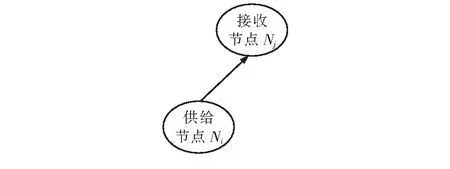
图1 单供给、接收节点对的FDNA模型
当接收节点有多个供给节点时,供给节点和接收节点之间依赖关系的SOD和COD计算如下:
SODPj=avg(SODP1j,SODP2j,…,SODPhj),
(3)
CODPj= min(CODP1j,CODP2j,…,CODPhj),
(4)
式中:SODPj为接收节点Nj与所有单个供给节点Ni(i=1,2,…,h)之间依赖关系的依赖强度SODPij(i=1,2,…,h)的平均值;CODPj为接收节点Nj与所有单个供给节点Ni(i=1,2,…,h)之间依赖关系的依赖关键度CODPij(i=1,2,…,h)中的最小值。
2.2 基于FDNA的舰艇各节点效能计算
基于FDNA给出的计算节点效能的公式,可以依据舰艇底层装备的性能计算得到顶层舰艇的效能。第一层中,共m个装备,令每个装备效能Pi等价于装备性能;第二层中,共n个子系统,每个子系统j抢修前后的效能Pj表达形式相同,为:
Pj=min(SODPj,CODPj),
(5)
第三层为舰艇,同样舰艇z抢修前后的效能Pz的表达形式相同,为:
Pz=min(SODPz,CODPz)。
(6)
3 舰艇抢修模型
3.1 基本假设
1)各类攻击不会使舰艇完全失去作战能力,只是降低作战能力,舰艇仍会保留部分作战能力。
2)舰艇被攻击导致多装备受损后,由于舰艇装载容量有限,可供进行抢修的人力、物力资源紧缺,因此只能进行串行抢修。
3.2 舰艇抢修模型
舰艇抢修的模型为公式(7)~(9):
max(Pz抢修后-Pz抢修前),
(7)
s.t.∑Xi∈Xqti≤T,
(8)
Xq=Xs∩Xtask,
(9)
其中:0≤ti≤T。
式中:Pz抢修前为指定使命任务的受损舰艇抢修前的效能,Pz抢修后为抢修后的效能,Pz抢修后-Pz抢修前为受损舰艇经抢修后总的提升效能;T为当前总的可供抢修的时间;Xs为舰艇受损装备集合,Xtask为作战任务为task的舰艇需要的所有装备集合,其中task∈{对空作战,对陆作战,对海作战},Xq为受损舰艇需要进行抢修的装备;ti为单个需要抢修的受损装备Xi分得的抢修时间。
3.3 模型解法
实际战时抢修中,各受损装备分得的抢修时间不可能无限小。取抢修的最小单位时间Tm为3 min,即抢修时间T每3 min为1份分给各个受损装备,最后剩余小于3 min的抢修时间不再考虑。针对本文目标和数学模型,求解算法流程见图2。可以得到在总抢修时间为T的条件下,能实现舰艇效能增量最大的抢修方案,此方案能适应实际抢修中通常会出现最小单位时间的情形。

图2 舰艇抢修模型求解算法流程图
4 实例分析
现有某使命任务为对空作战的舰艇A在被导弹攻击后,造成声纳装置、垂发装置、舰艇雷达3个装备受损,且各自的剩余性能分别为60 util、40 util、70 util。估计抢修时间T=9 min,现根据本文提出的舰艇抢修模型和解法给出最优的抢修方案,使得受损舰艇抢修前后效能增量最大。
4.1 抢修对象
舰艇A中的受损装备为声纳装置、垂发装置和舰艇雷达,但由于舰艇A的使命任务为对空作战,其中声纳装置不起作用,因此舰艇A待抢修装备就只有垂发装置和舰艇雷达,且各自剩余性能分别为40 util、70 util。根据战时情形,取C为0.3;考虑到受损装备之间结构复杂度的关系为舰艇雷达>垂发装置,于是分别取δ垂发装置=0.07、δ舰艇雷达=0.03,同时取垂发装置、舰艇雷达的必要抢修时间t0为1 min、2.5 min。垂发装置和舰艇雷达对应的抢修后装备性能随时间变化的函数如下:
f(t)垂发装置=100(1-0.6e-0.4×0.07(t-1))
=100-40e-0.028(t-1),
(10)
f(t)舰艇雷达=100(1-0.3e-0.7×0.03(t-2.5))
=100-70e-0.021(t-2.5)。
(11)
4.2 FDNA中参数α、β的获取
目前,FDNA 中的SOD参数α和COD参数β的分析和获取缺乏相关的研究,应用FDNA的文献[5-6]中往往把α和β作为已知条件给出;或者根据系统运行原理、专家经验[7]给出;有学者提出通过体系结构视图模型建立可执行体系结构Petri网模型和体系FDNA模型,进而由Petri网模型仿真得到的出现图(状态转移图)建立体系节点依赖关系矩阵,通过依赖关系进行矩阵的分析和仿真计算[8]。
本文采用专家经验的方式给出相应的α和β参数。图3中将舰艇作战系统、3个子系统和11个装备分为15个节点,按从上往下和从左往右的顺序分别编号为1~15,则存在依赖关系的各节点之间参数α和β如表1所示,其中节点对表示2个存在依赖关系的节点,箭头指向的节点为接收节点,箭头起始的节点为供给节点。

图3 舰艇A作战系统的组织关系图
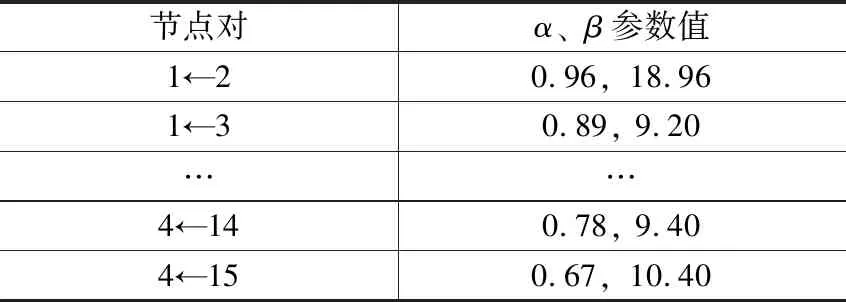
表1 舰艇A作战系统的FDNA模型α和β参数值
4.3 实例模型求解
依据算法,每次在对受损装备进行最小抢修时间3 min的分配评估时,发现舰艇作战系统的效能都是取决于最薄弱的武器系统,且武器系统中仅有垂发装置受损,因此每次的最小抢修时间3 min都分配给武器系统中的垂发装置。经抢修后舰艇作战系统的整体效能由初始的60.6 util增至70.6 util,实现了舰艇作战系统效能的增量最大化。
5 结束语
本文基于给出的抢修后受损装备性能随时间变化的模拟函数,利用FDNA对舰艇系统各节点之间的功能依赖关系进行建模,实现了从装备性能到舰艇系统效能的计算,最终完成了给定使命任务的舰艇在满足时间约束情况下的抢修决策。下一步,应该更多地去了解实际抢修后舰艇上的受损装备性能随时间的变化关系,得到更符合实际的抢修后受损装备性能随时间变化关系的函数,也要寻求能对FDNA方法中表示接收节点Ni和供给节点Nj之间依赖关系的参数α、β定量化计算的方法,更加客观的反应出参数α和β,使本文提出的舰艇战时抢修决策方法在应对实际战时抢修时能给出更加准确的方案。
