对流层映射函数对精密单点定位精度的影响

魏 懂，李浩军

对流层映射函数对精密单点定位精度的影响

魏 懂，李浩军

（同济大学 测绘与地理信息学院，上海 200092）

为了提高对流层延迟的估计精度，进而提高精密单点定位（PPP）的精度，分析不同的对流层映射函数对PPP定位精度的影响：分别采用NIELL、GMF和GPT23种映射函数对IGS测站进行PPP数据处理；并将解算结果与当天IGS的SINEX文件进行比较，分析不同映射函数对测站3个方向定位精度的影响。实验结果表明，方向的定位精度优于方向，采用GMF映射函数的PPP解优于NIELL和GPT2。

对流层延迟；映射函数；精密单点定位；定位精度

0 引言

精密单点定位（precise point positioning, PPP）作为一种全球卫星导航系统（global navigation satellite system, GNSS）定位技术，仅需单台双频GNSS接收机就可以在全球范围内实现高精度定位的技术，其定位精度较高，可达厘米级甚至毫米级。PPP需要综合考虑各种误差改正，其中对流层延迟是影响PPP定位精度较为明显的误差。文献[1]提到当卫星信号经过对流层时，信号因折射产生时延与路径弯曲，形成传播延迟。对流层延迟可以分为由干燥大气引起的干延迟和由大气水汽引起的湿延迟，其中干延迟约占对流层总延迟的90 %，该部分可以通过模型进行较准确的改正。由于大气中水汽含量变化较大，湿延迟难以通过模型精确的改正，需要作为未知参数进行解算。为了准确估计对流层延迟，相关学者作了很多的研究。文献[2]根据全球分布的18个台站共计1 a的高空探测数据建立Hopfield模型，该模型认为大气中的温度梯度值为常数，其模型精度不高，尤其是测站高程较高时，定位精度较低。文献[3]通过连续分式映射函数模型将天顶方向的对流层延迟映射到信号的实际传播方向。文献[4]建立了维也纳映射函数1（Vienna mapping function 1, VMF1）模型，该模型需要获取欧洲中尺度气象预报中心（Europe center for medium-range weather forecasts, ECMWF）的数据，存在数据延迟的问题。文献[5]建立了Saastamoinen模型，使用该模型计算对流层延迟时需要输入测站所在纬度、水汽压、气温气压等参数。后来Collins等人将美国标准大气资料按照纬度进行格网化，提出了UNB3模型。欧洲静地轨道卫星导航重叠服务（European geostationary navigation overlay service, EGNOS）基于UNB3模型建立对流层改正模型，优点是无需输入气象参数，只需要提供年积日、测站高程和纬度就可以根据该模型计算出天顶方向的对流层延迟。

1 PPP数据处理

在PPP数据处理中，采用国际GNSS服务组织（International GNSS Service,IGS）提供的高精度轨道和钟差产品，所求解的参数除了坐标参数，还有对流层延迟、模糊度参数等。本文选择Saastamoinen模型，采用NIELL、GMF和GPT2 3种映射函数对测站进行PPP解算，并将所解算的测站坐标参数与当日IGS的SINEX文件中的坐标进行比较，最后将空间直角坐标转换成站心坐标，比较不同的对流层映射函数对PPP定位精度的影响。

1.1 PPP观测模型

在精密单点定位中，采用的观测量为文献[6]中提到的无电离层组合观测量，即

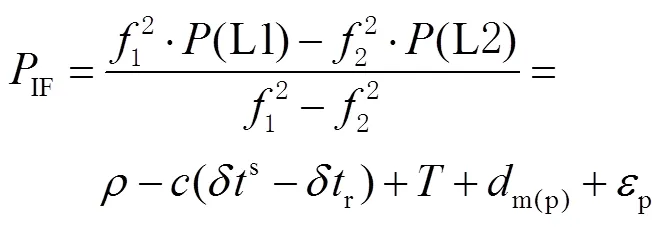
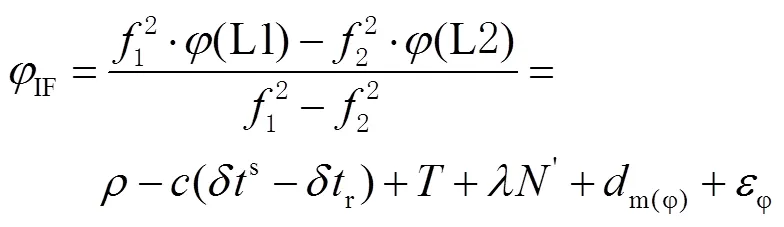
1.2 对流层延迟解算模型

对流层延迟一般可分为干延迟和湿延迟2部分，干延迟约占总延迟的90 %，湿延迟约占10 %，且对流层延迟一般与气温、气压、湿度等关系密切[7]。通常，信号的传播方向不是在天顶方向，因此需要将天顶方向对流层延迟映射到信号实际的传播方向。文献[8]中指出，此时该方向的对流层延迟可以表示为天顶干延迟、湿延迟与干映射和湿映射的乘积之和，公式为

本文选择Saastamoinen模型，文献[9]提出该模型中将对流层分成2部分：第一层是地表到对流层顶部，其气体温度递减率为常数，假设为6.5℃/km；第二层为对流层顶部到平流层顶部，大气温度保持不变，假设为常数。

天顶方向对流层延迟可表示为

1.3 对流层映射函数

天顶延迟与映射函数的组合才可以获得斜路径延迟，因此映射函数的准确性影响着斜路径延迟的精度，进而影响到精密单点定位精度。因此选择合适的对流层映射函数对PPP的定位精度具有重要的作用。本文选择NIELL、GMF和GPT2 3种映射函数进行PPP解算。

1.3.1 NIELL映射函数

文献[10-11]指出NIELL模型是由Niell根据分布全球的26个探空气球站的观测数据建立的一种典型的经验模型，该模型考虑到测站所在纬度、高程、观测时间和对流层季节性变化性等因素，未考虑气象参数（气压、水汽压和温度等）可能对模型产生的影响。NIELL映射函数表示如下：

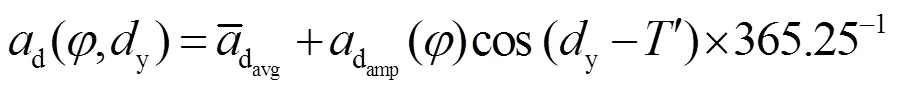
表1 NIELL模型干分量系数

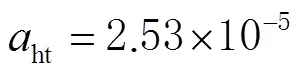
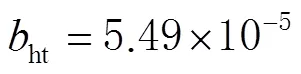
表2 NIELL模型湿分量系数

1.3.2 GMF映射函数

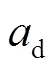
1.3.3 GPT2映射函数

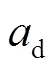
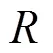
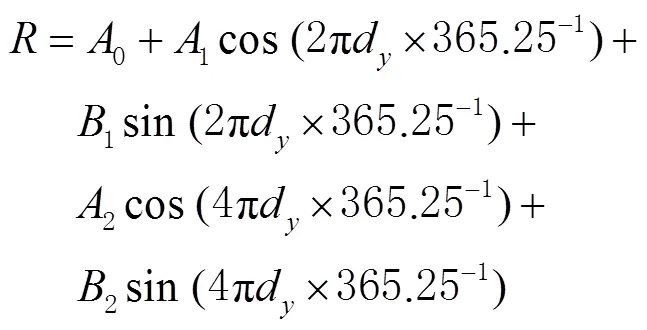
2 实验与结果分析

本文选取GLSV、LCK4、MATE、NIST、SULP和SUMK共计6个IGS站，采用2018年7月20日的观测数据，对流层模型选择Saastamoinen模型，分别使用NIELL、GMF和GPT2映射函数进行PPP解算，然后利用IGS提供的当天的SINEX文件，将空间直角坐标（，，） 转换为站心坐标（，，），对比不同映射函数所解算的、、方向定位结果，分析不同的对流层映射函数对精密单点定位精度的影响。具体结果如表3所示。

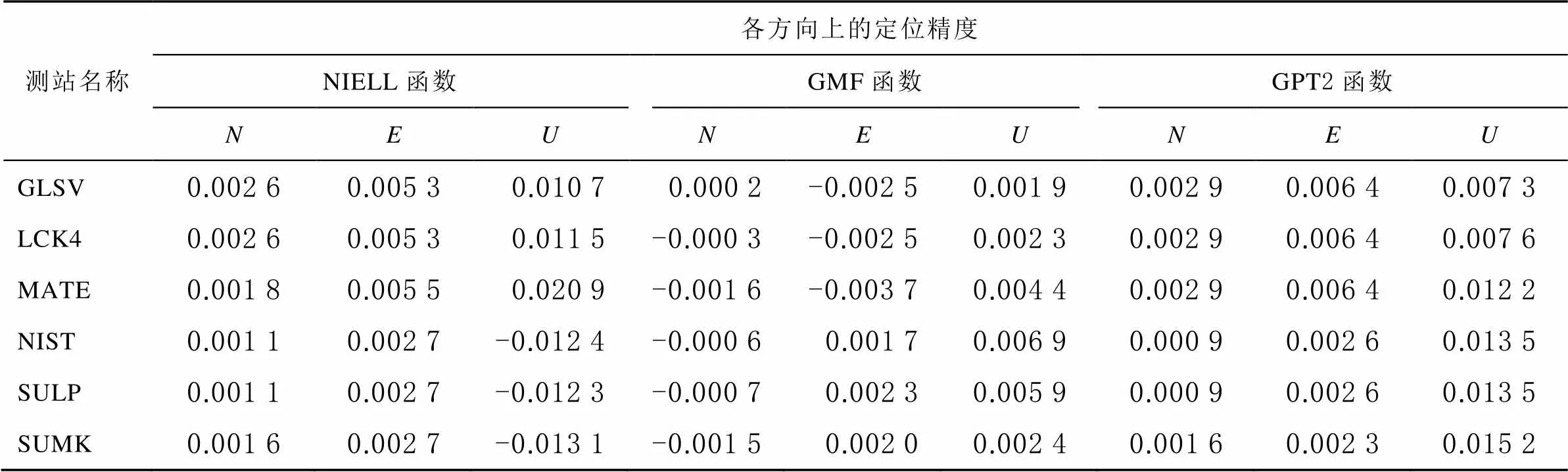
表3 测站的位置参数与SINEX文件的比较 　　 m

图1至图3为各个测站采用3种映射函数在3个方向上的定位结果。

图1 测站N方向定位结果比较

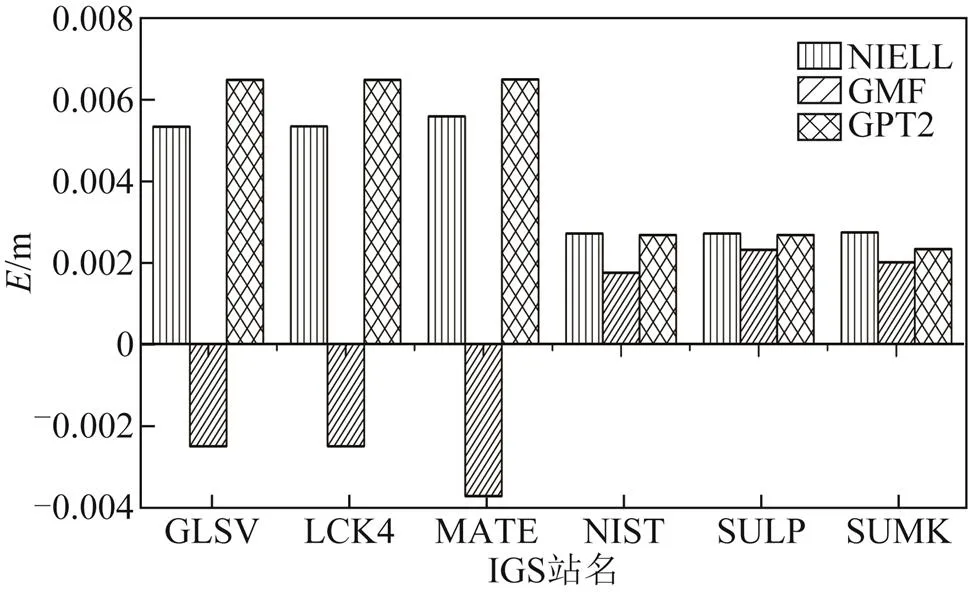
图2 测站E方向定位结果比较

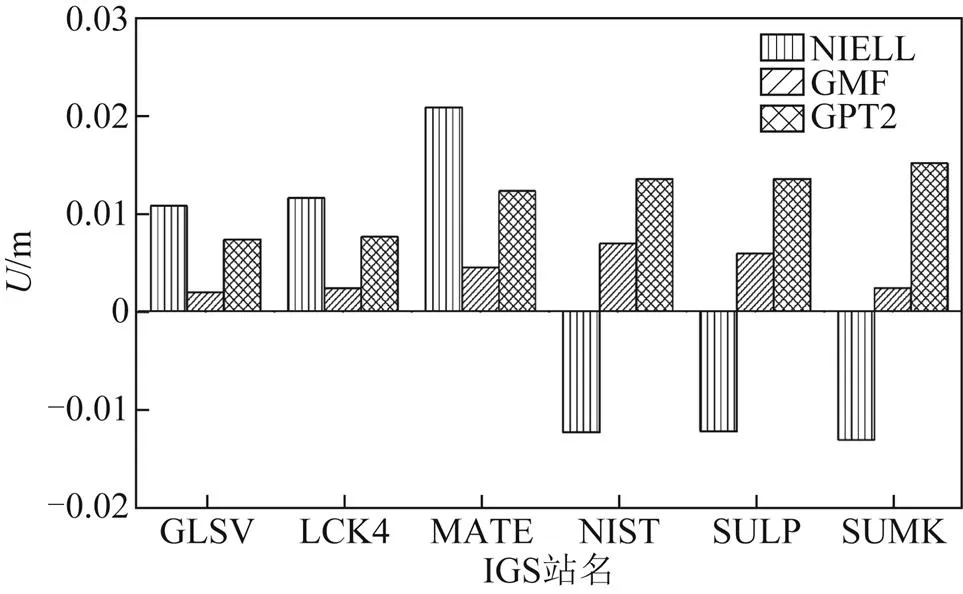
图3 测站U方向定位结果比较

采用NIELL、GMF和GPT2映射函数的各测站在方向的均方根值（root mean square, RMS）如表4所示。

表4 不同映射函数下N、E、U方向的RMS 　　mm

3 结束语

本文介绍了3种对流层映射函数（NIELL、GMF和GPT2），通过对IGS测站进行PPP解算，比较分析不同的映射函数对精密单点定位精度的影响。通过数据处理可以得出如下结论：

1）在方向上，NIELL、GMF和GPT2 3种映射函数所解算出来的结果与IGS的SINEX文件提供的坐标差值均在1 cm以内；方向最大值在4 mm以内；方向最大不超过8 mm；RMS均在5 mm以内。整体上看，方向定位精度优于方向，且采用GMF映射函数的PPP解精度最高，NIELL次之，最后是GPT2模型。

2） 在方向，3种映射函数所解算的坐标差值不大于2.5 cm，但是坐标差值普遍大于方向的差值。采用NIELL和GPT2映射函数的均方根值大于10 mm，而采用GMF模型的解优于其他2种，定位精度相对较好。综合各个测站表明，方向上的定位精度弱于方向。3种对流层映射函数中，GMF相对较好，定位精度高于其他2种映射函数。

[1] 李盼,李星星, 王磊, 等. 对流层湿延迟估计方法对PPP数据处理的影响[J]．武汉大学学报(信息科学版), 2010, 35(7): 850-853.

[2] HOPFIELD H S. Two-quartic tropospheric refractivity profile for correcting satellite data[J]. Journal of Geophysical Research, 1969, 74(18): 4487-4499.

[3] MARINI J W. Correction of satellite tracking data for an arbitrary tropospheric profile[J]. Radio Science, 1972, 7(2) : 223-231．

[4] BOEHM J, SCHUH H. Vienna mapping functions in VLBI analyses[J]. Geophysical Research Letters, 2004, 31(1)：277-281.

[5] SAASTAMOINEN J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites[J]. The Use of Artificial Satellites for Geodesy, 1972: 247-251.

[6] ZUMBERGE J F，HEFLIN M B, JEFFERSON D C，et al. Precise point positioning for the efficient and robust analysis of GPS data from largr networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017.

[7] 翟树峰. GNSS对流层延迟改正及其应用研究[D]. 郑州：信息工程大学, 2018: 14-15.

[8] 施展, 孟祥广, 郭际明, 等. GPS精密单点定位中对流层延迟模型改正法与参数估计法的比较[J]. 测绘通报, 2009( 6): 9-11.

[9] 殷海涛, 黄丁发, 熊永良, 等. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报(信息科学版), 2007, 32(5): 454-457.

[10] 翟树峰, 吕志平, 崔阳, 等. 对流层映射函数对精密单点定位的影响分析[J]. 测绘工程, 2018, 27(1): 24-30.

[11] 李黎, 匡翠林, 朱建军, 等. 水平梯度和映射函数对PPP对流层延迟估计的影响分析[J]. 工程勘察, 2011(5): 52-56.

[12] 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武大出版社, 2010: 64-70.

[13] BOEHM J, NIELL A, TREGONING P, et al. Global mapping function(GMF): a new empirical mapping function based on numerical weather model data[J]. Geophysical Research Letters, 2006, 33(7): 199-208.

[14] 王君刚, 陈俊平, 王解先. GNSS对流层延迟映射模型分析[J]. 天文学进展, 2014, 32(3): 383-394.

[15] 徐杰, 孟黎, 任超, 等. 对流层延迟改正中投影函数的研究[J]. 大地测量与地球动力学, 2008, 28(5): 120-124.

[16] 郭际明, 章迪, 史俊波, 等. 利用射线追踪法分析三种典型对流层映射函数在中国区域的精度[J]. 武汉大学学报(信息科学版), 2015, 40(2): 182-187.

[17] 姚宜斌, 曹娜, 许超钤, 等. GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726-733.

Influence of tropospheric mapping function on precise point positioning accuracy

WEI Dong，LI Haojun

（College of Surveying and Geoinformatics, Tongji University, Shanghai 200092, China）

In order to improve the estimation accuracy of tropospheric delay, and further improve the accuracy of precise point positioning (PPP), the paper analyzed the influence of different tropospheric mapping functions on PPP accuracy: the three mapping functions of NIELL, GMF and GPT2 were used to conduct PPP data processing for IGS observation station, and the calculation result was compared with IGS SINEX file of the day to analyze the influence of the functions on the positioning accuracy in the three directions of,andExperimental result showed that the positioning accuracy of the directions ofandwould be better than that of, and the PPP solution with the adoption of GMF mapping function would be better than that with NIELL and GPT2.

tropospheric delay; mapping function; precise point positioning; positioning accuracy

P228

A

2095-4999(2019)03-0082-05

2018-11-08

国家自然科学基金项目（41674029）。

魏懂（1994—），男，江苏徐州人，硕士生，研究方向为大地测量学与测量工程。

李浩军（1981—），男，甘肃平凉人，博士，副教授，研究方向为大地测量学与测量工程。

魏懂，李浩军.对流层映射函数对精密单点定位精度的影响[J].导航定位学报,2019,7(3):82-86.（WEI Dong，LI Haojun.Influence of tropospheric mapping function on precise point positioning accuracy[J].Journal of Navigation and Positioning,2019,7(3):82-86.）

10.16547/j.cnki.10-1096.20190314.