以“学为中心”课堂中小学生高阶思维能力的培养

江燕美

摘要：高阶思维作为一种较高水平的思维，正逐步被人们所了解和重视。和其他思维一样，高阶思维是可以培养和传授的，以学为中心的课堂教学是培养高阶思维最有效的途径。本文结合外出学习与教学实践，提出在学生原有认知上，学生问题解决过程中，学生活动探究里三条策略指向高阶思维，进而培养学生的高阶思维。

关键词：高阶思维;以学为中心

数学教学的核心是培养思维能力。美国教育家布卢姆将思维能力按由低到高细化为六个水平：记忆、理解、应用、分析、评价、创造，其中，前三者是低阶思维，具体表现为机械性的识记或完成简单的任务;而高阶思维是发生在较高认知水平层次上的认知能力，其核心表现为分析能力、批判性思维能力和创新能力。纵观当前的小学数学教学，教师往往更注重让学生听得懂，学的会，掌握熟练，也就是说教师们更注重学生的低阶思维，而忽视对学生高阶思维能力的培养。然而走出校门，这些学科知识中的简单记忆、理解和知识运用终将逐渐被遗忘，唯有高阶思维才能转化为人们终身受益的能力。那么，如何在学科教学中指向高阶思维能力的培养呢？课堂是教学的主阵地，“以学为中心”是当下课堂教学的追求，以学生为本，培养学生的学习力，促进学生发展为主线，通过课堂教学的叠加，助推学生的学科核心素养的形成、提高与发展。本人借此机会，结合外出学习与教学实践来谈谈基于“学为中心”课堂中高阶思维能力的培养策略。

1 基于学生原有认知上的高阶思维的锻炼

奥苏贝尔就曾指出：影响学习最重要的因素是学生已经知道了什么。而学习的过程，不过是将新知识不断同化到已有认知结构的过程。以学生原认知为基础，以知识的生长点为切入口，沟通数学知识与学生原认知间，数学知识与知识间的关联，让学生数学思维“结构化”，让零散的知识串成结构化、系统化的知识整体，使学生学习呈现一种树状的生长态势。

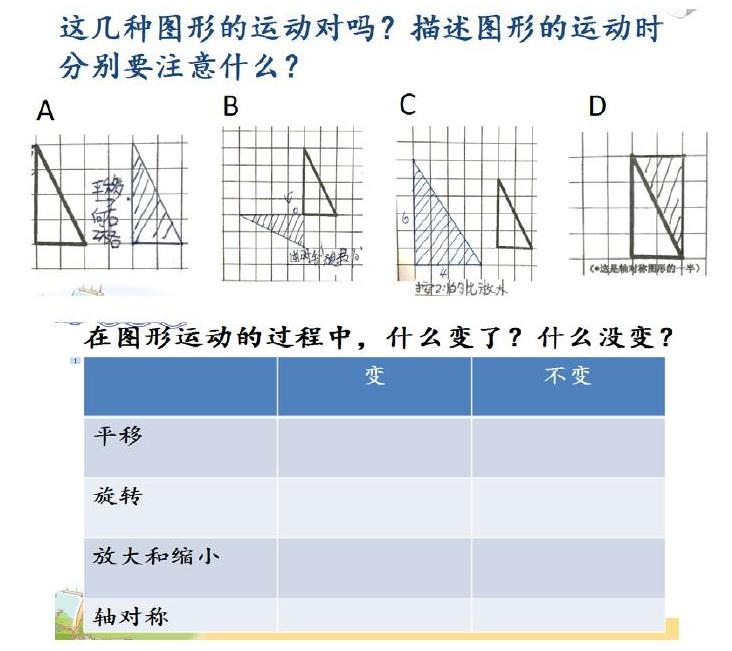
比如，六年级下册总复习的《图形的运动》，将四种图形的运动集中在一起一节课。教师以学习单中三角形的运动为例，将学生的整理和复习的工作前置，课堂上用小组交流，学生汇报的形式自主整理，暴露学生知识的易错点和盲点，在师生、生生互动中学生自觉的发现并描述各种运动时需要注意的地方。知识的重温是不可缺少的，但或仅限于此，还只是停留在熟练掌握的低阶思维的水平。教师在学生原有认识的基础上，进一步引导学生找到知识的的联系点，让学生观察思考，不同的图形运动，变化后的图形与原来图形相比较，它们什么变了，什么没有变？这四种图形运动后的形状都不变，但这些不变中又有什么不同呢？为什么说它们的形状不变呢？在“变”与“不变”中，学生深刻认识到：原来这些图形的运动都是有联系的，体会图形刚性运动和相似变换的特点。

比如教学《直线、射线、线段》，普遍教法是：教师借助实物图片和空间想象，让学生直观感受直线、射线、线段的图形特征，然后引导学生画出图形，结合图形辨析三者的区别和联系。其实，这种教学关注点是知识点，缺乏数学内在逻辑的思考，学生的思维不够深入和连贯。笔者在教学中，研究和梳理知识的内在结构，做了这样的教学尝试：地图上的2个城市可以看成2个点，连接2个点之间的路径叫做线。线有曲直之分。在平面上画2个点，用字母表示它们，并用线段连接它们。接着以线段为基础，延伸到直线和射线的认知。在教学中有意调整了线段、直线、射线的序，从线段的认识入手，以线段为知识的起点，借助想象理解直线和射线的“无限延伸”，采用从整体到部分的逆向提问方式“线段、射线、直线有什么联系？给你第一条直线，能得到线段和射线吗？说明它们之间有什么联系”。抓住知识的数学本质，理清内容本身的逻辑关系，把握知识形成的核心思维，着眼于数学知识的整体，着眼于数学知识的关联，让学生真正做到学有所悟。

以上两个例子，执教者在学生原认知的基础上，那问题走深、走广，从低阶思维走向高阶思维，进而发展学生的分析解决能力。

2 基于学生问题解决中的高阶思维的提炼

激活学生的思维离不开教师的引导。学生学习就是面对一个个未知的问题，解决问题的过程中，教师要安排好教学的序，进行适当的教学干预，引导学生的思维方向，让学生洞察数学知识的本质。学生在层层递进的教学素材中开展积极的思考和探究，进而发展高阶思维。

比如，特级教师俞正强老师执教的《体积与容积》。体积、容积的概念一线教师往往是从抽象的角度认识，尽管学生也能准确复述出书本中的概念，但学生的空间观念却没有得到发展。针对这样的现状，俞老师从“空间”入手，学生一开始只能从一些理论上进行描述，俞老师就让学生从生活中找空间，用具体的事物，让孩子明白物体在空间里，借助两位一胖一瘦的同学，比较他们空间的大小。能用形象直观的语言表达抽象的概念，才算对概念的真理解。最后，体积和容积有联系也有区别，俞老师特别巧妙的利用“套娃”这一选材，一层一层打开，让学生们找“套娃”中的规律，原来大娃的容积就是2娃的体积，因为大娃可以装下2娃，而7娃呢？7娃没有容积，只有体积。在立序上，俞老师也做了精心的设计，从空间概念，体积容积的概念，再到空间组成（平面与空间），步步引导，以铅笔盒为例，在学生的描述中，充分理解空间和平面的管理，原来空间是用平面围城的。

比如，在《圆的认识》中，教学目标要解决圆的概念和圆的特征等问题，如何在教学中培养学生的高阶思维呢？教师设计了“我尝试”，“我探究”，“我设计”三个层次的序。从尝试用圆规画圆，体会如何才能画好一个圆。到探究同一个圆内半径和直径间的关系。渗透用极限的思想，从正四边形，正六边形，正八边形，正十三边形，让学生体会圆处于矩的道理。最后，学以致用，用圆的知识设计一个套圈游戏的公平规则。在教学环节中围绕是什么，为什么，怎么用的认知过程，引导学生经历自主学习，合作交流，知识再创造，在“让—以学生为中心”和“引—教师的引导”之间不留痕迹的是学生的数学思维得到发展。

3 基于学生活动探究里的高阶思维的培养

数学思维是数学化的的特质，在探究活动中，教师引导经历从现实问题抽象成数学问题的横向数学化过程，再到对数学问题进行提炼和概括纵向数学化过程。当学生不仅能依靠记忆，还能运用抽象，推理，建模解决问题时，其高阶思维能力也悄然生成。

比如，特级教师朱国荣执教的《自行车里的数学》，就将一辆真实的自行车带进课堂。用大问题串的方式“自行车里有什么值得研究的数学问题呢？单车和私家车有什么不同呢？变速车你认为有怎么组合最快、最慢，说出你的理由？”将学生自身于真实的问题情境中，学生发现可以研究车轮的周长，面积，甚至自行车的重量等等，经过师生的筛选，共同制定本节课有价值、可研究的问题：自行车蹬一圈能走多远呢？如果蹬同样的圈数，变速自行车的哪一种组合可以走的更远呢？在真实有意义的情境中，才能最大程度的激发学生学习的意愿，实现横向化的数学过程。本课所涉及的自行车传动的原理，朱老师教师通过观察和演示让学生明白，如：前轮，后轮，前齿轮，后齿轮在哪里？自行车是依靠哪个轮子前进的？后轮又是依靠什么动起来的呢？等等。在观察自行车的运动过程中，让学生思考：在链条传动的过程中，存在怎样的等量关系？解决问题的关键是求后轮的圈数。以真实的研究为背景，学生的已经经验被唤醒，在情境中主动进行抽象、分析、概括的探究活动，引發自身的高阶思维。

比如，在教学《平时四边形的面积》时，学生在“画—剪—移—拼”的方法寻找平行四边形的面积公式。当学生真正深度理解并掌握如何用转化的方法求解平行四边形的面积公式后，自然会调动联想，从而推导出三角形、梯形、圆的面积公式。同样的道理，有面到体，学生也能通过联想，实现认识上的再一次飞跃。

总之，学生数学高阶思维的发展是学生数学核心素养生成的重要标识。在数学教学中，教师要探明学生思维的生长点，开阔学生的认识视角，引爆学生的思维的可燃点，促进学生从低阶思维迈向高阶思维。

基金项目：本文系福建省教育科学“十三五”规划“名师科研成果在区域小学数学教学中深化研究”（编号：FJJKXB17-478）阶段研究成果。

（作者单位：福州市仓山区实验小学）