联合水汽因子的GA-BP神经网络PM2.5质量浓度预测

刘林波,刘立龙,黎峻宇,黄良珂,周 威,甘祥前

(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006)

0 引 言

近年来,我国多个城市(北京、 天津、 西安等)不断发生大规模的雾霾灾害天气,现已成为制约我国区域经济发展和影响城市环境的热点问题[1]。产生雾霾的主要原因是空气污染和一些气象因素的共同作用[2],在组成雾霾的众多污染物中,最具有局域性特征、对人体危害最严重的污染物为大气中细颗粒物PM2.5,其可以作为反映雾霾灾害严重程度的一个指标。研究表明,雾霾灾害的成因与CO、NO2、SO2、O3等大气环境因子和湿度、温度、风速等气象因子密切相关[3-5]。随着GPS气象学的发展,文献[6]利用2016年北京市GPS-PWV(GPS-Precipitable Water Vapor)数据与PM2.5质量浓度进行比较,发现两者存在着明显的正相关性。文献[7-8]研究表明,GPS-PWV是影响雾霾天气的一个重要因素,可将其作为预测雾霾的一个关键参数。

针对雾霾与诸多大气环境和气象因子密切相关的这一特性, 国内外许多气象学者们都在研究建立科学、 准确、 实时的雾霾预测方法。 由于人工神经网络方法可以解决预测数据的非线性和强突变特征等问题, 因此将其作为预测雾霾严重程度的主要方法[9-11]。但是, 使用单一的BP神经网络模型预测的输出结果误差较大[12], 且容易突变,不能满足实际雾霾预测的要求。 为解决这些重要问题, 本文采用了GA-BP神经网络模型进行预测。 遗传算法[13]是一种全局优化搜索算法, 可对BP神经网络的初始权值和阈值进行优化选择,能够避开局部极小点,克服BP神经网络的缺点,两者的结合使得模型具有更高的稳定性和预测精度。

基于以上研究, 本文通过对比分析北京市2015年第275～280天3个陆态网络(crustal movement observation network of China,CMONOC)站点的GPS-PWV数据以及影响雾霾的其他大气环境数据、气象数据与PM2.5质量浓度数据之间的相关程度,利用GPS-PWV数据联合相关性较强的影响因素作为预报因子,采用GA-BP神经网络模型进行PM2.5质量浓度预测,并将其与BP神经网络模型的预测值进行精度对比,分析引入GPS-PWV因子能否提高PM2.5数据的预测精度。

1 主要影响因素分析与选取

本实验采用了CMONOC基准站数据和NOAA气象站的相关气象数据, 通过萨斯塔莫宁(Saastamoinen, SA)模型联合反演求取北京市2015年第275～280天雾霾严重时期3个CMONOC基准站点(BJFS、BJGB、BJSH)天顶方向的GPS-PWV值。

SA天顶静力学延迟计算模型为

(1)

式中:ZHD为对流层天顶静力学延迟, mm;PS为地面气压, hPa;θ指的是观测站的大地纬度, °;H为测站的大地高, km。利用下载CMONOC基准站数据中对流层天顶总延迟(ZTD)减去ZHD即得到对流层湿延迟(ZWD), 则大气水汽总量(PWV)可表示为

(2)

式中:K代表转换系数;ρw表示水的密度;Rv表示水汽气体常数;k2′、k3为大气折射常数;Tm表示大气加权平均温度, K。

通过中国空气质量在线监测分析平台(http://www.aqistudy.cn/)下载得到2015年第275～280天北京市的CO、NO2、SO2、 O3、 PM2.5等大气环境数据及湿度、 温度、 风速等气象数据, 这8组数据时间分辨率均为1 h, 每组共144个样本值。 各影响因素与PM2.5之间的时间序列关系见图1。

可知,在北京市2015年第275～280天, 3个CMONOC站的GPS-PWV以及NO2、 CO含量分别与PM2.5质量浓度数据在时间序列的变化下具有很好的对应关系, 各影响因素的上升、 下降过程对应了PM2.5质量浓度数据的上升下降过程, 这种现象尤其明显地表现在各数据曲线的峰顶和低谷处。 而SO2、O3、 风速、 温度、 湿度与PM2.5质量浓度数据在时间序列的变化下的对应关系并不是特别明显。 为进一步分析各因素与PM2.5之间的关系, 本文采用相关性分析方法[14]表征其相关程度, BJFS站GPS-PWV、 BJGB站GPS-PWV、 BJSH站GPS-PWV、 NO2、 SO2、 CO、O3、风速、温度、湿度等影响因素与PM2.5质量浓度的相关系数分别是0.642 2、 0.644 1、 0.641 3、 0.648 7、0.348 5、0.958 4、0.364 1、-0.248 4、0.198 4和0.451 1。

结合图1可知:北京市3个站点的GPS-PWV与PM2.5质量浓度在时间序列的变化下具有很好的对应关系,总体呈中度相关,因此由GPS反演的GPS-PWV可以作为本次预测PM2.5质量浓度的一个重要参数。NO2、SO2、O3、湿度与PM2.5之间的也具有很好的相关性,属中度相关。CO与PM2.5之间的相关系数更是达到了0.958 4,属高度相关。从整体上看,风速和温度在该时段与PM2.5数据的相关性较小,属低度相关。

由雾霾的成因分析可知,影响雾霾程度的因素很多,通过分析各个影响因素与PM2.5之间的相关性,合理地选取影响雾霾程度的主要预报因子,剔除相关性较弱的预报因子,从而避免预报的冗余度,这对于提高PM2.5预测的精度至关重要,进一步说明了本文工作的必要性。为保障GA-BP神经网络预测PM2.5质量浓度的精度,本文选取了CO、NO2、SO2、O3、湿度以及GPS-PWV数据作为预报因子,以提高其预测精度。

2 GA-BP神经网络模型的建立

BP神经网络是近年来应用广泛的一种多层前馈神经网络,其采用信号前向传递,误差反向传播的方法,并以均方根误差最小化为目标调整网络权值和阈值。这种学习方法解决了多层前馈神经网络的权重调整问题,使得最终预测值不断逼近真实值。但在实际使用BP神经网络预测过程中发现其存在着隐含层神经元个数的最佳值没有定论、初始权值和阈值是随机产生、容易陷入局部极值等问题[15]。

图1 各影响因素与PM2.5质量浓度对比Fig.1 Comparison of influencing factors and concentration of PM2.5

遗传算法是一种模拟自然界遗传机制和生物进化论的并行随机搜索最优化方法,具有良好的全局搜索性能,不易陷入局部极小等优点。遗传算法能够优化BP神经网络的初始权值和阈值,且适用于并行处理,搜索不依赖于梯度信息,可以用来优化BP神经网络[16]。遗传算法优化BP神经网络的公式为[17]

(3)

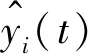
(4)

GA-BP模型预测PM2.5质量浓度可分为BP预测模型结构确定、遗传算法优化BP预测模型和预测3部分。BP神经网络结构可由拟合函数输入输出参数的个数确定,进而确定遗传算法个体的长度。遗传算法可优化BP神经网络的权值和阈值,可通过选择、交叉和变异操作找到最优适应度值对应的个体。BP神经网络预测是将遗传算法得到的最优个体对网络初始权值和阈值赋值,网络经训练后预测输出。

经分析可知:在本文试验中,当不含水汽影响因子时,其输入参数5个、输出参数1个,所以设置的GA-BP神经网络输入层有5个节点,隐含层有5个节点(单隐层),输出层有1个节点,共有5×5+5×1=30个权值,5+1=6个阈值,在遗传算法中采用实数法对个体进行编码,其长度为30+6=36;当含水汽影响因子时,其输入参数6个,输出参数1个,所以设置的GA-BP神经网络输入层有6个节点,隐含层有6个节点,输出层有1个节点,共有6×6+6×1=42个权值,6+1=7个阈值,遗传算法个体编码长度为42+7=49。本次实验选择北京市2015年第275～280天雾霾严重时期的144组数据,前120组(275～279天)数据作为神经网络训练样本,后24组(280天)作为预测样本。遗传算法的参数设置为:进化次数为1 000,种群规模为10,变异概率为0.2,交叉概率为0.4。其GA-BP神经网络模型通过MATLAB R2014a软件进行编程实现。

GA-BP模型预测PM2.5质量浓度网络算法流程见图2。

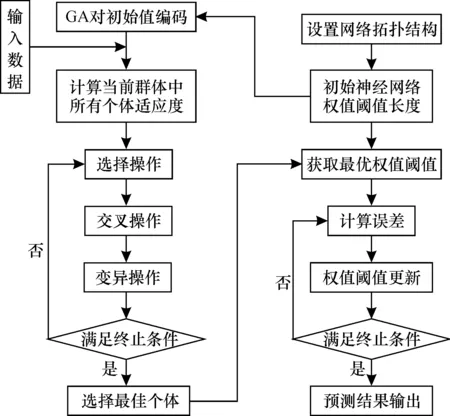
图2 GA-BP神经网络预测PM2.5质量浓度流程图Fig.2 Prediction of PM2.5 mass concentration flow chart by GA-BP neural network

3 实验结果分析

本文利用北京市2015年第275～279天120 h的PM2.5数据作为样本,分别通过GA-BP神经网络模型和BP神经网络模型预测第280天24 h的PM2.5值,其中不含水汽预测值指将CO、NO2、SO2、O3、湿度作为输入因子的预测结果,含水汽预测值则是分别增加了各CMONOC 站点(BJFS、 BJGB、 BJSH)的GPS-PWV数据作为输入因子的预测结果,分别如图3、图4所示。

图3 2015年第280天24 h实测PM2.5含量和BP神经网络预测PM2.5含量对比Fig.3 Comparison of measured PM2.5 content and BP neural network prediction of PM2.5 content on 280th day and 24 hours in 2015

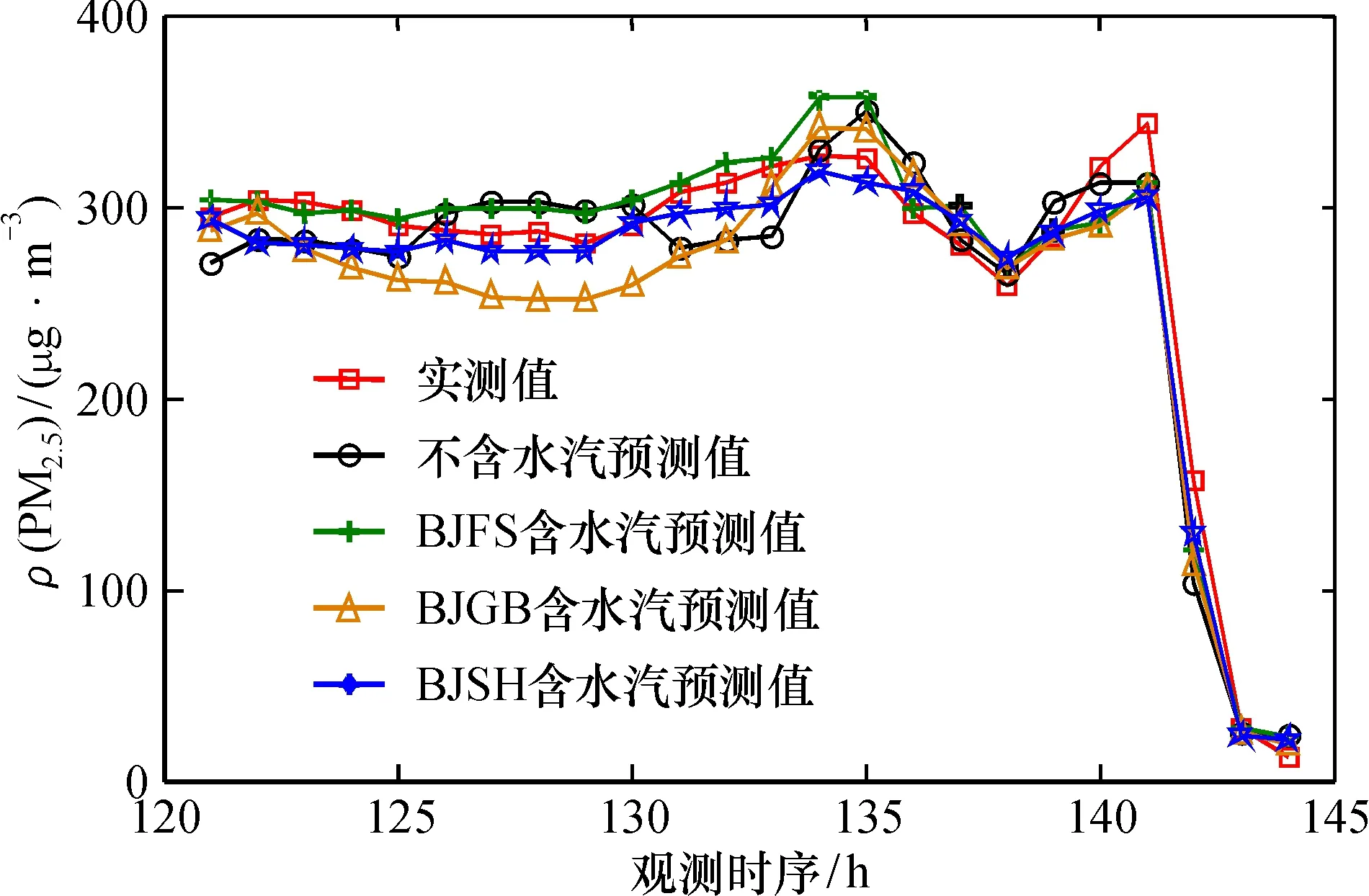
图4 2015年第280天24 h实测PM2.5含量和GA-BP神经网络预测PM2.5含量对比Fig.4 Comparison of measured PM2.5 content and GA-BP neural network prediction of PM2.5 content on 280th days and 24 hours in 2015

预测因素BPBiasRMSEGA-BPBiasRMSE不含GPS-PWV35.823.737.334.6BJFS含GPS-PWV41.330.145.540.8BJGB含GPS-PWV18.812.820.313.2BJSH含GPS-PWV22.216.823.416.0

综合可知,BP神经网络模型预测值的Bias 和RMSE均远远大于GA-BP神经网络模型预测值。通过对比分析两种模型的预测值可以看出:在预报因子不同的条件下,使用GA-BP神经网络模型预测的数据精度更高,数据稳定性更好,可以预测出接近实际的PM2.5数据。因此,本文将着重对GA-BP神经网络模型的预测值作出详细分析。

在GA-BP神经网络中,BJFS和BJSH站点的GPS-PWV数据联合其他主要影响因素作为预报因子的预测值,其Bias和RMSE均小于不含GPS-PWV时的预测值,而含BJGB站点GPS-PWV预测值的Bias和RMSE分别为20.3、23.4,大于不含GPS-PWV时的18.8和22.2。这种情况是由于各站的高程不同引起的,3个CMONOC站BJFS、BJGB、BJSH的海拔高为87.5、213.0、155.4 m,均高于北京市的平均海拔55.0 m,BJGB站与北京市的海拔差值最大,达到158 m。随着测站海拔与北京市的海拔高度差值增大,当大于64 m后,PM2.5质量浓度会表现出随高度增加而递减的趋势,因此对于BJGB站点的预测值影响更加明显,使得预测值精度相对有所降低。

为进一步比较不同预报因子GA-BP神经网络预测值的优劣,利用各预测值的相对误差来进行精度分析,使其能更好地反映预测值的可靠程度。其中,相对误差=(|真实值-预测值|/真实值)100/%,相对误差越小,预测精度越高。不同预报因子的预测值相对误差见图5。

在预报因子不同的4种情况下,总体上模型预测的结果与真实监测值前21 h预测值相对误差均在10%左右。在22:00—24:00,4种情况下的预测值相对误差均产生极大变动,尤其是在预测因子不含GPS-PWV的情况下的预测值相对误差变化最为明显。产生这种情况是由于风速的快速变化,北京市在2015年第280天22:00时风速3级,随后在接下来的1 h内迅速增加到7级,最终24:00时达到8级。随着风速的增加,大气中的PM2.5微颗粒物被吹散,PM2.5数值由21:00的343 μg/m3急速降到24:00的12 μg/m3。为更好地描述不同预报因子的预测误差,将相对误差详细情况列于表2。

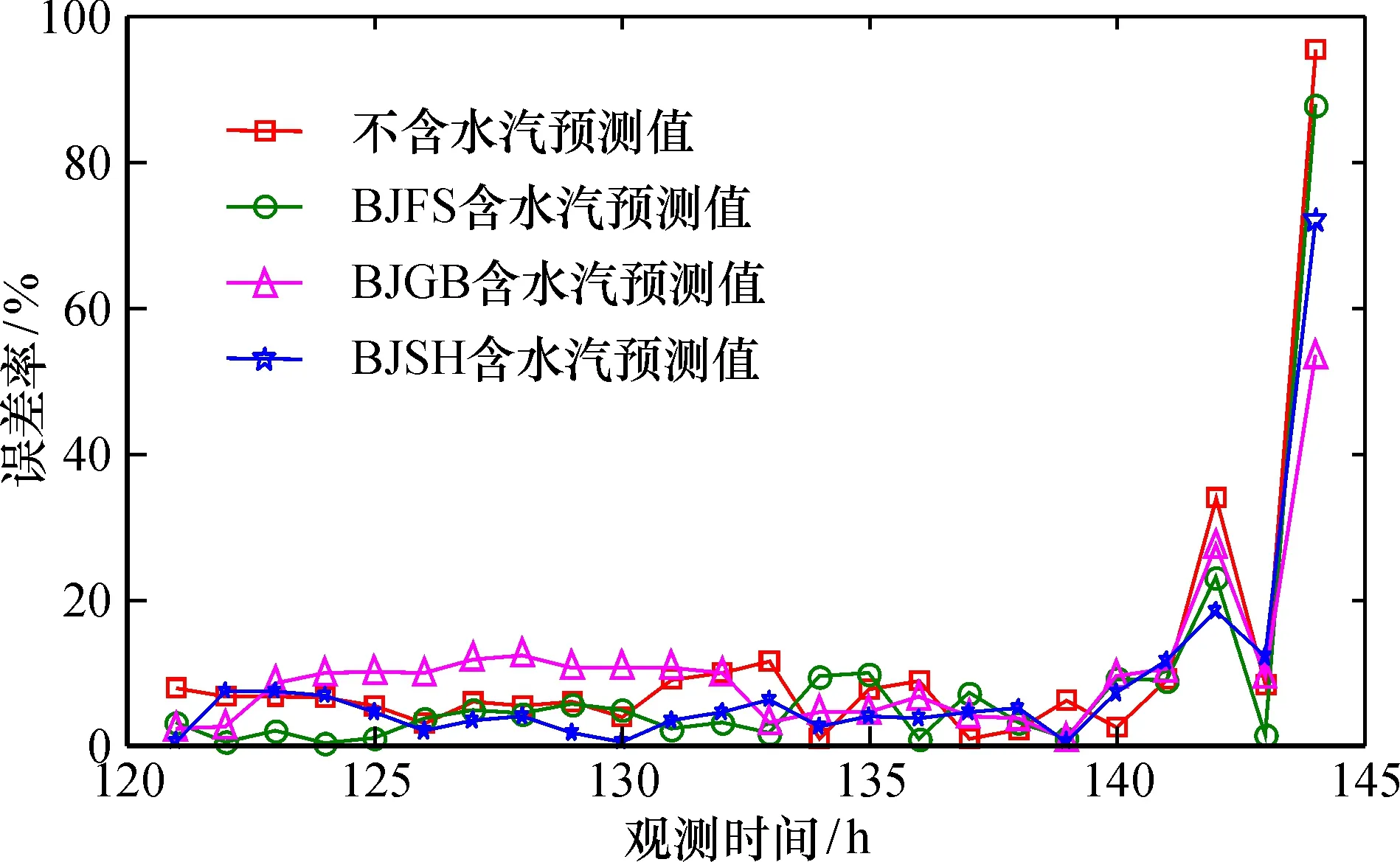
图5 2015年第280天24 h各组GA-BP神经网络预测PM2.5含量相对误差对比Fig.5 Comparison of the relative errors of GA-BP neural network prediction of PM2.5 content in each group on 280th day and 24 hours in 2015

4种预测因素预测值的相对精度在21:00前都比较高, 其相对误差都在10%以内, 在22:00—24:00内, 其预测精度均有所降低。 从24:00整体来看,预报因子中分别包含3个CMONOC站GPS-PWV数据的预测值,相对误差分别为8.2%、 10.2%、 8.1%, 较单纯使用其他影响因子预测的相对误差11.0%分别降低了2.8%、 0.8%、 3%, 其误差相对较稳定。 这表明,引入GPS-PWV数据联合其他影响雾霾的主要大气环境数据和气象数据作为预报因子可明显提高预测PM2.5质量浓度的精度和可靠性。

4 结 论

本文分析了北京市2015年第275～280天各雾霾影响因素与PM2.5质量浓度之间的相关性,为提高模型预测值精度,选取了CO、NO2、SO2、O3、湿度数据并将其分别与BJFS、BJGB、BJSH 3个CMONOC站反演得到的GPS-PWV数据联合作为预报因子的4种情况,采用BP神经网络模型和GA-BP神经网络模型分别预测了PM2.5质量浓度值。通过分析这4种情况下两种模型预测出的PM2.5值与真实值的误差,结果表明:在预报因子不同的条件下,使用GA-BP神经网络模型比BP神经网络模型预测的数据精度更高,更加稳定;在GA-BP神经网络预测PM2.5质量浓度时,利用影响雾霾的主要因子联合不同高程站点的GPS-PWV数据预测的精度有所差异,测站高程与当地高程相差越大,预测值精度相对越低;但就整体而言,使用包含GPS-PWV数据比单纯使用影响雾霾主要的大气环境因素和气象因素作为预报因子的GA-BP神经网络预测值相对误差小,其预测值的精度和可靠性均有所提高;因此,将GPS-PWV数据联合影响雾霾主要的大气环境因素和气象因素作为GA-BP神经网络模型预测PM2.5含量的主要预报因子,有利于提高预测PM2.5含量的精度和可靠性。本文仅针对于北京市的PM2.5预测得到验证,对于其他城市添加水汽因素对于预测PM2.5可以起到一定的参考作用。

表2 不同组预报因子的GA-BP神经网络预测值的相对误差

Table 2 Relative error of GA-BP neural network predictive value for different group forecasting factors %