索道桥施工控制参数的精细数值解析算法

景天虎,王 鑫,刘均利,莫时旭

(桂林理工大学 广西岩土力学与工程重点实验室,广西 桂林 541004)

0 引 言

索道桥作为独具我国西南地方特色的桥梁,虽有学者称其为上承式悬索桥[1],但它与常规公路悬索桥在结构方面存在显著差异。例如,索道桥主跨两端采用滑轮鞍座,在施工过程中锚跨和中(主)跨的钢索是一个自由连通的自适应平衡系统。空缆架设之后随着主跨桥面系的安装,锚跨缆索会因索力增加伸长后引起小部分索段进入主跨。常规公路悬索桥则是在主索丝股架设完成、调准参数后,不允许其在塔顶主鞍座承揽槽内滑移。对于混凝土索塔,在安装主索鞍时一般要设置向边跨侧的预偏量,随着主跨架设进度，逐渐将其顶回成桥状态主塔中心的设计位置[2-6]。

目前,常规公路悬索桥的施工控制理论比较成熟,关于主索架设参数计算方面的研究成果众多[4-8]。鉴于上述结构差异,索道桥施工控制参数计算时不能直接引用这些成果，而专门针对索道桥的研究成果较少。文献[2,9]分别提出的索道桥主索架设参数的算法是基于主跨缆索线形为抛物线的近似解析法,未见公开文献对其计算误差作深入研究。文献[10]将索道桥初态索形假定为悬链线,并认为只建立中跨缆索的模型便能够较好地模拟,对于168 m跨径的中跨缆索就用了336个悬链线单元离散模拟,通过反复迭代试算来寻找符合满足各种要求的缆索线形,计算工作量较大。同时,文献[2,9-10]都未对锚跨缆索线形和倾角对于索道桥施工控制参数的影响进行详尽分析。尽管目前有限元方法比较成熟,以电算软件为其实现工具，大量应用于土木工程结构分析中,但以解析法为基础的各种实用方法仍然具有重要的意义,它们不仅使用方便,而且往往能提供更为清晰的受力概念[11],故本文以黄河白浪索道桥为背景,基于全桥主索无应力索长不变量,按照无应力状态控制法的基本原理[12],统筹考虑锚跨和主跨缆索架设过程中索段的相互转换影响,研究了用于索道桥架设参数计算的精细数值解析算法。

1 解析算法原理

1.1 近似解析法——抛物线法简析

近似解析算法假定索道桥的多根主索受载和变形均匀一致,将其等效为单根索平面模型(图1);假定主跨钢索线形为抛物线,两端铰支在鞍座处主索轴线理论交点A、B处。锚跨主索的水平倾角和垂度影响被忽略;全桥用一个水平索力代替锚、主跨的钢索所有截面的轴向索力;再综合力学平衡和材料物理特性方面的关系,根据同一座索道桥全桥钢索在任意两种荷载状态下的悬索驰度(即各跨无应力索长之和减去水平跨径之和)相等的几何条件,得到一个在所求荷载状态下水平索力的3次代数方程(即悬索的转换方程);最后由已求得的水平索力和力矩平衡条件得到主索线形[2, 9]。

实际上,悬索驰度相等的几何条件就等价于“全桥无应力索长(S0)不变量”的变形协调条件,即近似解析法统筹考虑了主、锚跨索段变形的协调条件。但是该算法在公式推导过程中的多项近似处理,必然会对索道桥主索架设参数的计算精度产生一定程度的影响,值得进一步研究。

目前,索道桥成桥后调整桥面线形是要在拆下桥面系构件的条件下才能进行。显然,主索架设经济且理想的施工工艺是:空索初挂、线形实测精度满足要求后,钢索端部就被永久锚固于锚碇上,全桥钢索的S0随即被固定下来,在后续的施工过程中保持不变,就等于成桥满活载状态下的S0(下文称为“索长不变量”)[12],亦即得到钢索的理论下料长度为S0,再考虑一定的操作长度,即可得到实际的下料长度Sc。

1.2 数值解析算法——分段悬链线法

该算法是在主索线形参数计算时把数值迭代与索段的悬链线解析公式结合起来的分析方法,原本被用于常规公路悬索桥主缆线形计算。悬链线被认为是最接近真实反映实际悬挂钢索的线形。该算法假定主跨钢索线形由分段悬链线组成，两个相邻集中力之间区段的索形为悬链线[6]。

悬链线参数方法又可分为两大类[7]:① 主缆索自重集度按其有应力长度计算作为已知条件的线形公式(式(1)); ② 主缆索自重集度按其无应力长度计算作为已知条件的线形公式(式(2))。

(1a)

(1b)

(2a)

假定钢索为忽略截面泊松比效应的理想柔性索,对图2无集中力作用的索段悬链线形状满足:

(3a)

(3c)

(3d)

图1 索道桥主索计算图式[2,13]Fig.1 Calculation chart for main cables of cableway bridges

其中,hi和li分别为第i索段两端点间的高差和水平投影距离;qi和qi0分别为第i段按钢索有、 无应力长度计算的自重集度;E和A分别为主索材料弹性模量和横截面积;Hi和Hj分别为第i索段左、 右端横截面的水平索力; 索道桥的同一跨钢索中所有索段的水平索力相等, 因此记为Hi=Hj=H;Vi和Vj分别为第i段悬链线左、 右端横截面的剪力;Si和Si0分别为第i段索段的有、 无应力长度; ΔSi为第i索段的弹性伸长量;αi和βi为计算参数。

图2 主索在自重作用下受力分析[4, 7]Fig.2 Mechanical analysis of main cables under dead load

鉴于前述的结构差异,必须对该数值解析算法加以改造,才能用于索道桥的施工控制参数计算。以下将改造后的算法简称为“精细解析法”。

索道桥主跨为其线形控制跨。单个索段的线形参数计算问题解决后,接着分析由分段悬链线索段组成的整个主跨线形参数计算问题。

首先,从主索轴线理论交点A、B(图1)出发,假定该点处的主索水平索力HA、HB和剪力VA、VB(其初值可取近似解析法的计算值), 累加各相关索段的hi，推求跨中垂度和A、B两点高差,并与这两个参数的已知值比较,经迭代得到最终的HA、HB和剪力VA、VB。 同理, 若在图1中把主跨钢索水平索力记作Hm, 则有HA=HB=Hm。

其次, 在图1中假设在点A和点B截面处截断主索, 取出锚索分析。 从空索状态开始施加桥面系恒载过程中, 由水平力的平衡条件可得: 左、 右锚跨的钢索水平索力分别为HmA=Hm+FmA和HmB=Hm+FmB, 其中FmA和FmB分别为钢索在左、 右鞍座处的摩阻力。 滑轮鞍座的摩擦系数可通过试验或《机械技术手册》确定, 结合已求得的RA和RB、FmA、FmB便可得到, 进而HmA和HmB变为已知量。 通常架设阶段的滑轮鞍座处于充分润滑状态,滚动摩阻力FmA和FmB相对于Hm很小, 可略去,则近似有HmA=HmB=Hm。

最后, 把li和hi分别用锚跨的水平跨径和高差代替, 再把HmA、HmB、li和hi代入式(1a)、(1b)(qi已知时)或者式(2a)、(2b)(qi0已知时), 联立求解即可得到VsA、VsB、SsA、SsB(当qi已知时),S0sA、S0sB(当qi0已知时)。 这里SsA、SsB和S0sA、S0sB分别为左、 右端整个锚跨索段的有应力长度和无应力长度；VsA、VsB则为对应的索端剪力。 通过式(1a)～(3d),进而得到锚索其他截面处的架设参数。

2 索道桥施工控制参数计算

2.1 成桥满活载状态下主索安装参数

该荷载状态为设计规定的索道桥运营目标状态。按照桥梁的使用功能要求,主跨钢索跨中垂度值fm0和支点高差hm0,桥面系恒、活载加载参数等由设计者首先拟定,成为图1中所示结构的已知参数。这样就可采用1.2节算法得到主跨和左、右锚跨的无应力索长,这里分别记作S2和S1、S3,进而得到全桥无应力索长不变量S0=S1+S2+S3。

2.2 平衡状态下主索的变形协调函数

在某施工工况的荷载平衡状态下,假设主跨钢索的无应力索长为S0x和跨中垂度为fmx,两个锚跨的无应力索长之和为l0s,全桥钢索总的无应力索长等于运营目标状态的索长不变量,即

S0x+l0s=S0,

(4a)

对式(4a)取全微分, 可得

dS0x=-dl0s。

(4b)

可见, 索道桥钢索的无应力索长会在锚跨和主跨之间出现此消彼长的转换状态, 以适应不同的荷载工况, 同时满足各跨之间钢索的变形协调条件。 由式(4a)知, 锚索的无应力索长l0s是S0x的函数; 而S0x又是fmx的函数, 故记作l0s=l0s(S0x);S0x=S0x(fmx); 进而l0s=l0s(fmx)。再定义变形协调函数

g(S0x)=S0x+l0s(S0x)-S0

=S0x(fmx)+l0s(fmx)-S0

=g(fmx)=0。

(4c)

如果主索的某个平衡状态位形存在, 必然有与其对应的S0x和fmx满足式(4c), 即该方程有解。 式(4c)是关于fmx的隐函数方程, 可用牛顿求根法迭代计算得到数值解。 迭代收敛准则可根据主索制作下料精度确定。 迭代格式为

(5)

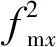
2.3 空索和成桥恒载工况的主索架设参数

空索工况的全桥主索无应力索长等于索长不变量S0。由无应力状态控制原理可知[12],分阶段成形结构的4个条件(外荷载、结构体系、支承边界条件、构件单元的无应力状态量)唯一地确定一个施工阶段的平衡状态;通过求解式(4c)的未知数fmx即可确定该工况的主跨钢索跨中垂度值,进而得到主、锚跨的全部线形参数。同理,可得到成桥恒载工况的主、锚跨的全部线形参数。

2.4 主索架设参数的温度修正

设钢索端部锚固时的温度为t0,则可由2.1～2.3节所述方法确定在t0温度下钢索无应力长度S0t0,以及相对应的成桥恒载、空索或活载工况的其他架设参数(包括主跨跨中垂度fmx,t0)。在若某一工况的某时刻温度为t, 相应的钢索无应力长度为S0t,则有[10]

S0t=S0t0+α·(t-t0)·S0t0,

(6)

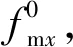
3 工程背景

白浪索道桥是一座主跨径438 m单车道桥梁(图3)[2,14]。设计采用的满载跨中矢度为1/39;主要活载图式为3×40 t、纵桥向车距150 m的履带车队。桥梁上部结构的主要参数为:沿顺桥向布置43道钢横梁,质量1.1 t(30道)和1.2 t(13道)两种梁相间布置, 间距为7.75～11.25 m。 主索采用76根钢丝绳(直径38 mm, 绳股结构6×37+FC, 标准强度1 770 MPa); 4根抗风索。 桥面板为东北松木板(长×宽×高为4.4 m×0.5 m×0.085 m), 约876根。

图3 白浪索道桥平、立面示意图Fig.3 Schematic diagram of plan and elevation of the Bailang cableway bridge1—外稳定索;2—内稳定索;3—桥面索;4—抗风索;5—桥面板;6—横梁

4 施工控制参数计算结果的精度对比

本文第3节的案例摘自文献[2]的实例Ⅱ。 现取其中1根钢索建立计算简图(图1)。材料参数:钢索弹性模量E=1.079 1×108kN/m2;每根钢索截面面积A=5.891 3 cm2;主跨桥面系自重为2.491 74 kN/m,76根钢索总自重为4.090 77 kN/m(文献[2]按纵桥向沿水平跨径给出该参数; 本文计算时随着线形迭代进程将其化为沿有应力曲线索长的集度qi)。几何参数k、p、w、z、e、l、L分别为67.5、 82、 46.25、 23.25、 150、 32.5、 438 m;k′、p′、w′、z′、e′、l′分别等于k、p、w、z、e、l; 锚索水平倾角参数γ=λ, 分别取0°、 30°(文献[2]未给出该参数; 其采用近似解析法计算, 不需要这些值)。荷载参数P1、P2、P3分别等于10.791、 11.772、392.4 kN。不计滑轮鞍座滚动摩阻力;以主索端部锚固时刻为基准,分别考虑温度变化±5 ℃的情况。使用Matlab软件编程执行2.2节所述1～2轮次迭代计算,得到的施工控制参数结果见表1、2。

需说明的是,文献[2]只给出了钢索的水平索力和主跨跨中垂度值,未计算温度变化工况。本文“近似解析法”的主跨索长值则是把文献[2]的相关参数值代入抛物线索形长度的精确解析公式求得的。表1中的“有限元法”结果是采用ANSYS软件实现的“模型更补法”的计算结果。文献[15]已深入比较了“分段悬链线法”和有限元法对于理想柔性索的索形模拟精度。考虑本分析的结构严谨性、又限于篇幅,在表1中有限元法的结果仅列出了荷载工况Ⅲ在锚索水平倾角0°时的计算结果,以验证算法精度。

(1)从索长计算结果可见:有限元法与精细解析法的索形参数结果非常接近,水平索力值的相对偏差在0.121%以内，这说明精细解析法的分析结果是可靠的。

(2)从空索初挂到成桥满活载工况,随着主跨荷载的增加,锚索无应力长度逐渐减小,而主跨钢索的无应力长度逐渐增大;钢索无应力索段长度在主、锚跨之间进行此消彼长的相互转换,其幅度大于71mm,超过了规范(JTG F80/1—2004)关于“成品索股长度”项目允许偏差(索股长/10 000; 本例限值为43.8 mm),故不同施工阶段索长控制参数计算时应该予以考虑。

(3)锚索水平倾角从0°增加到30°, 引起水平索力的相对变化量小于1.04%; 而全桥主索无应力索长变化量大于9.953 m, 远远超过限值43.8 mm, 故锚跨倾角的影响不容忽视。 在考虑和忽略锚索的自重垂度效应的两种情况下,精细解析法得到的全桥主索无应力索长差值都在3 mm以内。锚索跨中垂跨比非常小(本例不超过1/1 038),而索道桥主索的拉力在空索状态就接近了容许拉力的70%,再结合钢索的修正弹性模量Ernst公式,这从理论上也证明:忽略锚跨钢索的垂度对问题求解精度影响很小。

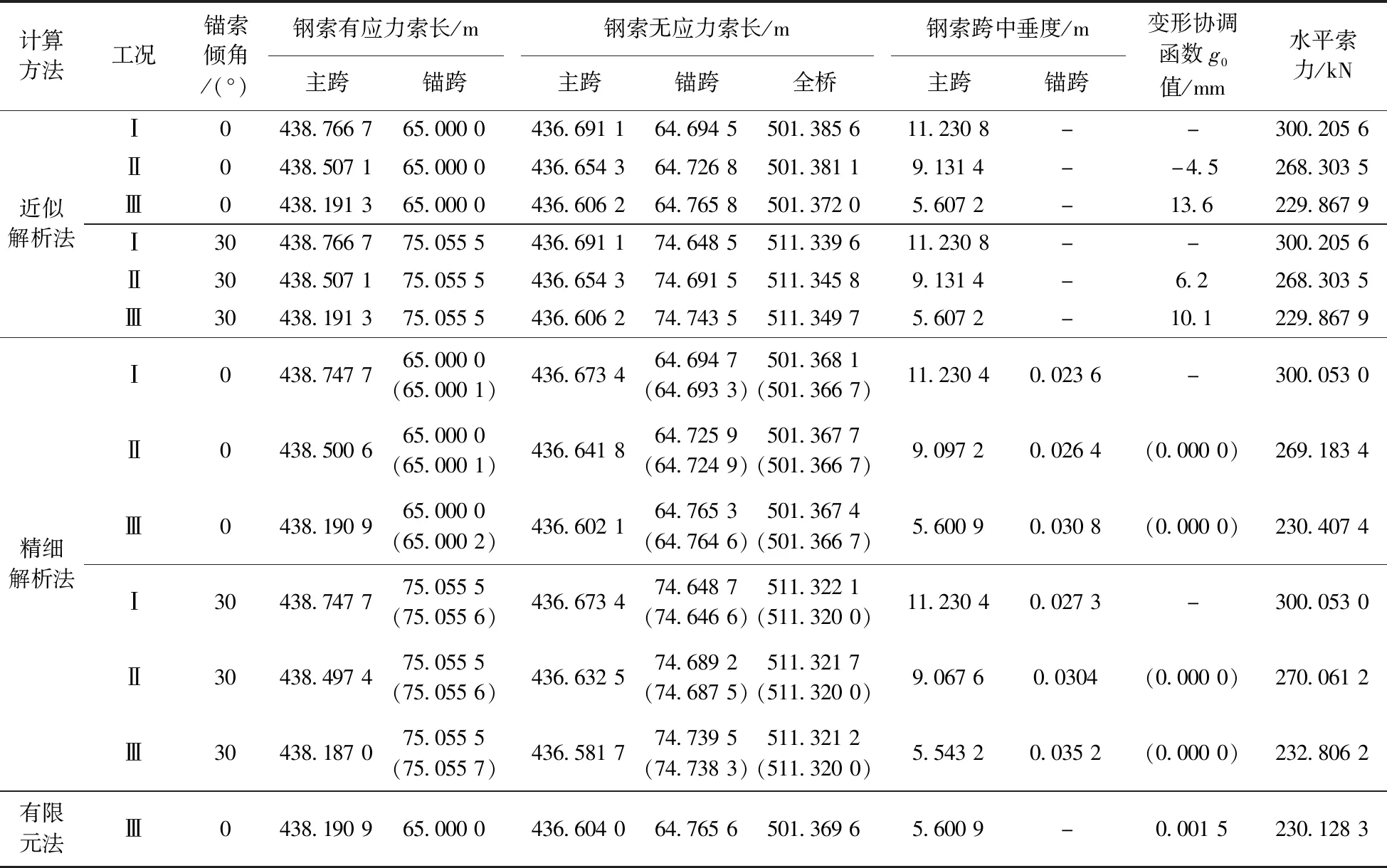
表1 锚固时刻主索施工控制参数

注:(1)工况Ⅰ、 Ⅱ、 Ⅲ分别代表成桥满活载状态、 成桥恒载状态、 空索状态; (2)在“数值解析算法”结果中, “65.000 0 (65.000 1)”分别表示不计和计入锚索跨中垂度的计算值,其他类似表示均为此意义; (3)求解工况Ⅱ、Ⅲ的参数值时使用的全桥索长不变量是在工况Ⅰ条件下计入锚索跨中垂度的数值; (4)锚跨的“钢索有(无)应力索长”为左、右锚跨的合计值。

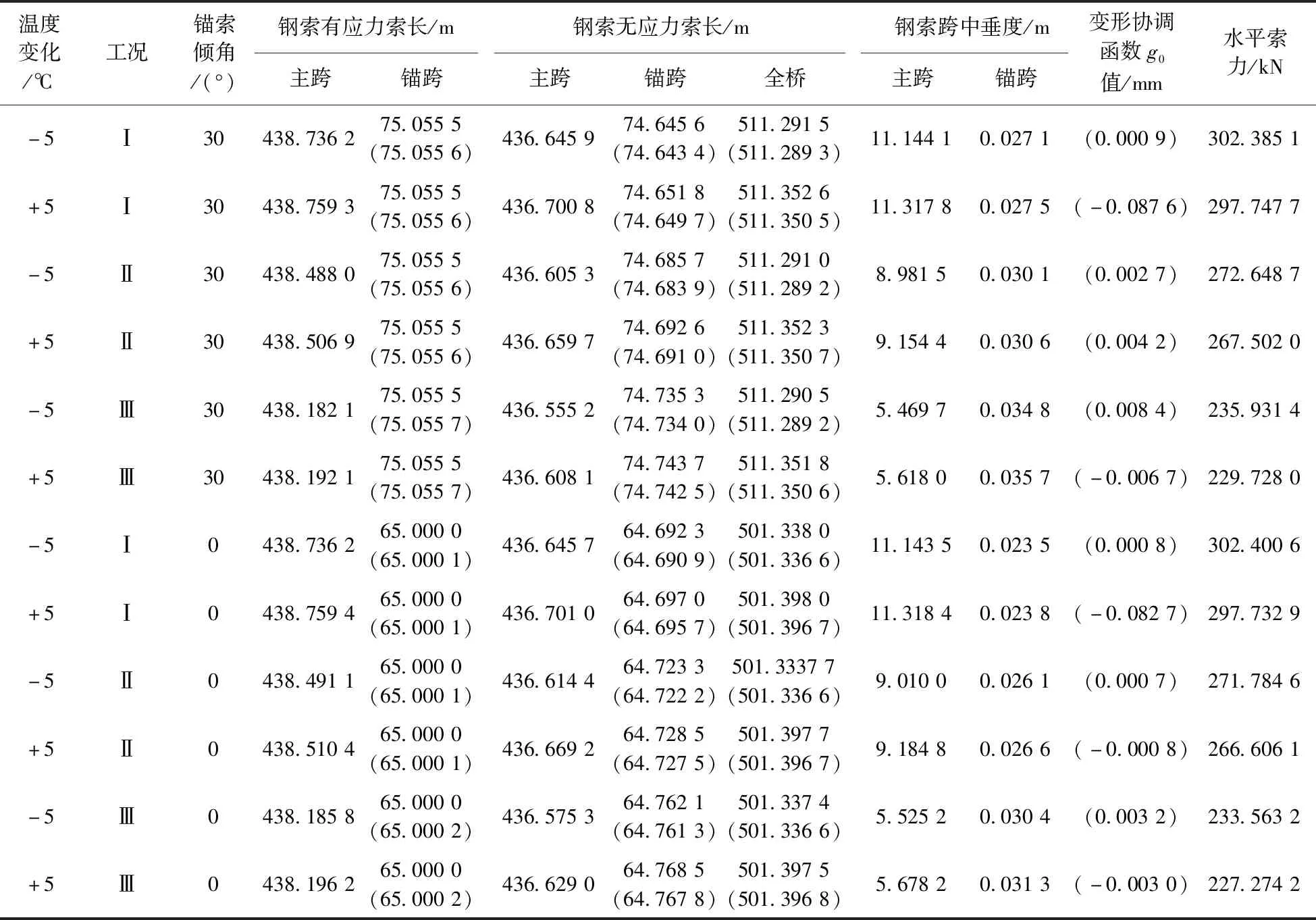
表2 温度变化后的主索施工参数

(4)从计算结果表1看,锚索倾角对主索受力、线型的影响相对值较小,对桥梁的设计、使用几乎无影响。这是由于在成桥状态悬索桥主缆线形确定时,对线形跨控制跨(一般为中跨)的主缆垂度可根据设计条件事先确定下来; 而对于非线形控制跨(一般为边跨),主缆水平张力可根据线形控制跨成桥状态线形已经确定,边、中跨主缆的水平分力相等求出来[15]。索道桥桥型可以归入悬索桥结构大类中[1],前者的锚跨相当于一般公路悬索桥的边跨,因此索道桥主索遵从悬索桥主缆线形确定的一般规律。

(5)温度变化±5 ℃引起的水平索力相对变化量小于1.37%, 全桥无应力索长变化量也小于31 mm, 但主跨跨中垂度的变化量超过73 mm, 超过了规范(JTG F80/1—2004)关于“中跨跨中基准索股高程”项目允许的偏差限值(中跨跨径/20 000; 本例限值为21.9 mm)。

(6)比较近似解析法和精细解析法的计算精度。后者的变形协调函数值不超过0.087 6 mm,远远低于前者的结果(其最大值为13.6 mm),即精细解析法的参数计算结果高精度地满足了一般材料力学解答关于构件变形协调条件的要求,其计算结果较近似解析法更符合结构的实际状态,并且迭代计算量也不大,算法效率较高。以精细解析法的参数计算结果为基准来评价近似解析法施工控制参数的计算精度。从表1结果可以推算出,近似解析法的全桥无应力索长最大误差值(28.5 mm)未超过限值43.8 mm;而在工况Ⅱ的锚索倾角0°、工况Ⅲ的锚索倾角0°和30°情况下,主索跨中垂度误差值,都超过了限值21.9 mm。主索水平索力的计算值相对误差不超过1.26%,满足一般工程精度(误差限值5%)的要求。当温度变化5 ℃时,由文献[2]27页公式可得主索水平索力变化量的近似值为3.814 4 kN,而精细结果显示该值在2.305 3～3.155 8 kN变化。由此可见,近似值偏大,相对误差超过20.87%。

5 结 论

(1)施工过程中钢索无应力索段长度在主、锚跨之间呈现此消彼长的转换现象,其幅度超过了索长误差限值。

(2)锚索倾角对主索受力、线型的影响,其相对值较小,对桥梁的设计、使用几乎无影响。锚索的自重垂度效应对全桥无应力索长求解精度影响很小,可以忽略;锚跨倾角和温度变化的影响,则不容忽视。

(3)近似解析算法得到的水平索力值能满足一般工程精度的要求,但其他架设参数的计算误差超限,不满足大跨度桥梁施工监控的精度要求。

(4)精细解析算法的计算结果高精度地满足了构件变形协调条件,算法效率较高。