多孔能源材料在有限扩散条件下的Warburg阻抗谱仿真研究

2019-08-27杨维明黄秋安李伟恒李喜飞张久俊

西安理工大学学报 2019年2期

李雨，杨维明，黄秋安，李伟恒，李喜飞，张久俊,

(1.湖北大学计算机与信息工程学院, 湖北武汉430062; 2.上海大学理学院/可持续能源研究院，上海200444；3.西安理工大学先进电化学能源研究院，陕西西安710048)

在电化学能源存储和转换领域，电化学阻抗谱可能是应用最为广泛的表征技术[1]。通过将测试的阻抗谱数据拟合到选定的等价电路模型，或者通过分析阻抗谱数据的特征时间常数分布以解析电池内部物理和电化学过程对应的极化损失和动力学特征参数，对发展高性能的电极和电解质十分重要。当前，这种基于阻抗谱模型的方法，在极化损失分析和动力学特征参数解析中应用非常普遍[2]。

电化学能源存储和转换器件的电极微观结构是三维的，然而大多数等价电路模型单元(比如电阻、电感和电容)是零维的。因此，这种维度的不匹配，导致基于等价电路模型的阻抗谱诊断方法先天不足。不同于零维的等价电路单元模型，Warburg阻抗模型常常被用来仿真理想的一维扩散过程。这些扩散过程可以依据彼此对应的边界限制条件来分类[3]。这些边界限制条件包括狄拉克条件(即特定浓度)、纽曼条件(即特定流量)和半无限条件(即浓度为零且流量为零)。利用这些一维边界限制条件可以得到Warburg阻抗模型的解析解或者近似解，使基于电路模型的阻抗方法的计算成本有所降低。

Warburg阻抗模型具有准一维的内在属性，而多孔电极具有三维的微观结构。因而，Warburg阻抗模型应用于多孔电极时，首先要求多孔电极的三维微观结构信息可以采用若干本体参数近似描述。阻抗谱作为一个非常敏感的间接诊断工具，其观测结果往往具有多样性和敏感性。因此，只有预先了解Warburg阻抗谱与孔隙结构参数和材料本体参数的内在关系，才可能辨识Warburg阻抗模型的能力边界：可以做什么，不可以做什么，以及面临的主要挑战是什么。掌握了Warburg阻抗模型的能力边界，才可能更好地利用Warburg阻抗模型的诊断功能[4]。

本研究以充满电解液的圆筒形单孔为例，建立了有限扩散条件下的Warburg阻抗单孔数学模型，并通过数值计算仿真，重点研究了孔的直径、孔的深度、电解液单位长度电阻率以及电极活性物/电解液界面单位长度比电容对Warburg阻抗行为特征的影响，尤其关注上述参数与Warburg阻抗的动态演化趋势，即有限扩散Warburg阻抗谱和半无限扩散Warburg阻抗谱的内在联系。本文仿真研究的结果，为深入理解储能材料中多孔电极的行为特征，尤其是优化储能器件能量储存密度和最大功率输出密度提供了有价值的理论依据。

1 Warburg 阻抗谱模型理论

1.1 Warburg阻抗谱模型类型

电活性物质的扩散过程，是在驱动力的驱动下扩散，不同的边界条件可能会产生不同的Warburg阻抗[5]。图1为充满电解液的单孔在不同频率电流信号激励下，金属离子的渗透深度示意图[6]。图1(c)和图1(d)所示孔隙充满电解质溶液，孔壁为电子导体，其中L为圆柱形孔的深度，λ为圆柱形孔的直径。当浓度梯度为主要驱动力，离子通过充满电解质溶液的多孔电极时，Warburg扩散阻抗不可避免。

根据反应物M的浓度值和流量大小的不同，Warburg阻抗模型可以分为三种类型：

(1)

(2)

s=TDω

(3)

(4)

(5)

式中，j为虚数单位；RD是扩散阻力；s是一个无量纲频率；ω是径向频率；TD是一个与扩散相关的时间常数；D是扩散反应物的有效扩散系数；le是有效扩散厚度；σ是Warburg系数；C是扩散反应物的浓度；A是电极或电解质界面表面积；R是气体常数；T是相对温度；n是电子转移数量；F是法拉第常数。

(6)

s=TDω

(7)

(8)

式中，fk为转折频率。

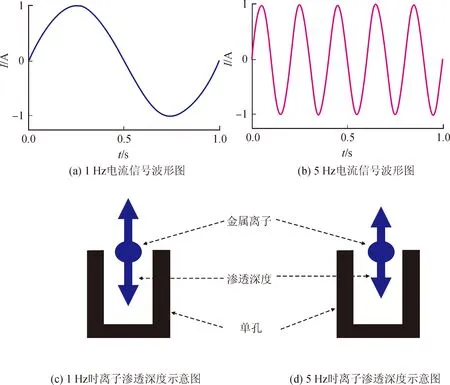
图1 单孔孔隙中充满电解质溶液时不同频率电流信号激励下金属离子渗透深度示意图Fig.1 Schematic of penetration depth of metal ions in a single pore filled with electrolyte solution simulated by current signals at different frequencies

3) 在无限扩散长度的极限情况下，即l→∞或者扩散系数D很小时，上述两种阻抗相等，即ZWs|le→=ZW0|le→，此时Warburg阻抗模型进一步退化为半无限扩散阻抗Z[9]，其具体表达式为：

(9)

三种情况下的扩散阻抗均可以称为Warburg阻抗ZW，三种情况下扩散阻抗的相同点是：①在高频时，扩散反应物不需要大幅度扩散,从而Warburg阻抗很小；②在低频时，扩散反应物需要扩散的深度更深，故Warburg阻抗比较大。

1.2 双曲正切余切函数

单孔Warburg阻抗模型的核心是双曲正切余切函数(如图2所示)，此处对该函数做一个简单概述，为下文讨论做一些数学铺垫。coth函数为双曲余切，它是双曲正切函数tanh函数的倒数，双曲函数在物理学众多领域可找到丰富的应用实例，例如阻力落体、导线电容、粒子运动、非线性方程和悬链线等物理研究。无论是在经典或近代的物理学内容中，还是在正在发展的物理学内容中，双曲函数具有不可或缺的重要作用。双曲余切可由基础双曲函数双曲正弦和双曲余弦推导而来[10]：

(10)

(11)

由图2可知，coth函数图像分为两部分，分别在第一和第三象限，且两个部分均是单调递减的趋势。函数的定义域是{x|x≠0}，值域是{y||y|>1}。coth函数有三条渐近线，水平渐近线为y=±1，垂直渐近线为x=0。

图2 双曲余切与双曲正切函数关于自变量的函数图Fig.2 Diagrams of hyperbolic cotangent and hyperbolic positive tangent functions with respect to independent variables

1.3 单孔Warburg阻抗谱模型Zp

电极活性层/电解液界面之间存在多个不相同但均充满电解液的孔隙，当前选取一个孔隙为例，讨论Warburg阻抗与孔隙结构参数和材料本体参数之间的定量关系。通常情况下，充满电解质溶液的圆柱形孔，其整体Warburg复阻抗Zp为[11]：

(12)

(13)

(14)

式中，ri为沿圆柱孔轴向方向单位长度电解质溶液的电阻；ρi为电解质溶液的电阻率；λ为孔的直径；L为孔的深度；zi和z′i分别为圆柱形孔隙中活性物/电解质界面的单位长度复阻抗和单位面积复阻抗。

考虑单个圆柱形孔，其孔隙内沿轴向方向电解质溶液总欧姆电阻rp和孔壁活性物/电解质溶液界面总复阻抗zp可重新定义为：

rp=riL

(15)

(16)

将式(15)、(16)代入式(12)，得到充满电解质的圆柱形孔的总复阻抗为：

(17)

针对单个圆柱形孔，定义圆柱形孔内壁与孔隙内电解质溶液所形成界面为活性层/电解液界面，界面复阻抗的特性可以分为理想界面和非理想界面两大类。理想界面常采用理想电容来仿真，非理想界面常采用常相位单元来仿真，当前只考虑理想界面。

当活性物/电解质溶液的界面特性表现为理想电容时，其活性层/电解液界面总复阻抗可重新表达为[12]：

(18)

其中，ci为活性层/电解液界面单位长度比电容,将式(18)和式(15)代入式(17)，可得：

(19)

如果令

τ=L2ciri

(20)

则式(19)可重写为：

(21)

根据式(10)所定义的双曲余切函数，超越函数式(21)可重新组织为：

(22)

为了继续简化超越函数式(22)，列出式(23)和(24)：

(23)

(24)

联立式(23)和(24)可得：

(25)

将式(25)代入式(22)，由此可得单孔Warburg阻抗模型的代数函数表达式：

(26)

经过上述简化处理，至此已得到在理想界面和有限扩散条件下，充满电解液的单孔Warburg阻抗模型，该模型不是超越函数形式，而是常规的代数函数形式。单孔Warburg阻抗模型从超越函数简化到代数函数，这为其计算机仿真分析扫清了障碍。

如图3所示，fk=10 Hz为转折频率，离子迁移从扩散区进入了饱和区。图中参数取值为L0=0.2 μm，ci0=500 F/m，ri0=5.0×109Ω/m，频率范围为0.1 Hz～10 kHz，Z′和Z″分别为Warburg阻抗实部和虚部。此频率越高，表示离子的迁移速度越快。如果该阻抗谱图来自于超级电容器或者锂离子电池，越高的转折频率对应越高的最大输出功率密度。

图3 Warburg阻抗谱图Fig.3 Plot of Warburg impedance spectra

截至目前，在理想界面和有限长度扩散条件下，充满电解质溶液的圆柱形单孔Warburg阻抗谱模型已经建立，模型中不仅成功嵌入了孔的直径、孔的深度、孔隙内电解质溶液电导率以及电极活性层/电解液界面单位长度比电容等参数，而且从超越函数方程简化为代数函数方程。上述工作，为下文有限扩散条件下单孔Warburg阻抗谱仿真研究做好了理论准备。

2 有限扩散条件下Warburg阻抗谱仿真分析

在有限长度扩散的边界限制条件下，进行理想界面条件下Warburg阻抗谱仿真分析，重点研究Warburg阻抗谱随孔的直径、孔的深度、孔隙内电解质溶液电导率以及活性层/电解液界面单位长度比电容等参数的演化规律，为实现理想界面条件下Warburg阻抗谱的有效分析提供精细的参考模板。

2.1 Warburg阻抗谱：孔的深度L

为了研究孔隙深度与Warburg阻抗谱的演变关系[13,14]，可以先固定单位长度比电容ci与单位长度电阻ri，不妨假设ci0=500 F/m与ri0=5×109Ω/m。图4显示了理想界面情形Warburg阻抗谱随孔的深度L的演变关系。L变化范围为：L0=0.2μm，L1=0.4μm，L2=0.8 μm，L3=1.2 μm和L4=1.6 μm。其中界面单位长度比电容ci0与单位长度电阻ri0固定，频率范围为0.1 Hz～10 kHz。

图4 Warburg阻抗谱随孔的深度L的演化趋势Fig.4 Evolution trend of Warburg impedance spectra with respect to pore depth L

由图4可知，当孔的深度L发生变化时，其对理想界面Warburg阻抗谱的影响不仅体现在下限频率区域，而且体现在半无限扩散区。

1) 在高于转折频率且频率趋向增加的区域，即电荷半无限扩散区，孔的深度L增加，扩展了半无限扩散区，压缩了电荷饱和区。具体而言，当孔的深度从0.2 μm增加到1.2 μm时，Warburg阻抗谱转折频率fk从10 Hz单调减小到0.15 Hz，而且横跨45°Warburg区的低频电阻RW从0.29 kΩ增加到2.09 kΩ，转折频率fk的降低和低频电阻RW的增加均表明电荷快速传输到深孔的能力变弱。当孔的深度L增加到1.6 μm时，“电荷饱和区”在阻抗谱图中几乎被“半无限扩散区”完全覆盖，理想界面从有限长度Warburg阻抗谱几乎蜕变为半无限扩散Warburg阻抗谱。

2) 在低于转折频率且向频率下限趋近的区域，孔的深度L对Warburg阻抗谱的影响效果同样明显，体现在Warburg阻抗谱在下限频率处对应复阻抗的虚部极值。具体而言，当孔的深度从0.2 μm增加到1.6 μm时，在下限频率fL=0.1 Hz处，Warburg复阻抗虚部的绝对值从15.9 Ω减小到2.6 Ω，对应于低频等效电容从10 μF增加到600 μF。可见，在其他参数不变的条件下，增加孔的深度L，虽然有利于增加电荷存储容量，但是不利于提高电荷传递速度。

从电化学动力学的角度来理解Warburg阻抗谱随孔的深度L的演化规律。①不变量。表征电荷传输阻力大小的电解液单位长度电阻ri0=5×109Ω/m、表征界面电荷储存能力的活性物/电解液界面单位长度比电容ci0=500 F/m、以及表征最长观测时间窗口的下限频率fL=0.1 Hz(对应观测时间周期TL=10 s)，这三个要素同时固定。②变量。表征电荷离子传输路径长度的孔的深度L变化。③变量与不变量的竞争效应。L增加意味着电荷离子传输路径长度增加，ri0=5×109Ω/m固定意味着电荷离子传输遇到的阻力不变，ci0=500 F/m固定意味着界面储存电荷能力不变，fL=0.1 Hz固定意味着电荷离子传导所对应观测时间周期不变。上述变量与不变量的竞争结果：增加L预示电荷离子传输路径长度的增加，而增加传输路径长度预示界面长度的增加，界面长度的增加预示低频电阻RW的增加和界面可储存电荷总量的增加，但是电荷离子的输运能力和输运时间没有同步提高，这一矛盾，一方面导致电荷传递能力的相对下降，这点体现在转折频率fk和低频电阻RW上；另一方面，当L增加到一定程度时，必将导致界面可储存电荷总量远远高于经过传导输运到达界面的电荷数量，此时，阻抗谱从有限长度Warburg扩散模型退化为半无限Warburg扩散模型。

2.2 Warburg阻抗谱：单位长度比电容ci

为了研究活性层/电解液界面单位长度比电容ci对Warburg阻抗谱的影响[15,16]，先固定孔的深度L与单位长度电阻ri，不妨假设L0=0.2 μm与ri0=5×109Ω/m。图5显示了理想界面Warburg阻抗谱随单位长度比电容ci的演变关系。图中界面比电容ci变化范围为：ci1=300 F/m，ci2=400 F/m，ci0=500 F/m，ci3=1×103F/m，ci4=2×103F/m和ci5=2×104F/m，ci6=4×104F/m和ci7=8×104F/m。其中，孔的深度与单位长度电阻固定，频率范围设定为0.1 Hz～10 kHz。当活性物/电解液界面单位长度比电容ci发生变化时，其对理想界面Warburg阻抗谱的影响主要体现在低于转折频率的电荷饱和区，而对高于转折频率的半无限扩散区的影响几乎可以忽略。

1) 中高频区。在高于转折频率且频率趋向增加的区域，即电荷半无限扩散区，单位长度比电容ci增加，压缩了电荷饱和区，扩展了半无限扩散区频率范围，但是横跨45°Warburg区低频电阻几乎保持不变，即RW≈0.31 kΩ。具体而言，当ci从300 F/m逐渐增大到2×104F/m时，Warburg阻抗谱转折频率从15 Hz单调减小到0.2 Hz，表明在电荷扩散区的频率范围变宽，电荷饱和区变窄；当ci从4×104F/m继续增加时，“电荷饱和区”在阻抗谱图中几乎被“半无限扩散区”完全覆盖，理想界面从有限长度Warburg阻抗谱蜕变为半无限扩散Warburg阻抗谱。

2) 中低频区。在低于转折频率且向频率下限趋近的区域，单位长度比电容ci对Warburg阻抗谱的影响，主要体现在Warburg在下限频率所对应的复阻抗虚部上。具体而言，当ci从300 F/m逐渐增大到2×104F/m时，在下限频率fL=0.1 Hz处，Warburg复阻抗虚部的绝对值从26.6 Ω减小到0.45 Ω，对应于低频等效电容从60 μF增加到3500 μF。可见，在其他参数不变的条件下，增加界面单位长度比电容ci，虽然有利于增加电荷存储容量，但是未能同步提高电荷输运速度。

从电化学动力学的角度来解释Warburg阻抗谱随单位长度比电容ci的演化规律。①不变量。表征电荷传输阻力大小的电解液单位长度电阻ri0=5×109Ω/m、表征电荷离子传输路径长度的孔的深度L0=0.2 μm、以及表征最长观测时间窗口的下限频率fL=0.1 Hz(对应观测时间周期TL=10 s)，这三个要素同时固定。②变量。表征电荷储存能力的活性物/电解液界面单位长度比电容ci变化。③变量与不变量的竞争效应。ci增加意味着界面储存电荷能力增加，ri0固定意味着电荷离子传输过程中遇到的阻力不变，L0固定意味着电荷离子传输路径长度不变，fL固定意味着电荷离子传导所对应观测时间周期不变。上述变量与不变量的竞争结果：增加ci导致界面可储存电荷总量增加，但是电荷离子的输运能力并没有同步提高，这一矛盾，一方面导致电荷传递能力的相对下降，这点体现在转折频率上；另一方面，当ci增加到一定程度时，导致界面可储存电荷总量远远高于传导输运到达界面的电荷数量，此时，阻抗谱从有限长度Warburg扩散模型退化为半无限Warburg扩散模型。

图5 Warburg阻抗谱随界面单位长度比电容ci的演化趋势Fig.5 Evolution trend of Warburg impedance spectra with respect to ci

2.3 Warburg阻抗谱：单位长度电阻ri

为研究孔隙内电解液单位长度电阻与总阻抗的关系[15,17]，将式(26)中孔深度L与界面单位长度比电容ci设为固定值，不妨假设L0=0.2 μm和ci0=500 F/m。依据上述设定参数和式(26)所定义阻抗谱模型，可以计算得到理想界面Warburg阻抗谱随孔隙内电解液单位长度电阻ri的演化趋势图，如图6所示。图中ri变化范围为：ri1=1.25×109Ω/m，ri2=2.5×109Ω/m，ri0=5.0×109Ω/m，ri3=1.0×1010Ω/m，ri4=2.0×1010Ω/m，ri5=1.0×1011Ω/m，ri6=2.0×1011Ω/m，ri7=4.0×1011Ω/m。其中，孔的深度与界面单位长度比电容固定，频率范围为0.1 Hz～10 kHz。

图6 Warburg阻抗谱随孔隙内电解液单位长度电阻ri的演化趋势图Fig.6 Evolution trend of Warburg impedance spectra with respect to ri

由图6可知，当孔隙内电解液单位长度电阻ri发生变化时，主要影响Warburg阻抗谱转折频率和中高频区的半无限扩散过程，几乎不影响Warburg复阻抗所对应的低频极限电容。

1) 中高频区，为高于转折频率且频率趋向增加的区域，即电荷半无限扩散区。一方面，当ri从1.25×109Ω/m增加到2.0×1011Ω/m时，转折频率fk从30 Hz单调减小到0.2 Hz。fk的减小不仅预示半无限扩散区向低频方向扩展，而且意味着电荷饱和区被“挤压”至更低频率区间，因此，在下限频率fL=0.1 Hz固定的条件下，Warburg阻抗谱观测结果为半无限扩散区频率范围变宽和电荷饱和区被压缩变窄。当ri增加至4.0×1011Ω/m时，半无限扩散区占据整个观测频率范围，电荷饱和区被压缩至完全不可见，此时，阻抗谱从有限长度扩散Warburg模型特征退化为半无限扩散Warburg模型特征。另一方面，当ri从1.25×109Ω/m增加到2.0×1011Ω/m时，横跨45°Warburg区低频电阻RW从0.08 kΩ增加到11.50 kΩ，RW的急剧增加意味着电荷输运阻力的增加，这不利于储能器件最大功率密度的提高。

2) 中低频区，为低于转折频率且向频率下限趋近的区域，即电荷饱和区。当ri从1.25×109Ω/m增加到2.0×1010Ω/m时，在下限频率fL=0.1 Hz处，Warburg复阻抗虚部的绝对值近似保持15.98 kΩ，理想界面Warburg复阻抗的低频极限电容也近似维持不变(CL≈100 μF)，当ri增加到2.0×1011Ω/m，低频极限电容略有降低(CL≈89 μF)。可见，在其他参数不变的条件下，增加孔隙内电解液单位长度电阻ri，几乎不影响界面电容的电荷存储容量，但是显著降低电荷输运速度。

从电化学动力学的角度来解释Warburg阻抗谱随孔隙内电解液单位长度电阻ri的演变规律。①不变量。表征电荷离子传输路径长度的孔的深度L0=0.2 μm、表征电荷储存能力的活性物/电解液界面单位长度比电容ci0=500 F/m、以及表征最长观测时间窗口的下限频率fL=0.1 Hz(对应观测时间周期TL=10 s)，这三个要素同时固定。②变量。表征电荷传输阻力大小的电解液单位长度电阻ri变化。③变量与不变量的竞争效应。ri增加预示电荷离子传输过程遇到的阻力增加，传输阻力增加将导致电荷离子传输速度的降低，L0固定预示电荷离子传输路径长度不变，fL固定预示电荷离子传导所对应观测时间周期不变，ci固定预示界面可储存电荷总量不变。上述变量与不变量的竞争结果：增加ri导致电荷离子的传输速度降低，但是界面单位长度比电容ci储存电荷的容量没有减少，这一不平衡，一方面体现在电荷传递能力相对于电荷储存能力的不足，进而体现为横跨45°Warburg区低频电阻RW的增加和转折频率fk的降低；另一方面，当ri增加到一定程度时，导致经由传导输运到达界面的电荷数量远远低于界面可储存电荷总量，此时，阻抗谱从有限长度Warburg扩散模型退化为半无限Warburg扩散模型。

2.4 Warburg阻抗谱：孔的直径λ

为研究孔的直径对有限扩散条件下Warburg阻抗谱的影响[15,18]，将式(20)中孔的深度L与界面单位长度比电容ci设为固定值，L0=0.2 μm与ci0=500 F/m，同时将式(13)中电解液的电阻率设定为ρi0=4×10-3Ω·m[19]，频率取值范围为0.1 Hz～10 kHz。依据上述设定参数和式(26)所导出的Warburg阻抗谱模型，然后选取孔的直径λ1=0.8 μm，λ2=0.4 μm，λ3=0.2 μm，λ4=0.15 μm，λ5=0.1 μm。根据式(13)计算出相应的孔隙内电解液单位长度电阻ri，将各个对应的ri代入式(20)计算出特征时间常数τ，将上述参数代入式(26)中，可计算得出理想界面半无限扩散条件下Warburg阻抗谱。图7显示了Warburg阻抗谱随孔直径λ的演变趋势。

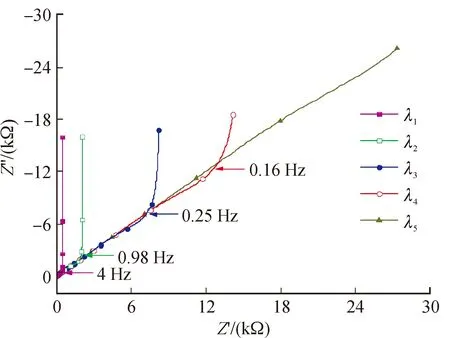
图7 Warburg阻抗谱随孔的直径λ变化的演化趋势图Fig.7 Evolution trend of Warburg impedance spectra with respect to pore diameter λ

由图7可知，当孔的直径λ发生变化时，主要影响Warburg阻抗谱转折频率和中高频区的半无限扩散过程，在没有超出极限范围时，孔的直径λ对Warburg复阻抗所对应的低频极限电容的影响几乎可以忽略。

1) 中高频区，为高于转折频率且频率趋向增加的区域，即电荷半无限扩散区。一方面，当λ从0.1 μm增大到0.8 μm时，转折频率fk从未能显现，到在0.15 μm时显现为fk=0.16 Hz，然后单调增加到fk=4.0 Hz。fk从“无”到“有”预示储存于界面的电荷从不饱和区逐步过渡到饱和区，而fk随λ的增加而增加，表明孔直径增大有利于电荷离子的输运，加速电荷饱和区向高频方向扩展，加速半无限扩散区被“挤压”至高频区，因此，在下限频率fL=0.1 Hz固定的条件下，增加孔的直径λ时，Warburg阻抗谱观测结果为：电荷饱和区向高频区扩展，而半无限扩散区向高频区压缩，简言之，90°垂线变长，45°斜线变短。另一方面，当λ从0.1 μm增大到0.8 μm时，横跨45°Warburg区低频电阻RW从12.88 kΩ减小到0.41 kΩ，RW的急剧减小意味着电荷输运阻力的降低，这十分有利于储能器件最大功率密度的提高。

2) 中低频区，为低于转折频率且向频率下限趋近的区域，即电荷饱和区。当孔的直径λ从0.8 μm减小到0.15 μm时，在下限频率fL=0.1 Hz处，Warburg复阻抗虚部的绝对值从15.94kΩ增加至18.17 kΩ，对应的低频极限电容CL从100 μF降低到90 μF，孔的直径λ变化超过500%，而表征电荷储存容量的低频极限电容CL变化幅度为10%。当孔的直径缩小至0.1 μm时，电荷饱和区被严重压缩至几乎“不可见”，此时低频极限电容CL也将开始急剧减小。可见，在其他参数不变的条件下，增加孔的直径λ，对界面电容电荷存储容量的影响几乎可以忽略，但是显著增加了电荷输运速度，有利于提高储能器件最大输出功率密度。

如何从电化学动力学的角度来解释Warburg阻抗谱随孔的直径λ的演化规律，几乎完全类似于电解液单位长度电阻ri，因为孔的直径λ和电解液单位长度电阻ri这两个变量不独立，它们通过式(13)彼此关联。可以简单地理解为，ri对Warburg阻抗谱的影响，同λ-2的作用效果等价，因此，此处不再赘述。